一种小型无人机侦察吊舱目标定位方法*

黄 佳，崔乃刚

(1 中国工程物理研究院总体工程研究所，四川绵阳 621900；2 哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

目标定位是侦察型无人机的一项核心功能。文献[1-2]利用光学设备测量的角度信息与激光测距仪测得的距离信息通过几何关系求得目标相对无人机的位置参数。文献[3-4]在文献[1-2]的基础上，分别通过两点交会定位和三点交会定位进一步提高了定位精度。以上方法均要求无人机装配激光测距仪，然而对于小型无人机而言，侦察吊舱的体积与重量受到严格限制，加之成本的约束，使得装配激光测距仪不具有可行性。文献[5]给出了一种基于平坦地势假设的方法，即假设目标高度、无人机当前位置对应的地面高度、无人机起飞点高度三者相等，将无人机当前高度减去起飞点高度视为无人机相对地面高度，进而通过几何关系实现目标定位。该方法基于的平坦地势假设在实际工程应用中不具有普适性。文献[6]提出一种基于数字高程模型(DEM)的目标定位方法，但该方法需要装订目标所在区域的DEM，工程上同样不具有普适性。

为实现在不具备激光测距仪或其它测距设备条件下的目标定位，且在小型无人机上具有工程可实现性和普适性，文中提出一种新的目标定位方法。该方法基于速度与角速度的关系，仅利用无人机自身的导航信息和侦察吊舱测得的角度和角速度信息进行定位解算，不依赖于测距信息和DEM，也无需基于平坦地势假设，工程实现容易，仿真结果表明该方法具有一定的工程应用价值。

1 坐标系定义与转换

地心坐标系(Oexeyeze，简称地心系)，原点Oe位于地心，Oeze指向北极，Oexe在赤道面内指向格林尼治子午线，Oeye由右手定则确定。

无人机机体坐标系(Obxbybzb，简称体系)，原点Ob位于无人机质心，Obxb沿纵轴指向前，Obyb垂直于纵对称面指向右，Obzb在纵对称面内指向下，即“前右下”。

导航坐标系(Onxnynzn，简称导航系)，原点On位于无人机质心，Onxn在当地水平面内指向北，Onyn在当地水平面内指向东，Onzn垂直于当地水平面指向下，即“北东地”。

视线坐标系(Osxsyszs，简称视线系)，视线系与光学侦察吊舱固联，原点Os位于光学侦察吊舱旋转中心，Osxs沿镜头中心指向前，Osys垂直于镜头纵对称面指向右，Oszs在镜头纵对称面指向下，即“前右下”。

目标坐标系(Otxtytzt，简称目标系)，原点Ot位于目标几何中心，Otxt在当地水平面内指向北，Otyt在当地水平面内指向东，Otzt垂直于当地水平面指向下，即“北东地”。

导航系到体系的坐标转换矩阵为：

(1)

式中：ψ、θ、φ分别为无人机偏航角、俯仰角与滚转角，可由无人机导航系统给出。

体系到视线系的坐标转换矩阵为：

(2)

式中:α、β分别为侦察吊舱的高低角与方位角。

地心系到导航系的坐标转换矩阵为：

(3)

式中:B、λ分别为大地纬度与经度。

2 基于姿态/激光测距的目标定位方法

传统的基于姿态测量与激光测距的目标定位原理如下。

(4)

式中：下标e表示地心系，下标x、y、z表示分量的方向。

根据无人机的大地纬度B、经度λ以及大地高度h可求得无人机在地心系的坐标[7]，即：

(5)

式中:N为地球卯酉圈半径，e为地球第一偏心率。

进而可得，目标在地心系的坐标：

(6)

最后，目标的大地纬度Bt、经度Lt以及大地高度ht可由下式求出[7]：

(7)

式中:a、b、e、e′为地球长半轴、短半轴、第一偏心率、第二偏心率。

3 基于速度/角速度的目标定位方法

根据矢量在旋转坐标系中的导数关系[8],有

(8)

将式(8)分解到视线系，可得：

(9)

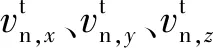
(10)

进而可得：

(11)

(12)

式(12)同样忽略了地球自转角速度。

4 定位精度仿真与分析

4.1 静止目标仿真与分析

对于静止目标，影响定位精度的误差源包括：无人机导航系统速度误差、姿态角误差、位置误差；吊舱的框架角误差、视线角速度误差。另外，误差源对定位误差的影响还与无人机和目标的相对运动关系有关，如相对距离、相对高度、相对速度。

文中以某小型无人机的6自由度仿真模型为例，设计无人机以200 m高度和35 m/s速度对目标进行盘旋跟踪。表1为几种典型仿真条件下的最大定位误差。

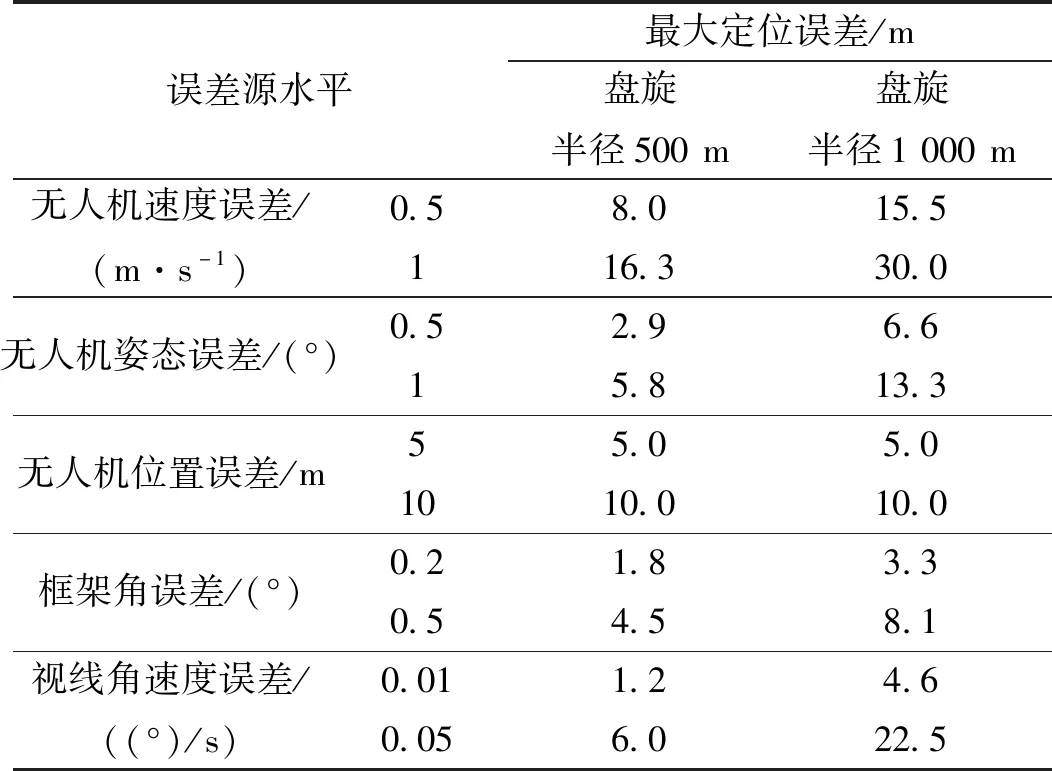
表1 几种典型仿真条件下的最大定位误差

由表1可见，几种典型误差源产生的定位误差在量值上基本相当；不同误差水平对定位误差的影响基本是线性的；无人机位置误差对定位误差的影响是平移关系，即多大的无人机位置误差就产生多大的定位误差，其余误差源对定位误差的影响均随盘旋半径的增大而增大。

根据表1中单项误差源对定位误差的影响，可由式(13)估算出多种误差源作用下的综合定位误差。

(13)

式中:σ为综合定位误差标准差；σi为单项误差源产生的定位误差标准差。

根据表1中的误差水平，由式(13)可求得综合定位误差为10.1～41.8 m，该定位误差可满足大部分小型无人机侦察任务的定位精度要求。

4.2 低速运动目标仿真与分析

由式(9)可知，文中的目标定位算法理论上需要已知目标的运动速度，而实际中目标的运动速度是难以获取的，因此文中的算法不适用于高速运动目标。对于低速运动目标(速度小于10 m/s)，这里将目标运动速度视为误差源，通过仿真分析目标运动速度对定位误差的影响。

仿真场景为：无人机以200 m高度、35 m/s速度绕目标以800 m半径盘旋跟踪；不考虑表1中的误差源，仅分析目标运动对定位误差的影响；目标分别以5 m/s和10 m/s做匀速直线运动，如图1和图2。

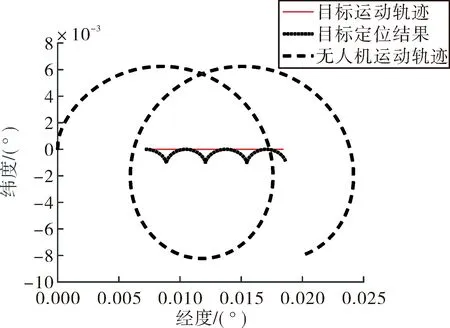
图1 目标5 m/s匀速直线运动的定位结果

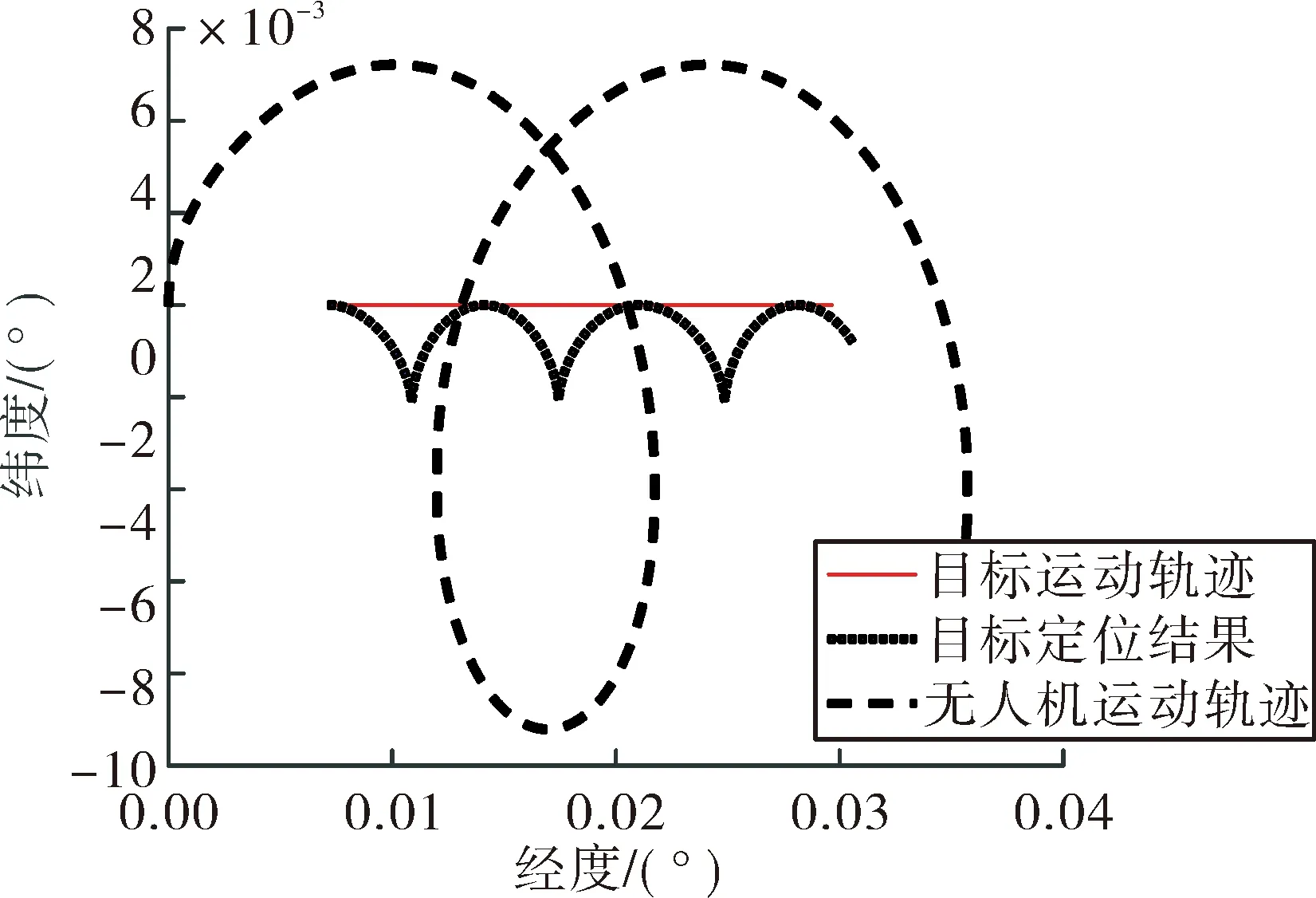
图2 目标10 m/s匀速直线运动的定位结果

由图1和图2可见，无人机和目标的相对运动关系直接影响到定位误差的大小。当无人机与目标的速度方向相互垂直时定位误差接近于0，因为此时目标速度在无人机运动方向上的分量为0。而当无人机与目标速度平行时定位误差最大，因为此时目标速度在无人机运动方向上的分量最大。图1和图2中最大定位误差分别为：104 m与209 m。该误差水平可满足对定位精度要求不高的侦察任务的指标要求。

5 结论

研究了一种仅利用无人机导航信息和光学侦察吊舱测量信息进行目标定位的新方法。该方法无需激光测距仪或其它测距设备的测距信息，无需基于平坦地面假设以及装订DEM，具有较高的工程可实现性和普适性。通过仿真设计了几种典型场景并分析了各项误差源对定位误差的影响。结果表明，在目标静止条件下，本方法具有较高的定位精度；对于运动目标，定位误差随目标运动速度增大而增大，且定位误差受无人机与目标的相对运动关系影响较大，当无人机与目标的速度方向相互垂直时定位误差接近于0，而当无人机与目标速度平行时定位误差最大。该方法可满足大部分小型无人机对静止目标的定位精度要求。对于10 m/s以内的低速运动目标，其定位精度同样可满足对定位精度要求不高的侦察任务的指标要求。