全程多约束条件下火箭弹最优轨迹设计及跟踪*

李佳星，温求遒，夏群利

(北京理工大学宇航学院，北京 100081)

0 引言

随着对远程精确打击火力的需求日益增加，提高火箭弹的射程和精确打击能力已经成为火箭弹研究的重要方向[1]。最优轨迹设计能够在多约束条件下，实现火箭弹射程的提高[2]。伪谱法是解决最优控制问题的最有效果的方法之一[3]。通过伪谱法得到最优弹道，再设计制导律实现最优轨迹的跟踪，使火箭弹能够在复杂环境下进行远程精确打击，已有学者在相关技术方面进行了研究。汤善同等针对远程防空导弹，研究了中制导段的弹道优化及制导问题[4]；夏红伟等研究了飞行器再入段的弹道优化与伪谱法的反馈制导方法[5]；张大元等针对防空导弹弹道跟踪问题，基于线性二次型调节器(LQR)理论设计了弹道跟踪制导律[6]。

文中针对火箭弹，以射程最远为性能指标，在全程多约束条件下进行了最优轨迹设计，然后基于线性二次型调节器设计跟踪制导律，实现了最优轨迹的多变量跟踪，最后通过仿真进行了验证。

1 制导火箭弹运动模型的建立

文中的研究对象为一种正常式布局的火箭弹，其飞行过程分为主动段和被动段，工作及控制过程如下：在接收到点火指令后，火箭发动机工作，火箭弹以固定的射角发射，进入到具有发动机推力作用的主动段。火箭发动机工作结束后，火箭弹进入被动段，做无动力飞行，在制导控制系统作用下，制导指令转换为舵指令，通过舵片偏转使火箭弹命中目标。为研究方便，假设地球表面为平面，不考虑地球自转，将舵片偏转的作用等效成攻角，建立火箭弹纵向运动方程组：

(1)

式中：V为火箭弹飞行速度，θ为弹道倾角，x为射程，y为高度，P为发动机推力，α为飞行攻角，D、L分别为空气阻力和升力，其计算方法为D=cxρV2s/2，L=cyρV2s/2，s为弹体特征面积，ρ为大气密度，其数值可通过参考文献[7]获得。cx和cy为阻力系数和升力系数，它们是攻角和马赫数的函数，可以通过下式计算得到：

(2)

式中：f(Ma，α)和g(Ma，α)是自变量为马赫数和攻角的拟合函数。

2 优化模型的建立及求解

2.1 优化模型的建立

为了求解最优控制问题，应先建立优化模型[8]。

1)状态方程：即为式(1)，其中V、θ、x和y为状态变量，攻角α为控制变量。

2)初始条件：V=V0、θ=θ0、x=x0及y=y0

3)边界条件：需满足下列边界条件：

(3)

4)控制约束：αmin≤α≤αmax

5)终端约束：V=Vf、θ=θf、x=xf及y=yf

6)性能指标函数：

(4)

式中：x(t)∈Rn为状态变量，u(t)∈Rm为控制变量，t0为初始时间，tf为终端时间，Φ(x)为Mayer型代价函数；g(x)为Lagrange型代价函数。

2.2 优化问题求解

将优化问题看成最优控制问题，并寻找控制变量，使得具有一般性的Bolza型性能指标函数即式(4)最小，并满足以下约束：

1)系统动力学微分方程约束

(5)

2)终端边界约束

φ(x(t0)，x(tf)，t0，tf)=0

(6)

3)不等式路径约束

C(x(t)，u(t)，t)≤0

(7)

对最优控制问题采用伪谱法将Bolza型问题转化为非线性规划问题。首先将全程时间区间[t0，tf]划分为K个网格子区间[tk-1，tk]，k=1，…，K。将每个网格子区间的时域t∈[tk-1，tk]转变为τ∈[-1，+1]，即：

(8)

然后将每个网格子区间[tk-1，tk]内的状态变量和控制变量离散化，并构建多项式来逼近状态变量和控制变量，得到近似方程式：

状态变量x(k)(τ)可近似为：

(9)

控制变量u(k)(τ)可以近似为：

(10)

式中：Nk为区间[tk-1，tk]内的配点数，Li(τ)及Lj(τ)Lagrange插值多项式，即：

对近似状态方程式(9)求微分，将Nk个配点上的动力学微分方程约束变为代数方程约束，即：

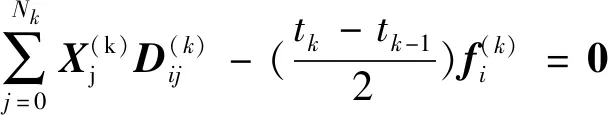
(12)

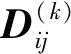
每个子区间内的Nk个配点上的路径不等式约束为：

(13)

式中，i=1，…，Nk；k=1，…，K。

边界条件为：

(14)

将Bolza型性能指标函数式(4)中的积分项近似为：

(15)

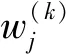
(16)

通过上述方法，求得每段配点处的状态变量和控制变量，在满足各种约束的情况下使得性能目标函数最小。这种非线性规划问题能够通过序列二次规划算法(SQP)进行求解。

3 基于LQR的跟踪制导律设计

上一节研究了火箭弹最优轨迹设计方法，求得了全程多约束条件下的最优弹道。但是火箭弹在飞行过程中受多种偏差影响，文中采用线性二次型调节控制方法，设计闭环制导律对最优弹道进行跟踪，首先要将运动学方程线性化。

3.1 线性化模型

小扰动假设条件下，以时间为自变量，选取y、V和θ作为反馈跟踪量进行设计，即：

(17)

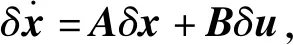
(18)

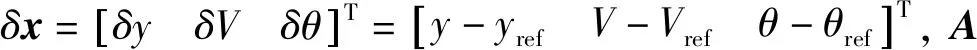
其中，Dy、DV、Ly、LV、Dα、Lα分别为阻力、升力加速度的偏导数，有：

其中气动力系数导数由以下计算方法得到，即：

3.2 基于LQR的跟踪制导律

(19)

式中：Q和R为状态向量和控制向量的加权矩阵。为了让性能指标J的值最小，控制量应符合[9]：

u*(t)=-R-1(t)BT(t)P(t)x(t)=-K(t)x(t)

(20)

则：

δu=δα=-R-1BTPδx(t)=-Kδx

(21)

式中：P是Riccati方程PA+ATP-PBR-1BTP+Q=0的解，K=(K1，K2，K3)为增益向量。进一步求得实际控制量：

αc=αref+δα=αref-K1δy-K2δV-K3δθ

(22)

式中αref为最优轨迹的攻角指令。

在最优弹道上选取多个特征点，分别求得反馈增益参数，预先装订成反馈增益向量。对于火箭弹，在飞行全过程中可根据实时的动压,通过插值得到反馈增益系数。

4 仿真分析

4.1 火箭弹弹道优化

文中研究的火箭弹飞行任务，为了使火箭弹具有较大的射程，故以射程作为最优指标，该弹道优化问题可表述为：

1)状态方程：即为式(1)。火箭发动机在0～25 s内工作，P=39 kN，假设质量均匀变化。特征面积s=0.282 6 m2，气动力系数如下列拟合函数计算：

2)初始条件：V=20 m/s、θ为待优化量，范围[20°，80°]、x=0和y=0。

3)边界条件：需满足下列条件：

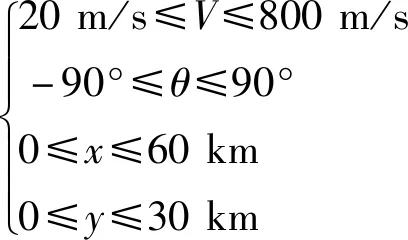
4)控制约束：-18°≤α≤18°

5)终端约束：θ=-70°、y=0和|αt|≤3°。

6)性能指标函数：J=-xtf

仿真结果如图1和图2所示。

图1 优化前后弹道对比图

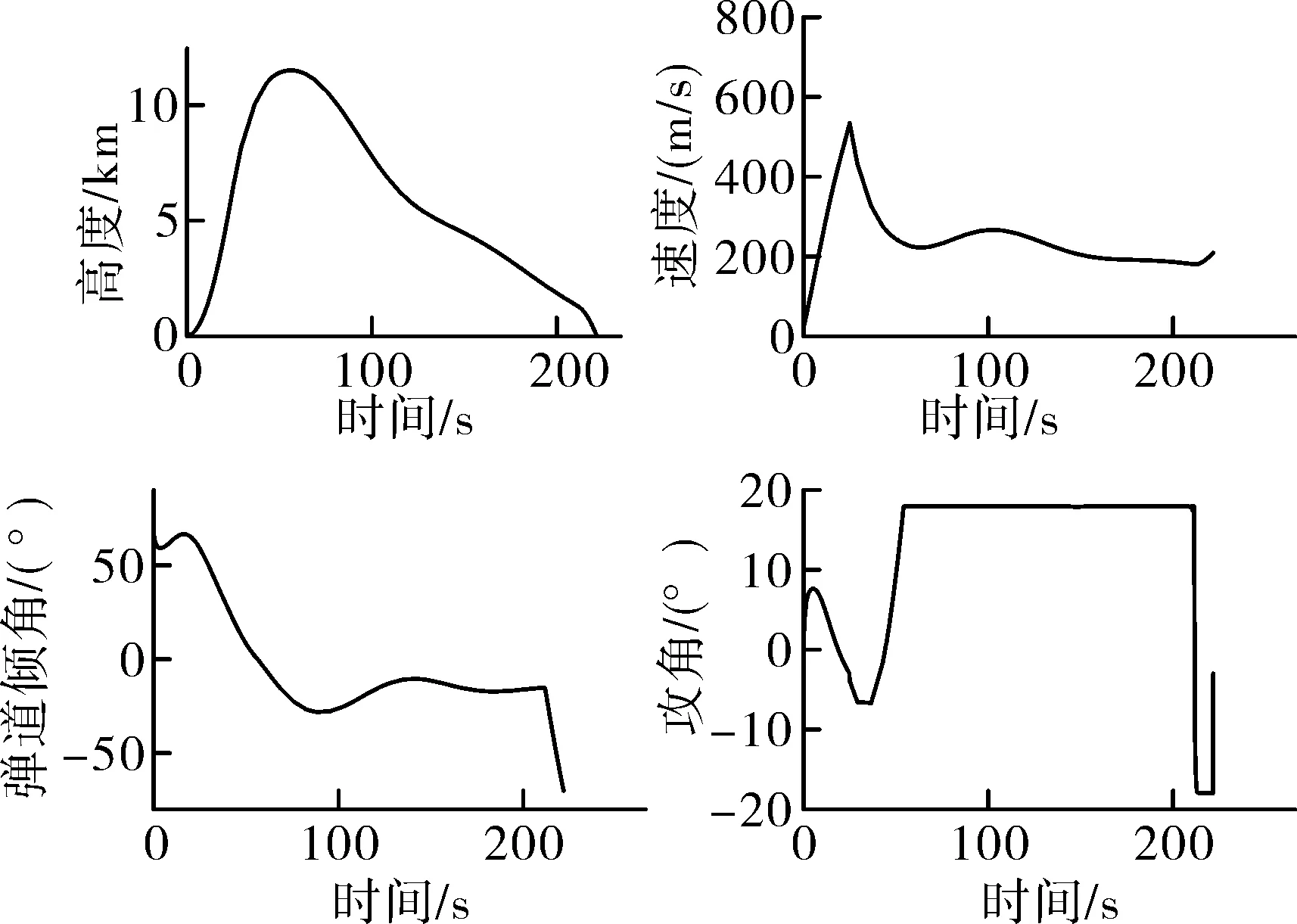
图2 最优轨迹对应状态量变化曲线

由仿真结果可得：优化方案达到了增大射程的目的，火箭弹在大部分时间保持正极限攻角飞行，最终射程为45.26 km，末端攻角为-2.99°。

4.2 火箭弹跟踪制导

选取制导律权重系数矩阵为：Q=diag(1，1，1)，R=1。

仿真中，加入拉偏项，即密度+5%，阻力系数+5%，升力系数+5%，并加入开环制导作为对比，即将αref直接作为制导指令，仿真结果如图3～图6所示。

以上结果表明：开环制导虽然能使跟踪弹道的攻角指令与最优弹道保持一致，但是在存在微小扰动的情况下，跟踪弹道的高度、速度和弹道倾角已经产生明显偏差，其中跟踪高度已经偏离最优弹道超过200 m，而LQR跟踪制导实现了对最优弹道的跟踪和逼近，高度、速度、攻角和弹道倾角等与最优弹道十分接近，基本实现了多变量的跟踪。

图3 弹道曲线

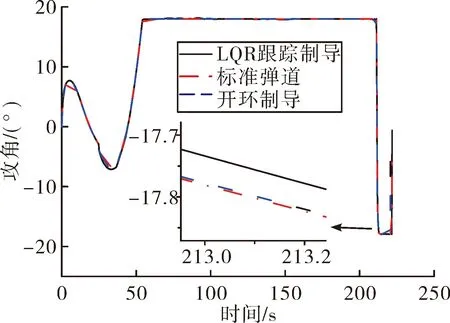
图4 攻角曲线

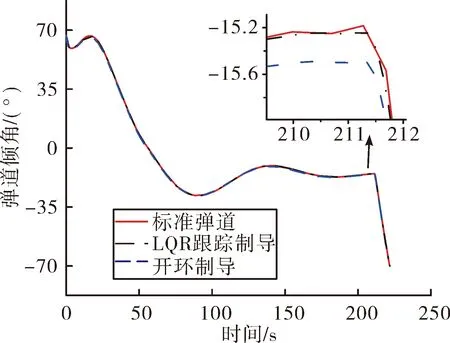
图5 弹道倾角曲线

图6 速度曲线

5 结论

对火箭弹进行了最优轨迹设计与跟踪制导方法的研究，根据任务特点设定射程最大为优化目标，并采用伪谱法得到满足全程多约束的最优弹道。将火箭弹运动方程关于最优弹道线性化后，基于LQR设计了跟踪制导律，实现了多变量的跟踪。并通过仿真验证了该制导方法的可行性和优越性。