基于UWB/PDR的组合室内定位算法*

陈隆亮，杨 昳，袁 恩，赵跃新，张 超

(1.陆军工程大学，江苏 南京 210007；2.解放军78111部队，四川 成都 610014；3.成都工业职业技术学院，四川 成都 610218)

0 引言

全球卫星导航系统(北斗、GPS、GLONASS等)的定位精度不断提高，丰富了室外基于位置信息的服务，方便了人们的生活。相比室外环境，室内细粒度的环境为多样化的位置信息服务提供了更多可能。但是在室内环境中，由于遮挡，基于卫星信号的定位系统精度严重恶化，甚至无法定位，严重阻碍了位置服务、行人导航的发展[1]。因此，人们对室内定位技术的需求日益增加。近年来，各种室内定位方法层出不穷，但是精度普遍不高，用户体验不佳，普适的高精度的室内定位依然是目前研究的热点。

目前，常见的室内定位技术主要有：基于射频信号的定位技术，包括红外线、超声波、蓝牙、超宽带、WiFi等[2-6]；基于惯性传感器的定位技术，包括行人航迹推算、地磁匹配等。基于射频信号的定位技术具有使用方便、定位精度高等优势，但存在非视距、多路径效应的情况[7]。基于行人航迹推算的定位技术具有自主性和连续性的优势，但随着时间的推移存在累积误差缺陷[8]。因此，联合上述两种定位方法，发挥各自的技术优势，是实现高精度、高可靠的室内定位的可行途径之一。

本文提出基于UWB/PDR的信息融合算法，将UWB定位系统和PDR定位系统组合，互相补充，构成一种稳定、精度更高的组合定位系统。目前，在卫星导航和惯性导航融合领域，已有大量的算法研究，而针对室内组合定位系统融合算法的相关研究较少，主要的方法是卡尔曼滤波[9]。但是在室内组合定位系统中，其状态方程和观测方程都为非线性方程，传统的卡尔曼滤波并不适用。扩展卡尔曼滤波可以将上述方程线性化，但是其近似误差降低了模型的准确性，随着时间的累计，其估计精度难以保证[10]。无迹卡尔曼滤波采用无损变换，无需对非线性状态函数和观测函数求导，收敛速度快，估计精度高，但是由于计算误差和噪声引起的误差协方差矩阵为负定会导致滤波发散[11]。同时，传统的组合定位方法并未考虑复杂室内环境中存在非视距的特殊情况，其在实际应用中可能出现定位误差的剧烈抖动和滤波发散的情况。本文采用误差状态量卡尔曼滤波，将每个系统的真实值对消，其残差的状态和观测方程均为线性方程，因此没有近似误差，提高了融合后的定位精度，同时加入了非视距检测模块，增加了系统的鲁棒性，提高了定位精度。

1 UWB定位

因为信号的时域分辨率和信号的带宽具有倒数关系，所以UWB系统的时域分辨率能够达到纳秒级别，因此，其能够在时域上分辨通过室内多条路径在不同时间到达天线的信号[7]。在锚节点和待定位节点时间同步的情况下，UWB系统便能准确测量信号的传播时间，如果信号传播存在直达路径，那么采用基于到达时间的定位算法[12]就可以计算出待定位节点的位置。假设二维平面中，UWB锚节点个数为N，待定位节点发送信号的时刻为T，第n个锚节点接收到信号的时刻为Tn，那么第n个锚节点的空间位置和其接收信号的时刻存在如下关系：

(1)

其中，c为光速，(xn,yn)为锚节点的二维坐标。联合N个锚节点的方程，便可以求解出待定位节点的坐标(x,y)。从式(1)可以看出，待定位节点和锚节点之间的时间同步直接影响了定位精度，实际中，基于到达时间的UWB定位系统由于时间同步存在误差，定位精度下降较大。

2 PDR定位

在室内环境中，大多数人员携带的待定位节点都是小型设备，这些设备上的惯性器件由于成本、功耗、体积等因素，性能较差，远远不能满足基于积分方法的惯性导航[13]。但是，由于人员走动的特殊性也带来了新的航迹推算方法：由于人的行走具有周期性，因此可以利用加速度计的周期起伏判断人的行走步数，通过地磁或者电子罗盘判断人的行走方向，通过步长模型(如步频-步长模型)判断人的行走步长。联合步数、方向、步长，便可以实现行人的航迹推算。如果已知出发点的位置为(x0,y0)，用户移动方向与地理正北方向夹角为θ，那么用户到达的位置(xn,yn)可以由下式计算：

(2)

其中，n为步数，θi、li分别为第i步的方向和步长。

3 UWB/PDR融合定位算法

本文提出的UWB/PDR融合定位算法的总原理框图如图1所示。

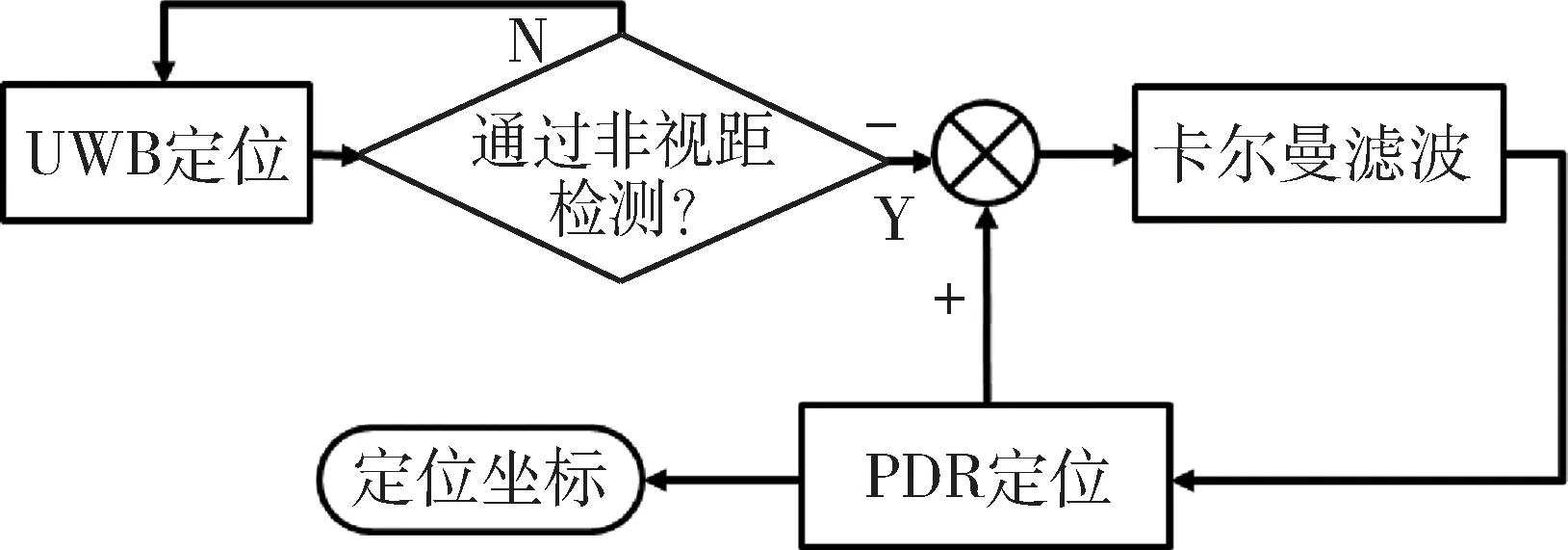
图1 UWB/PDR融合定位原理框图

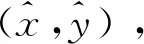
3.1 非视距检测

当存在非视距时，由于折射、反射的影响，UWB测量得到的信号到达时间大于信号直线传播情况下的时间，在这种情况下，UWB系统的定位误差将增大。当进行卡尔曼滤波时，由于方程的误差不是随机噪声造成的，滤波可能出现发散现象。因此本文提出了非视距检测，在滤波前过滤掉被非视距污染的UWB定位数据，增加系统的稳定性，提高融合精度。

由于UWB定位系统可以以较高的位置更新率进行工作，同时行人的步行速度有限，在UWB两次测量的间隔时间(50 ms)内，移动的距离很小，因此UWB的测量值不会存在突变现象。基于上述假定，如果满足如下条件，本文则认为存在非视距情况：

min(αn,αn+1,αn+2)>φ

(3)

假定系统应用的实际环境中，非视距仅仅是临时由于墙、柱子、管道等的遮挡造成的，如地下停车场、工厂房等环境，而不考虑长期的非视距情况，在该情况下，可以多布设UWB节点满足需求。因此，在非视距区域，行人移动的距离并不大。基于上述假定，如果满足如下条件，则认为离开非视距区域：

max(βn,βn+1,βn+2)<φ

(4)

3.2 卡尔曼滤波

在排除了非视距引起的误差后，假设其余误差都由白噪声引起。本文采用残差状态量作为UWB/PDR滤波的输入，其优点是系统的状态方程和观测方程都为线性方程，因此可以采用线性卡尔曼滤波将UWB和PDR输出的信息进行融合，避免了非线性带来的复杂性。考虑二维平面情况，定义k时刻的残差状态变量为4维向量：

xk=[δNk,δEk,ξLk,ξdk]T

(5)

式中，δNk、δEk、ξLk、ξdk分别为k时刻北向、东向的位置误差，步长检测器和陀螺仪的一阶马尔科夫过程漂移。那么根据PDR原理，该系统的状态方程为：

xk=Axk-1+Fwk-1

(6)

(7)

那么观测向量为zk=[zn,ze]T。观测方程为：

zk=Hxk+vk

(8)

4 仿真结果分析

在本文的仿真中，假设行人以每秒2步的步频、0.7 m的步长匀速行走，UWB定位系统每秒输出20次定位结果，以UWB时间为准将PDR数据对准。利用卡尔曼滤波进行数据融合。PDR系统行走方向噪声方差为(0.7°/步)2，步长噪声方差为(0.07 m/步)2，UWB系统定位误差由方差为(1 m)2的白噪声引起。PDR系统、UWB系统及组合后的系统在东向和北向上的定位误差仿真曲线如图2、图3所示。

图中虚线为UWB系统定位误差，点线为PDR系统定位误差，粗实线为组合系统的定位误差，从图中可以看出，PDR系统随着步数的增加，其累计误差效应明显，UWB系统误差存在较大的抖动。UWB/PDR组合室内定位系统既可有效抑制PDR系统的误差随时间发散的问题，同时也明显减小了UWB定位误差的抖动。

图4展示了不同方法的累计误差分布，从图中可以看到，总体上，组合后的系统在一定程度上提高了定位精度，其定位误差90%在1 m以内，为行

图2 UWB、PDR和Kalman组合系统的东向误差曲线图

图3 UWB、PDR和Kalman组合系统的北向误差曲线图

图4 UWB、PDR和Kalman组合系统的仿真累计误差分布图

人室内导航提供了可靠基础定位数据。

5 实验结果及分析

为了验证本文提出的UWB/PDR组合室内定位方法在实际中存在非视距情况下的有效性和鲁棒性，选取DW1000型号的UWB节点和三星Galaxy S9型号的移动智能终端作为硬件平台进行算法实际测试。UWB定位系统定位更新频率为20 Hz，基于安卓系统开发的PDR系统中，惯性传感器数据采样频率为50 Hz，以UWB信号采集时间戳为基准，对齐实时步态检测的定位位置。实验场地如图5所示，中间为封闭天井的环形走廊，大小为11.18 m×11.70 m。其中，天线标志为UWB节点位置。以UWB初始定位位置为PDR系统初始位置，实验者手持设备沿预定轨迹匀速行走一圈。实验结果如图5所示。黑色实线为真实轨迹，虚线和点线分别为UWB定位和PDR系统定位轨迹，带五角星的轨迹为卡尔曼滤波融合轨迹。

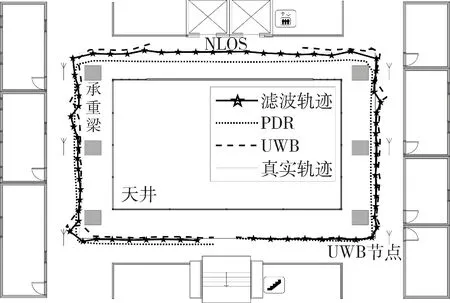
图5 UWB、PDR和Kalman组合系统的定位结果

对比真实的行走轨迹、PDR定位轨迹、UWB定位轨迹和UWB/PDR组合定位轨迹可以发现，UWB/ PDR组合定位算法能有效修正单独采用PDR系统定位产生的积累误差，并减轻了UWB系统定位抖动的缺点，更接近真实行走路径。

同时，在测试中，当实验者行走至图中电梯口处，由于UWB信号被承重梁遮挡，出现了非视距现象，已经无法接收到3个以上的UWB信号进行定位，单纯的UWB定位系统出现了轨迹丢失问题，而在该区域，PDR系统则表现良好。图6对比了传统卡尔曼滤波和本文提出的带非视距检测的卡尔曼滤波的误差分布。可以看到，由于非视距的影响，传统的卡尔曼滤波出现了很大的误差，而本文的算法由于检测到了非视距的存在，消除了非视距的影响，大大降低了整个定位系统的误差，提升了系统的定位精度。

图6 NLOS检测Kalman和传统Kalman的实测累计误差分布对比图

6 结论

为了提高在复杂室内环境中的定位效果，本文提出了一种带非视距检测的UWB/PDR组合室内定位算法，组合定位算法既克服了超宽带系统在非视距情况下的定位精度抖动问题，又避免了行人航迹推算的累计误差。均匀步长行走的实际测试表明，组合算法提升了定位的精度和稳定性，在复杂的非视距环境中能够稳定工作，具有很强的实用性。下一步工作将研究如何将定位结果反馈回UWB系统，用以对每一步步长进行精确校正，解决在非均匀步长行走时带来的步长误差问题，实现更加鲁棒的定位系统。