基于共轭梯度法迭代优化的图像分类算法

杨子琳， 朱志斌， 马金瑶

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

近年来，基于深度学习的图像分类受到越来越多人的关注，其典型模型是深度卷积网络。深度卷积网络主要由卷积层、池化层以及全连接层构成，通过一系列的卷积层与池化层将提取的图像特征进行压缩[11]，从而结合分类器，实现图像的分类。

假设对于k分类，具有m个训练样本为{(x(1),y(1)),…,(x(m),y(m)),y(i)∈(1,2,…,k)}。深度卷积网络最常用softmax作为分类器，该分类器是根据输入x,估算出每个类别j的概率值P(y=j|x)。其中，softmax函数表达式为

(1)

其中：hθ(x(i))的每个元素P(y=j|x;θ)表示样本x(i)属于类别j的概率；θ为模型参数向量。

确定分类器的输出后，图像分类任务的目的是最小化模型代价函数：

(2)

其中，1condition表示condition为真时，其值为1，否则为0。因此，图像分类的神经网络训练问题转化为通过优化问题求解模型的最优参数的问题。用于深度学习中的优化算法主要有一阶算法和二阶近似算法。一阶算法有固定学习率算法，如随机梯度算法；自适应学习率算法，如AdaGrad算法[10]。二阶近似算法如共轭梯度算法。

共轭梯度算法求解问题(2)的常用迭代公式为

xk+1=xk+αkdk；

(3)

(4)

其中：gk为目标函数梯度；dk为搜索方向；αk为步长，αk≥0；βk为迭代更新参数。通过改变参数βk，可得到不同的共轭梯度算法。著名的βk公式有FR、PRP、HS、DY等[4,7]。当目标函数保持严格凸性以及搜索时采用精确搜索，这几个公式是一样的，但当目标函数为一般函数时，它们存在显著区别。对于全局收敛性，FR、DY公式表现良好[6,8]；数值效果上，HS、PRP公式占优势，但HS、PRP公式不一定收敛[1-3,9]。

1 一种修正的HS共轭梯度算法

受文献[3，8]的启发，通过改变参数θk、βk，提出了一种修正的HS共轭梯度算法：

(5)

(6)

其中，1≤μ≤2，yk-1=gk-gk-1。

对于任一线搜索，有

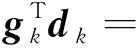
显然，该算法的搜索方向均具有充分下降性。

算法步骤为：

1)初始化x0∈Rn,ε>0，ρ∈(0,0.5),σ∈(ρ,1),μ∈(1,2),k=1。

2)若‖gk‖≤ε，则停止；否则，转步骤3)。

3)由Wolfe准则计算步长因子αk：

(7)

(8)

4)令xk+1=xk+αkdk。

5)令k=k+1，转步骤2)。

2 全局收敛性分析

为确保问题(1)的局收敛性，作假设H：

1)f(x)在水平Ω={x∈Rn|f(x)≤f(x1)}有界；

2)f(x)在水平集Ω内连续可微，且满足Lispchitz条件，则存在常数L>0，使得

‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈Ω。

(9)

由假设H知，存在一个常数m>0，使得

‖g(x)‖≤m, ∀x∈Ω。

(10)

引理1[2]若假设H成立，则算法是良定的。

由(7)可知，目标函数数值序列{f(xk)}是一下降序列，故有

结合式(10)得

(11)

在证明算法全局收敛性之前，首先给出新的搜索方向下Wolfe搜索下的Zoutendijk条件。

引理2[3]若f(x)满足假设H，αk由式(7)、(8)确定，则有

(12)

(13)

由式(9)得：

又由式(8)得：

所以，

(14)

结合式(7)、(8)得：

f(xk+αkdk)-f(xk)≤

两边同乘-1，并结合式(14)可得：

f(xk)-f(xk+αkdk)≥ραk‖gk‖2=

两边累加可得：

因f(x)在水平集Ω={x∈Rn|f(x)≤f(x1)}有界，故结论成立。

在此基础上，进一步分析新算法的全局收敛性。

定理1若f(x)满足假设H，xk由式(3)确定，αk由式(7)、(8)确定，dk由式(5)确定，则有

(15)

证明由式(5)中搜索方向dk的定义及式(9)、(10)、(14)可得：

‖dk‖≤‖gk‖+2μ‖gk-1‖2×

由式(11)可知，存在常数ρ∈(0,1)和正整数k，使得当k≥k0时，有

因此，对任意k>k0，有

‖dk‖≤m+ρ‖dk-1‖≤m+ρ(m+ρ‖dk-2‖)≤

m(1+ρ+…+ρk-k0-1)+ρk-k0‖dk0‖≤

3 数值实验

为了验证本算法在图像分类任务中能够较快地得到模型的最优参数，从而提升分类速度和分类准确率，对本算法进行数值实验。其中，误差ε=10-5，μ=1.8。

1)针对文献[3]中的问题进行相关测试。本算法对不同维度的问题进行了相关测试，并与文献[3]测试结果进行对比，结果如表1所示。

表1 本算法与文献[3]算法的测试结果

2)将本算法应用于神经网络中。本实验构造了一个简单的二分类逻辑回归网络，用于识别猫。其中，训练集为209张64×64×3的带标签图片，测试集为50张64×64×3的带标签图片，标签为“1”表示猫，标签为“0”表示不是猫。将本算法与神经网络中常用的随机梯度算法进行对比，测试结果如表2所示，本算法在网络中的成本损失如图1所示。

表2 本算法与随机梯度算法的测试结果

图1 本算法在每10次迭代下的成本损失

从表1可看出，本算法在迭代次数较少及在维数较多情况下均能以较短的时间中求解到最优解。从表2可看出，在逻辑回归网络中，本算法比随机梯度法具有较少的迭代次数，测试集准确率有所提升。从图1可看出，损失值随迭代次数变化，最终趋向于一个较小的值。实验结果进一步表明了算法的有效性。

4 结束语

基于传统的HS方法，引入一个谱参数θk，通过对参数θk、βk的修改，提出了一种修正的HS共轭梯度算法。在Wolfe搜索下，证明了该算法具有全局收敛性，并通过实验测试，进一步验证了算法的有效性。