不忘初心——离心率，相似椭圆——斜率积

☉潍坊新纪元学校 高继勇

☉潍坊新纪元学校 刘 丹

在一些建筑、景观等结构的视图中，经常会碰到两个及两个以上中心与对称轴相同、离心率相等的椭圆问题，我们往往称此类两个及两个以上的椭圆相似.涉及两个相似椭圆，有很多优美的平面直观以及几何性质.下面结合两个相似椭圆中对应两切线的斜率之积与对应椭圆的离心率之间的关系加以实例剖析，并进一步拓展延伸、规律总结.

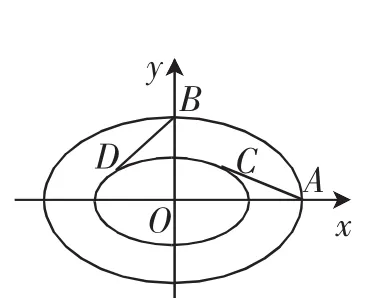
图1

一、问题呈现

问题如图1所示，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC，BD，设内层椭圆方程为（a＞b＞0），若直线AC与BD的斜率之积为-，则椭圆的离心率为______.

从两个相似椭圆的外层椭圆顶点（一个长轴顶点与一个短轴顶点）向内层椭圆引两条切线，进而通过两切线的斜率之积所对应的值来探求椭圆的离心率.从运动的角度来看，可以固定一层椭圆，让另一层椭圆运动，随着该层椭圆的运动，切线的位置也适当地发生了改变，由此可以确定这两条切线的斜率之积必须是定值，从而说明这两条切线的斜率之积与椭圆的离心率之间存在对应关系，但与椭圆的大小无关.

二、多解剖析

解法1：设外层椭圆方程为0，m＞1），则A（ma，0），B（0，mb）.

联立2ma3k12x+m2a4k12-a2b2=0.

因为Δ1=（-2ma3k12）2-4（b2+a2k12）（m2a4k12-a2b2）=0，

解法2：设外层椭圆方程为0，m＞1），则A（ma，0），B（0，mb）.

解法3：从特殊位置入手，通过固定内层椭圆，让外层椭圆运动，使切线AC恰好经过点B，根据椭圆的对称性可知此时直线AC与直线BD关于y轴对称.

点评：由于在相似椭圆中，两切线的斜率之积与椭圆的离心率之间存在着对应关系，这就为利用特殊位置法提供了条件，此类方法在解决本题时可以简化过程，真正做到“小题小做，小题巧做”的目的.通性通法——直线与椭圆的位置关系法是解决此类问题最常见的基本方法，也是解决此类问题的基本思维方式，而切线性质法与参数坐标法是在通性通法的基础上的进一步拓展.特别是在以上的破解过程中，也为进一步的拓展提升以及规律总结提供了条件.

三、拓展提升

根据以上对应的问题，交换相应的条件与结论，可得到以下相应的变式：

变式1：如图1所示，设内层椭圆方程为b＞0），内外两个椭圆的离心率均为从外层椭圆顶点向内层椭圆引切线AC，BD，则直线AC与BD的斜率之积为______.

解析：从特殊位置入手，通过固定内层椭圆，让外层椭圆运动，使切线AC恰好经过点B，根据椭圆的对称性可知此时直线AC与直线BD关于y轴对称.

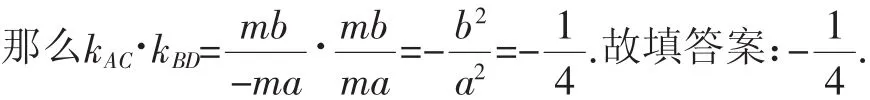
点评：通过对原问题进行变式，将原问题的条件与结论变为新问题的结论与条件，可以得到进一步的拓展与提升，也为进一步的规律总结指明方向.

四、规律总结

根据以上对应的问题以及相应的多解剖析可得到一般性的结论：

结论1：如图1所示，设内层椭圆方程为b＞0），内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC，BD，若直线AC与BD的斜率之积为-λ（0＜λ＜1），则椭圆的离心率

具体的证明过程可以参照以上的多解剖析的思维过程.进一步总结规律，并结合变式1中的问题即可得到相应的一般性的结论：

结论2：如图1所示，设内层椭圆方程为b＞0），内外两个椭圆的离心率e相同，从外层椭圆顶点向内层椭圆引切线AC，BD，则直线AC与BD的斜率之积为e2-1.

具体的证明过程可以参照以上变式1的解析过程，这里则不加以叙述.

其实，在探索圆锥曲线中的求解问题时，往往可以发现点、直线、圆、圆锥曲线以及其相互之间的内在联系与规律，从而加强对其相关内容的正确理解与掌握，真正达到“小题小做，小题巧做”的目的，有助于数学解题能力与应用能力的提高，真正达到提升综合能力，拓展数学素养的目的.