基于机器人柔性毛刷的空间翻滚目标消旋

吴昊，孙晟昕，魏承,*，张海博，赵阳

1. 哈尔滨工业大学 航天学院，哈尔滨 150001 2. 北京控制工程研究所，北京 100000

随着航天技术的发展，人类的航天任务逐渐增多，由此产生的失效卫星、火箭末级、碰撞残留物等空间碎片对航天事业的发展产生巨大威胁[1]。为控制空间碎片数目增长，消除其对航天活动的威胁，空间碎片主动移除技术成为当前的研究热点[2]。

空间碎片多为非合作目标，长期处于失控状态，在复杂的空间环境影响下，最终会呈现自由翻滚运动。针对高速翻滚非合作目标的捕获策略即对目标施加阻力，进行消旋，降低其转动角速度，然后进行捕获[3]。

在接触式消旋方面，Daneshjou和Alibakhshi[4]提出一种弹簧阻尼器缓冲装置，通过喷管对接过程中的接触碰撞进行一定的消旋；Nishida和Kawamoto[5]设计了一种末端执行器为减速刷的消旋装置，利用减速刷与目标之间的弹性接触力进行消旋，减小后续抓捕冲击；Huang等[6-7]提出一种基于绳系终端的非合作目标姿态控制方法，利用黏性绳系附着到翻滚目标上，通过控制系绳拉力和阻尼力使其姿态稳定；Matunaga等[8]将弹性小球作为末端执行器，Yoshikawa和Yamada[9]利用多次接触碰撞所产生的脉冲作用力来衰减目标的章动角和自旋转速，抑制非合作目标卫星的角动量。另有增阻装置等空间碎片清除系统，通过增大目标的面质比，从而增大空气阻力，以加速目标的消旋过程，方法包括向空间碎片喷射泡沫[10-11]和为空间碎片安装气囊[12]等；激光推移是利用激光束照射空间碎片表面，使辐照区材料产生热物质射流并向外喷出，从而产生反向作用力而改变碎片轨道[13-16]。

针对消旋过程中消旋机构的稳定问题，通过采用滑模控制来实现机械臂的快速响应及稳定性。在滑模控制方面，童超[17]设计了一种基于模糊幂次趋近律的快速滑模控制方法，来解决空间机器人轨迹跟踪控制过程中的收敛速度及抖振抑制问题，其收敛速度优于传统滑模面，达到了很好的效果。谢立敏和陈力[18]讨论了漂浮基柔性关节-柔性臂空间机器人系统的运动控制律设计，采用非线性滑模控制方法实现空间机器人期望运动轨迹的渐近跟踪。Kawamura等[19]利用Lyapunov稳定性定理，提出了一种基于干扰观测器的滑模控制设计方法，降低了滑模控制器中切换项的增益，有效地消除了抖振。Mobayen等[20]针对一类具有不匹配非线性不确定系统的跟踪问题，研究了一种基于线性矩阵不等式的二阶快速终端滑模控制技术，对控制性能和跟踪性能都有明显的改善。Oliveira等[21]提出了一种基于扩展等效控制概念的自适应滑模方法来处理非线性系统中未知界的干扰，以避免对控制器增益的过度估计和滑动运动的损失。Yang等[22]设计了一种新的非线性扰动观测器用于风力发电系统的鲁棒滑模控制，其中采用双馈感应发电机实现了具有改进的故障穿越能力的最优功率提取。

消旋作为一个崭新的研究课题，在国内外仍旧停留在理论阶段。翻滚非合作目标的姿态及速度辨识、消旋过程的接触碰撞动力学分析、消旋装置的机构设计、防碰撞抑振设计、机械臂柔顺控制方法等都是值得研究的方向。

1 消旋动力学

本文设计了一种末端为柔性减速刷的空间机器人，对空间翻滚目标进行消旋。该消旋机构具有柔性，针对处于自由翻滚状态的非合作目标，具有软接触的特性，能够提高消旋的安全性。模型如图1所示。

定义坐标系和符号：坐标系ΣI为惯性坐标系；坐标系Σb为基体本体坐标系；坐标系Σt为目标本体坐标系；q=[q1,q2,q3,q4,q5,q6,q7]为机械臂各关节变量；qb=[qb1,qb2,qb3]为基体的姿态欧拉角；Ci为机械臂第i根杆的质心；Ji是连接第i-1和i根连杆的关节；Iri为机械臂第i根杆的质心在惯性坐标系下的位置向量；Ir0是基座航天器质心在惯性坐标系下的位置向量；Irg为空间机器人系统质心位置向量；Iωi为机械臂第i根

图1 七自由度机械臂模型Fig.1 A model of seven-degree-of-freedom manipulator

连杆的角速度；Iω0为基座的角速度；Iωt为目标的角速度；mi为空间机器人第i根连杆的质量。左上角I表示向量在惯性坐标系。

1.1 基于ANCF索梁单元的绳索动力学建模

消旋机器人末端的柔性减速刷采用基于绝对节点坐标法(Absolute Nodal Coordinate Formulation, ANCF)索梁单元的绳索动力学进行建模。

1.1.1 单元动能

由于柔索单元的形函数为常数，第j个柔索单元上任意一点的速度矢量可写为

(1)

式中：r为任意点的全局位置矢量；S为形函数；qc为广义坐标。

利用式(1)，柔索单元的动能可写为

(2)

1.1.2 单元内能

利用Bernoulli-Euler beam梁方程，柔性减速刷绳索受预紧力作用，单元正应力为

σ=Eε+σ1

(3)

式中：σ1为预紧力；E为弹性模量；ε为轴向应变。则柔索单元的内能表示为

(4)

式中：V为柔索单元体积。

1.1.3 动力学方程

柔索系统的总动能和总应变能为

(5)

柔索系统的动力学方程为

(6)

式中：D为约束方程；λ为约束方程对应的拉氏乘子；Qe为广义力矢量；qc和λ都是未知量。

1.2 接触碰撞动力学建模

消旋过程中，接触碰撞主要发生在柔性减速刷与翻滚目标的帆板之间。基于非线性弹簧阻尼模型建立柔性减速刷与目标的接触碰撞模型。根据Hertz碰撞理论，接触碰撞表示为

(7)

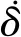
1.3 自由漂浮空间机器人动力学建模

自由漂浮空间机器人动力学方程为

(8)

式中：Hb为基体惯性矩阵；Hm为机械臂惯性矩阵；Hbm为空间机器人耦合惯性矩阵；xb为基体位置；qm为机械臂关节角度；cb为基体的非线性项；cm为机械臂的非线性项；Fb、Fe分别为作用于基座和末端上的作用力；τ为机械臂关节力矩；Jb为末端基体雅可比矩阵；Jm为末端关节雅可比矩阵。

1.4 基于计算力矩法的滑模控制

为提高消旋机构的效率以及维持机械臂的稳定，本文采取基于计算力矩法的滑模控制，进行翻滚非合作目标的消旋。

由于自由漂浮空间机器人末端作用力不能准确预知，因此假设末端作用力为零，可得动力学模型为

(9)

机械臂模型的惯性参数不能确定，根据计算力矩法，设计控制率为

(10)

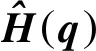
闭环系统方程为

(11)

则

(12)

(13)

若惯性参数估计值可逆，则闭环系统方程为

(14)

定义

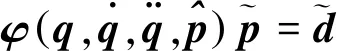
(15)

设计滑模函数为

(16)

(17)

取

(18)

式中：d为待设计的向量。

则

(19)

选取

(20)

定义Lyapunov函数：

(21)

则

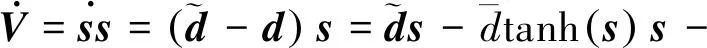
ηtanh(s)s≤-η|s|≤0

(22)

由式(10)和式(18)，得滑模控制率为

(23)

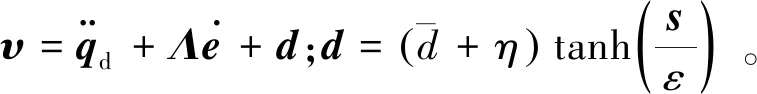
2 仿真结果

为验证所设计的柔性减速刷消旋策略及滑模控制方法，本节对使用冗余机械臂消旋翻滚卫星进行了仿真分析。冗余自由度机械臂具有七自由度，漂浮基座具有六自由度，空间机器人结构如图2所示，其动力学参数如表1所示。

待消旋翻滚目标参数如表2所示，分为PD控制和滑模控制两种，进行翻滚目标消旋对比，初始时刻以π rad·s-1速度绕-X轴方向进行旋转。

图2 空间机器人结构Fig.2 Structure of space robot

表1 动力学参数Table 1 Dynamics parameters

表2 翻滚目标参数Table 2 Parameters of tumbling target

在消旋过程中，由于翻滚目标帆板与减速刷之间的接触碰撞，导致翻滚目标能量耗散，角动量减小，旋转轴方向的角速度下降，并最终实现消旋，仿真过程如图3所示。碰撞后，柔性减速刷的振动明显，末端参数未知，不利于漂浮基座空间机器人的控制。

2.1 PD控制

针对柔性减速刷的消旋过程，采用PD控制以维持机械臂末端消旋机构的位置姿态。其中，控制参数取为Kp=60,Kd=40。

机械臂关节角度变化如图4所示。采用PD控制的消旋过程中，前期机械臂关节角度变化较为剧烈，每次碰撞后不能迅速恢复初始姿态，就开始进行下一阶段的消旋。后期，随着翻滚目标的自旋角速度的下降，自由漂浮空间机器人有充足时间进行位置姿态的调整，因此稳定性增强。

图3 翻滚目标消旋过程Fig.3 Spinning process of tumbling target

图4 基于PD控制的机械臂关节角度Fig.4 Joint angle of mechanical arm based on PD control

如图5所示，空间机器人的基体角度最终收敛，恢复初始角度。但在消旋过程中，基体角度时刻有偏差，未能呈现阶段性收敛，这对于消旋效率造成一定影响。如图6所示，经减速刷消旋后，快速翻滚目标绕旋转轴角速度降低，在较短时间内实现消旋。相对于自旋轴X轴，在其他方向上，角速度变化并不明显。

图5 基于PD控制的基体角度Fig.5 Angles of base based on PD control

图6 基于PD控制的翻滚目标角速度Fig.6 Angular velocities of tumbling target based on PD control

现定义，空间中任意翻滚目标，当其消旋程度达到90%时，即判定消旋成功。采用PD控制消旋过程，在80 s内，翻滚目标消旋程度为93%。消旋成功所需最短时间为68 s。

2.2 基于计算力矩法的滑模控制

机械臂关节角度变化如图7所示。为使减速刷末端到达期望位置，空间机器人基体应受控，即保持空间姿态稳定，空间机器人基体角度变化如图8所示。

图7 基于滑模控制的机械臂关节角度Fig.7 Joint angles of arm based on sliding mode control

图8 基于滑模控制的基体角度Fig.8 Angles of base based on sliding mode control

相对于PD控制，采用基于计算力矩法的滑模控制，使得高速旋转目标与柔性减速刷之间的碰撞力对于机械臂影响不大，机械臂各关节角度和基体角度数值变化相对较小，可迅速恢复初始状态，完成下一次消旋的准备。在消旋过程中，基体在翻滚目标旋转轴方向的角度变化较小，相对于PD控制，能够迅速收敛，具有快速响应能力。

由于帆板与减速刷之间的接触碰撞，翻滚目标所受碰撞力并不作用于质心上，而是与质心之间有一定的偏移，因此在角速度降低的同时，位置也随之发生变化，且随着消旋过程的不断进行，其线速度呈增长趋势，如图9所示。在消旋后期，由于消旋效率的降低，翻滚目标线速度呈现阶段性增长。令空间机器人追踪翻滚目标的轨迹，如图10所示，同时稳定机械臂末端的相对位置姿态，有利于提高消旋效率，抑制章动产生，创造消旋条件。

图9 基于滑模控制的速度追踪误差Fig.9 Deviation of speed tracking based on sliding mode control

图10 基于滑模控制的位置追踪误差Fig.10 Deviation of position tracking based on sliding mode control

由图11可知，经过滑模控制下机械臂末端的柔性减速刷消旋，翻滚目标绕旋转轴角速度显著下降，在80 s内消旋程度为92%，消旋程度达到90%所需的最短时间为57 s。滑模控制下的消旋所需时间小于PD控制下的消旋时间，消旋效率得到提高。

消旋过程呈现阶段性效果，随着消旋效率的降低，阶段性愈发明显。不仅体现在每次消旋的等待时间不断延长，还表现为翻滚目标角速度下降程度不断增大。同时由于柔性减速刷与目标帆板碰撞的不确定性，翻滚卫星在实现消旋目标的同时，在其他两轴产生章动，如图12所示。滑模控制下，翻滚目标在Y轴、Z轴方向上的角度变化较小，相对于PD控制幅值降低50%，对于进一步消旋影响不大。滑模控制有效降低了翻滚目标的章动程度，对目标进一步的抓捕消旋提供了良好条件。

图11 基于滑模控制的翻滚目标角速度Fig.11 Angular velocities of tumbling target based on sliding mode control

图12 基于滑模控制的翻滚目标角度Fig.12 Angles of tumbling target based on sliding mode control

3 结 论

1) 应用漂浮基座空间机器人动力学，对七自由度机械臂进行控制。基体成功追踪翻滚目标轨迹，保持机械臂及基座的姿态稳定。

2) 采用基于计算力矩法的滑模控制策略，对于七自由度机械臂进行控制，使其能在较大接触碰撞后迅速恢复原位。该策略不依赖末端负载的惯性参数，可应用于参数不确定的柔性减速刷消旋模式，具有快速响应、对参数变化及扰动不灵敏的特点。

3) 通过针对PD控制和滑模控制的仿真对比，结果表明减速刷消旋策略具有可行性与有效性，能够成功消除高速翻滚卫星的初始旋转速度，消旋程度均为90%以上。在相同时间内，滑模控制优于PD控制，有利于机械臂消旋姿态稳定，提高消旋效率。