浅谈由动点产生的等腰三角形存在性问题的转化策略

☉上海市岭南中学 刘华为

众所周知，构图、分类和求值是处理因动点产生的等腰三角形存在性问题的三大基本步骤.其中构图较易操作（主要以某条边为基准，若该边为底边则作其垂直平分线；若该边为腰则分别以其两端点为圆心、长为半径画圆，即可得满足条件的三个等腰三角形），分类（即以三角形的三边两两相等分三种情况讨论）也不棘手，但究竟如何求值不易把握，甚至常常有束手无策之感.本文不揣浅陋，就求值的转化策略谈几点肤浅的认识，以抛砖引玉.

一、转化策略

1.利用三边两两相等分类列方程转化

例1（2018年上海虹口一模第25题）如图1，已知AB=，点C、E分别为射线BG上的动点（点C、E都不与点B重合），连接AC、AE，使得∠DAE=∠BAC，射线EA交射线CD于点F.设

（1）当x=4时，求AF的长；

（2）当点E在点C的右侧时，求y关于x的函数关系式，并写出函数的定义域；

（3）连接BD交AE于点P，若△ADP是等腰三角形，直接写出x的值.

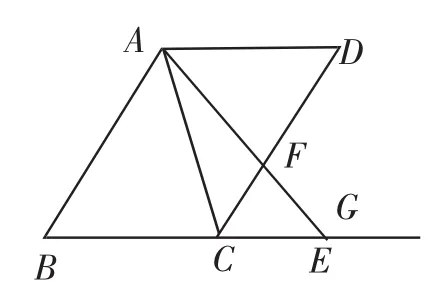
图1

图2

思路剖析

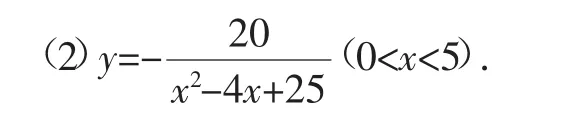
（3）对于△APD而言，由于AD=4，因此若能把AP和DP用含x的代数式表示，然后依据PA=PD、AP=AD和DA=DP三种情况分别列方程即可求出相应的x值.注意到△APD △EPB，则即则问题转化为EB、AE和BD的值（或用含x的代数式表示）.由∠BAC=∠DAE=∠BEA和∠ABC=∠EBA，知△BAC △BEA，依据对应边成比例可得而要求AE和BD的值，自然想到分别过点A、D作BC的垂线AM与DN（垂足分别为M与N，如图2），构造直角三角形求解，易得代入前一比例式可得然后列方程可解得x的值分别为和表面上看，本解法所列方程的形式与过程较复杂，但求解相当便捷，大可不必畏“繁”而退.

说明：利用三边两两相等处理等腰三角形存在性问题的转化策略，其优越性在于：思维指向十分明确，解题思路较为单一.因此，若所涉三角形的三边易求（或用相关变量表示），运用本转化策略处理往往可化难为易.

2.利用定角的三角函数转化

例2（2018年上海松江一模第25题）如图3，已知△ABC中，∠ACB=90°，AC=1，BC=2，CD平分∠ACB交边AB于点D，P是射线CD上一点，连接AP.

（1）求线段CD的长；

图3

（2）当点P在CD的延长线上，且∠PAB=45°时，求CP的长；

（3）记点M为边AB的中点，连接CM、PM，若△CMP是等腰三角形，求CP的长.

思路剖析：（1）过点D作DE∥AC，交BC于点E.由以及勾股定理，得

图4

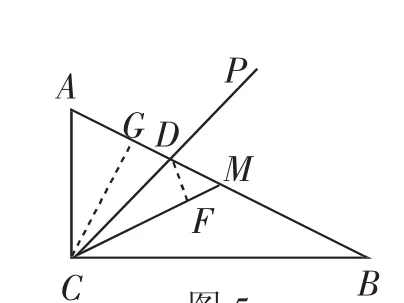
图5

如何求∠MCP的余弦值呢？自然想到重新构造直角三角形，即过点D作DF⊥CM，垂足为F（如图5），则问题又转化为求DF的长了.由△CDM的面积想到过点C作CG⊥AB，垂足为G.易求得所以进而得故CP=其实，辅助线CG一旦作出，由∠BCD=∠ACD和∠BCM=∠B=∠ACG，可直接求得cos∠MCP=所以辅助线DF也无需构造了，计算量自然大大减少.

若CP=MP（如图6），构造直角三角形CPQ，求出CP=也就是手到擒来之举了.

说明：当所研究的三角形中既有定角又有定边时，可借助“等腰三角形三线合一”构造直角三角形，并通过解直角三角形求出相关量.

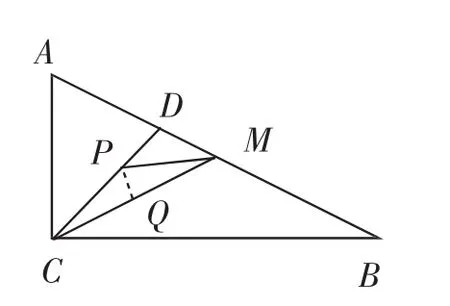
图6

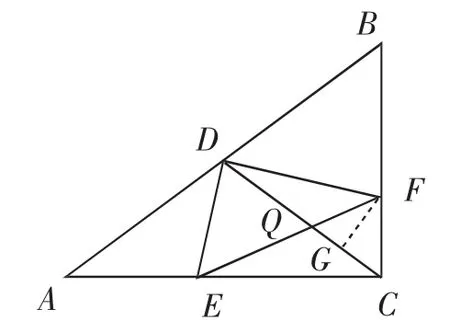
图7

例3（2018年上海崇明一模第25题）如图7，已知△ABC中D是AB边的中点，E是AC边上一点，连接DE，过点D作DF⊥DE交BC边于点F，连接EF.

（1）当DE⊥AC时，求EF的长.

（2）当点E在AC边上移动时，∠DFE的正切值是否会发生变化？如果变化，请说出变化情况；如果保持不变，请求出∠DFE的正切值.

（3）连接CD，交EF于点Q，当△CQF是等腰三角形时，请直接写出BF的长.

思路剖析：（1）EF=5.

（3）因为BC=6，所以要求BF实际上就是求CF的长.显然，在△CQF中，∠QCF=∠B是一定角，且正、余弦值分别是与但与例2不同的是，其三边CQ、CF与QF均是变量，不能像例2一样直接解直角三角形求出CF的长，需引入变量，不妨设CF=5m.

若FQ=FC=5m，过点F作FG⊥CQ，垂足为G（如图7），则CQ=2CG=6m.下面只需构造等式，列出关于m的方程即可.注意到tan∠DEF=tan∠A，所以∠DEF=∠B=∠QCF，则△DEQ △FCQ，则由于比例式中ED、EQ、DQ均不能直接用m表示，所以需再引入新变量，注意到DE∶DF∶EF=3∶4∶5，所以可设DE=3n，EF=5n，故，解得进而得

若CQ=FQ，则过点Q作QH⊥CF，垂足为H（如图8）.易得所以解得m=故BF=3.

当然，对于CQ=FQ时，由∠QFC=∠QCF=∠B和∠DFE=∠A，可得∠DFC=90°，进而得EF∥AB，易得BF=3.

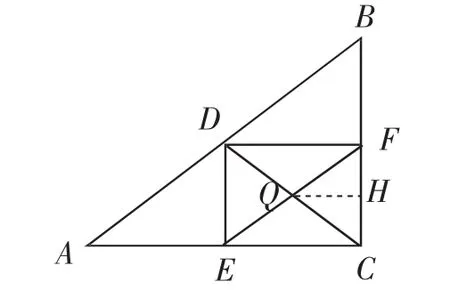
图8

不过前者与另两种情形融为一体，是通性通法，而后者虽然简捷，但技巧性强，自然应用的局限性也强.

说明：当等腰三角形中只有定角而缺少定边时，可巧设变量先把三边表示出来，再借助其他条件列方程（组）求解.

3.利用相似三角形华丽转身

例4（2016年上海市徐汇区一模第25题）如图9，四边形ABCD中，∠C=60°，AB=AD=5，CB=CD=8，P、Q分别是边AD、BC上的动点，AQ和BP交于点E，且∠BAD，设A、P两点的距离为x.

（1）求∠BEQ的正切值；

图9

（3）当△AEP是等腰三角形时，求B、Q两点的距离.

思路剖析：（1）由∠BAD和AB=AD、CB=CD想到连接AC，得再由∠BAD想到连接BD，交AC于点O，则∠BEQ=∠ABO，得其正切值为

（2）易证△AEP △ADF和△BEF △BDP.由对应边成比例可得

（3）对于△AEP而言，由于三个内角均非定角且三边都不易求解，所以直接处理颇为棘手，但若借助与其相似的△ADF转化，则可巧夺天工.

在△ADF中，若AF=AD=5，则Q、F、E均与点B重合，∠BEQ不存在，故不成立.

若AF=DF，由∠DAF=∠ADF＜∠DAO，知点F在线段OD上，此时点Q不在边BC上，也不成立.

若FD=AD=5，则BF=3，FO=1.不妨设BQ=t，下面只需列出关于t的方程（即寻找含有t的相关线段的等式）即可.注意到∠CBD=60°，所以过点Q作QG⊥BD，垂足为G，则且代入相关量即可求得

说明：若所研究的三角形中有多个相似三角形，应选择存在定角（定边）或边长易用相关变量表示的三角形，再依照前面的策略逐步转化求解.

二、两点思考

1.习题教学应以加强学法指导为抓手

数学教学离不开习题教学，但究竟如何开展习题教学常常是仁者见仁智者见智，很难有统一标准.不过笔者觉得习题教学至少要以学法指导为抓手，从知识转化角度切入，剖析解题思路的生成过程，充分挖掘解题策略形成的必然性与操作性，从而引导学生学会“怎样想”，提升他们分析问题和解决问题的转化能力.如“腰相等”“底角相等”“三线合一”是等腰三角形的三个重要性质，当然也是处理由动点产生的等腰三角形存在性问题的三大切入点.本文的四道例题均是先由这三个性质切入（其中例1由“边相等”直接切入；例2则是由“边相等”和“三线合一”共同打开解题思路；例3更是把三者进行了有机融合后打通思维通道；例4是从“边相等”和“角相等”入手使问题迎刃而解），一举找到解题思路的突破口，再逐步完善转化过程，值得细细品味.

2.解题教学应以追求以题会类为境界

习题永远做不完，但处理同类问题的策略或方法就那么多.因此，如何精选例题，以涵盖同类问题的常见类型与处理问题的基本策略，着重培养学生的类化能力和迁移能力，力求达到“以题会类”的习题教学最高境界，恐怕是值得每位执教者深入思考与扎实推进的课题.对于由动点产生的等腰三角形存在性问题而言，用相关变量表示出三边（或求出具体值）再依据两两相等分类列方程求解是处理问题的基本策略（如例1），但当三边不易用含变量的代数式表示时，可借助某一定角的三角函数巧妙转化（如例2、例3）；若不仅三边不易表示而且没有定角，则可借助与其相似（含全等）且符合上述特征之一的三角形转化（如例4）.经此提炼，学生面对“等腰三角形存在性问题”就有了明确的思考方向与转化策略，处理起来自然就更加得心应手了.

当然，随着情境的变化和综合性的强化，处理由动点产生的等腰三角形存在性问题的转化策略也会不尽相同.但只要我们做个有心人，深入挖掘解决问题的本质，就一定能不断归纳出处理问题的通性通法，追求“以题会类”的习题教学最高境界，从而摆脱“题海战术”的桎梏，真正把“减负增效”落到实处，最终提升自己造福学生.