机电集成电磁蜗杆传动机械系统灵敏度分析
关雪梅,郝秀红
(1.燕山大学 车辆与能源学院,河北 秦皇岛 066004;2.燕山大学 机械工程学院,河北 秦皇岛 066004)
0 引言
机电集成电磁蜗杆传动是有源、无接触的广义复合运动,该传动利用磁铁的特性,结合电机学、电磁学和机械学而发展起来的一种新型非接触传动形式,它集蜗杆传动和电动机功能于一体,进一步增强了蜗轮蜗杆传动的功能,该传动与传统齿轮传动相比具有效率高、系统无需润滑、噪声小、结构紧凑等特点[1]。
该传动机构是集机、电、磁于一体的机电耦合广义复合传动系统,包括电系统、机械系统及其耦合部分,机构各个系统各个环节之间参数变化是相互影响的,机电集成电磁蜗杆传动系统灵敏度分析就是找出机械系统的动态特性对哪些参数的变化较为灵敏,进而对这些参数做出相应修正的过程[2-4]。使用灵敏度分析可以简化优化设计过程,提高设计效率。
现有的电磁场的耦合场分析方法多为机电耦合系统的平面单自由度动力学建模及仿真[5-6],该方法在研究磁场与转矩随设计参数变化规律时没有解析法灵活[7-8],不能给出系统刚度的解析公式,不便于系统灵敏度的分析。
对广义复合传动系统灵敏度分析的方法主要有直接计算法、高阶函数法和一阶函数法[9-12]。直接计算法计算量大且可行性较差;高阶灵敏度函数法难于求解且没有实用性,目前灵敏度分析大多选用的是一阶灵敏度函数法,本文采用一阶灵敏度函数法推导出系统灵敏度矩阵,在初选结构参数的基础上,研究机械系统主要结构参数对电磁啮合的影响规律,为机电集成电磁蜗杆传动的加工制造提供依据。
1 电磁蜗杆传动系统动力学模型建立
电磁蜗杆传动系统的动力学模型如图1所示[13]。为了方便起见,用相应的啮合位移代替旋转位移
ui=riθi,
(1)
其中,i=p,w,θp、θw为蜗轮、蜗杆转动的角度,rp、rw是蜗轮、蜗杆的基圆半径。
蜗杆蜗轮系统矩阵形式可表示为蜗轮位移向量X及与之相应的质量矩阵M的运动微分方程,
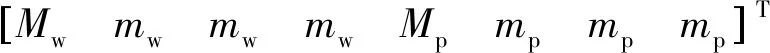

传动系统动力方程如下

(2)
式中,pwp为蜗杆和蜗轮之间的相对位移(mm);kwp为蜗杆与蜗轮之间的扭转电磁啮合刚度(N/m)。
此系统模型中蜗轮与蜗杆线圈间的电磁耦合力及电磁耦合刚度与安装有扭矩输出部件是相同的,由系统的能量函数求导,并考虑螺旋升角的影响可得蜗轮与蜗杆线圈之间的电磁啮合刚度为
IiIjcosγ=Ccos(z1θ′+φv/3np)|θ=θ0,
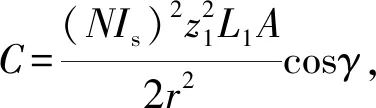
式中,kxw、kyw、kzw为蜗杆在x、y、z方向的支撑刚度(N/m);kxp、kyp、kzp为蜗轮在x、y、z方向的支撑刚度(N/m);δ为电磁力与蜗轮圆周的夹角(°);γ为蜗轮与蜗杆接触点处的导程角(°)。

图1 电磁蜗杆传动系统动力学模型
Fig.1 Dynamic model of the electromagnetic worm drive system
由图1可知,蜗杆和蜗轮之间的相对位移pwp计算如下
pwp=(uww-zp)cosδcosγ+(up-zw)cosδsinγ+
(xp+yw)sinδ,
(3)
将式(3)代入式(2)可得蜗杆蜗轮系统矩阵形式的运动微分方程为
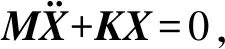
(4)
其中,

(5)
2 机械系统灵敏度分析
电磁蜗杆传动系统自由振动运动微分方程如式(4)所示,与其相对应的特征值方程为[13]

(6)

(7)


(8)

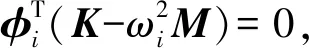
(9)
将式(6)和式(9)代入式(8)简化得
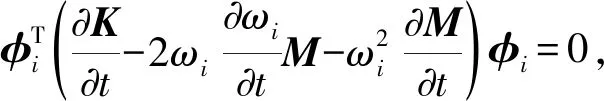
(10)
由式(10)可得
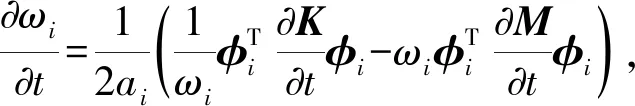
(11)



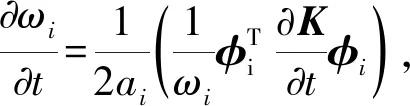
(12)

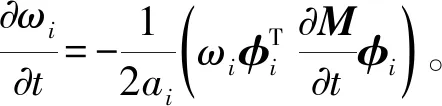
(13)
2.1 固有频率对电磁力与蜗轮圆周夹角δ的灵敏度
由式(12)可得固有频率对电磁力与蜗轮圆周夹角δ的灵敏度计算公式为

(14)
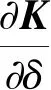
2.2 固有频率对比值a/r的灵敏度
比值a/r就是传动系统中的装配中心距a与环面蜗杆喉部计算圆半径r的比值,由式(12)可得固有频率对比值a/r的灵敏度计算公式为

(15)
由于蜗轮与蜗杆啮合点的导程角γ为比值a/r与传动比i的函数,即
可得蜗轮与蜗杆啮合点处的导程角对比值a/r的导数为

(16)
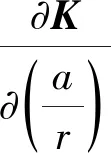
2.3 固有频率对传动比iwp的灵敏度
由式(10)可得固有频率对传动比iwp的灵敏度计算公式为

(17)
由于蜗轮与蜗杆啮合点的导程角γ为比值iwp的函数,可得蜗轮与蜗杆啮合点处的导程角对比值iwp的导数为

(18)
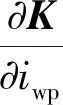
3 机械系统灵敏度分析
表1是整体传动系统设计参数,将参数代入相对应的公式,可得到固有频率对这些参数的灵敏度变化曲线如图2~4所示。
表1 算例系统参数
Tab.1 The system parameters of calculation example

变量取值Mw/kg4.5mw/kg9.0Mp/kg1.5mp/kg3.0kwp/(N/m)1.5×106kxw/kyw/kzw/(N/m) 2.0×106kxp/kyp/kzp/(N/m)1.5×106δ/(°)0/10i8a/R2
图2 固有频率对δ的灵敏度
Fig.2 The sensitivity of natural frequency forδ

图3 固有频率对比值a/r的灵敏度
Fig.3 The sensitivity of natural frequency fora/r

图4 固有频率对比值iwp的灵敏度
Fig.4 The sensitivity of natural frequency foriwp
由灵敏度曲线可得出如下规律:
1) 单个不重复且不等于零的3个固有频率,随着电磁力与蜗轮圆周的夹角δ的增加而减小,此三频率相应的振动模态为旋转模态。随着电磁力与蜗轮圆周的夹角δ的增加前3个模态的灵敏度递增,数值较大,且都为负值,蜗轮及蜗杆模态灵敏度始终等于零。其中,第一、第三模态的灵敏度较高,第二模态灵敏度较低。由灵敏度的定义可知,随着电磁力与蜗轮圆周的夹角δ的增加,前三模态的固有频率递减,且第一、第三模态固有频率递减较快,第二模态固有频率递减较慢,蜗轮及蜗杆模态固有频率不变。
2) 随着比值a/r的增加前三模态的灵敏度递减,数值很小,且都为负值,蜗轮及蜗杆模态灵敏度始终等于零。其中,第一、第三模态的灵敏度较高,第二模态灵敏度较低。由灵敏度的定义可知,随着比值a/r的增加,前三模态的固有频率递减,且第一、第三模态固有频率递增较快,第二模态固有频率递增较慢,蜗轮及蜗杆模态固有频率不变。
3) 随着传动比iwp的增加前三模态的灵敏度递减,数值较小,且都为负值,蜗轮及蜗杆模态灵敏度始终等于零。其中,第一、第三模态的灵敏度较高,第二模态灵敏度较低。由灵敏度的定义可知,随着传动比iwp的增加,前三模态的固有频率递减,且第一、第三模态固有频率递增较快,第二模态固有频率递增较慢,蜗轮及蜗杆模态固有频率不变。
4 结论
本文在前期研究基础上,利用解析法研究机电集成电磁蜗杆传动机械系统的动态特性,建立机械系统动力学模型,进行了机械系统灵敏度分析,结果表明电磁蜗杆传动机械系统自由振动的模态分蜗杆模态和蜗轮模态;机械系统的固有频率较低;对于每个磁极都有3个不同的固有频率相对应。
通过灵敏度分析,可以解决运行过程中机械结构振动的固有频率对传动随机参数的响应问题。在进行系统设计时,应当根据其运行工况确定外部激励源的频率,选择适当的方式改变系统设计参数从而改变系统固有频率避免共振现象的发生,进而设计出合理的蜗轮蜗杆传动系统,为机电集成电磁蜗杆传动系统的动力学设计和加工制造提供依据。

