最优单次重合跳频序列集设计
胡梦婷,牛宪华,韩 璐
(1.西华大学计算机与软件工程学院, 四川 成都 610039; 2.中科(广东)炼化有限公司, 广东 湛江 524076; 3.电子科技大学通信抗干扰技术国家级重点实验室, 四川 成都 611731)
跳频(frequency hopping,FH)码分多址(code division multiple access,CDMA)扩频系统有抗干扰、抗截获、安全可靠的特性,被广泛用于雷达、蓝牙、移动通信、军事无线电通信等领域[1-3]。在多址扩频通信系统中,众多用户可能工作在同一频段,如果在某一跳频时隙内多个用户的载频信号跳到相同的频隙上,造成碰撞,将引起用户间的多址干扰,可能使接收机的解调输出产生误码。干扰的大小与跳频序列(frequency hopping sequence,FHS)的汉明相关性能有直接关系。一般来说,汉明相关性越低,干扰次数越少。为区别通信中用户彼此的信号,防止相互干扰,采用的FHS的汉明相关值应尽可能小。FHS的汉明相关特性在FH-CDMA扩频系统中将起到非常重要的作用[1-2]。
FHS汉明相关的研究已有丰硕成果。1974年,A. Lempel 等[4]首先推导出对于单条FHS的理论界。2004年,Peng等[5]推导出对于FHS集的周期汉明自互相关函数的理论下界。基于不同数学工具,研究者构造出很多满足这些理论界的FHS或FHS集[6-9]。
另一方面,单次重合(one-coincidence,OC)FHS集自相关保持为0,互相关为1,可以最大限度地提高频率的使用率,降低频率的碰撞,因此被广泛用于多址通信中。20世纪80年代,Shaar等[10]首先为FH-CDMA引入了OC-FHS。2006年,Cao等[11]提出了OC-FHS集,并表明存在一些没有任何相应构造的OC-FHS集。2008年,Peng等[12]在基于素数有限域上,利用剩余类作为特殊的数学结构,给出素数长度的最优 FHS集的构造。2015年,Wang 等[13]利用笛卡尔积提出了关于OC-FHS集的构造。另外,利用中国剩余定理(Chinese Remainder Theorem,CRT)可将多维向量形式的FHS集转化为经典FHS集[12-16]。2014年,Chung等[14]利用中国剩余定理,给出了常规跳频序列集的扩展构造。本文将利用中国剩余定理,给出OC-FHS集的扩展构造,构造了3类新的满足Peng-Fan界最优的OC-FHS集。
1 预备知识
设频隙集F={f0,f1,…,fλ}大小为λ,集合S是在频隙集F上由M个序列长度为N的跳频序列组成。对于跳频序列集S中任意2条跳频序列x={x0,x1,…,xN-1}和y={y0,y1,…,yN-1},在相对时延τ下,跳频序列周期汉明相关函数的定义为
(τ=0,1,2,…,N-1)
(1)
其中,i+τ是modN运算,且当x=y时,式(1)为周期汉明自相关函数,当x≠y时,式(1)为周期汉明互相关函数。
对于跳频序列集S,其最大周期汉明自相关Ha(S),最大周期汉明互相关Hc(S),最大周期汉明相关Hm(S)分别定义为:
Ha(S)=max{H(x,x;τ)|x∈S,
τ=0, 1,…,N-1};
Hc(S)=max{H(x,y;τ)|x,y∈S,
x≠y,τ=0, 1,…,N-1};
Hm(S)=max{Ha(S),Hc(S)}。
令Ha=Ha(S),Hc=Hc(S),Hm=Hm(S)。
2004年,Peng等[5]建立了跳频序列集最大周期汉明相关理论界。
引理1(Peng-Fan界) 在大小为λ的频隙集F上,对于序列长度为N、序列数目为M的跳频序列集S,有
(2)
如果跳频序列集S的参数能够满足不等式(2),使得等号成立,则跳频序列集S是最优跳频序列集,并且是关于最大周期汉明相关最优。
2010年,Niu等[17]建立了跳频序列集的周期部分汉明相关函数的理论界。
引理2(Niu-Peng-Liu 界) 在大小为λ的频隙集F上,对于序列长度为N、序列个数为M、相关窗长度为L(L≤N)、起点为j的跳频序列集,有
(3)
当L=N时,引理2表示为跳频序列周期汉明相关理论界。如果跳频序列集S的参数能够满足不等式(3),使得等号成立,则跳频序列集S是满足最大周期部分汉明相关的最优跳频序列集。
本文将使用以下符号。
[x]v:表示对于整数x和正整数v,x模v的最小非负剩余。
「x⎤:表示大于或等于x的最小整数。
⎣x」:表示小于或等于x的最大整数。
Zq:表示对于正整数q的模q的整数环。
2 跳频序列集的构造
令q是一个奇素数,t是一个小于q的正整数,且gcd(q-1,t)=1。已知t阶剩余类FHS集S(q,t)在Zq上的定义为
其中
引理3[12]FHS集S(q,t)具有以下特性。
1)对于FHS集S(q,t)中的任意1条FHS都有Ha=0。
2)对于FHS集S(q,t)中的任意2条FHS都有Hc=0。
3)对于FHS集S(q,t),序列长度N与频隙集大小λ相同,即N=λ=q。另外,FHS集S(q,t)的每个频隙点都出现q-1次。
4) FHS集S(q,t)中的FHS的每个元素都不相同,即S(q,t)是单次重合FHS集。
5) FHS集S(q,t)中的任意1条FHS都满足Peng-Fan界最优,且FHS集S(q,t)是满足Peng-Fan界最优的OC-FHS集。
基于最优OC-FHS集,可以构造具有新参数的OC-FHS集。由CRT可知,当正整数u与v满足gcd(u,v)=1时,存在任意正整数k(0≤k≤uv)都能满足k=(ku,kv),其中ku=〈k〉u,kv=〈k〉v。
定理1 对于OC-FHS集,在任意相关窗长度L(1≤L≤N)下都满足周期部分汉明相关最优。
证明由引理2和引理3(3)可知,
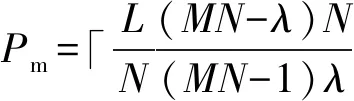

又由引理3(2)可得证。
证毕。
通过CRT可以将OC-FHS集S(q,t)扩展成新的FHS集。

其中k1=〈k〉n,k2=〈k〉q。
定理2 构造A中得到的FHS集G是(nq,nq,1,q-1)跳频序列集,且对于任意跳频序列Gi(0≤i 证明对于0≤i,j H(Gi,Gj;τ1,0)=H(Gi,Gj;τ1,τ2)= 分2种情况讨论。 情况1i=j,τ2=0,因此有 1)当τ1=0时有 2)当1≤τ1≤n-1时有 当i≠j或者τ2≠0 综合情况1和情况2,有 证毕。 推论1 对于构造A中的FHS集G有如下性质: 1)构造A中的FHS集G是OC-FHS集; 2)G是满足Peng-Fan界的最优跳频序列集; 3)G是满足Niu-Peng-Liu界的最优部分汉明相关跳频序列集。 证明由构造A可知跳频序列集G的序列长度N=nq,频隙大小λ=nq,序列个数M=q-1,依定理有Hm=1。 1)对于整数i,0≤i 相当于 (4) 2)根据Peng-Fan理论界,有 因此OC-FHS集G是满足Peng-Fan界的最优跳频序列集。 3)将参数代入不等式(3)中,对于任意相关窗长度L,1≤L≤N,都有 因此OC-FHS集G是满足最优周期部分汉明相关的跳频序列集。 证毕。 例1 根据构造A以及OC-FHS的定义,令q=5,t=3,则跳频序列集S={S0,S1,S2,S3},其中 S0={0,1,3,2,4},S1={0,2,1,4,3} S2={0,3,4,1,2},S3={0,4,2,3,1} 显然跳频序列S满足OC-FHS集参数要求,且最大周期汉明自相关Ha=0,最大周期汉明互相关Hc=1。令p1=7,p2=11,a1=a2=1,由构造A可知n=q1q2=77。利用构造A的方法,可以得到跳频序列集G,其中G0为 类似地可以得到跳频序列集G中的其他跳频序列: 对于0≤i,j<4,跳频序列集G的汉明相关为 由结果及推论1可知,根据构造A得到的跳频序列集G是满足Peng-Fan界的最优跳频序列集(385,385,1,4),对于跳频序列集G中的任意1条序列都满足Lempel-Greenberger界。结论与定理2以及推论1一致。 其中,k1=〈k〉pa-1,k2=〈k〉q。 由此构造了1个新的跳频序列集G={G0,G1,…,Gq-2}。 定理3 构造B中的跳频序列集G是((pa-1)q,paq,1,q-1)跳频序列集,且对于任意跳频序列Gi(0≤i 证明对于0≤i,j 分2种情况讨论。 情况1τ1=0,在这种情况下,有 因此 情况2τ1≠0,因为α是有限域Fpa的本原元,有 综合情况1和情况2,有 证毕。 推论2 对于构造B中的跳频序列集G有如下性质: 1)构造B中的FHS集G是OC-FHS集; 2)G是满足Peng-Fan界的最优跳频序列集; 3)G是满足Niu-Peng-Liu界的最优部分汉明相关跳频序列集。 证明令N=(pa-1)q,λ=paq,M=q-1,依定理有Hm=1。 1)对于整数i,0≤i 相当于 (5) 2)根据Peng-Fan理论界,有 因此OC-FHS集G是满足Peng-Fan界的最优跳频序列集。 3)将参数代入不等式(3),对于任意相关窗长度L,1≤L≤N,都有 因此OC-FHS集G是满足最优周期部分汉明相关的跳频序列集。 证毕。 例2 根据构造B令q=7,t=5,则跳频序列集S={S0,S1,S2,S3,S4,S5},其中 S0={0,1,4,5,2,3,6},S1={0,2,1,3,4,6,5},S2={0,3,5,1,6,2,4},S3={0,4,2,6,1,5,3},S4={0,5,6,4,3,1,2},S5={0,6,3,2,5,4,1}。 显然跳频序列S满足OC-FHS集的参数要求,且最大周期汉明自相关Ha=0,最大周期汉明互相关Hc=1。令p=11,a=1,α=1,利用构造B的方法,可以得到跳频序列集G,其中 类似的可以得到跳频序列集S′中的其他跳频序列: 对于0≤i,j<6,跳频序列集G汉明相关为 由结果及推论2 可知,根据构造B得到的跳频序列集G是满足Peng-Fan界的最优跳频序列集(70,77,1,6),对于跳频序列集G中的任意1条序列都满足Lempel-Greenberger界。结论与定理3及推论2一致。 表1 参数对比 本文构造的序列长度更长,汉明相关更小,且参数设置灵活。序列长度等于频隙集的大小,可以提高信道带宽的使用率,减小相互之间的干扰;因此,本文构造可以被广泛应用于多址通信。 本文利用中国剩余定理,构造了3类新的最优 OC-FHS集。通过这3个构造以及OC-FHS,可以构造更多新的满足理论界最优的OC- FHS集。

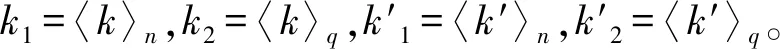

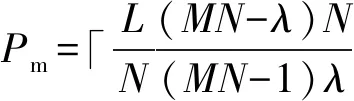
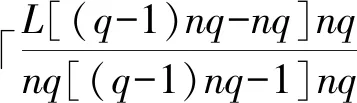
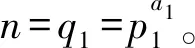
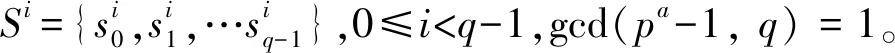



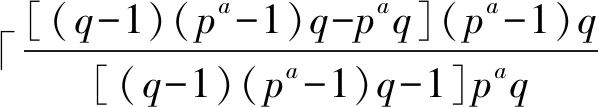
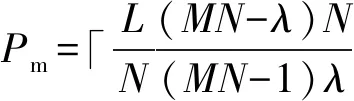
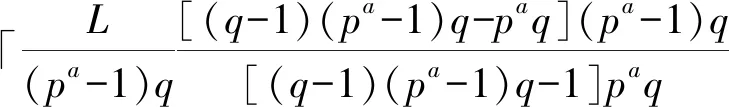

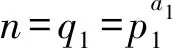

3 结论

