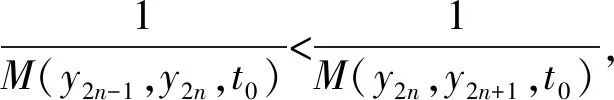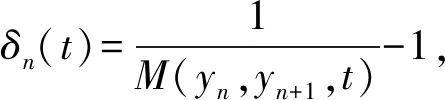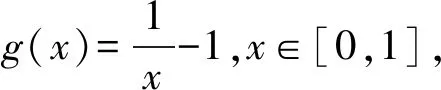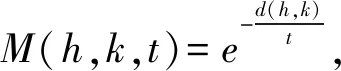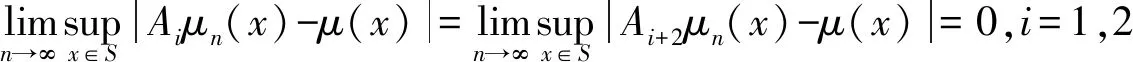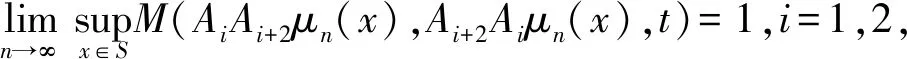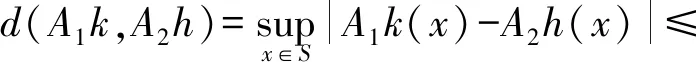模糊度量空间中公共不动点定理及其在动态规划中的应用
张树义,张芯语, 聂 辉
(渤海大学数理学院, 辽宁 锦州 121013)
1 引言与预备知识
关于模糊度量空间概念以及在此空间中建立的不动点定理,文献[1-15]做过广泛研究,这其中文献[14]引入模糊度量M满足三角不等式的概念,并在模糊度量空间中得到一些不动点定理。 文献[16]推广了上述相关结果,在模糊度量空间中研究了两类Φ-压缩映象的一些不动点定理,并讨论了一类泛函方程解的存在性。文献[17]在概率度量空间中研究了拓扑结构和度量化问题。近些年来,文献[18-26]研究了若干类非线性映象不动点的存在性。受上述工作启发,本文将文献[16]的结果推广到更一般的情形,在模糊度量空间建立了涉及4个映象的更广泛的Altman型映象的公共不动点存在性定理,从而改进和推广了文献[6-26]中的相应结果。作为应用,我们在模糊度量空间中还讨论了起源于动态规划的一类泛函方程组解的存在与唯一性。
定义1 映象*:[0,1]×[0,1]→[0,1]称为连续t-范数,如果满足以下条件:
(ⅰ) *是可结合和可交换的;
(ⅱ) *是连续的;
(ⅲ) ∀a∈[0,1],a*1=a;
(ⅳ) ∀a,b,c,d∈[0,1],若a 定义2 称三元组(X,M,*)是一模糊度量空间,若X是一任意非空集合,*是一连续t-范数,M是X×X×(0,+∞)上的模糊集,对∀x,y,z∈X和t,s>0,满足以下条件: (Ⅰ)M(x,y,t)>0; (Ⅱ)M(x,y,t)=1 当且仅当x=y; (Ⅲ)M(x,y,t)=M(y,x,t); (Ⅳ)M(x,y,t)*M(y,z,s)≤M(x,z,t+s); (Ⅴ)M(x,y,·)∶(0,+∞)→[0,1]是连续的。 如果(X,M,*)是一模糊度量空间,称(M,*)是X上模糊度量。 注1 设(X,Md,·)如例1所述是一标准模糊度量空间,则(X,Md,·)是完备的当且仅当度量空间(X,d)是完备的。 定义3 三元组(X,M,*)称为非阿基米德模糊度量空间,若(X,M,*)是一模糊度量空间,*是满足下列条件的*-范数。 (Ⅵ)M(x,z,max{t1,t2})≥M(x,y,t1)*M(y,z,t2),∀t1,t2∈[0,∞),∀x,y,z∈X。 George 和Veeramani[4]给出了如下结论 (ⅰ) 设(X,M,*)是一模糊度量空间,称B(x,r,t)={y∈X:M(x,y,t)>1-r},∀r∈(0,1),t>0为具有中心x∈X,半径r的开球。一族集{B(x,r,t):x∈X,0 (ⅱ) 模糊度量空间(X,M,*)中序列{xn}收敛于x当且仅当M(xn,x,t)→1(n→∞)。 (ⅲ) 模糊度量空间(X,M,*)中序列{xn}称为Cauchy序列,如果对∀r∈(0,1)和t>0,存在n0∈N(正整数集),使得n,m≥n0,M(xn,xm,t)>1-r。 模糊度量空间(X,M,*)称为完备的,如果每一Cauchy 序列{xn}在X中收敛。 定义4[8]设(X,M,*)是模糊度量空间,模糊度量M称为三角的,如果∀x,y,z∈X,∀t>0,有 注意到每个标准模糊度量(Md,·)是三角的。 设Ω={g|g:[0,1]→[0,∞) 连续,严格递减,g(1)=0}。 定义5 非阿基米德模糊度量空间(X,M,*)称为(C)g型的。如果存在g∈Ω,使得∀x,y,z∈X,∀t≥0,有gM(x,y,t)≤gM(x,z,t)+gM(z,y,t)。 定义6 非阿基米德模糊度量空间(X,M,*)称为(D)g型的,如果存在g∈Ω,使得∀s,t∈[0,1],有g(s*t)≤g(s)+g(t)。 定义7 设模糊度量空间(X,M,*),映象S,A:X→X称为相容映象,如果对{xn}⊂X,当 下列引理在后面将被用到 引理1 设(X,M,*)是模糊度量空间,S,A:X→X是相容映象,如果Az=Sz,z∈X,则ASz=SAz。 引理2 (ⅰ) 如果非阿基米德模糊度量空间(X,M,*)是(D)g型的,则(X,M,*)是(C)g型的。 这表明(X,M,*)是(D)g型的。证毕。 定义Φ1={φ:φ:[0,∞)→[0,∞) 是单调递增满足(c1),(c2)和(c3)},其中条件(c1),(c2)和(c3)如下: (c1) 0<φ(u) 注3 如果φ∈Φ1,则φ(0)=0且φ(u)=u⟺u=0。 定理1 设(X,M,*)是具有M三角的完备模糊度量空间,设(S,A),(T,B)是X→X的相容映象,AX⊂TX,BX⊂SX,使得∀x,y∈X,∀t>0,有 (1) 其中∀x,y∈X,t>0,Φ∈Φ1。如果S,T,A,B连续,则S,T,A,B在X上有唯一公共不动点。 证明任取x0∈X作序列 y2n=Ax2n=Tx2n+1,y2n+1=Bx2n+1=Sx2n+2(n=0,1,2,…),由(1) 对∀t>0,有 同理对∀t>0,有 于是对n=0,1,2,…,∀t>0,有 所以Bv=Au,于是Su=Au=Bv=Tv=c,进而由引理1有Sc=Ac,Bc=Tc。 于是对∀t>0,由(1)和(c1)有 所以Sc=Tc=Bc=Ac。下证c是S,T,A,B在X上公共不动点。由(1)和(c1)对∀t>0,有 所以Sz=Tz=Bz=Az=w。下证w是S,T,A,B在X上公共不动点。由于(S,A)是相容映象,故由引理1有Sw=ASz=SAz=Aw。 又因为(T,B)是相容映象,所以Tw=TBz=BTz=Bw。 由(1) 对∀t>0,有 于是w=Bw,故w是S,T,A,B在X上公共不动点。唯一性显然。证毕。 设(X,Md,*)是由X上度量d诱导的完备标准模糊度量,则Md是三角的,于是由定理1,我们有下列推论。 推论1 设(X,d) 是完备度量空间,(S,A),(T,B)是X→X的相容映象对,AX⊂TX,BX⊂SX,∀x,y∈X,满足如下不等式 如果S,T,A,B连续,则S,T,A,B在X上有唯一公共不动点。 定理2 设(X,M,*)是完备非阿基米德模糊度量空间,其中连续t-范数为a*b=min{a,b},a,b∈[0,1],再设(S,A),(T,B)是X→X的相容映象,AX⊂TX,BX⊂SX。使得∀x,y∈X,∀t>0,有 其中Φ∈Φ1。如果S,T,A,B连续,则S,T,A,B在X上有唯一公共不动点。 设R=(-∞,+∞),X和Y是实Banach空间,S⊆X为状态空间,D⊆Y为决策空间,B(S)是S上有界实函数全体,x和y分别为状态向量和决策向量,T为过程变换,f(x)为具有初始状态x的最优返回。下面我们利用在模糊度量空间中建立的涉及4个映象的Altman型映象的公共不动点定理,讨论下列起源于动态规划的泛函方程组解的存在与唯一性: (2) 其中i=1,2,3,4,x∈S,opt=sup或opt=inf,u:S×D→R,T:S×D→S,H:S×D×R→R。 定理3 假设下列条件成立: (a1)u,Hi(i=1,2,3,4)有界; (a2)对任意(x,ξ,y)∈S×S×D,k,h∈B(S)和t>0,有 对x∈S,y∈D,k,h∈B(S),t∈S,其中Φ∈Φ1, (a3)A1(B(S))⊆A4(B(S)),A2(B(S))⊆A3(B(S)); (a4)对Ai(i=1,2,3,4),满足任意的{γn}n≥1⊂B(S),γ∈B(S),有 (a5)对任意的{μn}n≥1⊂B(S),如果存在μ∈B(S),当 证明任意的h,k∈B(S),定义d(h,k)=sup{|h(x)-k(x)|,x∈S},由(a1)可知, Ai:B(S)→B(S),i=1,2,3,4。 由(a4)和(a5),A1,A2,A3,A4是连续的,并且A1与A3,A2与A4是相容的。 若opt=sup,则由(a2)中Aiqi(x)的定义,对任意的k,h∈B(S),x∈S,对任意的ε>0,存在y,z∈D,有下列不等式成立: A1k(x) A1k(x)≥u(x,z)+H1(x,z,k(T(x,z))),A2h(x)≥u(x,y)+H2(x,y,h(T(x,y)))。 由上面不等式容易得到 A1k(x)-A2h(x) 和 A1k(x)-A2h(x)>H1(x,z,k(T(x,z)))-H2(x,z,h(T(x,z)))-ε≥ 令ε→0,得 进而由条件(ⅱ)有 因此 (3) 如果opt=inf,类似的,(3)也成立。由定理2我们立刻获得A1,A2,A3,A4有唯一不动点w∈B(S),即w是泛函方程(2)在B(S)上的唯一解。证毕。
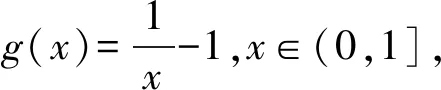


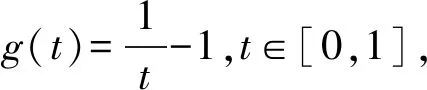


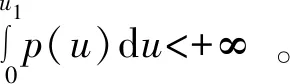
2 主要结果