关于四元数系数多项式特殊根的研究

姜莲霞

（喀什大学 数学与统计学院， 新疆 喀什 844000）

近年来，有关四元数系数多项式求根方法的研究引起国内外学者关注，并取得可喜成果[1-7]，如文献[8]给出了求四元数系数多项式纯虚数四元根的一种方法；文献[9]讨论了四元数系数多项式有某些特殊根的充分必要条件；文献[10]给出了毕达哥拉斯运动曲线可由次数较低的另一条曲线生成的充分必要条件是其生成四元数系数多项式有一个复根.

经典的Sturm算法是确定常系数多项式实根个数的一种有效方法[11]，但对于具有符号系数的多项式，该算法极不方便. 参数多项式完全根的分类已应用于多问题的研究中，并建立了多种方法[12-16]. 而对四元数系数多项式

的根进行计数和分类却未发现类似结果， H表示实四元数体.

本文通过构造从四元数系数多项式 Q(t)根的集合到由 Q(t)确定的某些实(复)多项式的实(复)根集合的一个双射，来确定 Q(t)的球形根、实根、孤立复根、纯虚数四元根，以及在或中根的集合.结果表明，实(复)系数多项式根的计数和分类适用于四元数系数多项式的根.

1 四元数

R、C 分别表示实数域和复数域，实四元数体 H中的元素形如q=x0+x1i+x2j+x3k，其中x0,x1,x2,x3∈R.q的共轭定义为=x0-x1i-x2j-x3k，q的实部和虚部分别为 Re q=x0和Imq=x1i+x2j+x3k.若Req=0，则称q 是纯虚数四元数；q的范数|q|定义为数量

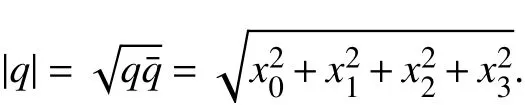
对两个四元数q 和q′，若使 得q′=wqw-1，则称它们等价，记作q∼q′.显然，q∼q′⇔Req=Req′且|q|=|q′|.q的等价类集合为

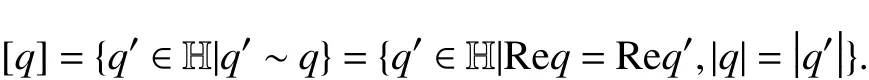
文献[13]指出，每个 [q] 恰√好包含复数z=x0+和其共轭

设H[t]是H上变量t的 多项式环. 每个f(t)∈H[t]可写成f(t)=a0tn+a1tn-1+···+an，其中n∈Z+，a0,···,且a0≠0.对，定义f(t)在q处的值为

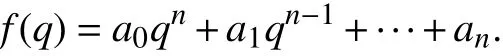
一般地，f(t)不是H[t]到H的环同态.若f(q)=0，则称四元数q 是f(t)的零点或根.

设q是 f(t)的一个根.若q不是实数且对∀z∈[q]，有 f(z)=0，则称q生成一个球形根，简称q 是球形根；若q是实数或不能生成球形根，则称它为孤立根；若等价类中有两个元素均为 f(t)的根，则该等价类中的所有元素都是f(t)的根[3]. 由于每个等价类恰好包含复数z和其共轭z，所以由 f(t)根 的复数对{z,z}可确定f(t)的所有球形根.

2 纯虚数四元数根

设Q(t)=antn+an-1tn-1+···+a0.当n 为奇数时，令；当n为偶数时，令h(t)=. 再设gi(t),hi(t)∈R[t],(i=1,2,3,4)使得g(t)=g1(t)+g2(t)i+g3(t)j+g4(t)k，h(t)=h1(t)+h2(t)i+h3(t)j+h4(t)k.用 E(t)表 示多项式g1(t),···,g4(t),h1(t),···,h4(t)的最大公因式. 考虑多项式

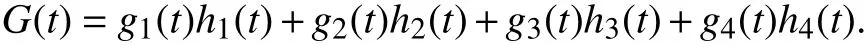
若令L (t)=gcd(F(t),G(t))， 则E (t)|L(t).

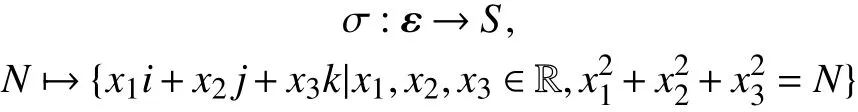
和

均是双射.

证明 设x=x1i+x2j+x3k≠0是Q(t)的一个纯虚数四元根，则.令有 x2=-N.因此，Q(x)=0意味着g(N)x+h(N)=0.进一步，因为x≠0，所以g(N)=0⇔h(N)=0.假设 x定义了Q(t)的一个球形根，则∀y∈[x]都有Q(y)=0. 因y 是满足|x|=|y|的 纯虚数四元数，故y2=-|y|2=-|x|2=x2≠0.于是，对∀y∈[x]有g(N)y=-h(N).从而，g(N)=h(N)=0 . 又因 N 是实数，且E (N)=0，故N∈ε.反过来，若，则g(N)=h(N)=0. 因此，对每个纯虚数四元数x，其中√，都有Q(x)=g(N)x+h(N)=0.于是，[x]是 Q(t)的一个球形根. 综上可知，σ 是双射.

因E(t)|F(t),G(t)，故E(t)|L(t). 设L(t)≠E(t) ，x是Q(t) 的满足g (N)h(N)≠0的孤立纯虚数四元数根. 于是，有g(N)x+h(N)=0，从而|g(N)|2|x|2=|h(N)|2. 所以，N 是F(t)的一个根. 此外，|g(N)|2. 又因Rex=0，故G (N)=0. 因此，N是L(t)的一个正实根，即N∈L.反过来，设N∈L，|g(N)|2. 因G(N)=0，故Rex=0.此外，由于 N 是F (t)的一个根，故.从而，x是纯虚数四元数且x2=-|x|2=-N ，Q(x)=g(N)x+h(N)=0. 综上可知，τ是双射.

推论1 Q(t)球形 根的数量等于E(t)正根的数量，同时，Q(t)的孤立纯虚数四元数根的数量等于L(t)的正根(非E(t)的根)数量.

推论2 设l1,···,lv是 L(t)的满足g(li)h(li)≠0,(i=1,···,v)的正实根. 于是，四元数qi=-g-1(li)h(li),(i=1,···,v) 均为 Q(t)的孤立纯虚数四元数根.

证明 因映射τ是双射，故 L(t)的 根(也是E (t)的根)ρ满足g(ρ)=h(ρ)=0，而其他的根则满足g(ρ)≠0和 h(ρ)≠0.因此，这些根ρ生成Q(t)的孤立纯虚数四元数根g-1(ρ)h(ρ).

3 球形根和中的根

设Q(t)∈H[t]C[t]且 deg(Q(t))≥1是首1多项式. 记

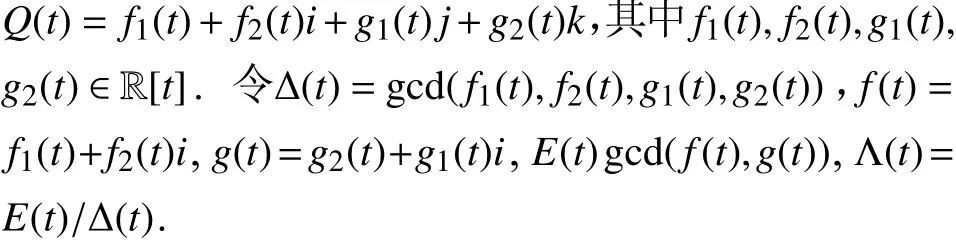
定理2 1) Q(t)的 实根集合与Δ (t)的实根集合相同；

2) Q(t)的球形根可由Δ(t)的一对共轭复根表示；

3) Q(t)的孤立复根集合与Λ(t)的根集合相同.

证明 1) 设x∈R.由Q(x)=0 ⇔f1(x)= f2(x)=g1(x)=g2(x)=0，即Δ(x)=0可知Q(t)的实根集与Δ(t)的实根集相同.

2) 设z∈C，由Q(t)= f(t)+kg(t) 可知Q(z)=0 ⇔f(z)+kg(z)=0，即f(z)=g(z)=0.假设Q(t)有一个球形根q，令z和z是q的等价类中唯一的一对共轭复数，则，即有且.由此可见，实系数多项式整除 f(z)和 g (z). 进而，整除多项式f1(t),f2(t),g1(t),g2(t).因此，z和z是Δ(t)的一对共轭复根.反过来，假设z和是Δ(t)的一对共轭复根.于是，z和z是f(t)和g(t)的根，进而是Q(t)的根. 因此，z 是Q(t)的一个球形根.可见，由Q(t)的球形根到Δ(t)的一对共轭复根之间存在一个双射.

3) 记Q(t)= f～(t)+ig～(t). 同理可证所要的结果.

4 应用举例

例1 求多项式P(t)=t3+(2+k)t+i-j的纯虚数四元数根.

解:沿用第3节的符号，g(t)=-t+2+k，h(t)=ij.于是，g1(t)=-t+2，g2(t)=g3(t)=0，g4(t)=1，h1(t)=h4(t)=0， h2(t)=1，h3(t)=-1，则它们的最大公因式E(t)=1.因此，P(t)无球形的纯虚数四元数根. 又多项式F(t)=((-t+2)2+1)t-(1+1)=t3-4t2+5t-2， G(t)=0.

于是，L(t)=gcd(F(t)，G(t))=t3-4t2+5t-2 . L(t)的实根为1 和2. 通过计算可得-g-1(1)h(1)=-(1+k)-1(i-j)= j，-g-1(2)h(2)=-k-1(i-j)= j+i. 因此，由推论2可知P (t)的 孤立的纯虚数四元数根是j和i+j.

例2 求多项式Q(t)=t6+jt5+it4-t2-jt-i的根.

解:沿用第4节的符号，f1(t)=t6-t2，f2(t)=t4-1，g1(t)=t5-t ，g2(t)=0.于是，Δ(t)=gcd(f1(t),f2(t),g1(t),g2(t))=t4-1.由定理2，Q(t)有 实根± 1，一对共轭复根t3=(1-i-j-k)/2,t4=(-1+i-j-k)/2和一个由t5=i生成的球形根.

例3 求多项式R(t)=t4-(2+k)t3+(3+j+2k)t2-2(1+j+k)t+2(1+j)的根.

解: 沿用第4节的符号，记R(t)= f(t)+kg(t)，其中f(t) = t4-2t3+3t2-2t+2 ，g(t) =-t3+(2+i)t2-2(1+i)t+2i. 于是，

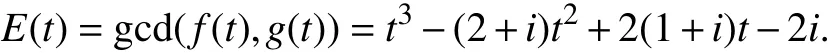
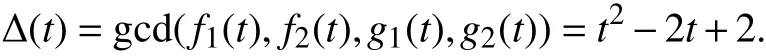
Δ(t)的共轭复根为1±i，其生成了R (t)的一个球形根. 因Λ(t)=E(t)/Δ(t)=t-i，故i是 R (t)的孤立复根.

沿用第3节的符号， g(t)=-2+2t-2 j+(-2+t)k，h(t)=2-3t+t2+(2-t)j-2tk . 于是，F(t)=28t-30t2+11t3-8-t4， G(t)=-4t+6t2-2t3. 于是，L(t)=gcd(F(t),G(t))=t2-3t+2=(t-1)(t-2)， -g-1(1)h(1)=i,-g-1(2)h(2)=k+i.因此，多项式 R(t)无其他根.

综上可知，R (t) 的孤立复根为i，纯虚数四元数根为i +k ，球形根为1 +i.