六自由度机械臂无模型自适应滑模控制

(广西大学电气工程学院， 广西南宁530004)

0 引言

工业机械臂是一个具有时变性、强耦合、强非线性等动力学特征的非线性系统，由于其数学模型复杂，在控制时通常将其进行近似线性化处理，同时忽略各个关节之间的耦合特性，即将多关节机械臂转化为数个独立的线性系统，再对简化后的系统分别采用PID等线性控制方法来实施控制。这样处理后得到的模型无法准确描述机器人系统的运动特性，且无法对系统存在的强非线性特性进行有效补偿，其控制效果较差。滑模控制在解决机器人控制问题上应用广泛，具有较强的鲁棒性、响应迅速、计算量小、物理实现简单等优点[1]。文献[2]提出了自适应模糊滑模控制算法对机器人控制，提高了鲁棒性，但模糊规则的调整需要基于一定的先验知识；文献[3]提出了全局快速终端滑模控制，但控制器的设计高度依赖系统模型信息，不易实现。传统的无模型控制策略虽无需建立机器人动态模型，但控制效果往往难以达到要求，而基于模型的控制策略其控制精度受所建模型精度的影响较大，控制律较为复杂。针对这些问题，很多学者提出了一些先进的无模型控制算法[4-5]。无模型自适应控制是一种数据驱动控制方法，其控制器的设计仅利用被控系统的I/O数据。控制器设计的基本原理是在满足一定假设的前提下引入伪偏导数，在离散系统的每个工作点处建立一个等价的虚拟动态线性化模型[6]。在这个虚拟动态线性化模型中，伪偏导数只需要被控对象的输入输出数据在线估计[7]。对于六自由度工业机械臂这类强耦合的复杂非线性系统，直接使用无模型自适应控制方法并不能保证跟踪误差快速收敛。

鉴于此，本文针对六自由度机械臂系统提出了一种无模型自适应滑模控制方案。该方案利用全格式动态线性化方法将机械臂非线性模型转换为离散的动态线性模型[8]，仅用到各关节的输入力矩和输出速度来设计控制器，同时引入滑模控制保证其收敛性。

1 动态线性化及控制器设计

1.1 六自由度机械臂数学模型

动力学模型建立普遍采用的方法有牛顿—欧拉方法、拉格朗日方法等等。本文利用Euler-Lagrange方法，不考虑外部未知干扰力作用，在关节坐标中建立六自由度机械臂的动力学模型[3]：

(1)

(2)

1.2 动态线性化部分

对于六自由度机械臂离散时间系统，各关节的角度、角速度、M(θ)、G(θ)等在k时刻分别是特定的值或矩阵，因此，机械臂系统在k时刻可以离散成如下形式：

(3)

(4)

(5)

Δy(k+1)=Φ1(k)Δy(k)+Φ2(k)Δu(k)，

(6)

证明：

Δy(k+1) =y(k+1)-y(k)

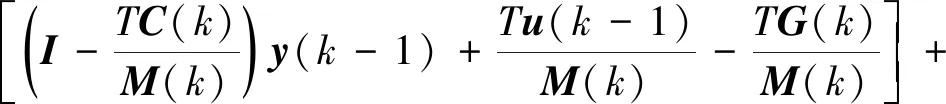
(7)

令

由Cauchy微分均值定理可知，式(7)可以被重新写成以下形式：

(8)

对于每一个固定的k，考虑以下等式

δ(k)=L(k)[Δy(k),Δu(k)]T，

(9)

y(k+1)=Φ1(k)Δy(k)+Φ2(k)Δu(k)+y(k)。

(10)

1.3 控制器设计

1.3.1 无模型自适应控制器

考虑如下的优化控制准则函数：

(11)

(12)

其中，ρ∈(0,1)是步长因子，它加入的目的是使控制算法更具有一般性。

用改进的投影算法估计未知的伪偏导数矩阵。考虑以下的伪偏导数阵准则函数：

(13)

式中，μ>0是一个权重因子，对式(13)关于Φ(k)求导，令其等于零，可得到：

(14)

式中，f=Δy(k)-(Φ1(k-1)Φ2(k-1))(Δy(k-1)ΔuM(k-1))T，η∈(0,1]是步长因子，它的加入是为了使式(14)更具有一般性。综合前面得到的伪偏导数估计算式(14)及控制算法式(12)，可以得到无模型自适应控制(Model Free Adaptive Control)方案。

1.3.2 无模型自适应滑模控制算法

对于六自由度机械臂的动力学转换形式(10)，令：

e(k)=yd(k)-y(k)，

(15)

假设离散滑模面为：

s(k)=e(k)，

(16)

则s(k+1)=e(k+1)=yd(k+1)-y(k+1)，因此，由式(10)得到：

s(k+1)=yd(k+1)-y(k+1)=yd(k+1)-y(k)-Φ1(k)Δy(k)-Φ2(k)Δu(k)，

(17)

进入理想滑动模态时需要满足：

s(k+1)-s(k)=-qTs(k)-εTsign(s(k))，

(18)

其中，ε>0，q>0，1-qT>0，T是离散采样周期。将式(17)代入式(18)可得到：

Δu(k)=Φ2(k)-1×(yd(k+1)-y(k)-Φ1(k)Δy(k)-(1-qT)s(k)+εTsign(s(k)))，

(19)

由于滑模到达性条件是基于动态线性化，令uSM(k)=Δu(k)，则最终的控制器的控制律是式(12)和式(19)相加，即：

u(k)=uM(k)+YuSM(k)，

(20)

其中，γ=diag{[γ1γ2γ3γ4γ5γ6]}∈R6×6，权重系数γj>0(j=1,2,…,6)的加入是为了令控制律更具有一般性，γ调节收敛的速度。整个控制算法的实现如图1所示。

图1 整体控制框图Fig.1 Overall control block diagram

仿真步骤：在采样时刻点获取机械臂连续非线性时变模型的输入力矩和输出速度数据；将输入和输出数据代入式(14)中，估计时变参数矩阵Φ(k)；将估计得到的参数矩阵、系统历史输入输出数据信息和期望轨迹分别代入到自适应控制律式(12)中和滑模控制律式(19)中，得到uM(k)，uM(k)uSM(k)；把uM(k),uSM(k)代入式(20)中解算出下一时刻所需的控制力矩，在下一采样时刻更新机械臂的控制量，重复上述循环直至仿真结束[10]。

总之，首先利用全格式动态线性化方法将机械臂连续非线性模型转换为离散的动态线性模型，用无模型自适应律式(14)估计动态线性模型的时变参数Φ(k)，然后结合滑模控制使误差逐渐趋近于零。伪偏导数是转换后的离散模型中最重要的待估计量，仅用到了各关节的历史输入力矩和输出速度数据信息在线估计。而基于模型的控制算法往往要结合精确的系统模型算式才能得出具体的控制律。无模型自适应控制算法为估计六自由度机械臂动态线性化模型提供了输入输出数据，引入离散滑模趋近控制律弥补了偏差，对跟踪误差的收敛起到了加速作用[11]。

1.3.3 稳定性分析

对于六自由度机械臂模型(5)，在满足y(k+1)关于关节角速度输出y(k)和力矩输入u(k)的偏导数是连续的并且满足广义Lipschitz条件下，当yd(k+1)和yd(k)相等且为一个常量时，控制方案由(12)、(14)、(19)、(20)组成，那么存在λ>0保证系统跟踪误差保持收敛且输入输出均有界。

证明：

(21)

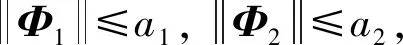
(22)

其次：由式(15)知e(k)=yd(k)-y(k)，有：

(23)

存在λ>0，ρ∈(0,1)使得

2 仿真实验结果

图2 六自由度机械臂Fig.2 Six degrees of freedom manipulator

在SolidWorks平台中建立六自由度机械臂的模型，如图2所示。

利用SimMechainics插件导入到MATLAB/Simulink平台中。具体步骤：①在Mathworks官网下载对应版本的Simscape Multibody，共需下载两个文件，即smlink.r2014a.win64.zip和install_addon.m；②以管理员身份打开MATLAB，将所下文件所在路径添加到MATLAB当前文件夹下；③在命令栏输入install_addon(’smlink.r2014a.win64.zip’)；④提示成功后，继续输入regmatlabserver；⑤最后链接Solidworks，输入smlink_linksw命令。添加相应的运动驱动和传感模块，建立六自由度机械臂SimMechanics模型框如图3所示，能够看出机械臂各关节逐个串联起来。根据本文中所描述的无模型自适应滑模控制算法，在机械臂模型上搭建控制器Simulink模型。

图3 六自由度机械臂SimMechanics模型Fig.3 Six degrees of freedom manipulator SimMechanics model

设六自由度机械臂在运动过程中各关节期望角速度变化为：

(24)

在本研究中，分别采用无模型自适应控制方案(MFAC)和文中提出的无模型自适应滑模(Model-Free Adaptive Sliding Mode，简称MFSM)控制方案对机械臂各关节速度进行跟踪。

MFAC方案的输入输出初值、伪偏导数初值和控制器参数分别为y(k-1)=[0 0 0 0 0 0]T，y(k-2)=[0 0 0 0 0 0]T，u(k-1)=[0 0 0 0 0 0]T，u(k-2)=[0 0 0 0 0 0]T，Φ1=diag{[1 1 1 1 1 1]}，Φ2=diag{[1 1 1 1 1 1]}，ρ=0.3，η=0.7μ=λ=1。

MFSM方案的输入输出初值、伪偏导数初值及控制器参数分别为y(k-1)=[0 0 0 0 0 0]T，y(k-2)=[0 0 0 0 0 0]T，u(k-1)=[0 0 0 0 0 0]T，u(k-2)=[0 0 0 0 0 0]T，Φ1=diag{[1 1 1 1 1 1]}，Φ2=diag{[1 1 1 1 1 1]}，ρ=0.3，η=0.7，μ=λ=1，q=700，ε=5，γ=diag{[1 1 1 0.9 0.4 0.2]}。

为了更好地比较控制效果的差异，选取均方根误差为评价指标，两种控制方案的均方根误差如表1所示。

各关节的跟踪效果如图4所示。图4中Desired代表式(24)中对应的各关节期望速度，仿真时间为6 s。

从图4各关节跟踪效果中可以看出，无模型自适应控制(MFAC)和无模型自适应滑模控制(MFSM)两种方案都对各关节期望速度实现了跟踪，但是无模型自适应方法收敛太慢，在期望轨迹附近各关节均出现了不同程度的振荡。而本文设计的无模型自适应滑模控制器，控制效果明显优于MFAC。在MFAC控制方案下，关节1的超调量大，调节时间大于6 s；关节2的控制精度为±0.25 rad/s；关节3控制精度为±0.03 rad/s；关节4的轨迹沿着期望轨线来回穿梭，十分不稳定；关节5控制精度为±0.3 rad/s，初始阶段振荡频繁，响应慢，调节时间久；关节6初始超调量大，调节时间大于6 s。而基于MFSM控制算法的各关节跟踪效果，关节1超调为±0.17 rad/s，比MFAC表现要好很多，调节时间为0.1 s；关节2、3和4在期望轨迹振幅、频率不同的情况下均实现了精准的速度跟踪，控制精度均小于±0.01 rad/s，几乎与期望轨线重合；关节5响应快，超调量为0.2 rad/s，且不到0.2s的时间就到达稳态；关节6调节时间小于0.05 s，响应迅速，超调量几乎为零。从表1中两种控制方案的均方根误差可以看出，每个关节MFSM方案的均方根误差均要比MFAC的小很多。

通过分析可知，相比于现有的无模型自适应控制方法，本文设计的无模型自适应滑模控制器不依靠机械臂的精确模型，能够保证六自由度机械臂各关节对期望速度实现更快速、更加精确地跟踪效果。

表1 MFAC和MFSM的均方根误差Tab.1 Root mean square of errors from MFAC and MFSM

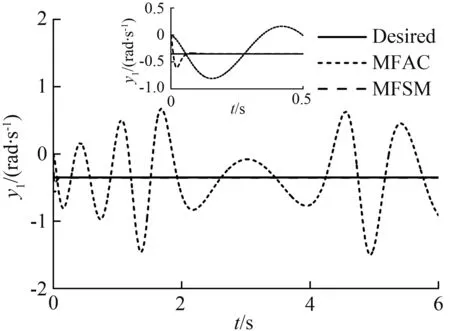
(a) 关节1速度跟踪

(b) 关节2速度跟踪

(c) 关节3速度跟踪

(d) 关节4速度跟踪

(e) 关节5速度跟踪

(f) 关节6速度跟踪

图4 各关节速度跟踪图
Fig.4 Each joint velocity tracking diagram

3 结语

本研究将无模型自适应滑模控制方案用于六自由度机械臂的速度跟踪控制。该方案将无模型自适应方法和滑模控制相结合，利用全格式动态线性化方法对机械臂模型进行动态线性化转换，从而把复杂时变的机械臂模型转换为简单易处理的“泛模型”，用滑模控制保证其收敛性，整个控制器的设计不需要模型的信息，只用到机械臂模型的输入输出数据。通过仿真实验结果表明，相比于现有无模型自适应方法，本文设计的无模型自适应滑模控制方法可以实现更迅速的响应、更精确的跟踪效果。