纳米梁非线性振动隧道电流反馈控制

(山东理工大学交通与车辆工程学院, 山东淄博255049)

0 引言

随着微纳米传感技术近几年的快速发展，纳机电系统(nano-electromechanical systems，简称NEMS)的振动控制研究已成为科研工作者关注的热点问题之一。作为重要的NEMS构件，纳米梁具有灵敏度高、轻质等特点，常被研究者用来制作高精度的传感器。但是随着尺寸的进一步减小，纳米梁在振动控制中容易出现多值、不稳定等的非线性特征，这严重影响了NEMS器件的稳定性。因此，消除振动控制中的非线性影响是纳微器件设计过程中首要考虑的问题，纳微器件的非线性振动控制成为微机电系统研究的一个重要方向。

近年来，传感技术得到了较快的发展，信号提取传感器的研究备受关注。电子隧道效应器件作为一种敏感性传感器，可以用于纳米梁的信号提取工作。Rockstad等[1]利用电子隧道效应原理制作了检测小位移的高性能加速度传感器。徐毓龙[2]介绍了基于量子隧道效应的器件和电路的优越性。罗源源等[3]设计了一种新型的基于隧道效应的微机械陀螺仪，把电子隧道原理应用到微机械振动陀螺的振动位移检测，其结构简单、功耗低、抗干扰能力强、可靠性好、线性度高，具有很高的灵敏度。Opacak等[4-5]研究了电子在复势垒中的隧穿现象，并得出共振频率表达式。李梦超等[6-7]研究了在隧道状态下低频纳米级振动对隧道间隙的影响，认为系统在隧道状态下对纳米级振动有很好的幅频响应。夏一等[8]基于量子隧道效应设计了用以测量纳米级微小测量量的隧道传感系统装置。

纳机电系统的非线性振动控制研究在近几年取得较大的进展。Dumitru等[9]研究了静电驱动悬臂梁微谐振器的非线性响应，并利用多尺度方法进行了分析。Shahrokh 等[10]研究了纳米梁非线性振动的控制方程，采用多尺度方法求得非线性控制方程的解析解，得到了纳米梁的非线性固有频率。Zhao等[11]建立了考虑表面效应的悬臂梁横向振动的力学模型，得到了纳米梁非线性振动方程的近似解析解。杨晓东等[12]考虑纳米梁的有限变形导致的几何非线性，得到系统的运动微分方程，应用多重尺度方法研究系统的非线性固有频率。刘灿昌等[13]以弹性理论为基础计算得到非局部效应和轴向非线性纳米梁的固有频率，研究了考虑非局部效应的纳米梁主谐波共振响应。Gong 等[14-16]针对纳米梁非线性振动控制问题提出了纳米梁非线性振动电容式传感器控制方法。Beni等[17]考虑卡西米尔力和弹性边界条件的影响，对梁式纳机电系统的静态不稳定性进行了理论研究。Wang等[18]研究了纳米梁在外载荷作用下的非线性共振问题，利用多尺度方法求出非线性控制方程，并讨论了频率和振幅之间的关系。Alves等[19]研究了矩形截面静电激励纳米梁的非线性动力学行为。

本研究基于隧道电流反馈控制的纳米梁非线性振动，将隧道效应理论应用于纳米梁非线性振动的信号提取中以增加信号提取的灵敏性与精确性。选用悬臂梁作为振动的物理模型，对基于隧道电流反馈控制的纳米梁非线性振动进行分析研究，利用隧道电流反馈提取振动信号，并推导出纳米梁主共振非线性振动方程，利用多尺度法推导出幅频响应方程并作出幅频响应图像，旨在研究直流和交流激励电压、振动控制参数、控制电压、阻尼等对系统主共振幅频响应的影响，以及分析有效控制非线性振动的影响因素。

1 隧道效应传感原理

根据量子力学理论，当两个电极之间的距离接近纳米量级尺度时，电子就可能穿越势垒，这种现象被称为隧道效应[20]。电子隧道器件作为一种具有极高灵敏度的位移换能器，已经被广泛用于信号检测与提取中。

在探测针与其对应表面之间的隧道电流值满足以下关系：

(1)

式中，κ为比例系数，V为偏置电压，β为转换因子，φ是势垒高度，z为两个导体面之间的距离。

由隧道效应产生的振动控制信号电压为：

(2)

式中，d为纳米梁与极板间的初始距离，w为纳米梁振动时的挠度，R为控制电路中的采样电阻。

2 纳米梁隧道电流反馈控制振动模型

图1 纳米梁隧道效应振动控制模型Fig.1 Vibration control model with tunnel effect of nanobeam

本研究选用一端固定、一端自由的悬臂纳米梁作为振动控制研究的动力学模型，如图1所示。AB和CD为两个控制极板，各连接一个控制器，分别对位移和速度电压进行反馈控制，EF为静电驱动极板，控制极板和驱动极板边界点A、B、C、D、E、F分别对应参数坐标值xA、xB、xC、xD、xE、xF，纳米梁与极板间的初始距离为d。在纳米梁左侧底部有一探测针，用于采集纳米梁振动信号。纳米梁长度方向的尺寸远大于其宽度和高度方向的尺寸。

基于隧道电流反馈控制，作用于纳米梁与静电驱动极板间的控制电压为：

Ucd=Uc+Uckw(xi,t)，

(3)

(4)

基于隧道电流反馈控制，作用于纳米梁与静电驱动极板间的激励电压为：

Uda=Ud+Uacos(Ω*t)，

(5)

式中，Ud是直流激励电压幅值，Ua是交流激励电压幅值，Ω*是激励信号频率。

作用于纳米梁与静电控制极板间的控制电压的平方为：

(6)

(7)

式中，g1为控制参数。

静电驱动力为：

(8)

静电控制力为：

(9)

式中，ε0是真空介电常数，W是纳米梁的宽度，d为纳米梁与极板间的初始距离，w为纳米梁振动的挠度，HAB、HCD和HEF满足Hij=[H(x-xi)-H(x-xj)]，H(x-xi)为阶跃函数。

在控制力作用下，基于隧道电流反馈控制的纳米梁非线性振动微分方程可表示为：

(10)

引入以下无量纲量：

(11)

式中，l表示纳米梁的长度。将式(5)～(9)和(11)代入式(10)中，对非线性项1/(1-u)2、1/(1+u)2进行泰勒级数展开。假设纳米梁振动系统是弱非线性系统，则系统参数可以用小参数变量ε表示，得到在控制力作用下基于隧道电流反馈控制的纳米梁无量纲非线性振动微分方程为：

(12)

3 纳米梁隧道电流反馈控制梁的非线性振动

本研究只考虑激励电压一阶谐波和静态部分对纳米梁非线性振动的影响，应用多尺度法求解方程(12)的近似解，并表示成以下形式[21]：

u(z,t,ε)=u0(z,T0,T1)+εu1(z,T0,T1)+…，

(13)

式中，ε是无量纲参数。

将式(13)及其对时间的导数带入式(12)，令方程等号左右两边ε同次幂的系数相等，得到以下偏微分方程：

(14)

(15)

本文中研究纳米梁主共振响应，取激励频率为：

Ω*=ωk+εσ，

(16)

式中，σ为频率调谐参数。

将式(14)的近似解用以下形式进行表示[22]，即：

(17)

(18)

将式(17)、(18)代入式(15)，进行模态正交化处理。为避免出现久期项，函数A应满足以下关系式：

(19)

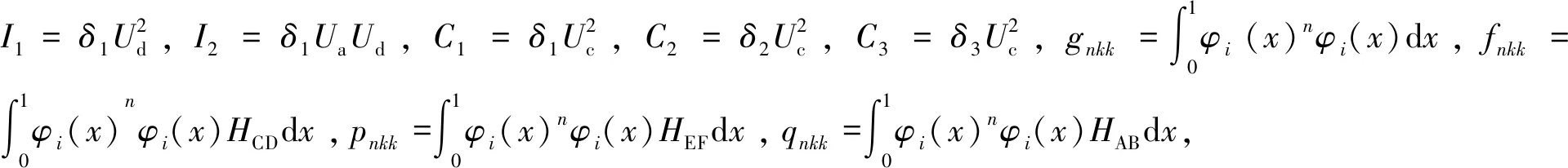
(20)

(21)

(22)

为确定纳米梁稳态振动时对应的振幅ak和相位γk，令D1ak=D1γk=0，即：

(23)

(24)

从而求得系统主共振的幅频响应方程和相频响应方程为：

(25)

(26)

对式(25)进行分析可得，幅频响应方程与激励电压、振动控制参数、调谐参数和纳米梁各参数值有关。

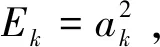
(27)

将式(27)对σ求导，令∂Ek/∂σ=0，且在共振频率点处满足：

vkEk+σk=0，

(28)

(29)

那么，可求得主共振的最大振幅akmax的两个解为：

(30)

分析式(30)可得知，主共振的峰值大小与非线性因素无关。

4 数值模拟与分析

本研究选用Euler-Bernoulli梁为振动模型，纳米梁的各参数值如表1所示。以一阶振动模态为例进行分析，得到基于隧道电流反馈控制的纳米梁非线性振动的幅频响应曲线图和相位图。

图2所示为直流激励电压不同时的振幅—频率关系曲线。由图2可得，当直流激励电压为2.5 V时，系统振动的最大振幅为0.56，振幅峰值点后出现多值区间，振幅随频率的变化呈非线性变化趋势，振动不稳定。当直流电压继续降至1.5 V时，最大振幅减小为0.28，且系统振动趋于稳定。随着直流激励电压幅值由2.5 V降为1.5 V，系统的振动幅度逐渐减小，衰减幅度为50 %，振幅峰值点处频率逐渐趋于共振频率。由此可得，减小电路中的直流激励电压值可以使系统振动的非线性减弱甚至消失。

图3所示为交流激励电压不同时的振幅—频率关系曲线。当交流激励电压为2.0 V时，系统振动不稳定，最大振幅为0.55，最大振幅处的频率点向右偏离共振频率点，振幅峰值点之后开始出现多值区间，系统振动表现为非线性振动。当交流电压降为1.0 V时，最大振幅削减为0.23，系统的非线性减弱。随着交流电压由2.0 V减小至1.0 V，系统的振动幅度随之减小，衰减幅度为58 %，振幅峰值点向右偏离共振频率点的距离减小，系统振动趋于稳定状态。由此可得，降低交流激励电压幅值可以减弱甚至消除系统的非线性。

表1 纳米梁振动模型各参数值Tab.1 Parameters of the nanobeam vibration model

图2 不同直流激励电压下的振幅—频率关系曲线
Fig.2 Relationship curves of amplitude-frequency withdifferent direct current excitation voltages

图3 不同交流激励电压下的振幅—频率关系曲线
Fig.3 Relationship curves of amplitude-frequency withdifferent alternating current excitation voltages

图4所示为阻尼不同时的振幅—频率关系曲线。当阻尼值为0.021时，系统最大振幅为0.56，最大振幅点向右偏离共振频率点，存在多值区间，振动不稳定。当阻尼值继续增大至0.028时，系统的最大振幅减小至0.36，系统的非线性减弱，振动趋于稳定。当直流、交流激励电压幅值和其他参数值一定时，系统的振幅峰值随阻尼系数的增大而减小，衰减幅度为36 %，振幅峰值点向右偏离共振频率点的距离也随之减小，系统的振动由不稳定非线性振动趋于稳定振动状态。由此可得，增大阻尼值可以减弱系统振动的非线性。

图5所示为纳米梁与极板间的初始距离不同时的振幅—频率关系曲线。当纳米梁与极板间的初始距离为480 nm时，在共振点的右侧，振动出现多值区间，振幅峰值点向右偏离共振频率点，出现明显的非线性振动现象。当纳米梁与极板间的初始距离增加为520 nm时，系统的振幅峰值减小，系统振动的非线性明显减小但仍然存在。当纳米梁与极板间的距离为560 nm时，系统的最大振幅减小至0.34，振动逐渐趋于稳定状态。当激励电压幅值与其他参数值一定的情况下，随着纳米梁与极板间初始距离的增加，系统的最大振幅逐渐减小，衰减幅度为54 %，振幅峰值点向右偏离共振频率点的距离减小，系统的振动逐渐由不稳定状态趋于稳定状态。由此可得，增大纳米梁与极板间的初始距离可以减弱系统非线性。

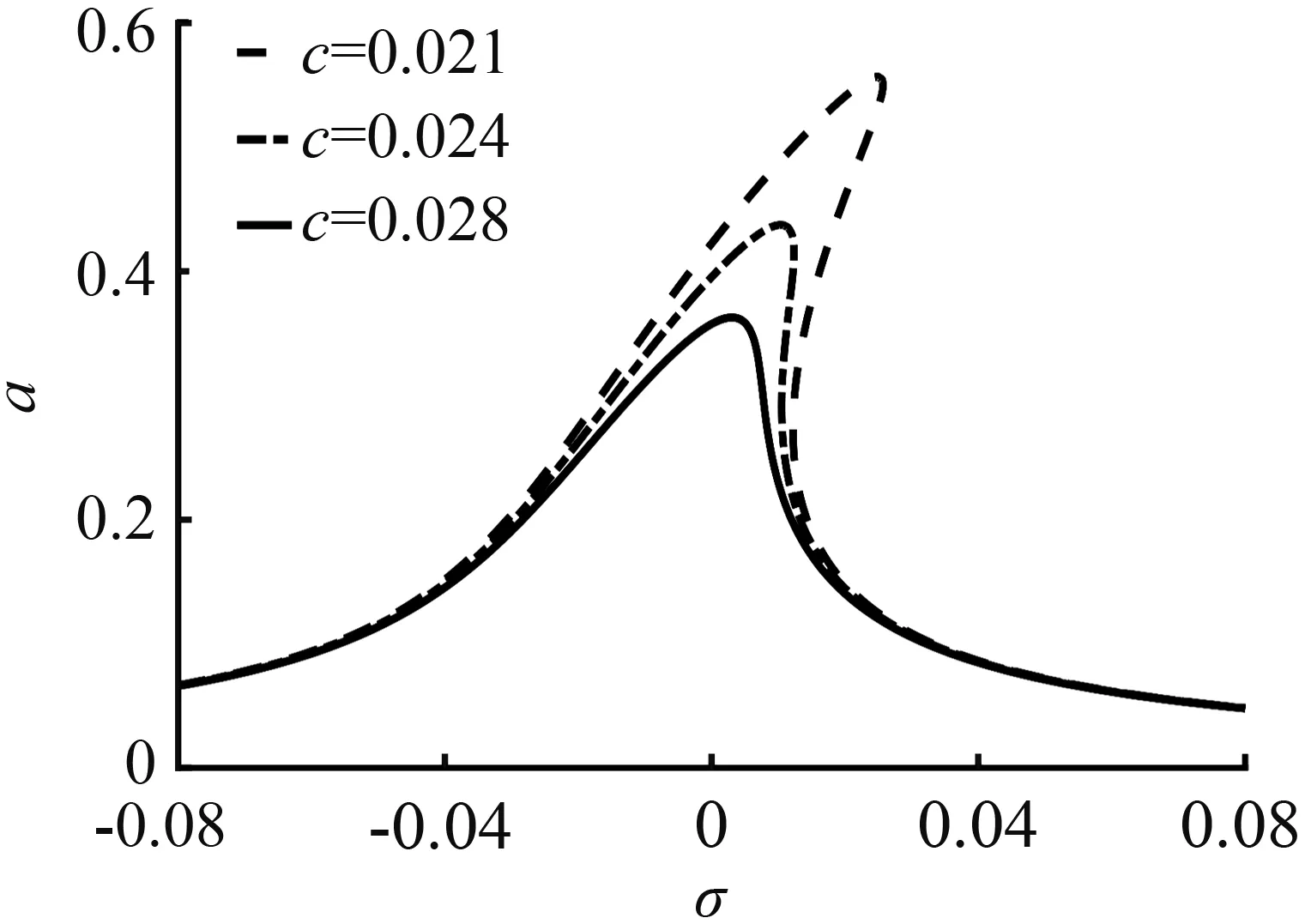
图4 不同阻尼下的振幅—频率关系曲线
Fig.4 Relationship curves of amplitude-frequencywith different damping

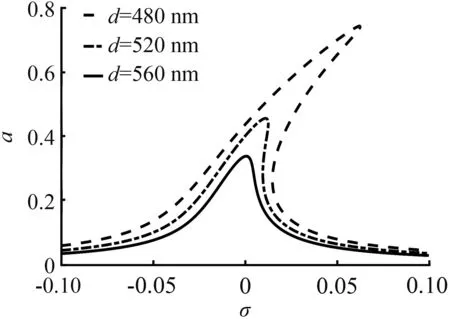
图5 不同的纳米梁与极板间初始距离下的振幅—频率关系曲线
Fig.5 Relationship curves of amplitude-frequencywith different initial distance betweenthe nanobeam and the plate

图6所示为控制电压不同时的幅频响应曲线。分析图6可得，改变系统的控制电压对振幅的大小无明显影响，系统的振幅峰值基本保持在0.56左右。当控制电压为6.0 V时，振幅峰值点明显向右偏离共振频率点，出现多值区间，系统振动不稳定。随着控制电压由6.0 V降为2.0 V时，振幅峰值大小基本没发生改变，振幅峰值点向右偏离共振频率点的距离减小，系统的振动逐渐趋于稳定状态。由此可得，减小系统控制电压可以减弱系统振动的非线性。

图7所示为阻尼不同时最大振幅随纳米梁长度变化曲线。当保持阻尼值一定时，最大振幅akmax随纳米梁长度的增加而增大。当纳米梁的长度一定时，阻尼值越大，最大振幅akmax的值越小。这与图4所示的阻尼不同时的幅频响应曲线所得结论相对应，也与式(30)所得出的结论相一致。

图6 不同控制电压下的振幅—频率关系曲线
Fig.6 Relationship curves of amplitude-frequencywith different control voltages

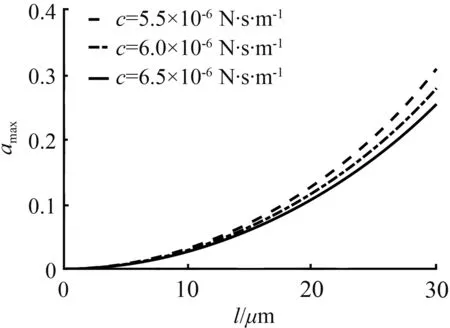
图7 阻尼不同时最大振幅随纳米梁长度变化曲线
Fig.7 Curves of the maximum amplitude varyingwith nanobeam length under different damping

图8和图9分别为控制增益和控制电压不同时非线性项随纳米梁长度变化曲线。非线性项vk能够影响系统振动的稳定性，将vk控制在合理的范围内可以减小系统振动时的非线性。当纳米梁的控制增益参数一定时，非线性项vk随纳米梁长度的增加而逐渐减小。当纳米梁的长度一定时，非线性项vk随振动控制增益参数和系统控制电压的增大而减小。由此可得，选择合适的控制增益参数和控制电压可以将非线性项vk控制在合理范围内，对纳米梁非线性振动进行控制与调节，从而增加系统的稳定性。

图8 控制增益不同时非线性项随纳米梁长度变化曲线
Fig.8 Curves of the nonlinear term varyingwith nanobeam length under differentcontrol gain parameters

图9 控制电压不同时非线性项随纳米梁长度变化曲线
Fig.9 Curves of the nonlinear term varying withnanobeam length for different control voltages

分析图2～图6的振幅—频率关系曲线可得，适当改变直流和交流激励电压、控制电压、阻尼值、纳米梁与极板间的初始距离可对纳米梁主共振幅频响应产生一定的影响，同时可以对系统振动非线性进行调节与控制。当直流激励电压由2.5 V减小为1.5 V，交流激励电压由2.0 V降低为1.0 V时，系统的振幅峰值减小，振幅衰减幅度分别为50 %和58 %，振动非线性减弱，振动由不稳定状态趋于稳定状态；当系统的阻尼值不断增加至0.028时，系统的最大振幅减小，衰减幅度为36 %；当增加纳米梁与极板间的初始距离至560 nm时，振幅峰值减小，衰减幅度为54 %，系统非线性减弱；系统控制电压对振幅峰值没有明显的影响，但减小控制电压，可以明显减弱振动非线性。

图7通过描述阻尼不同时最大振幅随纳米梁长度的变化验证了图4所得出的结论，验证了在振幅—频率关系曲线中得出的增大阻尼值可以明显减小振幅峰值结论的正确性。图8和图9分别通过改变振动控制增益参数和控制电压分析了两者的改变对非线性项的影响，选择合适的振动控制增益参数和控制电压可以将非线性项控制在合理范围内，从而使振动非线性得到有效的控制。

与传统的信号提取装置相比，将隧道电流反馈应用于振动信号提取过程中可提高了信号检测的灵敏性与准确性。从对振动非线性的控制结果看，隧道电流反馈控制能明显减小纳米梁的振幅峰值，对系统振动非线性有明显的控制与调节作用。

5 结论

①在隧道电流反馈控制作用下，适当减小直流或交流激励电压幅值、增大阻尼、增大纳米梁与极板间的初始距离可以减小系统的振动幅值。

②直流和交流激励电压、控制电压、阻尼值、振动控制增益参数、纳米梁与极板间的初始距离是系统非线性振动的影响因素，通过适当减小直流和交流激励电压幅值、增大阻尼、增大纳米梁与极板间的初始距离、减小控制电压、选择适当的控制增益可以降低纳米梁振动的非线性，提高系统稳定性。

③基于隧道电流反馈控制，通过选取合适的控制电压和控制增益可以将系统的振动非线性项控制在合理范围内，从而实现对纳米梁非线性振动的控制。