一种新型六自由度可重构并联机构的奇异性分析
2蔡敢为
(1.广西大学机械工程学院, 广西南宁530004;2.柳州铁道职业技术学院汽车技术学院, 广西柳州545616)
0 引言
当并联机构处于奇异位形时,机构的雅可比矩阵行列式的值为零或雅可比矩阵的秩不为满秩,导致机构无法有效地在该位形下传递动力与运动,使得机构处于失常状态,所以对并联机构进行奇异位形的研究是学者们广泛讨论的热点,并取得了较好的研究成果。Lu等[1-3]对一种2R1T型的3-UPU并联机构用雅可比矩阵法分析其奇异性;吴鑫等[4]对2T1R并联机构进行了位置及奇异性分析;Qin等[5]对2U+UPS非对称并联机构进行了构态与驱动分析;Gan等[6-7]对一种2T2R型的2RPS-2UPS的并联机构进行了奇异性分析;YE等[8]分析了一类支链可重构并联机构的动态变化过程;吴金波等[9]分析了一种1T2R的3-UPU并联机构奇异性;Xu等[10]设计了一种多级有序可展并联机构并对其进行了分析;柴馨雪等[11]根据2-UPR-RPU并联机构的雅可比矩阵求出了该机构的三类运动学奇异位形;杜晴晴等[12]利用3-PRRS六自由度并联机构速度的输入输出关系分析了该机构的边界奇异并推导出位形奇异轨迹的解析式;殷开明等[13]根据4-SPS/SP并联机构的运动学和动力学分析结果得到了该机构的降维运动学和静力学奇异位形曲线并进行分析;曹永刚等[14]寻找到了一种间接表征6-RSS型并联机构奇异位形空间分布的方法;刘知辉等[15]定义了雅克比矩阵转置矩阵的∞-范数的指标来求取并分析了3-CRR型并联机构的奇异性。
从以上研究成果可看出,极少学者对三分支类型的并联机构进行奇异性分析,尤其是奇异轨迹的分析,目前尚未见到对三分支且各分支类型可相互转换的六自由度可重构并联机构进行奇异性分析。因此,本文以新型六自由度可重构并联机构为研究对象,先建立机构的位置反解方程,然后对其求导,最后分别对其雅可比矩阵行列式进行讨论,以得到机构在奇异时的奇异轨迹与奇异位形。
1 机构的运动学反解
本研究工作以一种新型六自由度可重构并联机构为研究对象,对其进行奇异性分析。该机构的三条分支均由一长杆和一滚珠丝杠组成,当三条分支的长杆与滚珠丝杠分别平行时,滚珠丝杠滑块滑动,机构为3-SPS结构,此为构型一;当任意两条分支的长杆与滚珠丝杠分别平行,其余一条分支的滚珠丝杠滑块固定在末端位置,且其长杆相对滑块转动时,该机构为2-SPS-SRS结构,此为构型二;当任意两条分支的滚珠丝杠滑块固定在末端位置,长杆分别相对滑块转动,其余一条分支的长杆相对滚珠丝杠平行时,该机构为2-SRS-SPS结构,此为构型三;当三条分支的滚珠丝杠滑块均固定于末端位置,长杆相对丝杠滑块转动时,该机构为3-SRS结构,此为构型四。图1所示为4种构型转换示意图。

(a) 3-SPS(b) 2-SPS-SRS(c) 2-SRS-SPS (d) 3-SRS
分别在SPS分支与SRS分支上建立机构分支的局部坐标系Oij-XijYijZij(i=1,2,3;j=1,2,3,4),其中,i表示第i分支,j表示分支中第j个转动副轴线,该坐标建立在各个转动副轴线的交点上,Zij为转动副轴线方向,Xi1的方向垂直于Zi1与Zi2,Xi2的方向垂直于Zi2与Zi3,Xi3的方向垂直于Zi3与Zi4,θi1为Xi0与Xi1的夹角,θi2为Xi1与Xi2的夹角,θi3为Xi2与Xi3的夹角,θi4为BiCi与Xi4的夹角;在动平台建立动坐标系O5-X5Y5Z5,其中,X指向驱动电机方向,Z垂直于动平台,则Y的方向由由右手定则判定;在定平台建立基坐标系O-XYZ,其中,X指向驱动电机方向,Z垂直于基座,则Y的方向由由右手定则判定。定平台的等边三角形外接圆半径为R,动平台的正三角形外接圆半径为r,其中,Ai(i=1,2,3)分别为与定平台相连的各个复合球铰的中心点,Bi(i=1,2,3)分别为各个分支中间转动副的中心点,Ci(i=1,2,3)分别为与动平台相连的复合球铰的中心点。坐标系的建立分别如图2、图3和图4所示。其中,当分支为SPS时(如图2所示),Li为分支的移动副移动距离,当分支为SRS时(如图3所示),li1与li2分别为连杆一的长度与连杆二的长度。

图2 SPS分支坐标系建立
Fig.2 SPS branch coordinate system established

图3 SRS分支坐标系建立
Fig.3 SRS branch coordinate system established

图4 总体坐标系建立Fig.4 Overall coordinate system is established
动平台上任意一点相对于定平台的位姿矩阵[16]为:
(1)
动平台在定平台上的坐标转换表达式为:
S=TS′,
(2)
因此,可求得分支为SPS时的位置反解参数θi1与Li分别为:
(3)

分支为SRS时,反解参数θi1、θi2与θi4的约束方程可表示为:
(4)
其中,Aij(i=1,2,3;j=1,2,3)为关于机构本身的尺寸与位姿参数,sij=sinθij,cij=cosθij,j=1,2,3。
通过结式消元法,式(4)可化为:
(5)

通过对式(5)的求解便可求出分支为SRS时的所有反解参数。
2 机构雅可比矩阵的建立
对机构的SPS分支的位置反解方程进行求导,可得:
(6)
对机构的SRS分支的位置反解方程进行求导,可得:
(7)
将以上对各分支位置反解方程求导所得的方程进行组合,即可得到机构的任意构型下的雅可比矩阵,可统一表示为:
(8)

除了3-SPS构型的输出雅可比矩阵J1为方阵以外,其他构型的输出雅可比矩阵J1都不为方阵,所有构型的输入雅可比矩阵J2都为方阵。
3 机构的逆向奇异分析
逆向奇异是对雅可比矩阵J2进行分析。由于所有的J2均为方阵,所以可直接用雅可比法对其行列式进行直接求解。
当机构支链类型为SPS时,令det(J2)=0,可得:
-2Li[(ki1cηi+ki2sηi)si1+ki3ci1]=0,
(9)

图5 Ci奇异时的运动轨迹Fig.5 Ci singular trajectory
此时可分三种情形讨论。
情形一:由于Li为连杆二相对连杆一的滑动长度,即AiCi的长度,其不可能为零,因此可排除。
情形二: 当θi1=0与ki3=0时,有det(J2)=0,在物理意义上为Ci点在Z=0的平面上,但是当θi1=0时,只有当θi2=0或θi2=-π时,Ci点才可能在Z=0的平面上,θi1与θi2不能同时满足上述角度关系,这种情形可以排除。
当θi1=±π/2和ki1cηi+ki2sηi=0时,也有det(J2)=0,此时Ci点在如图5所示的直线上运动,机构处于逆向奇异。
此时SPS分支对应的位姿关系如图6所示。

(a) i=1时的位姿关系图 (b) i=2时的位姿关系图 (c) i=3时的位姿关系图
情形三:如果{θi1<|π/2|}∪{θi1≠0},有:
(10)
结合式(3)可推出:
(11)
式(11)明显不成立,因此,此情形可排除。
当机构支链类型为SRS时,令det(J2)=0,有:
(12)
其中,Hi(i=1~6)为与θi1、θi2、Ai1、Ai2、Ai3相关的参数,并且存在如式(13)的关系,即:
(13)
此时同样可分三种情形讨论。
情形一:当θi2=0或θi2=-π时,由式(12)可得det(J2)=0,此时连杆AiBi与Z=0位于同一平面上。

情形三:当-π<θi2<0时,可分四种情况讨论。
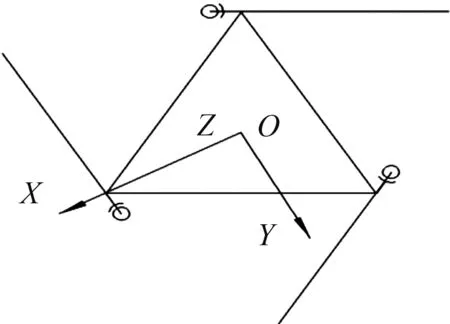
图7 Ci奇异时的运动轨迹Fig.7 Ci singular trajectory
情况1:当θi1=0时,如果Ai3=0则可推出det(J2)=0,此时在物理意义上可得Ci点位于Z=0的平面上时,机构才处于边界奇异。但是当θi1=0时,只有θi2=0或θi2=-π时,才可得到Ci点位于Z=0的平面上这一结论,这与-π<θi2<0所给区间并不符合,因此可排除。

此时SRS分支对应的位姿关系如图8所示。

(a) i=1时的位姿关系图 (b) i=2时的位姿关系图 (c) i=3时的位姿关系图
情况3:如果Ai2与Ai3同时为零时,也可得到det(J2)=0,这种情况与情形二的结论一样,此时该分支对应的位姿关系如图9所示。

(a) i=1时的位姿关系图 (b) i=2时的位姿关系图 (c) i=3时的位姿关系图
情况4:如果Ai1与Ai2与Ai3的值都等于零,也可推出det(J2)=0,此时Ci点与Ai点重合在一起,此种情况只有当AiBi杆与BiCi杆相互重合时才会发生,因此,只要保证两杆在运动中不重合在一起,则该情况可排除。
综上所述,机构分支在运动过程中处于边界奇异的位形图,如图10所示。

(d) SRS结构Ai2与Ai3同时为零的边界位形
图10 机构分支边界奇异图
Fig.10 Institutional branch boundary singularity
4 机构的正向奇异分析
机构正向奇异是对雅可比矩阵J1进行分析,当det(J1)=0时,在物理意义上,当机构处于正向运动学奇异时,即使锁住所有的驱动电机,动平台依然会存在一个不可控制的运动,即多出了一个自由度。因为该机构只有在构型一时其雅可比矩阵J1为方阵,因此,可直接采取雅可比法进行求解,但是对于构型二、构型三和构型四来说,其雅可比矩阵并不为方阵,当并联机构动平台上3个点的速度法平面的交点落在该三点所组成的平面上时,即使将所有驱动副刚化,动平台也会存在一个不可控制的自由度。所以这里对构型一采用雅可比法分析,对构型二、构型三、构型四采取机构奇异定理分析。
当机构为构型一时,令det(J1)=0,可得:
f(θi1,α,β,γ,X,Y,Z)=0,
(14)
将SPS分支的运动学反解式(3)代入到式(14)当中,可得:
f(α,β,γ,X,Y,Z)=0,
(15)

图11 构型一在(0,0,0)下的奇异轨迹Fig.11 A singular trajectory under (0,0,0)
构型一在姿态角为(0,0,0)时的奇异轨迹如图11所示。
下面采用机构运动的奇异定理建立构型二、构型三与构型四的正向奇异判别方程。首先对SPS分支进行分析,当锁住SPS分支上的驱动副Li与θi1时,如果Ci点仍可运动,速度vi方向应与AiCi方向垂直,则Ci点速度法平面的方向向量就为Ci点的速度方向向量,如图12(a)所示。当分支为SRS类型时,如果锁住驱动副θi1、θi2与θi4,如果Ci点仍可运动,速度vi方向应与AiBiCi平面相垂直,则Ci点速度法平面就为AiBiCi平面,如图12(b)所示。

(a) SPS分支速度方向

(b) SRS分支速度方向
图12 分支速度方向图
Fig.12 Branch speed pattern
当分支为SPS时的速度法平面方程为:
Ei2x+Bi2y+Ci2z+Di2=0,
(16)
其中:
Ei2=-ki2Ci1-ki2Di1+ki3Bi1,
Bi2=-Ai1ki3+ki1Ci1+ki1Di1,
Ci2=-ki1Bi1+Ai1ki2,
Di2=-Cix(-ki2Ci1-ki2Di1+ki3Bi1)+Ciy(Ai1ki3-ki1Ci1-ki1Di1)-Ciz(-ki1Bi1+Ai1ki2),
式中,Ei1、Bi1、Ci1、Di1分别为平面AiCiDi方程中的参数,Cix、Ciy、Ciz分别为Ci点的坐标。
当分支为SRS时的速度法平面方程为:
Ej3x+Bj3y+Cj3z+Dj3=0,
(17)
其中:
Ej3=acηiBiz-acηiCi3+RsηiBiz+CizBiy-CizBiz-RsηiCiz,
Bj3=-asηiCiz+RcηiCiz+asηiBiz-RcηiBiz-BixCiz+CixBiz,
Cj3=CixsηiR+asηiCiy+RcηiBiy-aBixcηi-RcηiCiy+aCixcηi-RBixsηi-CixBiy-asηiBiy+BixCiy,
Dj3=aBixcηiCiz-asηiCiyBiz-RCixsηiBiz+asηiCizBiy-RcηiCizBiy+RcηiCiyBiz-
aCixcηiBiz+RBixsηiCiz,
式中,Bix、Biy、Biz分别为Bi点的坐标,Cix、Ciy、Ciz分别为Ci点的坐标,R、a、r、li1、li2分别为机构尺度参数,sij、cij(j=1,2)分别为分支转角参数。


图13 构型二、三、四的奇异轨迹
Fig.13 Two, three, four singular trajectories
5 结论
①对新型六自由度可重构并联机构进行了运动学反解数学模型的建立,并对机构的运动学反解方程进行求导,得到了机构在各构型下的正、逆雅可比矩阵。
②通过分析机构的逆向雅可比矩阵的行列式,对各个构型的逆向雅可比矩阵进行求解,得到了机构处于边界奇异下的分支位形与位姿关系图。
③对构型一用雅可比矩阵法求出了正向奇异的奇异轨迹,对构型二、构型三和构型四采用机构的运动奇异原理求出了其奇异轨迹,并将它们进行对比分析,为以后该机构的工作空间、动力学分析等提供了理论参考。

