阿克曼转向误差对前驱车转向回正性的影响

(山东理工大学交通与车辆工程学院， 山东淄博255091)

0 引言

四轮汽车在低速转向时的横向加速度很小，可忽略不计，轮胎处于自由状态，转向中心位于后车轴的延长线上，为此转向系统被设成满足阿克曼转向几何条件[1]。但阿克曼转向所依赖的双轴汽车模型是平面车辆模型，其双轴、四轮和质心都在平面上，简化为单轨模型时轮荷变化也会被忽略。但大量研究和实验表明，汽车实际的转向几何关系介于平行转向和阿克曼转向之间，尤其在低速转角条件下，其转向梯形所引起的阿克曼转向误差可造成实际内外轮转角差角远小于理想的阿克曼转向，使得前后轮转向中心不通过同一点而彼此干涉[2-3]。阿克曼转向误差人为设置主要考虑到汽车在较高速度转向时离心力会导致载荷转移现象，此时内轮的影响不再那么重要，为了充分利用具有较大轮载的外轮附着力以保持高速稳定性，外侧车轮侧偏角应该更大，可行的解决方法是后轮负前束或阿克曼转向误差，而作为非驱动轮后轮，在四轮定位中，为保证推力线位于几何中心线上并减小转弯半径，一般会设置后轮前束，则人为设置阿克曼转向误差成为必然，但如果阿克曼转向误差设置不当，汽车转向盘在接近极限位置还会出现回正困难，甚至产生回正阻力矩。对国产雷丁某款改装电动车的实验研究也发现，一些前驱电动车在低速匀速转向过程中，当转向盘转到极限位置回复一定角度时，转向盘会存在向极限位置运动倾向，这与阿克曼转向误差和阿克曼转向引起的左右轮驱动回转力矩不平衡密切相关。

目前在研究低速问题时大多只考虑小角度转向情况，对低速大转角研究较少，也未考虑载荷转移和定位参数的影响，所建立的2自由度模型并不能很好地解决低速大转角问题。本研究针对低速大转角转向回正性差的，考虑载荷转移和定位参数变化的影响因素和基于轮胎刷子模型的纵滑侧偏工况，建立了簧上4自由度整车模型，以分析低速大转角时阿克曼转向误差对驱动力、侧向力及回正性能的影响，并进一步指导阿克曼转向梯形的优化，使得汽车转向更加具有可控性。

1 模型建立

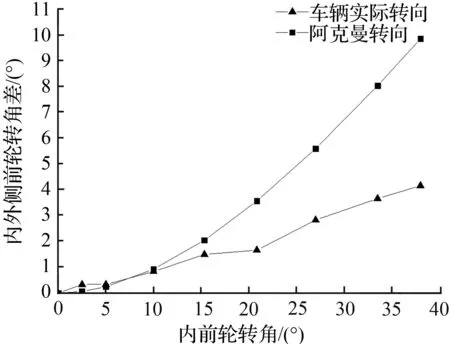
图1 内外侧前轮转角差随内前轮转角的变化Fig.1 Corner angle difference of inner-front and outer-front wheel with inner-front wheel corner angle

1.1 阿克曼转向误差率定义

本文以雷丁某款前驱电动车为研究对象，研究阿克曼转向误差对转向性能的影响，其内外轮转角关系的如图1所示[4]。实验车辆采用无助力形式，并引入阿克曼转向误差率，假设外轮最大转角一定，则阿克曼转向误差率可以表示为：

(1)

式中，εO为阿克曼转向误差率；δ1为内轮转角(°)；δ2为外轮转角(°)；K为两主销接地点距离(m)；L汽车轴距(m)。

1.2 整车模型

对于平面大转角运动的车辆，相对于固定于地面的坐标系，车辆的纵向和侧向是持续变化的。为了分析方便，本文中假设：

①把转向梯形对转角的影响统一到阿克曼转向误差对转向性能的影响。

②不考虑轮胎宽度。

③不考虑悬架变形转向，即认为左右主销轴线相对位置保持不变，主销接地点相对位置不变[5]。

④汽车质量左右对称分布。

⑤假设所有车轮初始前束和外倾为零。

为了进一步分析阿克曼转向误差的影响，建立基于地面O的固定于地面的平面坐标系X0-Y0，以及固定于簧载质心S处车辆坐标系x0-y0，同时，在S点建立X轴始终指向速度方向的坐标系X-Y，如图2所示。

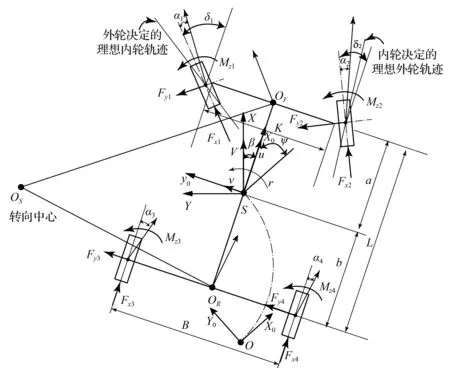
图2 低速大转角前驱车运动模型Fig.2 Motion model of low-speed large-angle front-drive vehicle

图2中，运动的x0轴相对于静止的X0轴的航向角为ψ，而绕侧倾轴的侧倾角为φ，X-Y坐标系与x0-y0坐标系具有相同的原点，区别在于x0指向车身纵向速度方向，而X指向车辆速度方向，S为簧载质心。图中所示出的各运动量和力均代表了在该坐标系中的正方向，则坐标系中的变量满足式(2)，即：

(2)

式中，u、v、r分别为车身质心纵向速度、侧向速度及横摆角速度。

在车辆坐标系x0-y0中，车辆质心处合外力满足式(3)，即：

(3)

式中，i=1、2、3、4代表内前轮、外前轮、内后轮和外后轮；δi表示各轮转角(°)；Fxi为各轮的纵向力(kN)；Fyi分别表示各轮侧向力(kN)。

考虑侧倾对轮荷的影响时需要簧载质心位置、侧倾力臂和侧倾轴等参数，各参数取值见表1。无侧倾时汽车侧向示意图如图3所示。其中，hRC为车辆质心的垂线与侧倾轴的交点P点离地高度，θ为簧载质心位置侧倾轴倾斜角，hCG为簧载质心高度，hs为侧倾力臂长度。

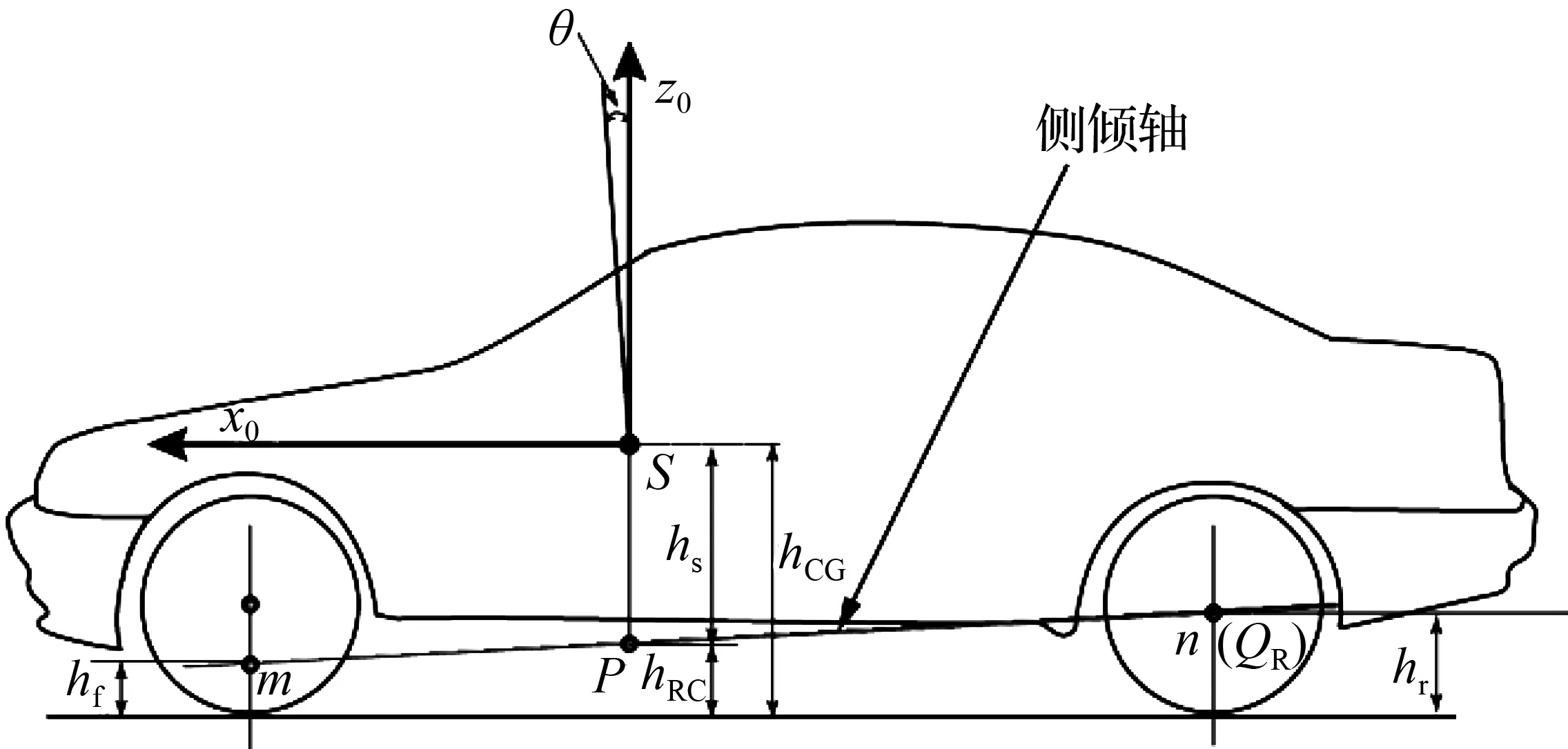
图3 无侧倾时汽车侧向图Fig.3 Vehicle side view without roll

不考虑车身上下运动、侧倾和俯仰瞬时运动对转向性能的影响[6]，根据质心运动定理，则汽车低速转向时平移运动、侧倾运动、俯仰运动和横摆运动的力矩关系如式(4)～(7)所示，即：

(4)

(5)

(6)

(7)

式中，ms簧载质量(kg)；hf、hr分别为前、后侧倾中心离地距离(m)。

若将模型各分量换算到X-Y坐标系下，可得：

(8)

进一步求得平衡方程：

(9)

(10)

(11)

∑N=0，

(12)

式中，V为车速(m/s)；R转弯半径(m)；β为质心侧偏角(°)；∑FX为质心轨迹切线方向合外力(kN)；∑FY为质心法线方向合外力(kN)。

2 模型参数计算

2.1 质心侧偏角、横摆角速度和侧倾角计算

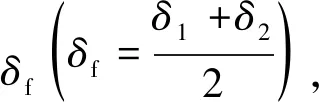
mVr=(kf1+kf2)αf+(kr1+kr2)φαr，

(13)

(kf1+kf2)αfa-(kr1+kr2)αrb=0，

(14)

式中，kf=kf1=kf2、kr=kr1=kr2，且αf、αr满足以下关系：

(15)

(16)

则可得质心侧偏角β和横摆角速度r分别为：

(17)

(18)

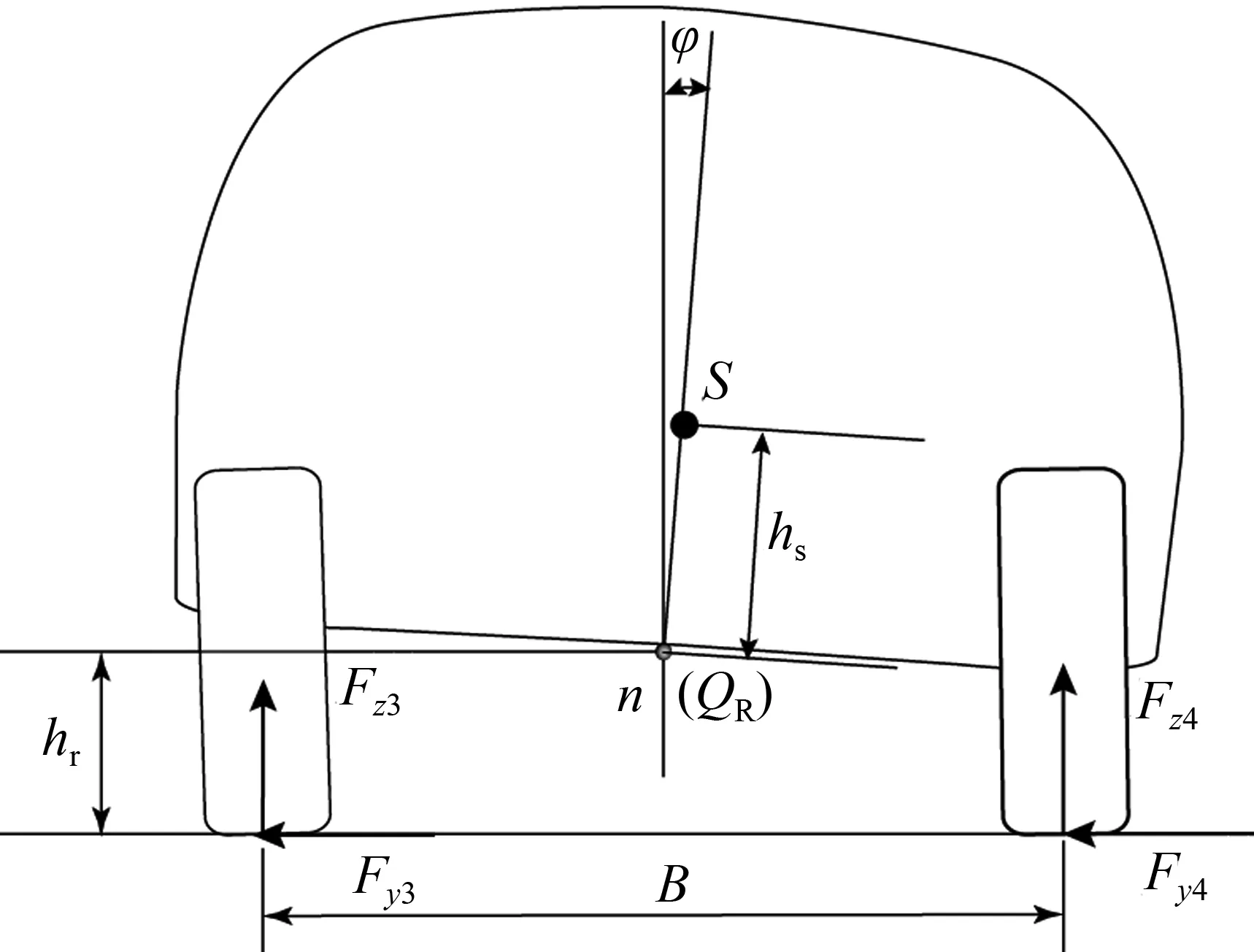
图4 侧倾运动示意图Fig.4 Schematic diagram of the roll motion

由簧载质心S上作用离心力产生的绕瞬时轴线的力矩，以及车身绕瞬时轴线转动质心的侧向位移产生侧倾角φ(如图4所示)共同形成的侧倾力矩Mφ为：

(19)

该力矩需要通过车身弹簧由车轴产生的力矩平衡，因此有：

Mφ=(kφf+kφr+ksa)φ，

(20)

图4中，OR为侧倾轴线与后轴线交点，S为簧载质心，hr后侧倾中心离地距离，由式(19)和式(20)可解得侧倾角为：

(21)

式中，kφf、kφr为前后轴侧倾刚度(N·m /rad)。其中，kφ=kφf+kφr；ksa为横向稳定杆侧倾刚度(N·m /rad)。

2.2 各轮垂直载荷计算

假定只有前横向稳定杆且前后轴没有载荷转移，则前后轴左右轮载荷转移量为：

(22)

(23)

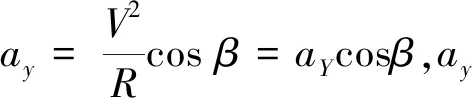
侧向载荷转移后的各轮垂直载荷分别为[7]:

Fz1=Fz10-ΔFzf，

(24)

Fz2=Fz20+ΔFzf，

(25)

Fz3=Fz30-ΔFzr，

(26)

Fz4=Fz40+ΔFzr，

(27)

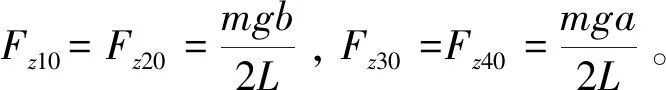
2.3 侧偏角计算

轮胎侧偏角与转角满足以下关系[8]：

(28)

(29)

(30)

(31)

式中，δ1、δ2、δ3、δ4为各车轮转角(°)。

2.4 附加力矩计算

式(7)中∑Mz0i是各轮附加力矩Mzi作用在车辆质心处合力矩，即：

∑Mz0i=∑Mzi，

(32)

式中，附加力矩Mzi是各轮自回正力矩、外倾侧向力回正力矩、驱动力回正力矩以及侧向力回正力矩之和的反作用力矩(N·m)。

3 示例计算

附加力矩的计算需要主销后倾距和主销偏移距等初始定位参数，主要计算参数及其取值如表1所示。

表1 主要计算参数及取值
Tab.1 Main calculation parameters and values

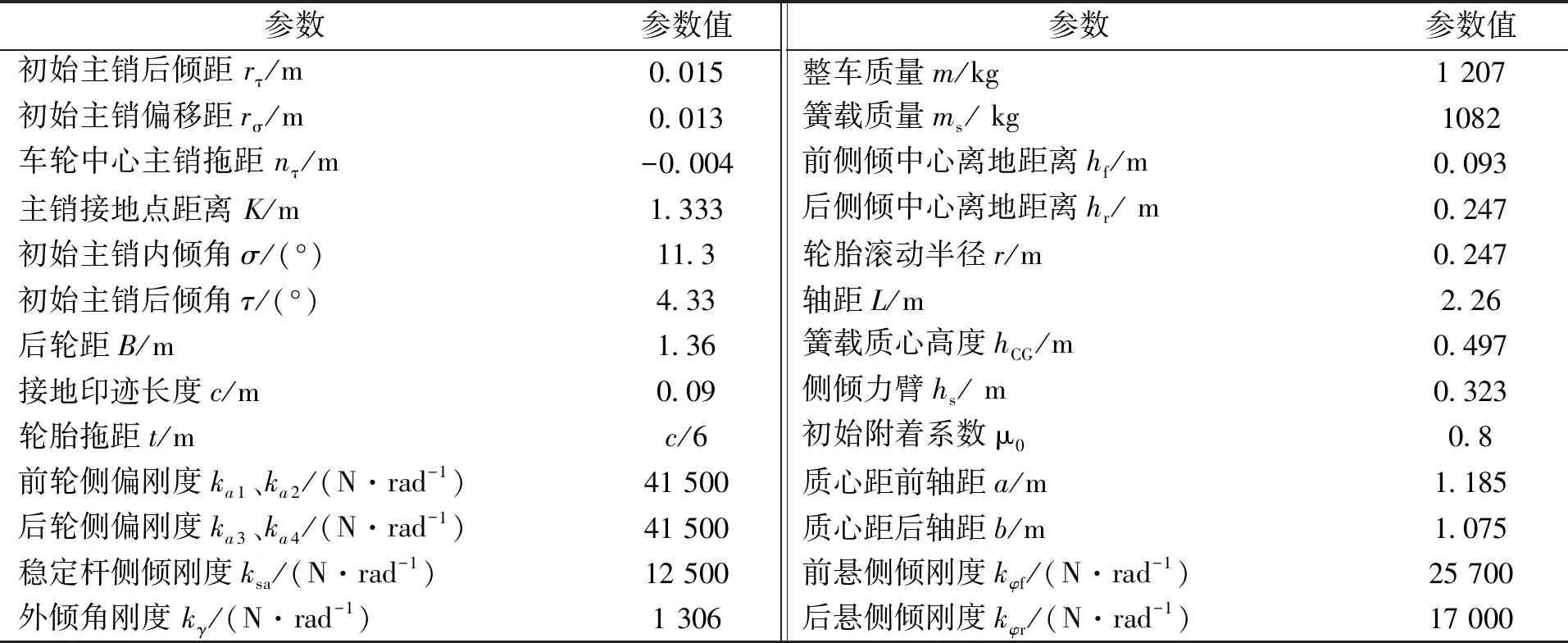
参数参数值参数参数值初始主销后倾距 rτ/m0.015整车质量m/kg1 207初始主销偏移距rσ/m0.013簧载质量ms/ kg1082车轮中心主销拖距 nτ/m-0.004前侧倾中心离地距离hf/m0.093主销接地点距离 K/m1.333后侧倾中心离地距离hr/ m0.247初始主销内倾角σ/(°)11.3轮胎滚动半径r/m0.247初始主销后倾角τ/(°)4.33轴距L/m2.26后轮距B/m1.36簧载质心高度hCG/m0.497接地印迹长度c/m0.09侧倾力臂hs/ m0.323轮胎拖距t/mc/6初始附着系数μ00.8前轮侧偏刚度ka1、ka2/(N·rad-1)41 500质心距前轴距a/m1.185后轮侧偏刚度ka3、ka4/(N·rad-1)41 500质心距后轴距b/m1.075稳定杆侧倾刚度ksa /(N·rad-1)12 500前悬侧倾刚度kφf/(N·rad-1)25 700外倾角刚度 kγ/(N·rad-1)1 306后悬侧倾刚度kφr/(N·rad-1)17 000

3.1 实验车辆侧偏角及各轮中心速度计算

假设四轮初始前束和外倾角都设为零，后轮无转角，即δ3=δ4=0，以图3所示的侧偏角为正，在接近极限位置进行转向，选取几个速度时刻，如2、4、6、…、12 km/h(该速度可认为是汽车质心处的水平速度，由于稳态圆周运动对应唯一的速度，故纵滑和侧滑都是唯一的)，根据质心侧偏角β、横摆角速度r和式(28)～(31)可拟合出汽车不同速度下稳态转向四轮侧偏角曲线，结果如图5所示。

根据质心侧偏角β、横摆角速度r以及式(33)、(34)、(35)、(36)，得：

(33)

(34)

(35)

(36)

低速极限位置以不同车速进行稳态转向时，各轮行驶速度随车身质心S处车速的关系如图6所示。

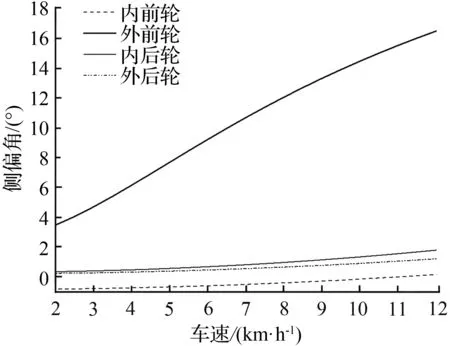
图5 不同速度下稳态转向时四轮侧偏角
Fig.5 Four tire slip angles at different of speedswith an error rate of 20% during steady state steering

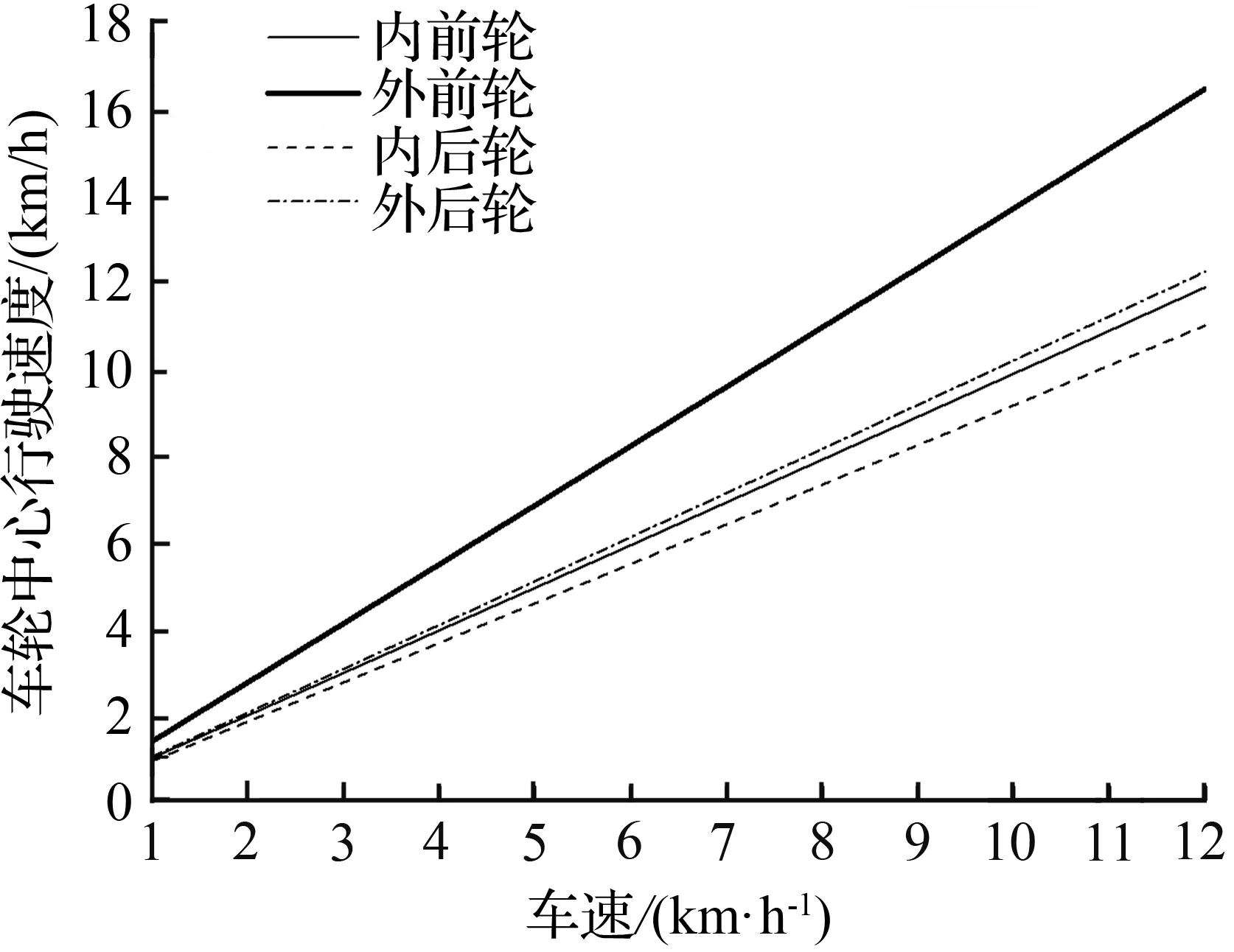
图6 各轮行驶速度与车速关系
Fig.6 Relationship between driving speedvaries with vehicle speed

由图5可知，车速为5 km/h，汽车在接近极限位置处稳态转向时，阿克曼转向误差率为55 %，各轮的侧偏角分别为内前轮-0.54°，外前轮7.6°，内后轮0.56°、外后轮0.38°，且在一定速度范围下，在不同车速下进行稳态转向时，随着速度的增加，内前轮侧偏角由负值变为正值，其他车轮始终为正值。由图6可知，车速为5 km/h且接近极限位置处进行稳态转向时，各轮中心行驶速度分别为内前轮4.9 km/h、外前轮6.8 km/h、内后轮4.54 km/h和外后轮5.05 km/h。

3.2 稳态纵滑侧偏联合工况

汽车匀速圆周运动时，即使车轮发生纵滑，车速也保持恒定，故滑移率也可以唯一确定。各轮胎上的纵向力、侧向力与车速、轮荷、侧偏角及滑移率有关，可由基于轮胎刷子模型的稳态纵滑侧偏联合工况模型法表示[9-10]。在该工况下将接触区分为附着区和滑动区，则附着区和滑动区的边界点可表示：

(37)

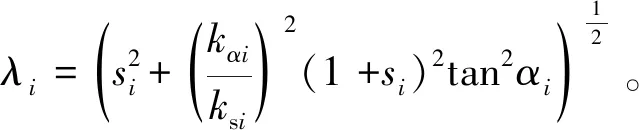
当存在驱动力时，ξi>0，有：

(38)

(39)

当ξi=0，有：

Fxi=-μFzicosεi，

(40)

Fyi=-μFzisinεi，

(41)

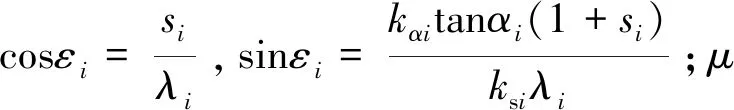
根据经验公式，滑动速度为：

(42)

最终得:

Fxi=Fxi(si,αi,uti,Fzi)，

(43)

Fyi=Fyi(si,αi,uti,Fzi)，

(44)

式中，si为各轮纵向滑移率；αi为轮侧偏角(°)；uti为各轮中心处行驶速度(m/s)；Fzi为各轮载荷(kN)。

在车速保持5 km/h，在接近极限位置处稳态转向且发生侧向载荷转移时，各轮纵向力和侧向力随纵向滑移率变化的情况，通过联立式(37)～(44)，可得到各轮纵滑侧偏关系如图7～10所示。

3.3 自回正力矩计算

轮胎的自回正力矩主要包括侧向力与纵向力引起的回正力矩[11]，同样可以用轮胎刷子模型的稳态纵滑侧偏联合工况模型法表示，则各轮在不同侧偏角下驱动力与自回正力矩关系如图11～14所示，可通过以下公式得到各轮自回正力矩，即：

(45)

式中，ti侧偏角为零时的轮胎拖距(m)；kyi为轮胎单位宽度的侧向刚度(N/m)。

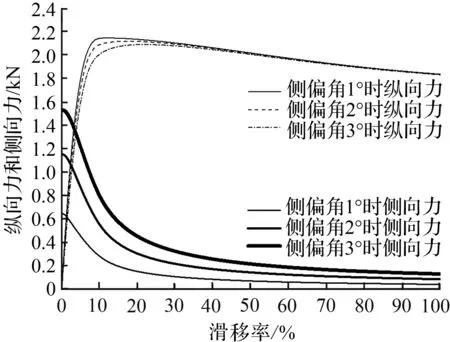
图7 内前轮纵向力和侧向力随纵向滑移率变化
Fig.7 Longitudinal and lateral forces of inner-frontwheel vary with longitudinal slip ratio

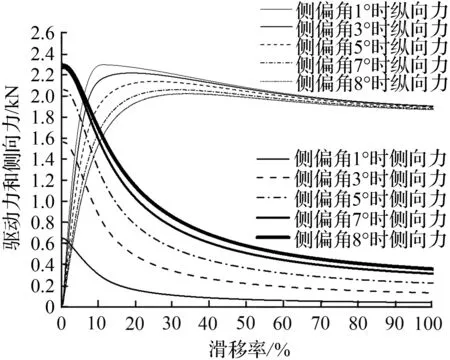
图8 外前轮纵向力和侧向力随纵向滑移率变化
Fig.8 Longitudinal and lateral forces ofouter-front wheel vary with longitudinal slip ratio

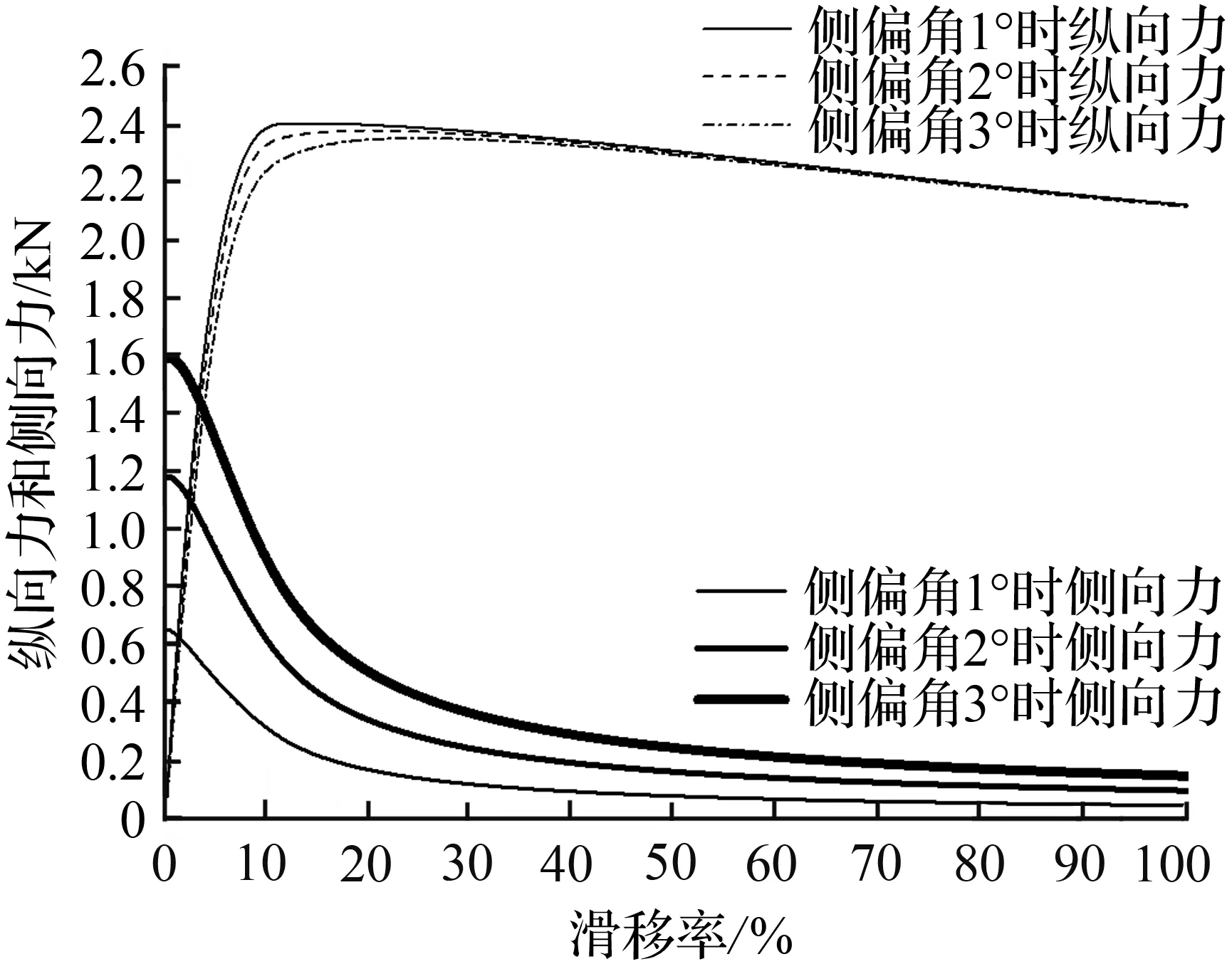
图9 内后轮纵向力和侧向力随纵向滑移率变化
Fig.9 Longitudinal and lateral forces of inner-rearwheelvary with longitudinal slip ratio

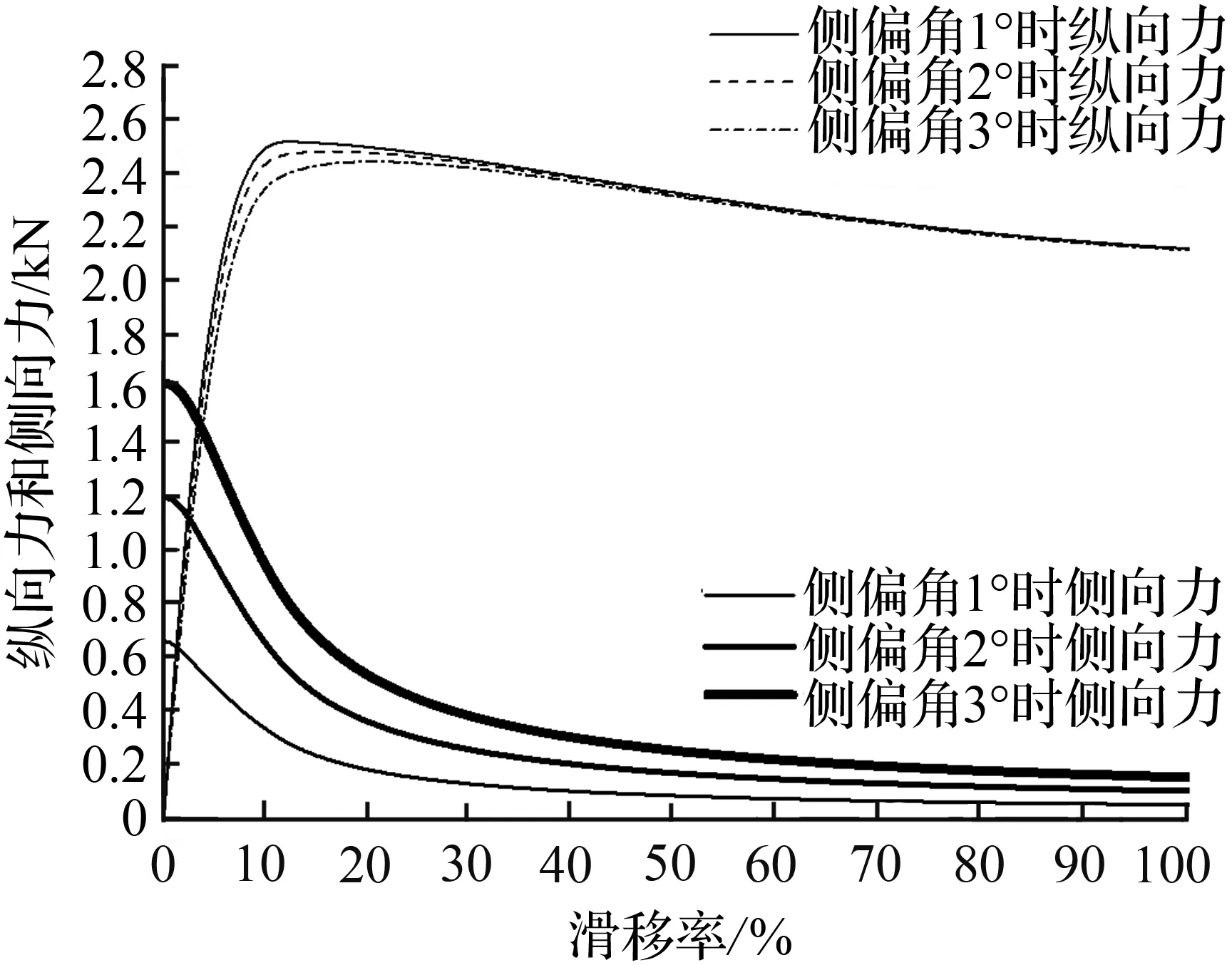
图10 外后轮纵向力和侧向力随纵向滑移率变化
Fig.10 Longitudinal and lateral forces of outer-rearwheel vary with longitudinal slip ratio

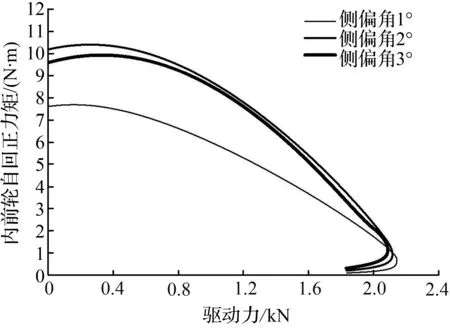
图11 内前轮自回正力矩随驱动力变化
Fig.11 Self aligning torque of inner-frontwheelvaries with driving force

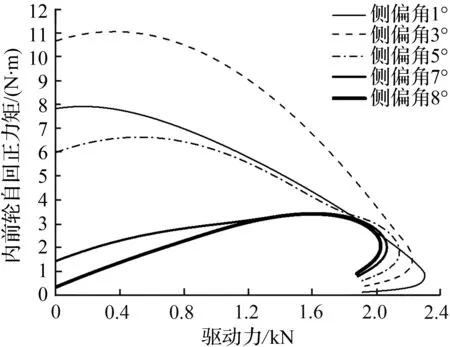
图12 外前轮自回正力矩随驱动力变化
Fig.12 Self aligning torque of outer-frontwheel varies with driving force

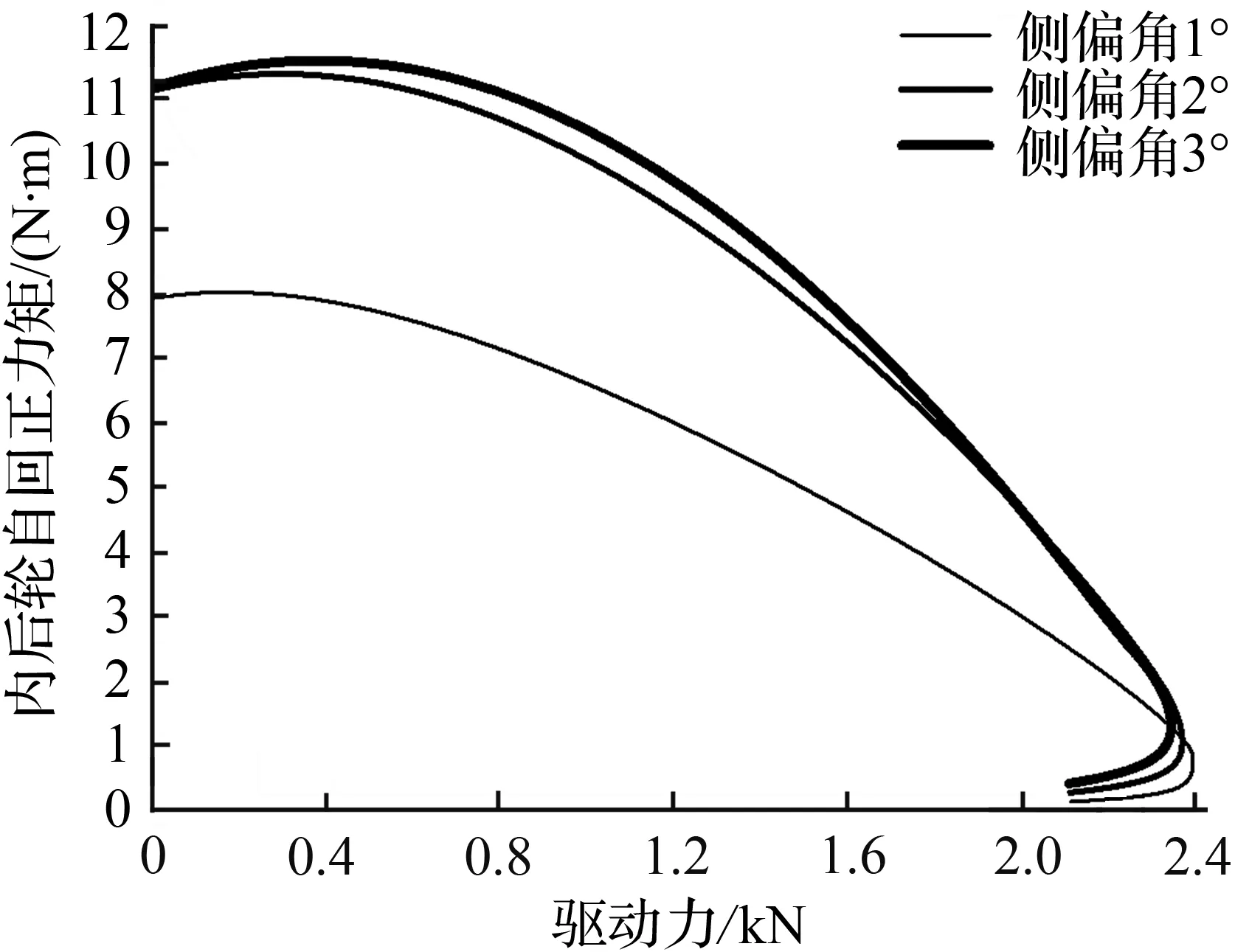
图13 内后轮自回正力矩随驱动力变化
Fig.13 Self aligning torque of inner-rear wheelvarieswith driving force

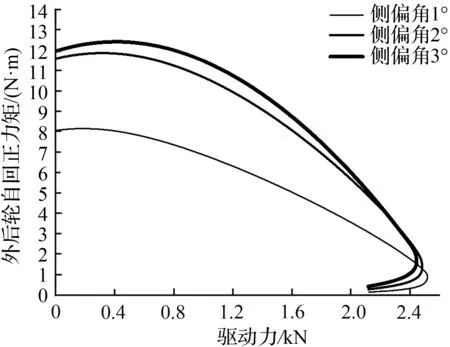
图14 外后轮自回正力矩随驱动力变化
Fig.14 Self aligning torque of outer-rearvaries with driving force

图11～14表示车速5 km/h且发生侧向载荷转移时侧向力和纵向力对自回正力矩的影响。由于外前轮受力最大，最先发生滑动，故可假设两后轮无纵向滑移，即Fx3=Fx4=0，则内后轮自回正力矩 5.4 N·m，外后轮自回正力矩为3.8 N·m。

3.4 前轮外倾侧向力回正力矩计算

由图形变换原理和文献[12]所述的计算方法，以转向中心内侧转向为正方向，计算获得外倾角、主销偏移距和主销后倾距随车轮转角的变化，结果如图15、图16所示。

由于后轮无外倾角变化，故只有前轮存在外倾角变化引起的侧向力回正力矩，可求得各轮外倾回力矩分别为内前轮约13 N·m、外前轮约为1 N·m。

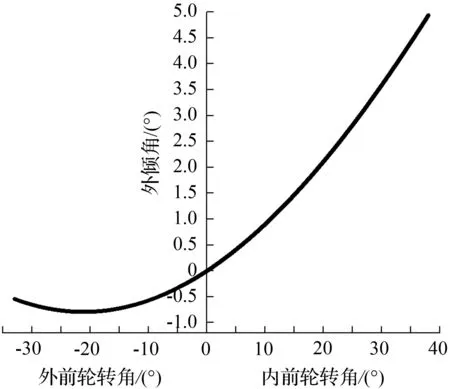
图15 前轮外倾角随转角车轮变化关系
Fig.15 Camber of front wheel varies withwheel angle of rotation

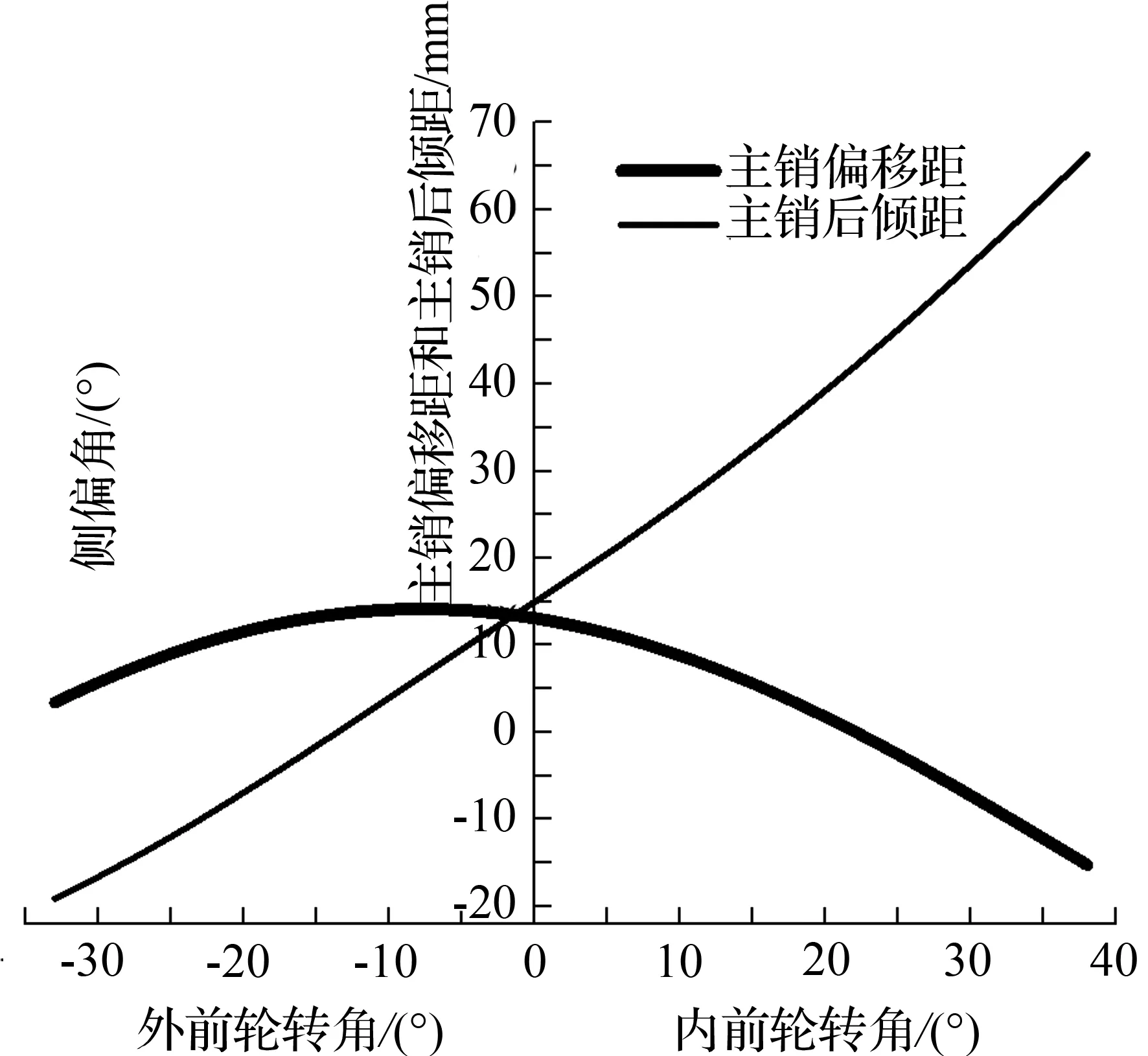
图16 前轮主销偏移距和主销后倾距随车轮转角关系
Fig.16 Kingpin offset at ground and castor trailvary with wheel rotation angle

3.5 侧向力与驱动力计算

由实验车辆驱动特性可认为转向时驱动力大致相等，即Fx1=Fx2，可以利用反证法计算得知。若四轮纵向滑移率为零时，根据式(9)～(12)，各轮侧向力分别为内前轮为-0.393 kN，外前轮2.295 kN，内后轮为0.408 kN，外后轮为0.278 kN，然而，在地面附着系数0.8路面上，地面很难提供外前轮侧向力需求，故汽车外前轮必定存在滑移现象，前轮所需侧向力需重新校正计算，即采用纵滑侧偏工况计算。

由刷子模型的稳态纵滑侧偏联合工况模型，并根据式(9)～(12)可求得各轮驱动力和侧向力，得到内前轮和外前轮驱动力均为0.796 kN，内前轮侧向力为 -0.2 kN，外前轮侧向力为2.045 kN，内后轮、外后轮侧向力不变，分别为0.408 kN和0.278 kN。

由图8、图9对比可知，在车速5 km/h以及方向盘接近极限位置转向时，内前轮与外前轮均存在纵向滑移，但滑移率均小于5 %。与无纵滑分析的侧向力相比，内前轮、外前轮侧向力绝对值均得到一定程度的减小。

4 阿克曼转向误差验证

阿克曼转向误差也是轮胎低速侧滑的主要原因，而轮胎的侧滑主要与侧向力和回正力矩有关，为了进一步分析阿克曼转向误差对低速侧偏特性和回正性能的影响，设定阿克曼转向误差率εO在20 %和80 %两种情况下进行讨论，在接近极限位置进行转向，选取几个速度，如2、4、6、…、12 km/h，根据质心侧偏角β、横摆角速度r和式(28)～(31)可拟合出汽车不同速度下稳态转向四轮侧偏角曲线，结果如17～18所示。

对比图17、图18与图5可见，相比原车阿克曼转向误差率55 %的情况，阿克曼转向误差率为80 %、汽车方向盘接近极限位置且在5 km/h稳态转向时，汽车方向盘向极限位置运动倾向更为明显，而当误差率为20 %时，该影响大大减小。

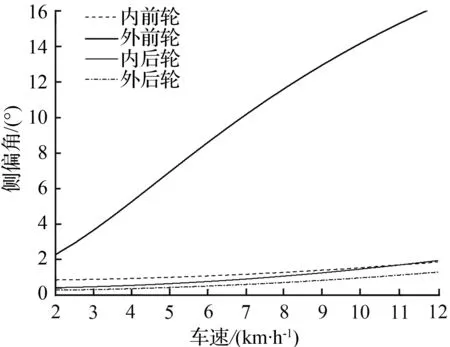
图17 误差率为20%时不同速度下稳态转向四轮侧偏角
Fig.17 Four tire slip angles at different of speeds withan error rate of 20% during Steady state steering

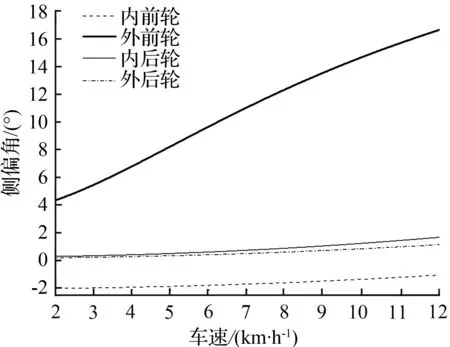
图18 误差率为80%时不同速度下稳态转向四轮侧偏角
Fig.18 Four tire slip angle at different of speeds withan error rate of 80% during Steady state steering

5 结论

①在纵滑侧偏工况下，内前轮和外前轮驱动力均为0.796 kN，内前轮侧向力为 -0.2 kN，外前轮侧向力为2.045 kN，内后轮、外后轮侧向力不变，分别为0.408 kN和0.278 kN。与无纵滑时的侧向力相比，内前轮、外前轮侧向力绝对值均得到一定程度的减小，更接近实际观测值。

②汽车方向盘接近极限位置且在5 km/h稳态转向时，汽车方向盘向极限位置运动倾向更为明显，当误差率为20 %时，该影响大大减小。因此，在保证较高速转向侧向力需求的同时尽量减小阿克曼转向误差，可以避免极低速转向时方向盘向极限位置运动倾向，防止低速大转角转向时方向盘难以控制的现象。

③考虑了载荷转移和定位参数等影响因素和基于轮胎刷子模型的纵滑侧偏工况，能够较好地解决低速大转角问题，可为高速大转角转向研究提供参考。