地下水封洞库洞室轴线方向优化方法
1313
(1.福州大学 环境与资源学院,福州 350116;2.国土资源部丘陵山地地质灾害防治重点实验室(福建省地质灾害重点实验室), 福州 350116;3.福州大学 地质工程福建省高校工程研究中心,福州 350116)
1 研究背景
地下水封洞库是利用地下水密封技术储存石油、液化石油气(LPG)等能源的新型工程型式,其实质是包含交通巷道、通风巷道、水幕巷道、操作竖井、通风竖井、洞室及连接巷道等多种地下结构类型的大型地下洞室群。其中,洞室是用于储存油气的关键地下结构,科学合理地优化其轴线方向(轴向)对于施工安全、减少支护量及长期稳定性等具有重要的理论意义和工程价值。
目前,针对地下水封洞库洞室轴向确定原则及优化方法、指标等问题研究较少,仅有宋琨等[1]以关键点位移和塑性区面积作为评价指标确定出最优轴向。其他相关研究主要集中在传统线性地下工程方面。在轴向确定原则研究上:戚蓝和马启超[2]认为地下厂房长轴线方向与最大主应力方向尽可能形成较小夹角,与主要断裂带的走向尽可能形成较大夹角;周建民等[3]根据各节理组的权重,以节理平均方位角与洞室轴向大角度相交确定出洞室轴向;倪绍虎等[4]得出岩层走向与洞室轴线的夹角不宜<70°;王俊奇和颜月霞[5]计算发现洞轴与最大水平地应力平行布置时可增大顶底板稳定性,洞轴与最大水平地应力方向大角度相交时可增大边墙稳定性;张玉升[6]得出洞轴一般应与最大水平主应力小角度相交,与优势结构面走向大角度相交。轴向优化方法及评价指标研究方面:李莉等[7]采用英格里公式法,以洞室切向应力为评价指标,进行水电厂房轴向优化;Zhang等[8]基于开挖荷载释放系数开展了水电厂房轴向优化研究;王震洲等[9]基于三维非线性有限元,以围岩变形和塑性区为指标,优化了水电厂房轴向。对于块体稳定性为主控问题的地下工程,相关学者[10-13]基于关键块体理论,以关键块体大小、数量和稳定性为指标,优化洞室轴向。另外,较大的轴向应力可能导致的围岩分区破裂现象[14]、与轴向垂直的中间主应力效应[15]、地下水对轴向的影响[16]等问题也得到了重点研究。
综上可知,目前从围岩稳定性角度开展的轴向研究一般仅针对特定的地下工程类型,由于未全面考虑地下水封洞库工程特性而难以将其推广应用至水封洞库洞室轴向优化中。由于地下水压力密封技术要求高,目前地下水封洞库主要处于花岗岩类地层,岩体中含有大量随机结构面,洞室埋深主要为100~400 m。工程实践表明,洞库洞室围岩变形破坏同时存在着受地应力控制的岩体强度型破坏、受结构面控制的块体掉落/滑落型破坏和受地应力-结构面协同控制的围岩破坏(为主要破坏模式)等。基于此,本文针对地下水封洞库工程特性,基于等效连续介质模型、非连续介质模型和关键块体理论,依托3DEC和Unwedge数值分析平台,提出了一种洞室轴向优化方法,并将其应用于山东某地下水封洞库洞室轴向确定中,以期得出有益于洞库洞室轴向设计及工程实践的研究结论。
2 洞室轴向优化方法及评价指标
地下水封洞库洞室轴向优化的本质是优化围岩稳定性,在洞室轴向优化研究中需要考虑的首要因素是围岩变形破坏模式及机理。洞库工程实践及相关现场监测数据表明,围岩变形破坏模式存在应力-强度控制型、结构面控制型和应力-结构面协同控制型等形式,在洞室轴向优化方法选择上,应采用能揭示上述3种围岩变形破坏模式的方法,选取的评价指标应能反映特定变形破坏模式下围岩稳定性或支护安全性。基于上述考虑,本文提出了适用于地下水封洞库工程特性的洞室轴向综合优化方法及其评价指标体系(图1)。其关键步骤叙述如下。

图1 地下水封洞库洞室轴向优化关键步骤Fig.1 Key steps of optimizing the axis direction ofunderground water-sealed storage cavern
(1) 基于相关规范确定洞室轴向可选范围。根据洞库相关规范[17-18],当建库场地以垂直地应力为主或处于低地应力区时,轴向应与岩体主要结构面呈大角度相交,同时应适当兼顾与次要结构面的交角;当以水平地应力为主或处于高地应力区时,轴向应与近水平最大主应力方向平行或小角度相交。这种确定原则与目前的相关研究结论基本类同,其困难之处在于高、低地应力区难以判别。基于文献[19],以岩石饱和单轴抗压强度Rc与垂直洞室轴向的最大初始应力σmax的比值来评判地应力高低,Rc/σmax<4为极高地应力区,4≤Rc/σmax<7为高地应力区,无中、低地应力区指标。而由目前国内已建和在建的10余处地下水封洞库工程可知,Rc/σmax一般在7左右(7~8.5居多),围岩高应力破坏现象不明显;但是,场地一般又以水平地应力为主。
因此认为,初步确定出的洞室轴向可选范围宜兼顾优势结构面走向和地应力方位两者,总体上应与尽可能多的优势结构面组的走向大角度相交、与水平最大主应力小角度相交。
(2) 应用等效连续介质模型分析方法获取应力-强度控制型围岩破坏模式下的洞室最优轴向。在等效连续介质模型中可把岩体随机结构面以及复杂地下水环境都以等效岩体力学参数来表征,应用有限元法、有限差分法等连续介质数值分析方法可实现该类模型的力学计算。为了全面反映该类模型条件下围岩稳定性,选取围岩最大位移、塑性区体积和稳定系数作为围岩稳定性状况评价指标。本步骤的总体流程为:将步骤(1)确定的洞室轴向可选范围每隔1°或2°分成若干工况;对各轴向工况进行力学计算;分析各评价指标随轴向的演变规律,获取等效连续介质模型条件下的最优洞室轴向。值得指出的是,以往的轴向研究几乎都忽视了开挖过程中掌子面的稳定性问题,但掌子面的稳定性在开挖施工过程中相当重要且突出,因此认为,构建的等效连续介质数值模型应包含掌子面及四周围岩,如此才能全面反映施工过程安全性。
本文中,围岩稳定系数通过强度折减法获得(由于围岩破坏机制有剪破坏和拉破坏2种,郑颖人等[20]研究表明需要同时对抗剪、抗拉强度进行同等程度的折减),公式为
(1)

应用强度折减法求解稳定系数时,目前主要以计算不收敛、位移-折减系数曲线的位移突变点等作为临界折减系数(稳定系数)评判指标。通过反复试算发现,基于计算不收敛获取的临界折减系数往往较大,而应用位移-折减系数曲线的位移突变点作为评判指标较为合理,建议采用此评判方法。特别指出,当位移突变并超出了文献[21]建议的围岩允许相对收敛值(表1)时,其获取的临界折减系数(稳定系数)应更为可靠。

表1 洞周位移允许相对收敛值Table 1 Allowable relative convergence of displacementaround the cavern
(3) 应用非连续介质模型分析方法获取应力-结构面协同控制型围岩破坏模式下最优洞室轴向。限于目前的勘测和计算水平,构建真实的岩体结构模型是不可能的,而通过在等效连续介质模型中加入部分优势结构面的方式可基本反映应力-结构面协同控制型围岩破坏模式。该步骤的分析流程与步骤(2)大体相同,但根据非连续介质模型条件下洞室围岩的破坏特征,进一步考虑以结构面最大剪位移作为评价指标,同时,该模型下围岩最大位移指的是岩块的最大位移。目前,离散介质条件下地下工程围岩强度折减法研究极少,参考文献[20]和文献[22]的研究结论,认为应对岩块、结构面的抗剪强度参数、抗拉强度参数同时进行同等程度的折减,这也是该模型计算稳定系数时与等效连续介质模型不同之处。
(4) 应用关键块体理论获取结构面控制型围岩破坏模式下最优洞室轴向。关键块体理论能获得任意3组结构面与临空面组合情况下最不利关键块体的稳定性及几何状况,可用于研究块体稳定性等结构面控制型围岩破坏模式下最优洞室轴向,基于Unwedge等计算软件可实现此类计算。选取关键块体的稳定安全系数为1.5时所需的支护压力作为洞室轴向的评价指标,该指标能全面反映洞室不同部位可能形成的块体大小、数量、厚度及稳定系数等信息。通过分析支护力随洞室轴向的演变规律,可确定出最优洞室轴向。
(5)综合各种分析方法的评价指标结果确定出最优洞室轴向。由于洞室轴向优化研究主要在洞库开挖之前进行,此时对洞室区工程地质条件尚掌握有限,因此需将各种计算结果相互对比并综合确定出最优洞室轴向。从不同角度获得的评价结果主要有2种情况:①各种计算结果基本相近,可取其平均值为最优洞室轴向;②各种计算结果相差悬殊,可根据具体工程特征确定围岩主要破坏模式,并主要依据反映该种破坏模式的计算结果确定最优洞室轴向。
3 洞库实例应用
3.1 实例概况
以山东某地下水封洞库工程作为应用研究实例。该场地的地表高程为40~150 m,设计洞室顶点高程为-120 m,建库岩体为花岗岩,选址时已避开了断层和主要破碎带,对围岩稳定性有重要影响的主要是岩体节理。依据产状进行节理分组,由洞库场地勘察资料可知,洞室区主要发育4组优势节理,其编号和优势产状分别为:J1(100°∠65°),J2(87°∠35°),J3(302°∠36°),J4(283°∠71°)。对洞室场地实测地应力进行张量分析求取平均值,经张量计算确定出水平最大主应力方向为N78°E,并通过线性回归分析,获得了反映地应力场的公式为
(2)
式中:σH为最大主应力(MPa,水平方向);σh为中间主应力(MPa);σv为最小主应力(MPa,竖直方向);h为高程(m)。
进行等效连续介质模型和非连续介质模型分析时,合理、准确的岩体物理力学参数是关键。由于洞室轴向优化研究处于初步设计/详细设计阶段,此时尚未进行洞室开挖、监测,无法进行洞室岩体的现场力学试验和参数反演。因此,本文利用经验估算和工程类比法综合确定岩体物理力学参数。基于钻孔岩芯和钻孔摄像等资料,应用Q分类法[23]进行洞室围岩质量分级,具体公式为
(3)
式中:RQD为岩石质量指标;Jn为节理的组数系数;Jr为节理的粗糙度系数;Ja为节理风化蚀变系数,Jw为地下水的影响系数;SRF为应力折减系数。为利用Hoek-Brown准则估算岩体力学参数,需建立Q值与GSI(地质强度指标)之间的联系。Hoek[24]提出,假定Jw和SRF都为1时,GSI和Q值之间的关系式为
(4)
大量洞库工程实例及场地的钻孔压水试验表明,洞室围岩出水处的水量一般<5 L/min,按Q分类法,Jw为1;该洞室不处于高、极高地应力区,按Q分类法,SRF为1。因此,可通过式(4)建立Q值与GSI的联系。需要强调的是,该公式实质上已经考虑了复杂的地下水动态环境,即把地下水渗流的影响等效地考虑到岩体力学参数之中,故后续的相关计算不需要重复考虑地下水渗流。详勘报告揭示,该场地Q值为[4,10)的岩体占67%,从安全角度考虑,选取该质量等级的Q值下限4进行计算分析。因此,Q′也为4,GSI为56。
Hoek-Brown强度准则[25]公式为
(5)

(6)
式中:GSI为地质强度指标,本次取56;mi为岩石材料常数,本次取30;D为岩体因受爆破、应力释放而造成的岩体质量劣化、参数降低的量化因素,本次取0。
通过式(7),可将Hoek-Brown强度曲线的非线性转换为线性,得出等效内聚力c′、内摩擦角φ′。
(7)
其中,
(8)
对于地下工程,有
(9)
式中:r为洞室埋深部位岩体的重度(MN/m3);H为洞室的埋深(m),当水平应力大于垂直应力时,rH被最大水平应力取代。由于该场地垂直应力为最小主应力,故rH取洞室区最大水平应力,本次取10 MPa。
综上所述,可获得Q值为4时洞库岩体等效力学参数。为了更全面地确定等效岩体力学参数,对洞库场地的50余处钻孔岩体同时进行了Q分类和BQ分类,发现4≤Q<10的岩体相当于BQ分类中的Ⅲ级岩体。故应用规范[19]建议的参数对Hoek-Brown准则确定的岩体力学参数进行适当微调(使参数处于该规范建议的取值范围内),最终确定的等效岩体力学参数如表2所示,其中岩体重度为26 kN/m3。

表2 岩体等效力学参数Table 2 Equivalent mechanical parameters of rock mass
在结构面力学参数取值中,抗剪、抗拉的力学参数来自于勘察报告,同时按结构面的连通率为0.9进行等效转换。结构面的法向刚度取决于岩体的弹性模量,考虑结构面泊松效应,法向刚度约取切向刚度的2倍。最终确定出的结构面力学参数见表3。

表3 结构面力学参数Table 3 Mechanical parameters of discontinuity
3.2 洞室轴向可选范围
基于该洞库工程地质条件,按照洞室轴向的确定原则:宜兼顾优势结构面走向和地应力方位两者,总体上应与尽可能多的优势结构面组的走向大角度相交、与水平最大主应力小角度相交,由此确定出洞室轴向的可选范围为NE50°~90°。

图2 等效连续介质条件下洞室区数值模型Fig.2 Numerical model ofcavern in the presence ofequivalent continuousmedium
3.3 等效连续介质模型分析
基于3DEC数值分析平台(不考虑结构面时为有限差分法),构建的洞室区等效连续介质数值模型见图2,其中洞室截面为马蹄形(跨度22 m、高度26 m),模型轴向长度为55 m,岩体等效力学参数按前述内容施加。基于洞室轴向可选范围NE(50°~90°),每间隔1°计算1次(施加与之相应的地应力场)。由于掌子面稳定性是影响洞室施工安全的重要因素,因此在数值计算中需考虑掌子面的影响,在此次计算中主要表现为数值模型最后10 m不开挖。图3为洞室轴向为NE78°时掌子面及围岩位移分布,对比可知,边墙和掌子面处位移较大,拱顶和底板较小,其他轴向工况下的位移分布特征与之类似。
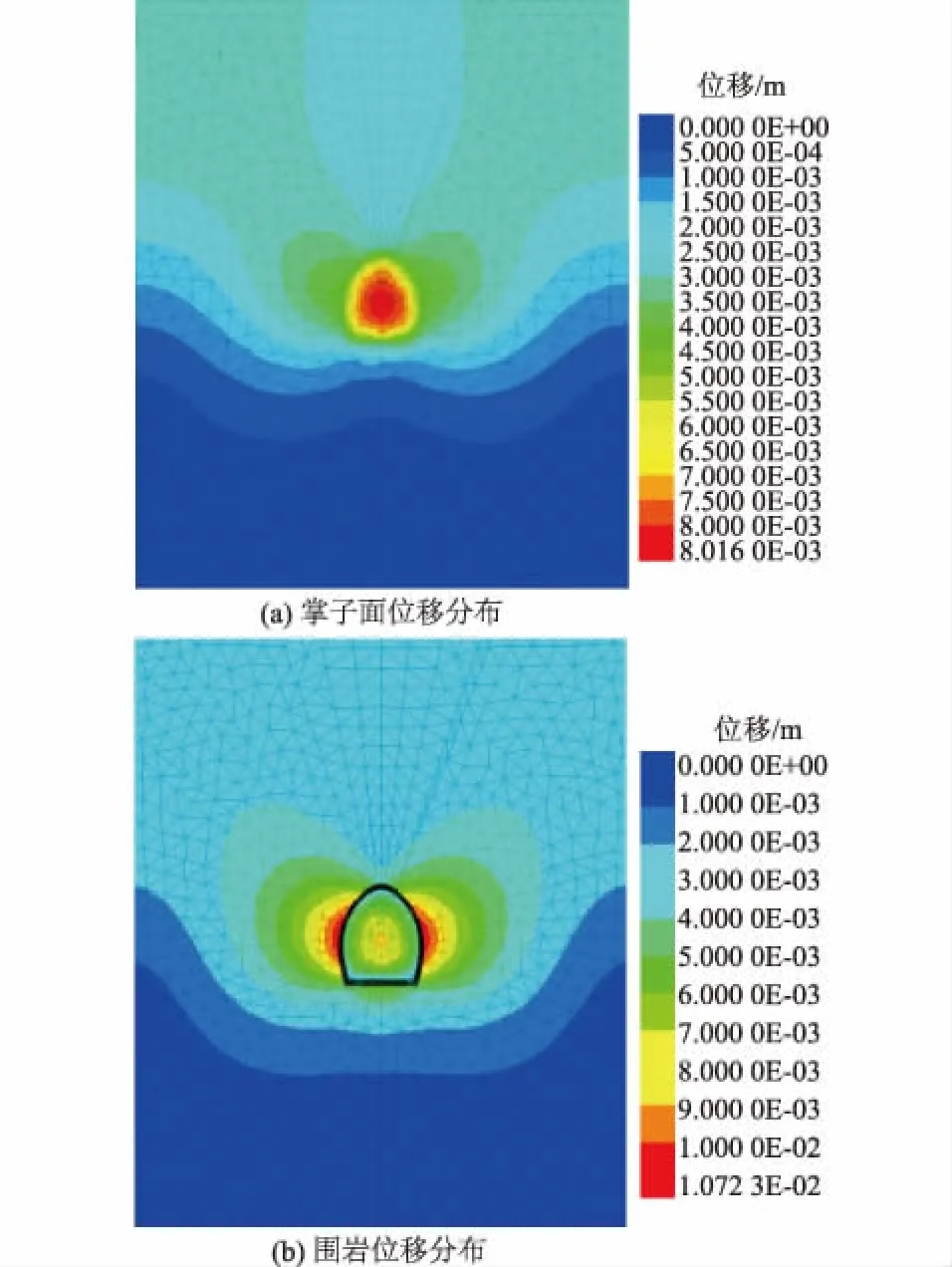
图3 轴向NE78°工况下掌子面及围岩位移分布Fig.3 Displacement distribution of working face andsurrounding rock when axis direction is NE78°
各评价指标计算结果见图4。由图4可知,最大位移和塑性区体积都随轴向变化呈现先减小后增大的规律,稳定系数呈现先增大后减小的规律,计算结果较统一,3个指标指向的最优轴向为NE(77°~79°)。该结果与最大主应力方向基本接近,表明等效连续介质模型主要反映地应力对轴向的影响。

图4 围岩最大位移、塑性区体积及稳定系数随轴向演化规律Fig. 4 Variations of maximum displacement, volume ofplastic zone, and stability coefficient of surroundingrock with the change of axis direction
3.4 非连续介质模型分析
在上述等效连续介质模型的基础上,施加场地发育的4组优势结构面(间距20 m,由于前述结构面力学参数已经考虑了连通率,因此该模型施加贯通性结构面),构建出洞室区非连续介质模型(图5),其中轴向每隔1°变化时,结构面优势产状在模型中也要相应变化。此种模型条件下,由于考虑结构面随机切割产生的力学效应,掌子面稳定性问题更加突出。图6为非连续介质模型下洞室轴向NE78°时的掌子面位移和塑性区分布,可以看出,掌子面位移较大且在应力调整过程中出现了一定程度的塑性区。

图5 非连续介质条件下洞室区数值模型Fig.5 Numerical model of cavern in the presence ofdiscontinuous medium
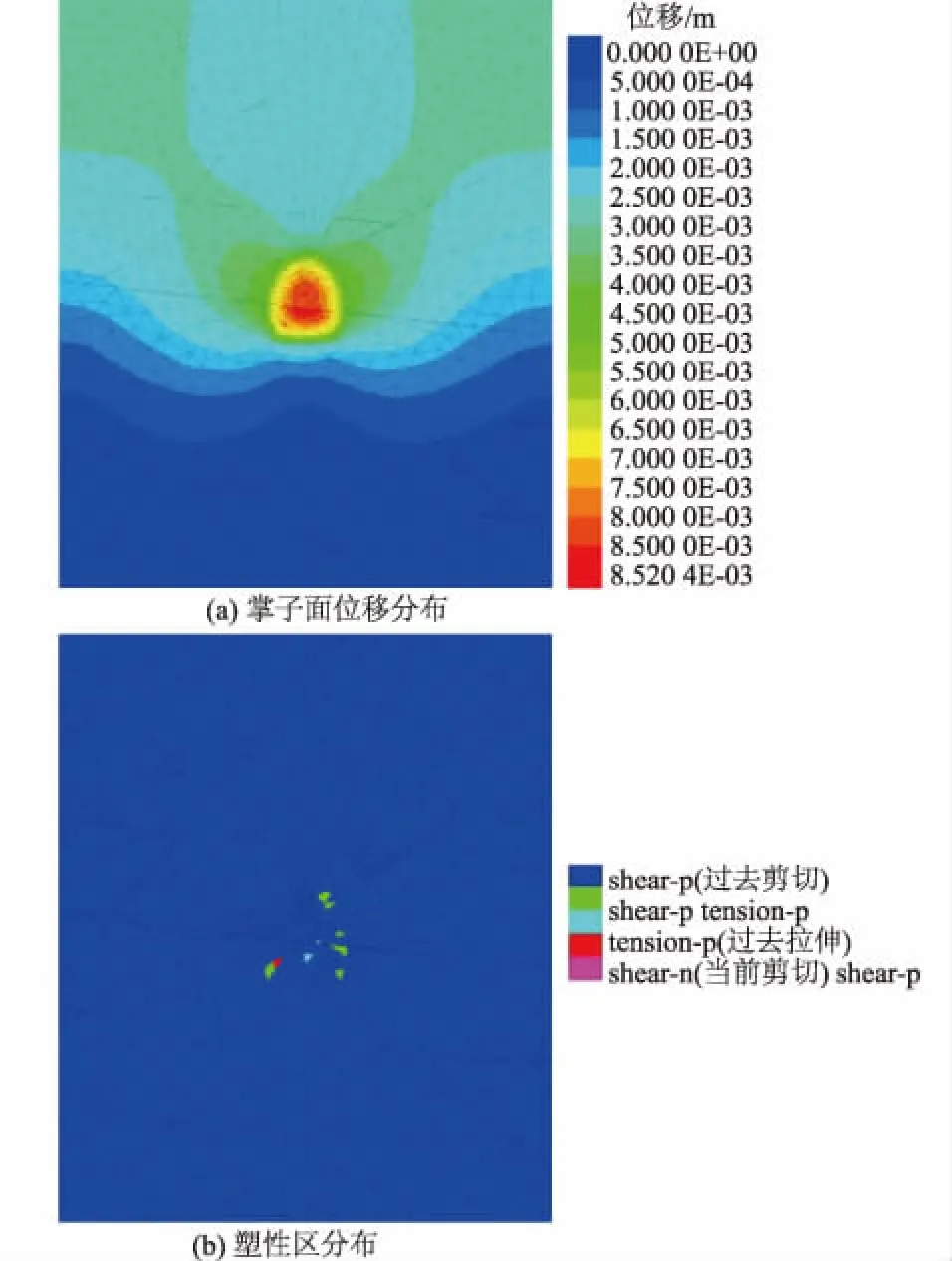
图6 非连续介质模型下洞室掌子面位移及塑性区分布Fig.6 Displacement and plastic zone distribution ofworking face in the presence of discontinuous medium

图7 围岩最大位移、塑性区体积、稳定系数及结构面最大剪位移随轴向演化规律Fig.7 Variations of maximum displacement, volume ofplastic zone, stability coefficient of surrounding rock,and maximum shear displacement on joint surface withthe change of axis direction
各评价指标计算结果见图7,由图7可知,各指标演化规律与等效连续介质模型分析计算结果类同。4个指标指向的最优洞室轴向为NE78°~82°,该值与等效连续介质分析结果较为接近,只有3°左右的偏差。分析认为,出现该现象的原因在于该场地的优势结构面走向已经与水平最大主应力大角度相交,因此2种模型的计算结果指向的最优洞室轴向相似。
3.5 关键块体理论分析
在不同洞室轴向下结构面自由组合形成的关键块体所需支护力大小是本次研究中重点关注对象。在关键块体理论分析中无需考虑结构面连通率等因素影响,为了能够更加准确地判别洞室轴向优劣,在进行分析时,考虑洞室围岩稳定较为不利的情况(危险工况,设置较低的结构面力学参数),开展最优轴向分析。基于上述考虑,将各组优势结构面的内摩擦角φj、内聚力cj和抗拉强度σtj设置为:φj=35°,cj=0,σtj=0。优势结构面编号及其产状按前述施加,4组优势结构面有4种组合形式。洞室某轴向(倾伏向/倾伏角)和结构面产状(倾角/倾向)的赤平投影如图8所示;图9为主洞室轴向为NE80°时,结构面J1/J2/J4组合下形成的块体示意图,关键块体达到稳定性要求所需支护力大小为0.07 kN/m2。

图8 洞室轴向和结构面产状的赤平投影Fig.8 Stereographic projection of cavern’s axisdirection and dominant joint surface

图9 轴向NE80°时J1/J2/J4结构面组合下的块体示意图Fig.9 Diagram of block in the presence of J1/J2/J4discontinuities combination when axis direction is NE80°
计算结果表明,J1/J2/J3结构面组合下没有形成不稳定块体,无需支护,其他3种组合形式所需的支护压力(块体稳定安全系数为1.5)见图10。由图10可知,当洞室轴向为NE55°~60°和NE80°~90°时,各种结构面组合下的总体支护力均相对较小,为较优洞室轴向。

图10 不同结构面组合下支护压力随轴向演化规律Fig.10 Variations of support pressure with the changeof axis direction in the presence of differentcombinations of discontinuities
需要指出的是,基于关键块体理论获得的最优结果与前述2种方法并不完全一致,表明不同围岩破坏模式对应的最优轴向不同。由于关键块体理论只能研究四面体稳定性问题,且无法考虑结构面间距等因素,因此需将上述3种计算结果综合对比,以全面确定出最优洞室轴向。
3.6 综合判定
综合上述等效连续介质模型、非连续介质模型和关键块体理论分析结果可知,各评价指标确定的最优洞室轴向范围有较接近的方位区域,大体为NE78°~85°范围,按照总体取平均值的方式,可确定NE82°为最优洞室轴向。
需要指出的是,由于本文提出的洞室轴向综合优化方法是从围岩稳定性角度出发的,未考虑油气进出便利性、操作竖井位置、征地范围以及与原有水封洞库(装置)的距离等因素,因此最终洞室轴向可基于这些因素进行适当调整。
4 结 论
本文基于地下水封洞库工程特性,提出适宜于该工程特性的洞室轴向优化方法,经洞库实例应用,得到了以下结论:
(1)提出的洞室轴向优化方法具有以下关键步骤:①基于洞库相关规范确定出洞室轴向可选范围;②基于等效连续介质模型,以围岩最大位移、塑性区体积和稳定系数为评价指标,获取最优洞室轴向;③基于非连续介质模型,以岩块最大位移、塑性区体积、稳定系数及结构面最大剪位移为评价指标,确定出该模型条件下的最优洞室轴向;④基于关键块体理论,以支护压力为评价指标,确定出该条件下的最优轴向;⑤综合各评价指标结果,全面评判确定最优洞室轴向。
(2)在构建数值模型时,应构建含掌子面的洞室区数值模型,以全面反映围岩稳定性的轴向效应。在应用等效连续介质模型、非连续介质模型和关键块体理论优化洞室轴向时,通过将轴向可选范围每隔1°或2°分成若干工况,分析各评价指标随轴向的演变规律,可合理地获取各种围岩破坏模式下的最优洞室轴向。基于强度折减法确定围岩稳定系数时,使用位移-折减系数曲线的位移突变点作为临界折减系数评判方法较计算不收敛评判法更为合理。
(3) 将提出的地下水封洞库洞室轴向综合优化方法应用于洞库工程实例,证实了该方法的可行性,优化结果能基本表明该方法的可靠性。需要指出的是,本文提出的洞室轴向综合优化方法是从围岩稳定性角度出发的,未考虑油气进出便利性、操作竖井位置、征地范围以及与原有水封洞库(装置)的距离等因素,因此最终洞室轴向可基于这些因素进行适当调整。

