基于能量法的超长桩屈曲稳定影响因素分析

3.45

(1.中国地质大学(武汉) 工程学院，武汉 430074；2.中国地质大学(武汉) 岩土钻掘与防护教育部工程研究中心， 武汉 430074；3.广西大学 土木建筑工程学院, 南宁 530004；4.广西大学 广西防灾减灾与工程安全重点实验室, 南宁 530004； 5. 广西大学 工程防灾与结构安全教育部重点实验室， 南宁 530004)

1 研究背景

随着建筑行业的快速发展，超长桩被广泛运用到超高层建筑与大型桥梁建筑中。对于大多数桩来说，在实际工程中往往同时受到水平荷载与竖向荷载组合的作用，其承载机理极为复杂[1]。对于长桩的承载性能，学者们从各个角度进行了研究：张骞等[2]研究了软土地区超长单桩的承载特性，得到桩顶沉降大部分来自于桩身压缩；胡念等[3]研究了超长嵌岩钻孔灌注群桩承载特征与受力机理，发现群桩沉降在加载和卸载阶段均与荷载成近似线性增加关系；王孝兵等[4]对大直径长桩在倾斜荷载下的基桩承载性能做了研究，得到了荷载倾角不同时，基桩承载特性也不同的结论。虽然学者们研究了普通长桩的承载力，但与普通桩不同，超长桩除了受竖向承载、水平承载外还因为长细比较大容易产生屈曲破坏，尤其是软土地基中的超长桩则更容易出现屈曲失稳问题。针对桩的屈曲稳定性问题，国内外学者做了大量研究，如：Davisson 和Robinson[5]基于m法得到部分埋置桩屈曲临界荷载的计算公式；Reddy 和 Valsangkar[6]采用m法和能量原理得到了完全埋置桩和部分埋置桩临界承载能力的分析模型；胡人礼[7]首先基于m法提出一组桩身有效计算长度L的经验公式。随后，沪煤工[8-9]引入能量原理，用里兹法和Timoshenko法讨论了m法设计桩基的有效计算长度；赵明华等[10]采用最小势能原理讨论了桩侧摩阻力对基桩屈曲稳定性的影响，发现桩侧摩阻力对基桩屈曲稳定的影响很小，一般可忽略不计。进一步，学者们提出了与实际较符合的m法与常数结合的组合土抗力形式。基于此方法，王成等[11]、姚文娟等[12-13]、周淑芬等[14]先后运用里兹法对超长桩进行了屈曲稳定性分析，发现组合抗力模式对于超长桩的稳定分析更为贴近。之后，刘礼标等[15]基于里兹法，用2段都为m法的双线性组合土抗力形式对超长桩进行了屈曲稳定性分析。后来，李传勋等[16]考虑了桩身自重，得出埋置率较低时桩自重对桩的屈曲临界荷载影响较大的结论。再后来，李威等[17]、唐文栋等[18]基于土抗力不随入土深度线性增长的C法，运用里兹法对超长桩进行屈曲稳定性分析，讨论桩身自重、桩侧摩擦对屈曲临界荷载的影响。

总之从已有的软土地基中超长桩的屈曲稳定性研究可知：①对于土抗力形式，大部分学者采用的m法与常数组合的土抗力形式，而采用土抗力不随入土深度线性增长的C法与常数组合的组合土抗力形式研究计算较少；②对于计算因素考虑，大部分学者计算时只考虑了单一因素，如只考虑自重或只考虑摩擦力，而同时考虑桩身自重与桩侧摩擦力大小的研究较少；③对于影响因素分析，大部分学者仅仅考虑了桩的埋置率、桩身自重、桩周摩擦力等因素，而同时考虑完整的桩的挠曲函数、土抗力形式、桩周土性质、桩自身性质等因素对桩的屈曲临界荷载影响分析却鲜有报道。

鉴于此，本文同时考虑桩身自重和桩侧摩阻力，采用C法与常数法组合的土抗力模式，基于能量法建立超长桩的屈曲临界荷载公式；基于所得公式，详细分析了桩的挠曲函数、土抗力形式、桩周土体性质、桩自身性质等因素对桩屈曲临界荷载的影响，为工程中超长桩的设计和运用提供理论参考依据。

图1 超长桩屈曲荷载计算模型Fig.1 Model of buckling analysis of extra-long pile

2 研究模型与基本假设

图1为超长桩屈曲稳定性分析计算模型，其中，坐标原点设定在桩底，桩顶竖向荷载为P，L为桩完整长度，h为基桩入土深度。基桩分为2段：上部为自由桩段，长度为L-h；下部为嵌固桩段，长度为h。土抗力常数计算部分长度为H。

模型的基本假设条件为：

(1)桩底固定，桩顶自由。

(2)桩侧土体的弹性抗力q采用C法与常数法结合的组合土抗力模式计算，即OA段采用常数法的土抗力计算模式，AB段采用C法的土抗力计算模式。基于此，可得桩侧土土抗力公式为

(1)

式中:m为桩侧土水平抗力的比例系数;b为桩身的计算宽度。根据规范可以知道，对于圆形桩，当桩径d<1 m时，b=0.9(1.5d+0.5)；当d≥1 m时，b=0.9(d+1)。

(3)考虑桩侧土摩阻力，单位面积极限摩阻力大小为τ。

(4)考虑桩身自重，桩身任一截面x处轴向力P(x)的表达式为

(2)

式中：γ为桩身混凝土重度；A为桩身横截面积，且A=d2/4；U为桩身横截面周长；x为计算点到坐标原点的距离。

3 屈曲临界荷载解答

3.1 总势能函数的建立

根据图1所示的计算模型，建立超长桩-土体系的总势能方程。桩-土体系的总势能Π由桩身应变能Up、桩侧土体弹性应变能Us、桩顶荷载势能Vp、桩身自重荷载势能Vs、桩侧土体摩阻力荷载势能Wf组成，即

Π=Up+Us+Vp+Vs+Wf。

(3)

(1)桩身应变能Up为

(4)

式中：E为基桩的弹性模量；I为基桩的横截面惯性矩；y为基桩各点水平方向的偏移距离。

(2) 桩侧土体弹性应变能Us为

(5)

式中：当土抗力取常数法时，k=0；当土抗力取C法时，k=0.5；当土抗力选取m法时，k=1。

(3)桩顶荷载势能Vp为

(6)

(4)桩身自重荷载势能Vs为

(7)

(5)桩侧土体摩阻力荷载势能Wf为

(8)

将式(4)—式(8)代入式(3)可得

(9)

3.2 能量法的解答

由图1可知，计算点离原点的距离为x，桩体在x处的水平挠曲位移为y，由于桩底嵌固、桩顶自由，则桩身挠曲位移函数满足几何边界条件，即

(10)

也满足桩身边界条件，即

x=0 ,y′=0 。

(11)

因此，选取桩身挠曲位移函数为

(12)

式中：n为挠曲函数的半波数[11]，取1，3，5,…；Cn为未知常数项。考虑桩-土体系弹性小变形，选取挠曲函数的半波数n=1，此时挠曲函数的未知常数项为1，得到挠曲位移函数，即

(13)

式中C1为待定的常数参量。

由式(13)得到挠曲变形的一阶导数、二阶导数分别为：

(14)

(15)

进一步，将式(13)、式(14)、式(15)代入到式(9)得到桩土体系的总势能，即

Π=Up+Us+Vp+Vs+Wf=

(16)

其中,

(17)

FresnelS(x)和FresnelC(x)均为菲涅尔函数积分，即:

(18)

(19)

由势能驻足原理有

∂Π/∂C1=0 。

(20)

将式(16)代入到式(20)可得

因为C1为非0常数，所以可得临界荷载值为

(22)

4 结果退化与验证

本节从以下3个方面进行结果的退化验证。

(1)如果不考虑桩侧土体摩阻力，且当桩体土抗力常数部分计算长度H=0时，式(22)可退化为文献[18]的解，即

(23)

(2)如果不考虑桩侧土体摩阻力与桩身自重，则式(22)的解可退化为文献[17]的解，即

其中，

(25)

(3)如果不考虑桩侧土抗力，即h=0，且不考虑桩侧土体摩阻力与桩身自重，则临界荷载Pcr为

(26)

式(26)就是一端自由、一端固定时普通压杆稳定时的欧拉公式。

由上述3个解的退化可知，本文所得解均能退化为其他已有研究成果的解析解，说明本文所得解比较可靠。

5 影响因素分析

由理论解可知，超长桩的屈曲临界荷载与桩性质(如桩身挠曲函数、自重、桩长、桩径等)和土体性质(如土抗力形式、桩侧摩阻力、地基土比例系数等)密切相关。因此，本节将综合分析上述因素对超长桩屈曲临界荷载的影响。

验证分析采用控制变量法，当分析某个因素对超长桩屈曲临界荷载影响时，除该因素的参数变化外，其余参数大小都维持不变。取桩土各参数与文献[18]参数一致，即：超长桩位于软塑性黏土中，桩体混凝土为C25，弹性模量为Eh=2.85×104MPa，桩长60 m，桩径1.2 m，计算宽度b=0.9(d+1)=1.98 m，桩身截面周长U=3.77 m，桩身横截面面积A=1.13 m2，桩身抗弯刚度为EI=0.85EhI=2.465×106kN·m2，选取地基土比例系数m=5 000 kN/m4，桩身重γ=25 kN/m3，桩侧土单位面积极限侧摩阻力τ=30 kPa，参考文献[16]，当其他条件不变时，H/h均取0.6计算。

5.1 挠曲函数的影响

由理论解可知， 挠曲函数的常数项项数对桩屈曲临界荷载有着至关重要的影响。 总结发现， 学者们分析时所用的挠曲函数的常数项项数也各不相同， 绝大多数学者在计算桩的屈曲临界荷载时用的挠曲函数常数项项数为1项或者2项，其中文献[11]—文献[13]、文献[17]—文献[18]在计算桩的屈曲临界荷载时用的挠曲函数常数项项数为1，而文献[14]—文献[16]在计算桩的屈曲临界荷载时用的挠曲函数常数项项数为2。

为了研究挠曲函数对基桩屈曲的影响，在计算时分别选用常数项项数为1和2，然后将2种挠曲函数下计算得到的桩的屈曲临界荷载进行对比。其中常数项项数为1时与常数项项数为2的桩屈曲临界荷载计算方法相同，计算得到2种情况下的屈曲临界荷载对比如图2所示。

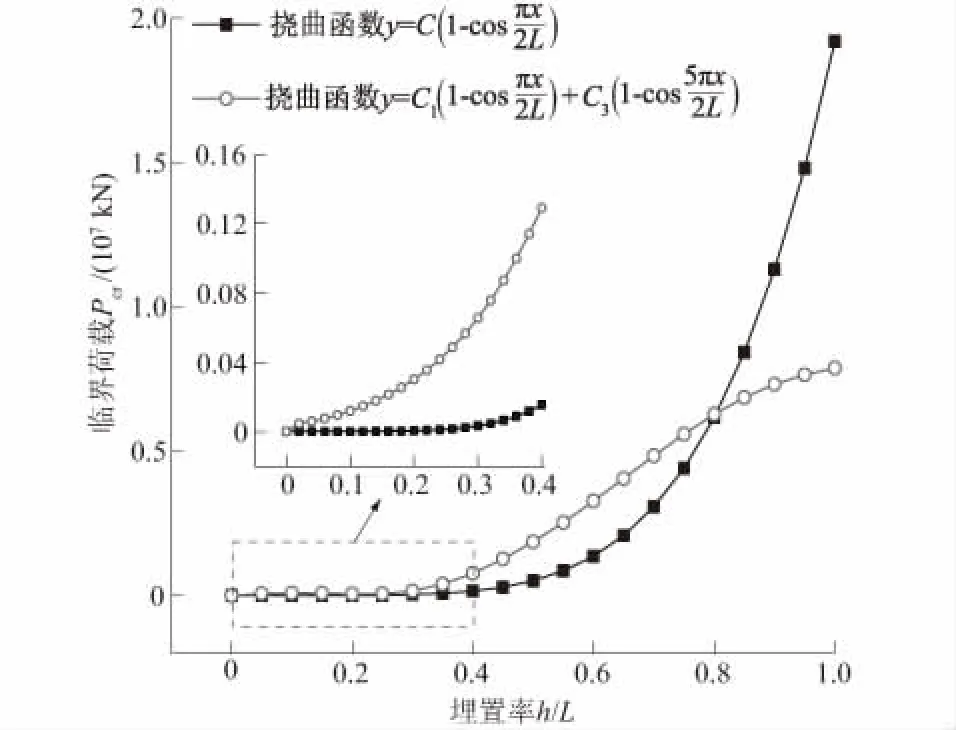
图2 挠曲函数不同时桩屈曲临界荷载对比Fig.2 Influence of flexural function oncritical buckling load of pile

由图2可以看出，当00.8时，挠曲函数常数项项数为1时的临界荷载大于常数项项数为2的临界荷载，并且随着身埋置率h/L的增大，二者临界荷载的差距也越大；当埋置率为1.0时，挠曲函数常数项项数为1时的桩屈曲临界荷载约为常数项项数为2时临界荷载的4.0倍。对比两者的整体曲线可以看出，挠曲函数常数项项数为1时的桩屈曲临界荷载增长速度远远大于常数项项数为2时的增长速度。

因此，在计算超长桩屈曲临界荷载时，为了使得到的屈曲临界荷载更加准确，尽量选择常数项项数较大的挠曲函数。

5.2 土抗力形式的影响

总结已有超长桩屈曲研究发现，在计算基桩土抗力时，到底选择哪种土抗力模式目前还没有得到一致的结论。因此，本文对几种土抗力模式下的桩屈曲临界荷载进行对比分析，分别计算整段土抗力为m法、C法、m法与常数法组合、C法与常数法组合4种情况下桩屈曲临界荷载，得到4种情况下桩屈曲临界荷载与桩身埋置率的关系对比曲线，如图3所示。

图3 土抗力形式不同时桩屈曲临界荷载对比Fig.3 Influence of soil resistance on the criticalbuckling load of pile

由图3可知，当其他参数一定时，桩身埋置率h/L越大，桩屈曲临界荷载也越大。当h/L相同时，土抗力为C法与常数法组合模式下的临界荷载值大于土抗力为C法的临界荷载，但二者差距很小。同样，当h/L相同时，土抗力为m法与常数法组合模式下的桩屈曲临界荷载值大于土抗力为m法的临界荷载，二者差距也很小，几乎一致。由图3还可以看到，土抗力为m法大于土抗力为C法时计算得到的临界荷载，并且随着桩身埋置率h/L的增大，二者差距越来越大；当埋置率为1.0时，用m法计算为用C法计算时的桩屈曲临界荷载值的4.0倍。综合分析结果可以看出，土抗力为C法时小于土抗力为m法时计算得到的桩屈曲临界荷载值，这是因为C法的土抗力小于m法的土抗力，而桩屈曲临界荷载与土抗力的大小成正相关，所以在设计分析超长桩的屈曲临界荷载时，寻找和实际桩所受土抗力模式接近的模型至关重要。

5.3 常数段土抗力长度比值H/h的影响

为了分析常数段土抗力对基桩的影响，以常数段土抗力比值为自变量，保持其他参数不变，计算埋置率h/L分别为0.2，0.4，0.6，0.8，1.0时桩的屈曲临界荷载，得到常数段土抗力计算长度不同时桩屈曲临界荷载的对比曲线，如图4所示。

图4 常数段土抗力计算长度比值不同时桩屈曲临界荷载对比Fig.4 Influence of calculation length of soil resistanceon the critical buckling load of pile by the constantnumber method

由图4可以看出，当桩的常数段土抗力计算长度比值相同且位于0～0.6之间时，且埋置率为1.0时的桩屈曲临界荷载是埋置率为0.8时屈曲临界荷载的3.0倍，埋置率为0.8时的桩屈曲临界荷载是埋置率为0.6时屈曲临界荷载的4.0倍，埋置率为0.6时的桩屈曲临界荷载远远大于埋置率为0.4和0.2时的屈曲临界荷载。由图4还可以看出，当桩的埋置率一定时，桩的常数段土抗力计算长度比值越大，桩屈曲临界荷载越小；并且当常数段土抗力计算长度比值在0～0.6之间时，对应求得的临界荷载值差距比较小；而当常数段土抗力计算长度比值在0.6～1.0之间时，常数段土抗力计算长度比值越大，桩屈曲临界荷载下降越明显；当常数段土抗力计算长度比值为1.0时，整个土抗力计算就是采用的常数段，这个结论恰好验证了学者用常数段土抗力计算桩屈曲临界荷载时比较保守的结论。

5.4 地基土比例系数的影响

为了分析地基土比例系数与桩屈曲临界荷载之间的关系，以地基土比例系数m为自变量，根据理论解计算当桩身埋置率h/L分别为0.2，0.4，0.6，0.8，1.0时的桩屈曲临界荷载值，并进行对比，得到地基土比例系数不同时的桩屈曲临界荷载值对比曲线，如图5所示。

图5 地基土比例系数不同时桩屈曲临界荷载对比Fig.5 Influence of ratio coefficient of foundation soilon the critical buckling load of pile

由图5可以看出，当桩的埋置率一定时，地基土比例系数越大，桩屈曲临界荷载也越大；并且随着地基土比例系数的增大，尤其是对于埋置率较大的时候，桩屈曲临界荷载值增大的趋势越来越明显。这是因为地基土比例系数m与桩侧土体的软硬程度有关，土体越软，m越小，土体越硬，m越大。因此，在其他条件一定时，超长桩在实际工程中可以考虑用在土体比较硬的土层中。

5.5 桩侧单位摩阻力的影响

为了分析桩侧单位摩阻力τ对桩屈曲临界荷载的影响，以桩身埋置率为自变量，并且考虑桩身自重，由式(22)计算τ分别取0，15，30，45，60 kPa时的桩屈曲临界荷载，得到它们的对比曲线，如图6所示。

由图6可以看出，计算时考虑不同桩侧单位摩阻力得到的桩屈曲临界荷载大小几乎相同。为了更加直观地反映它们之间的差值，绘制表1对它们的差值进行对比分析。

图6 桩侧单位摩阻力不同时桩屈曲临界荷载对比Fig.6 Influence of side frictional resistance on thecritical buckling load of pile

由表1可以看出，当埋置率相同时，桩侧单位摩阻力越大，桩屈曲临界荷载也越大；桩侧单位摩阻力对桩的屈曲临界荷载有影响，但影响较小。所以，在进行超长桩屈曲承载力分析时，可以忽略桩侧单位摩阻力对超长桩的影响。

表1 桩侧单位摩阻力不同时的桩屈曲临界荷载Table 1 Values of critical buckling load of pile in the presence of varied side frictional resistance

5.6 桩身自重的影响

为了分析桩身自重对超长桩屈曲的影响，取桩身埋置率为自变量，根据式(23)计算只考虑自重、不考虑桩侧摩阻力时的桩屈曲临界荷载值，根据式(24)计算不考虑桩身自重、不考虑桩侧摩阻力时的桩屈曲临界荷载，得到对比曲线如图7所示。

图7 桩身自重对桩屈曲临界荷载的影响Fig.7 Influence of self-weight on the critical bucklingload of pile

由图7可以看出，不考虑桩身自重时的桩屈曲临界荷载比考虑桩身自重时的桩屈曲临界荷载略小。为了更加直观地反映二者的差异，绘制表2对二者的差值进行对比分析。

表2 考虑与不考虑桩身自重时的屈曲临界荷载比较Table 2 Values of critical load of pile in considerationand in no consideration of self-weight

由表2可得，考虑自重时的桩屈曲临界荷载大于不考虑自重的桩屈曲临界荷载，并且当H/h确定时，二者之间的差值为一定值。随着桩身埋置率的增大，2种条件下桩屈曲临界荷载差值与临界荷载的比值越来越小，当h/L>0.6后，基本可以忽略不计。本文得到的结论与文献[16]的结论基本一致，桩身自重对桩屈曲临界荷载有影响，但影响很小。

5.7 桩长的影响

为了分析桩长对桩屈曲临界荷载的影响，以桩长为自变量，计算埋置率h/L分别为0.2，0.4，0.6，0.8，1.0时的桩屈曲临界荷载，得到桩长不同时桩屈曲临界荷载对比曲线，如图8所示。因为超长桩一般是>50 m的桩，本文选取超长桩的长度范围为50～150 m。

图8 桩长不同时桩屈曲临界荷载对比Fig.8 Influence of pile length on the critical bucklingload of pile

由图8可以看出，桩长越大，桩屈曲临界荷载值也越大，并且随着桩长的增大，尤其是埋置率较大时的桩屈曲临界荷载值增大得越来越明显。如：当埋置率为1.0时，桩长为75，100，125，150 m时的桩屈曲临界荷载为分别为桩长为50 m时屈曲临界荷载的2.5，5，10，15倍。因此，超长桩的屈曲临界荷载与桩长成正相关，在满足其他要求的条件下，在设计与运用超长桩时尽量选择桩长较大的基桩。

5.8 桩径的影响

为了分析桩径对桩屈曲临界荷载的影响，以桩径为自变量，保持其他参数不变，计算埋置率h/L分别为0.2，0.4，0.6，0.8，1.0时的桩屈曲临界荷载，得到桩径不同时桩屈曲临界荷载对比曲线，如图9所示。

图9 桩径不同时桩屈曲临界荷载对比Fig.9 Influence of pile diameter on the criticalbuckling load of pile

由图9可以看出，桩径越大，桩屈曲临界荷载也越大，并且随着桩径的增大，尤其是埋置率较大时的桩屈曲临界荷载值增大得越来越明显。如：当桩的埋置率为1.0时，桩径为1.0，1.5，2.0 m时的桩屈曲临界荷载为桩径为0.5 m时的1.6，2.0，2.4倍。因此，在工程应用超长桩时，尽量选择桩径较大的基桩。

6 结 论

(1) 对于桩身的埋置率，桩身埋置率越大，桩屈曲临界荷载也越大。

(2)对于桩身挠曲函数选取：当h/L<0.8时，桩身挠曲函数常数项为2时的桩屈曲临界荷载要大于挠曲函数常数项为1时的桩屈曲临界荷载；当0.8

(3)对于桩侧土的土抗力：用C法比用m法计算桩屈曲临界荷载时保守，并且无论是用C法还是用m法，常数段土抗力计算长度比值越大，桩屈曲临界荷载越小，计算越保守。

(4)对于桩侧土的性质：桩屈曲临界荷载与地基土比例系数也成正相关，并且无论桩身埋置率取值大小如何，桩侧摩阻力对超长桩屈曲荷载临界荷载影响均很小。

(5)对于桩身自身性质：考虑桩身自重时计算得到的桩屈曲临界荷载值略大，桩屈曲临界荷载与桩长桩径大小均成正相关。