动量与能量守恒下的交叉口安全评价模型

覃 鹏，赵祖菊

(1.深圳市城市交通规划设计研究中心有限公司，广东 深圳 518021；2.贵州财经大学工商管理学院，贵州 贵阳 550022)

0 引言

据世界卫生组织(WHO)发布的《道路安全全球现状报告2015》，全球平均每25 s 就有一人死于交通事故，其中发生在道路交叉口的事故占较大比例[1]。为评估道路交叉口的安全水平，不少学者对安全评价方法、评价指标、影响因素以及改善方法进行研究，提出了基于历史事故统计资料的历史分析法(包括相对事故率法和绝对事故数法)、基于现状因素的回归分析法(包括道路设计因素、道路管控因素及环境因素)以及基于交通冲突技术(Traffic Conflict Technique，TCT)的相关分析法等。

由于TCT在交通安全分析评价中的有效性，在交通安全领域得以被广泛研究和应用。鉴于现有对TCT的研究中存在着诸如定性研究过多、指标选取不合理以及权重系数确定不科学等不足之处，本文在已有研究的基础上引入动量守恒与能量守恒理论，对道路交叉口安全评价模型进行研究。

1 TCT研究简述与动量、能量守恒理论

1.1 TCT的提出及其有效性

TCT 的概念源于航空领域[2]，至20 世纪50年代才于美国开始用于观察车辆之间的空间关系，20 世纪60年代美国GM 实验室首次提出了较为正式的交通冲突的概念[3]。1977年在挪威举行的第一届TCT国际会议上提出TCT的标准定义，即两个或多个道路使用者在一定的时间和空间上彼此接近到一定程度，此时若不改变其运动状态，就有发生碰撞的危险，这种现象称为交通冲突。至此，全球对交通冲突的概念才有一致性的认可[4-5]。此后的不少文献研究极大地推动了TCT 在全球的发展与应用[6-8]。如1978年，文献[6]通过模拟分析交通冲突产生机理，认为交通冲突过程与交通事故发生过程相似，指出TCT能够作为交通事故评价和预测的工具。随着对TCT的研究及应用不断发展，TCT逐渐作为一种高效评价和预测交通安全的非事故统计交通安全评价手段。

关于TCT的一个最基本的问题是有效性验证，即验证基于TCT 的安全分析、评价、预测方法是否具有可靠性，以便能够较为准确地预估交通事故、科学分析交通安全、合理评价安全水平[9-13]。如1986年，文献[10]通过统计学方法比较分析事故和冲突率之间的关系，验证了TCT 的有效性。1990年，国际TCT研讨会倡导以交通冲突技术代替事故统计进行交通安全评价。

TCT的有效性不仅源于其发生机理与交通事故相似，还因其具有样本大、周期短、区域小、信度高等统计学优势特征，被各国学者认为是准交通事故。相较于TCT 方法，基于交通事故统计的传统方法虽具有评价精度高、评价指标逻辑性强等优点，但存在因交通事故的随机性导致的评价周期长、统计工作不完善、评价结果不可靠，以及事故的不可逆性使事故原因分析困难等缺陷。由此，TCT被视为可以代替传统的事故统计方法对交通安全进行快速评价，同时可根据交通冲突的严重程度反映行人的安全感[14]。

1.2 TCT的主要研究内容及不足

TCT的主要研究内容包括冲突类型和冲突机理分析、交通安全评价及基于TCT的方法有效性三个方面[15-28]。已有文献的研究结论都表明基于TCT的交通安全分析、评价及预测方法的有效性[3-5,9-13]。

1）冲突类型研究是根据参与主体及其流向对交通冲突进行分类[11,22]；冲突机理研究主要是通过研究冲突发生的过程探讨其与交通事故发生过程的相似性[4-6,12,15-16]。根据交通冲突的定义，交通冲突实质上是一种既有可能因避让失效转化为交通事故，也可能因为避险有效而避免交通事故的准交通事故，因此其发生过程及机理与交通事故极为相似。

2）交通安全评价研究主要从安全评价方法、指标选取及指标权重确定三个方面展开：已有文献主要对模糊综合评判、层次分析、灰色理论、可拓学、支持向量机、神经网络等方法进行了研究；此外，该项研究不仅提出了冲突时间(Time To Collision，TTC)、后侵时间(Post-Encroachment Time，PET)、冲突数、冲突类型、冲突速度、冲突角度、冲突率以及综合交通冲突率等评价指标[19-23]，还提出了交通设施、车流流向以及交叉口平纵线形设计等影响因素[24-26]。文献[18]以交通冲突率作为评价指标，采用灰色聚类法对右转机动车与行人冲突区域的安全性进行评价；文献[19-20]分别以TTC 和PET 为指标对交叉口机动车-机动车交通冲突的安全性进行分析，并验证了评价指标的有效性；文献[25]利用线性回归及负二项模型分析冲突及严重冲突的影响因素，结果表明左转专用相位、右转车比例及大型车比例为显著影响因素。

3）TCT 的有效性内涵为是否能够通过研究交通冲突分析预测和评价交通安全。基于TCT的方法有效性具有两种释义：一种是发生过程的有效性，另一种是预测结果的有效性[10]。因此不少文献对TCT的预测方法进行了研究[8,11,16]，文献[27]提出了用于交通冲突预测的自适应神经模糊系统模型及灰色模型以预测和评价道路交通安全。

以往关于道路交叉口的TCT安全评价研究仍然存在不足[14-18,21-23,27-28]，主要体现在四个方面：通过冲突角度、冲突速度等定性分析交通冲突的危险程度和严重程度，未进行合理的定量研究；将冲突数、冲突速度以及冲突角度等直接作为严重和危险指标，不能真正反映交叉口交通冲突中能量守恒条件下动能不守恒的转化量是表征交通事故损失的量化值；各指标间权重确定方法的合理性有待商榷；对交通冲突危险程度与严重程度的内涵理解混乱。

1.3 动量与能量守恒理论

动量守恒定律是指如果一个系统不受外力或所受外力的矢量和为0，那么这个系统的总动量保持不变。其不仅适用于宏观物体的低速运动，也适用于微观物体的高速运动，具有普适性。能量守恒定律是指在一个封闭(孤立)系统内，系统总能量保持不变。而能量中的动能(即宇宙中的所有物体因运动所具有的能量，属于标量体系)则通常是不守恒的，当且仅当满足弹性碰撞时，物体或物体所组成的系统的动能总和方可守恒，不具普适性。动能守恒是指如果物体或系统不受力或者所受之力(对于系统，包括外力与内力)矢量和为0，或各力所做元功代数和为0，那么物体或系统的动能保持不变。

根据动量定理，只要满足守恒条件，动量守恒定律总成立，故可以将动量守恒理论应用到交通冲突分析中。根据动能理论，满足动能守恒的弹性碰撞条件一般是指：物体碰撞后，形变能够恢复、不发热、不发声、不发光，故实际中绝大部分物体所组成的系统不满足动能守恒。鉴于交叉口交通冲突不满足弹性碰撞条件，因此本文引入能量守恒并动能不守恒理论建立交叉口安全评价模型对交叉口交通冲突进行分析评价。

对危险程度与严重程度定义不当是已有关于TCT研究中的主要不足，故本文结合动量与能量守恒理论对交通冲突的危险程度与严重程度进行定义，并建立交叉口安全评价模型。交叉口安全评价模型由两部分模型组成：一是在TCT基础上引入动量守恒与能量守恒理论，建立以相对冲突时间为危险程度指标、以动能损失为冲突严重程度指标、以能量均布密度为权重系数，以及基于车道数和车头时距修正冲突数的基础模型；二是基于基础模型以及所定义的元素、向量和矩阵的运算法则，建立交叉口安全水平指标的求解模型。

2 模型参数与假设

本文所建模型需要使用相关参数及规定性用语，还需结合博弈心理学、动力学理论进行必要的合理假设以降低模型复杂程度。

2.1 规定性用语

规定性用语包括：权利转移时刻，即有权与既有权，冲突主体，到达速度与加速度，碰撞前后速度及其角度，冲突距离与转移距离，相对冲突距离与相对冲突时间，序列冲突与主、被动碰撞(冲突)主体。

1）权力转移时刻。指交通流由具有进入交叉口权利转移为仅具有通过交叉口权利的时刻。对于信号控制交叉口，转移时刻是指绿(黄)灯变为红灯的时刻；对主路优先交叉口，转移时刻是指次路交通流发现主路交通流并需要减速或停车让行的时刻；对于环形交叉口，转移时刻是指入环交通流理应让行绕环或者出环交通流的时刻；对于全无管制交叉口，转移时刻是指根据设计速度并结合视距三角确定需要减速避免冲突的时刻。

2）即有权与既有权。即有权是指某些流向车流即将具有驶入交叉口的权利；既有权是指某些流向车流刚刚失去既往具有驶入交叉口的权利。在信号控制交叉口中，即有权与既有权为相邻绿灯相位驶入交叉口的权利。

3）冲突主体。指在冲突交通流中实际存在冲突的参与者，例如在交叉口范围内实际发生冲突的车辆。因此，拥有即有权与既有权的冲突主体分别称为即有权冲突主体(简称即有权主体)和既有权冲突主体(简称既有权主体)。

4）到达速度与加速度。到达速度是指即有权主体与既有权主体在权力转移时的速度。加速度是指权利转移以后即有权主体与既有权主体通过交叉口一般所采用的加速度。

5）碰撞前后速度及其角度。指发生碰撞前后冲突主体的行驶速度，由于速度属于矢量体系，因此具有方向。

6）冲突距离与转移距离。冲突距离是指停车线到冲突点的距离；转移距离是指权力转移时刻既有权冲突主体所处空间位置与该流向停车线的距离。

7）相对冲突距离与相对冲突时间。相对冲突距离是指权力转移时刻即有权主体和既有权主体各自所处位置与冲突点的距离；相对冲突时间是指即有权主体和既有权主体自权力转移时刻起行驶至冲突点各自所需时间，其中，即有权主体的相对冲突时间包括绿灯间隔时间。

8）序列冲突与主、被动碰撞(冲突)主体。序列冲突是指依次根据到达冲突点的时间顺序、速度高低及质量大小来确定的一个有序冲突组合。当到达冲突点时刻不相同时，根据到达时间顺序确定，记为原始有序冲突O，如O(小汽车，自行车)为一个序列冲突(先到达者在前)，表明小汽车先于自行车到达冲突点；当两者同时到达时，需根据速度确定，记为速度有序冲突S，如S(自行车，小汽车)为一个序列冲突(速度低者在前)，表明自行车与小汽车同时到达冲突点，而自行车速度低于小汽车；当两者同时到达且速度大小相等，需根据质量确定，记为质量有序冲突M，如M(摩托车，小汽车)为一个序列冲突(质量小者在前)，表明小汽车与摩托车同时到冲突点且速度相同，而摩托车质量比小汽车小；当两者同时到达且速度和质量都相等时，不需考虑序列冲突中元素位置的前后顺序，记为对等有序冲突E，如E(自行车1，自行车2)或E(自行车2，自行车1)，表明两辆自行车同时到达且速度大小和质量都相等(其中自行车质量包括骑行者质量)。序列冲突中第一个元素为被动冲突主体，第二个元素为主动冲突主体。序列冲突包含冲突主体与冲突顺序，是冲突危险程度、严重程度及权重系数确定的基础。

此外，结合城市道路交叉口各类冲突主体类型(按照参与者类型划分为小汽车、摩托车和助动车、自行车及行人四类)及其流向类型，可以构造一个(10×10)冲突类型矩阵，矩阵包括[(3×3+1)×(3×3+1)-3×3]=91 种可能冲突类型(行人只有人行横道流向)，9种不可能冲突类型(所有右转流向间不存在冲突)，见表1。冲突类型记为(主体类型1，主体类型2)*(流向1，流向2)，定义“*”为关系对应符，流向元素顺序与主体类型顺序一一对应，如(小汽车，自行车)*(左转，直行)，表明冲突类型为左转小汽车与直行自行车的冲突，此冲突类型可以简记为(A,B)*(L,S)，字母含义为所对应的主体类型与流向类型。

需要注意的是，每一种冲突类型可以包含多个子冲突类型(体现为冲突主体流向不相同)。如图1(图中数字表示冲突点及车流与停车线的交点，后文图片含义相同)所示，一种冲突类型包含两个子冲突类型，分别为东、北进口道左转交通流与南进口道直行交通流的冲突类型，但是同样可以记为(A,A)*(L,S)或(A,A)*(S,L)。

因此当按照子冲突类型进行统计时，冲突类型总数由相交道路数量、车道渠化设计和交叉口管控方式等因素共同确定。将序列冲突与冲突类型结合起来，当冲突类型(或者子冲突类型)中主体类型元素是按照序列冲突确定时，则称一个冲突类型为一个序列冲突类型，记所有序列冲突类型的集合为V。一个序列冲突类型包含了冲突主体、冲突主体所在流向、相对冲突时间(速度或者质量)关系以及冲突主体中主动与被动关系。

表1 冲突类型Tab.1 Conflict types

2.2 模型基本假设

为降低模型复杂程度，本文立足实际对模型进行合理假设：

1）权利自利原则：即有权主体不会被动放弃即将进入的权利；既有权主体不会主动放弃既有通过的权利。权利自利原则是交叉口冲突主体之间由冲突转变为交通事故的心理分析理论依据，也是冲突主体行驶状态分析的基础。

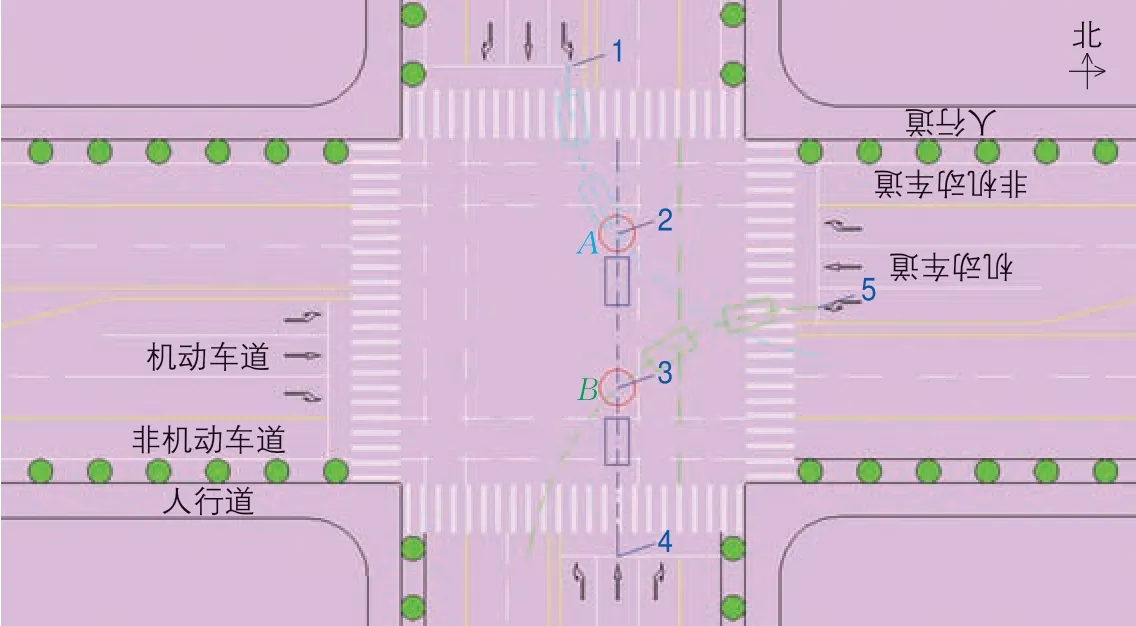
图1 多个子冲突类型Fig.1 Multiple sub-conflict type

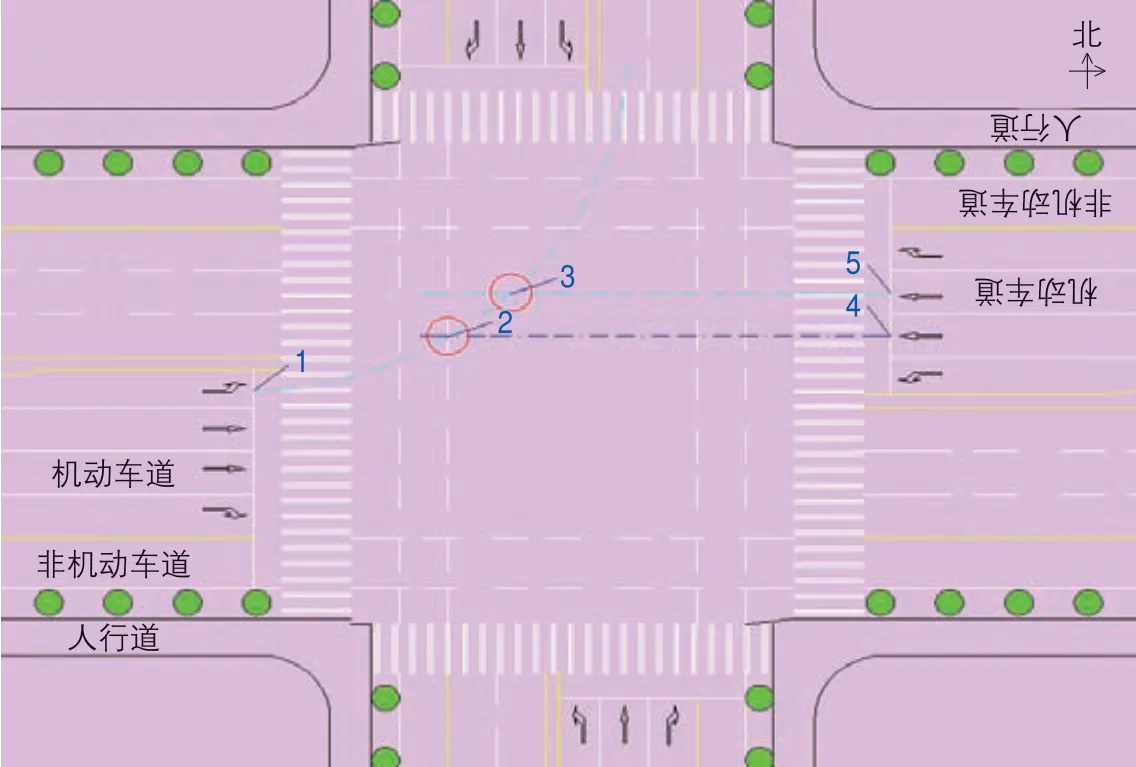
图2 基于车道数的冲突数修正示意Fig.2 Modifying number of conflicts based on number of lanes

2）匀速行驶与匀加速行驶原则：匀速行驶原则是指权力转移前既有权主体匀速行驶至权利转移时所在位置以及权利转移后既有权主体匀速驶向冲突点；匀加速原则是指权力转移后即有权主体匀加速驶向冲突点。从心理博弈角度解释，既有权主体不愿也不能放弃既有的权利，因此需要匀速行驶以示无奈，即有权主体不愿也不该放弃即将具有的权利，因此需要加速行驶以示不满。对冲突主体双方而言，匀加速与匀速行驶是最优策略组合。

3）即时决策原则：指冲突主体都是在通行权利发生转移时(既有权者成为即无权者，既无权者成为即有权者)才进行决策。

4）圆曲线行驶轨迹原则：指左转和右转交通流的行驶轨迹是圆曲线。此假设是通过简化碰撞前冲突主体角度以降低动量守恒分析中不必要的复杂程度。

5）最短距离行驶轨迹原则：指冲突主体在从进口道驶向出口道时，总是沿着行驶路程最短的轨迹。此原则主要针对除行人主体类型以外各类主体的直行流向，因为交叉口总是由于拓宽等原因导致进口道与出口道错位或者进、出口车道数不匹配。

6）车道数折减原则：对于交叉口各冲突主体，当进口道同一流向车道数大于一条时，该流向发生交通冲突的车辆数(即冲突主体数)需要根据车道数进行折减修正。如图2 所示，西进口道设置一条左转车道，东进口道设置两条直行车道，则当西进口道左转车流与东进口道直行车流发生冲突时，东进口道南侧的直行车流给位于北侧的直行车流提供一种庇护，能够有效避免北侧直行车流发生冲突或者降低冲突严重程度与危险程度。

7）车头时距折减原则：某一流向发生交通冲突的车辆数(即冲突主体数)不仅与上述各冲突主体所在流向的车道数有关，还需根据各冲突主体流向上交通流之间的车头时距进行折减修正。如图3 所示，由于绿灯末南进口道直行车流较为离散，车头时距较大，因此该流向发生交通冲突的车辆数并不是绿灯以后冲突车流进行车道数折减后的车辆总数，而是南进口道直行车流中能够与北进口道左转车流发生间隔性冲突的有效冲突车辆数。同时，将各流向有效冲突主体数中每一对冲突主体对应的最大折减冲突主体数之和作为该序列冲突类型的冲突总数，其与车头时距呈现负相关关系。

8）同速行驶原则：指碰撞前后每一类冲突主体的组成部分总是以相同速度行驶。这项原则主要是针对摩托车与自行车等冲突主体类型，如摩托车冲突主体由人与摩托车组成，在碰撞后人因为质量较小有可能获得较大的速度。此原则可以降低动量与能量守恒分析的复杂程度。

2.3 模型参数确定

模型参数主要包括冲突主体质量，到达速度与加速度，冲突距离与转移距离，相对冲突距离与相对冲突时间，以及碰撞前后速度及其角度等。为合理确定各参数的值以科学评价道路交叉口的冲突安全，本文结合TCT相对于传统基于事故统计方法所具有的优势特征给出各参数的确定方法。

1）冲突主体质量。可以根据参与主体的设备参数说明书确定主体质量，摩托车与自行车主体质量包括骑行人员质量。

2）到达速度与加速度。到达速度与加速度可利用TCT的大样本和可重复等优势特征，通过重复观察计算不同交叉口车流实际到达速度与加速度数据，经过统计分析确定各类主体的到达速度与加速度。

3）冲突距离与转移距离。冲突距离根据交叉口几何设计以及车流行驶轨迹确定，其中左、右转车流行驶轨迹通过类似交叉口实际反复统计观察确定，直行车流遵循最短行驶轨迹原则。转移距离通过重复观察不同交叉口不同冲突主体类型的实际转移距离数据，再进行统计分析来确定对应的转移距离。

4）相对冲突距离与相对冲突时间。相对冲突距离与相对冲突时间都可以结合TCT的大样本和可重复等优势特征通过反复观察统计得到。即有权主体的相对冲突距离一般等于冲突距离；既有权主体的相对冲突距离还可以通过冲突距离、转移距离、相对冲突距离三者之间的关系求得。同样，相对冲突时间可以根据相对冲突距离结合到达速度得到。

5）碰撞前后速度及其角度。碰撞前的速度可以根据观察统计得到，也可根据相对冲突距离、到达速度和加速度计算确定，其角度根据行驶轨迹确定。碰撞后速度可以利用TCT的准事故特征，在模拟实验室通过不断改变碰撞主体的质量、碰撞前速度和角度来反复模拟碰撞后的速度及其角度，经统计分析得到。

此外，左右转行驶轨迹的圆曲线半径可以通过图4(图中26 和27表示转弯半径)所示方法得到。右转车流与左转车流行驶轨迹的圆曲线半径Ra取值为线段AC与线段BC的长度最大值，即Ra=MAX(AC,BC)。A和B是相应车道的宽度中点，且在停车线上或者停车线延长线上，即左转车流或者右转车流轨迹的起终点，C点为交点。

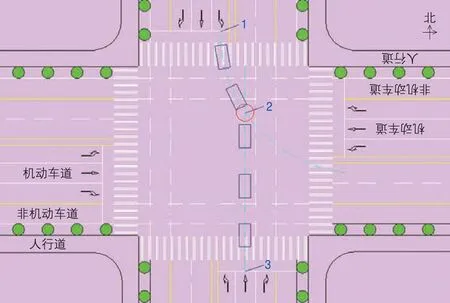
图3 基于车头时距的冲突数修正示意Fig.3 Modifying number of conflicts based on headway

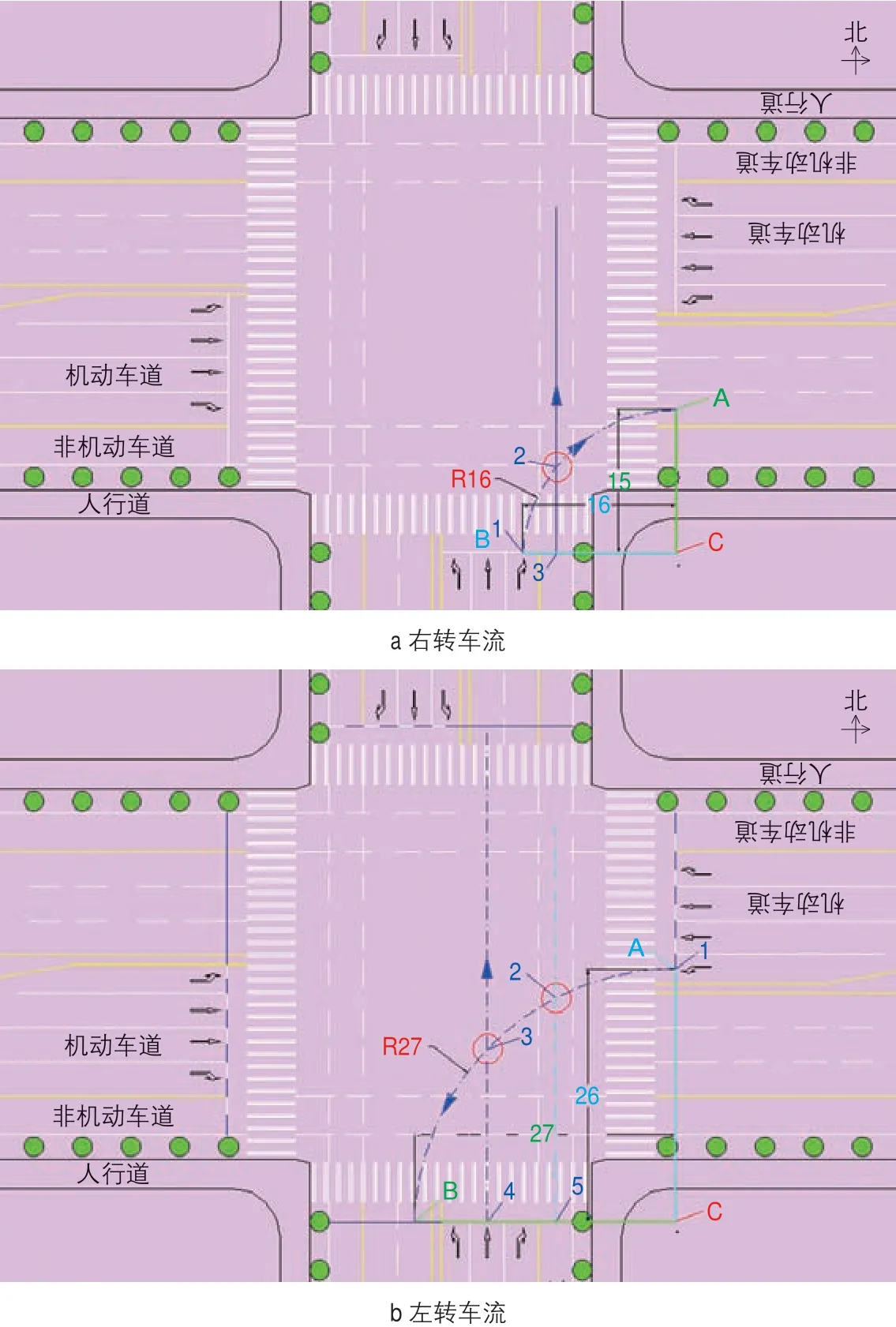
图4 转向车流行驶轨迹半径确定Fig.4 The radius of right-turn and left-turn

3 交叉口安全评价基础模型

道路交叉口交通冲突的危险程度与严重程度与车辆行驶速度密切相关。由于以往研究文献中通常直接以冲突速度、冲突角度、冲突数、冲突距离、冲突时间等表征冲突危险程度和严重程度，并不能真实分析速度在交通冲突中的关键性[15-17,21-22,27-28]。基于此，本文先对交通冲突危险程度与严重程度进行科学定义：危险程度是指交通冲突转变为交通事故的可能性，严重程度是指交通冲突成为事故时所导致的伤害程度。因此，越容易转化为交通事故的交通冲突越危险，能量转化值越大的交通冲突越严重。

3.1 冲突危险程度分析模型

将既有权与即有权冲突交通流在交叉口内行驶轨迹重叠的中心点称为交通冲突点。如果既有权冲突交通流与即有权冲突交通流在权利转移时均决策开始匀加速驶向冲突点，则冲突可能转化为交通事故，这种可能性与冲突危险性有关。为表征冲突的危险性，本文将相对冲突时间差作为危险程度测度值。相对冲突时间差是指既有权冲突交通流与即有权冲突交通流各自相对冲突时间之差的绝对值。此绝对值越小，表明发生交通事故的可能性越大，也就越危险，反之亦然。

图5 冲突交通流示意Fig.5 The conflict traffic flow

如图5所示，对于第k种(k∈V,V=(1,2,3,…,K)，K表示进出口所有序列冲突类型的总数)序列冲突类型(包含子冲突类型)，冲突交通流的即有权交通流中第i个冲突主体与既有权交通流中第j个冲突主体是一对冲突主体(记为i,j)，i=j=(1,2,3,为各序列冲突类型中冲突主体对的总数。i和j的到达速度分别为Snki和Sekj，加(减)速度分别为Anki和Aekj；相对冲突距离分别为Dnki和Dekj；相对冲突时间依次为Tnki和Tekj；相对冲突时间差为∇Tki.j。

以南进口道直行交通流与北进口道左转交通流为例，直行交通流为既有权交通流、左转交通流为即有权交通流，根据运动力学理论，则有：

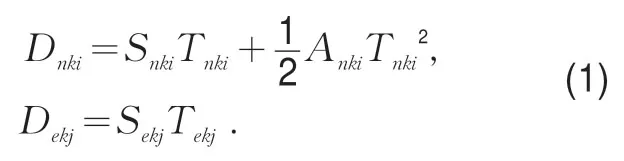
对式(1)进行变形，得到

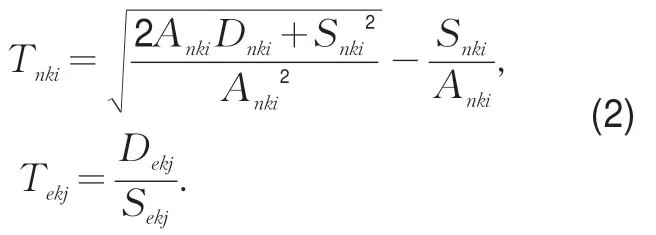
据式(2)可求得相对冲突时间∇Tki.j：

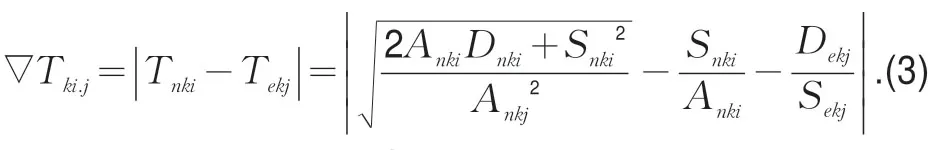
对式(3)分三种情形进行讨论：

1）情形一：Tnki=Tekj。

此情形表明即有权主体与既有权主体同时到达冲突点，在不采取避让的情况下一定会发生头对头的碰撞事故。因此当∇Tki.j=0，冲突十分危险。

2）情形二：Tnki＞Tekj。

此情形表明既有权主体先于即有权主体到达冲突点，在不采取避让措施的情况下，即有权主体的头部一定与既有权主体头部以后的部位发生碰撞事故，相当危险。

①当Anki,Aekj,Dnki和Dekj等均为定值时，可知∇Tki.j是Snki和Sekj的复合函数，对∇Tki.j关于Snki和Sekj分别求偏导数，则有：

根据式(4)知∇Tki.j是Sekj的增函数，即当既有权主体速度Sekj越低时，其在冲突区域滞留时间越长，则其被即有权主体碰撞的可能性就会增大，即反推出∇Tki.j减小；反之，当Sekj越大时，既有权主体在冲突区域滞留时间越短，则其被即有权主体碰撞的可能性减小，即反推出∇Tki.j增加。对于Snki，令：

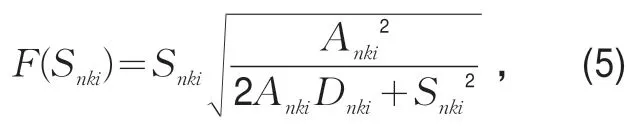
由于F(Snki)与∇T1ki.j关于Snki具有相同的函数单调性，可以通过对F(Snki) 关于Snki求导，把握∇T1ki.j关于Snki的关系，进一步把握∇Tki.j关于Snki的关系，则有

事实上，由于Snki是即有权交通流在权利转移时的初速度，通常取值非常小(甚至为0)。由于一般车辆10 s 可以加速到100 km·h-1，因此其加速度可达2.78 m·s-2，考虑到驾驶舒适性，取Anki=2 m·s-2。根据交叉口几何设计，Dnki一般大于10 m。因此，只有成立，即当即有权主体的Snki越高时，∇Tki.j就越小，其主动碰撞既有权主体的可能性越大，也就越危险，反之亦然，符合一般实际情况。

②当Anki,Aekj,Snki和Sekj等均为定值时，可知∇Tki.j是Dnki和Dekj的复合函数，对∇Tki.j关于Dnki和Dekj分别求偏导数，则有：

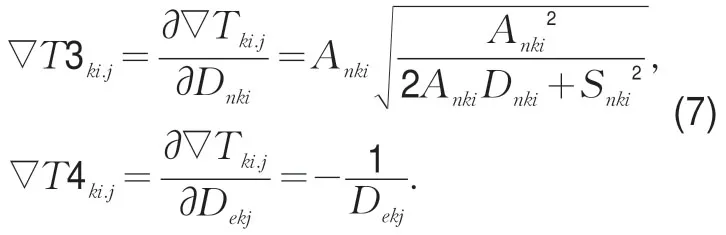
由式(7)知， ∇T3ki.j是Dnki的减函数且恒大于0，故∇Tki.j是Dnki的增函数。即当即有权主体的Dnki越大时，∇Tki.j就越大，此时其主动碰撞既有权主体的可能性越小，也就越安全，符合一般实际情况。

同样，由式(7)知，∇T4ki.j恒小于0，故∇Tki.j是Dekj的减函数。当Dekj越小时，既有权主体在冲突区域滞留时间越短，则其被即有权主体碰撞的可能性就越小，可反推出∇Tki.j越大；反之，当Dekj越大时，既有权主体在冲突区域滞留时间越长，则其被即有权主体碰撞的可能性越高，可反推出∇Tki.j越小。

3）情形三：Tnki＜Tekj。

此情形表明即有权主体先于既有权主体到达冲突点，在不采取避让措施的情况下，既有权主体的头部一定与即有权主体头部以后的部位发生碰撞事故，相当危险。

对于情形三的分析与情形二类似，分析结果则刚好相反，即∇Tki.j是Sekj的减函数；∇Tki.j是Snki的增函数；∇Tki.j是Dnki的减函数；∇Tki.j是Dekj的增函数。

于是，令危险程度Rki.j=∇Tki.j，根据以上计算式得到第k种序列冲突类型的各对冲突主体的相对冲突时间差(即危险度)，便可得到第k种序列冲突类型的危险度向量Rk，再依次对K个序列冲突类型计算危险度向量，最终得到一个序列危险程度矩阵R。

3.2 冲突严重程度分析模型

本文采用动量守恒与能量守恒条件下动能不守恒的动能转化量作为表征交通冲突严重程度的度量值。在第k种序列冲突类型的冲突交通流中，设即有权交通流中第i个冲突主体与既有权交通流中第j个冲突主体的质量分别为Pnki和Pekj；到达速度分别为Snki和Sekj；发生冲突前的方向分别为dnki和发生冲突后速度分别为发生冲突后的方向分别为碰撞过程中动能转化量为∇Eki.j。

根据动量守恒定律以及动能守恒定律，有

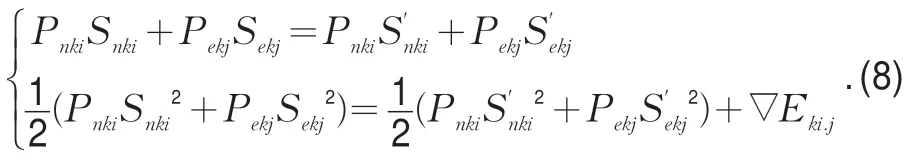
由于冲突演变为交通事故时，会导致即有权交通流中第i个冲突主体与既有权交通流中第j个冲突主体的运转状态发生改变(主要是指速度的大小与方向的改变，不考虑冲突导致的质量改变)，故分别将第i个冲突主体与第j个冲突主体发生冲突前后的动量进行南北向和东西向分解，根据矢量加法三角形原则，分别对南北向和东西向动量进行求解。

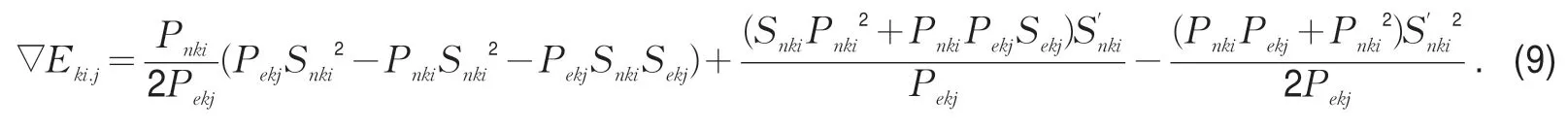
令∇Eki.j=∇E1ki.j+∇E2ki.j，则∇E1ki.j=

由式(9)可知，当Pnki,Pekj,Snki,Sekj,等均为定值时，动能转化量∇Eki.j仅与及其方向有关，即∇Eki.j仅与∇E2ki.j有关。于是，对∇E2ki.j关于求偏导数，得到可见，是关于的减函数。当且仅当此时∇Eki.j与的增减方向与相同。当且仅当，此时∇E与∇E2 取得最大ki.jki.j值。当且仅当时，此时∇E与∇E2 的增减方向与ki.jki.j相反。

于是，令严重程度Hki.j=∇Eki.j，根据以上计算得到第k种序列冲突类型的各对冲突主体的动能转化量(即严重度)，便可得到第k种序列冲突类型的严重度向量Hk，再依次对K个序列冲突类型计算严重度向量，最终得到一个序列严重程度矩阵H。

3.3 冲突权重系数分析模型

选取交通冲突的严重程度(即严重性)和危险程度(即危险性)作为评价指标，其中危险程度作为控制性指标，严重程度作为参考性指标。然而上文确定的危险度和严重度不能直接作为安全水平的评价指标，因为交叉口冲突的危险度和严重度还与不同序列冲突类型及其冲突主体对的冲突数和权重有关。在以往研究中，指标权重的确定方法大多采用灰色聚类、模糊聚类以及层次分析法。鉴于这些方法不能较好地反映速度在交通冲突中的关键性作用、表征速度所隐含的发生碰撞事故的危险性以及量化速度所携带的动能对碰撞事故主体伤害的严重性，因此，本文基于动能损失转化值确定权重系数。

根据前文分析，依据质量将交叉口交通冲突主体分为小汽车、摩托车和助动车、自行车及行人四类。根据动能理论，当动能转化量∇Eki.j一定时，主体受伤害严重程度取决于所承受动能转化量∇Eki.j的被动冲突主体的有效质量。因此将能量均匀分布密度(简称“能量密度”)作为相对权重系数，能量密度是指各序列冲突类型中动能转化量与被动冲突主体的质量之比。第k种序列冲突类型中第i与j冲突主体的动能转化量为∇Eki.j，序列冲突类型的被动冲突主体的质量为Pki.j，则其能量密度令权重系数进而得到第k种序列冲突类型的权重向量Wk，再依次对K个序列冲突类型计算权重系数向量，最终得到一个序列权重系数矩阵W。

3.4 交叉口冲突数计算模型

冲突的危险性和严重性与不同序列冲突类型及冲突数有关。冲突数由冲突主体对构成，在不考虑车道数和车头时距修正时，每一对冲突主体即为一次冲突；当考虑车道数和车头时距修正时，冲突数为修正后的冲突数，由实际调查确定。记i.j的冲突主体的冲突数(进行车道数和车头时距修正后)Cki.j=MAX(CTk.i,CTk.j),k∈V,i=j=1,2,3,…,U；将Cki.j求和得到第k种序列冲突类型的冲突数向量将CTk求和得到交叉口所有序列冲突类型的冲突数矩阵式中：U为各序列冲突类型中冲突主体对的总数；CTk.i和CTk.j分别为第k种序列冲突的即有权车流中冲突主体i的可能冲突数和既有权车流中冲突主体j的可能冲突数，均为进行车道数和车头时距修正之后的冲突数；C为一个交叉口所有序列冲突类型的实际冲突数，包含了所有子冲突类型。

4 交叉口安全水平指标求解模型

交叉口的冲突安全水平评价重点是要知道交叉口冲突的危险性和严重性，危险性是度量冲突转化为交通事故的可能性，严重性是表征冲突演变为事故时的伤害严重程度。因此，通过计算危险度和严重度的向量和矩阵，并计算其对应的权重系数向量和矩阵，在考虑冲突数的情况下评价交叉口的冲突安全水平。评价分为五个层级：冲突主体对元素层、序列冲突类型平均层和总体层及交叉口平均层和总体层。

1）冲突主体对元素层的目标是评价交叉口每一种序列冲突类型的每一对冲突主体的安全水平，可以全面分析交叉口冲突安全水平的分布。

对危险度与严重度的表征指标，基于权重系数和冲突数定义运算法则“⊗”进行求解，表示对应元素相乘。则每对冲突主体的危险度指标Rpki.j=Rki.j⊗Wki.j⊗Cki.j=Rki.jWki.jCki.j，Rpki.j越大，冲突越危险。同样每对冲突主体的严重度指标Hpki.j=Hki.j⊗Wki.j⊗Cki.j=Hki.jWki.jCki.j，Hpki.j越大，冲突越严重。

2）序列冲突类型平均层的目标是评价每一种序列冲突类型中所有冲突主体对的平均安全水平，以把握每一种序列冲突类型的平均安全程度。

定义运算法则“⊕”，表示对每个向量元素求其均值并将均值相乘。则每种冲突类型的危险度指标Rpkp=Rk⊕Wk⊕Ck越大，冲突越危险。同样每对冲突主体的严重度指标Hpkp越大，冲突越严重。

3）序列冲突类型总体层的目标是评价每一种序列冲突类型中所有冲突主体对的总体安全水平，以把握每一种序列冲突类型的总体安全程度。

定义运算法则“⊗⊕”，表示每个向量中对应元素相乘之后再对应相加。则每对冲突主体的危险度指标越大，冲突越危险。同样每对冲突主体的严重度指标Hpct=越大，冲突越严重。

4）交叉口平均层的目标是评价交叉口所有序列冲突类型中所有冲突主体对的平均安全水平，以把握所有序列冲突类型中所有冲突主体对的平均安全程度。

定义运算法则“⊕⊕”，表示对每个矩阵中基于某一类序列冲突的对应元素相加求平均值之后再将平均值相乘。则每对冲突主体的危险度指标Rpp=R⊕⊕WRpp越大，冲突越危险。同样每对冲突主体的严重度指标Hpp=H⊕⊕W⊕⊕C=越大，冲突越严重。

5）交叉口总体层的目标是评价交叉口所有序列冲突类型中所有冲突主体对的总体安全水平，以把握所有序列冲突类型中所有冲突主体对的总体安全程度。

定义运算法则“⊗⊗”，表示对每个矩阵中基于某一类序列冲突的对应元素相乘之后再对应相加。则每对冲突主体的危险度指标Rpt越大，冲突越危险。同样每对冲突主体的严重度指标Hpt=H⊗⊗W⊗⊗C=越大，冲突越严重。

交叉口的冲突安全水平评价包括两个方面，即冲突的危险性和严重性。将危险度作为控制性指标，严重度作为参考性指标，先根据危险度确定交叉口的冲突危险性，再根据严重度判断交叉口的冲突严重性。

5 结语

本文在TCT的基础上引入动量守恒理论与能量守恒并动能不守恒理论，建立满足各种管控方式的交叉口冲突安全水平评价模型。通过动量守恒与能量守恒理论，定义了用于评价交叉口安全水平的危险性、严重性、权重系数、冲突数以及序列冲突类型和冲突类型等指标，并建立了求解危险性、严重性、权重系数以及冲突数所对应的元素、向量及矩阵的计算模型，同时定义了针对不同安全水平层级的元素、向量以及矩阵运算法则，可灵活求解对应层级的安全水平。未来基于TCT的交叉口安全研究应重视考虑动量守恒和能量守恒并动能不守恒等理论的引入运用。