Mathematica软件支持下等量同种电荷类电场的定量分析

董 平

(南京师范大学第二附属高级中学 江苏 扬州 211900)

电场由于有着看不见、摸不着的抽象特点，所以教材[1]及教师在介绍、讲解这一部分时，往往以定性分析大小关系居多，定量得出精确结果居少，使得物理这样一个原本很严谨的学科，多少留下了一些遗憾.同时，学生在学习电场时也存在诸多疑惑.笔者发现借助于数学Mathematica软件，利用导数和微元法(即高等数学中的“微积分”)定量计算，能够优化上述问题.

Mathematica是美国Wolfram研究公司开发的符号计算系统，具有高精度的数值计算和强大的数学计算功能，Mathematica8及更高版本新增了“自由格式语言输入”功能，不需要操作者熟悉众多的计算机编程语言和方法，更适合在中学教师和学生中推广应用.本文介绍在该软件的支持下，对等量同种电荷连线的中垂线上和均匀带电圆环轴线上的场强定量分析过程.

1 等量同种电荷连线中垂线上的场强

1.1 定性分析

真空中的两个等量同种电荷电场分布情况大致如图1所示，中垂线上的场强变化情况我们在教学过程中常做这样的定性分析：两电荷连线中点处场强为零，无穷远处场强也为零，其他位置场强不为零.故在中垂线上，从图1中O点开始，沿x轴正方向场强先增大，再减小，中间某处存在场强的最大值.然而，最大值的位置究竟在哪呢？我们可以结合图1作如下的定量计算.

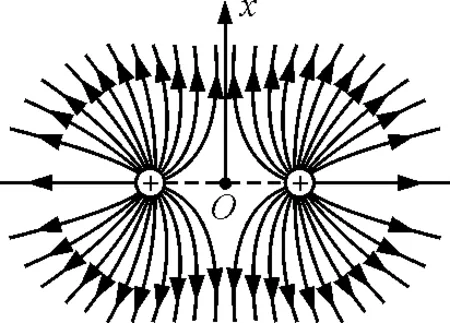
图1 等量同种电荷电场的分布

1.2 物理建模及Mathematica定量计算

以两个等量带正电的点电荷为模型，如图2所示.

图2 两个等量同种电荷模型

A和B是两个带电荷量均+Q的点电荷，间距为2l，它们连线的中点为O，P点是中垂线上的任一点，AP和AB的夹角为θ.则任一点P处场强为

E=EAsinθ+EBsinθ=

(1)

为定量分析电荷量Q和间距2l这两个参量对场强E的影响，使用Manipulat(交互运行)函数，在此取Q∈[0,+5×10-8C]，l∈[0,+0.2 m].对函数的可视化求解是Mathematica最大的优点之一，为直观展示场强E随位置x的变化情况，使用Plot(绘图)函数，可进行如下编程：

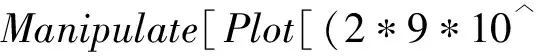
运行结果如图3所示，与前文定性分析结果一致.

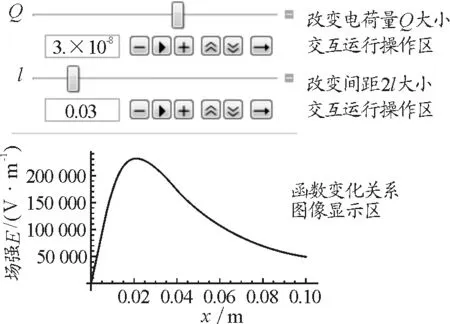
图3 Mathematica输出的操作区和场强变化图像

正如前文定性分析所述，场强E确实存在最大值.由数学知识可知，导函数为零的点即为原函数的极大值处.对式(1)求E关于x的导数并化简，由于计算过程较为复杂，在此借助于Mathematica软件.使用FullSimplify(完全简化)函数和D(给出偏导数)函数，可进行如下编程：

运行结果为

(2)

令式(2)E′=0，解得

最大值的位置与电荷量Q无关，仅取决于间距2l.

1.3 定量结论

综上所述，等量同种电荷连线中垂线上的场强变化如图4所示.

图4 等量同种电荷连线中垂线上的场强

2 均匀带电圆环轴线上的场强

2.1 物理建模及Mathematica定量计算

以电荷量分布均匀的金属圆环为模型如图5所示.圆环带电荷量为Q，半径为R，O点为圆环的圆心.因圆环不可视为点电荷，所以在此不可直接用库仑定律来分析其轴线上任一点P处的场强.

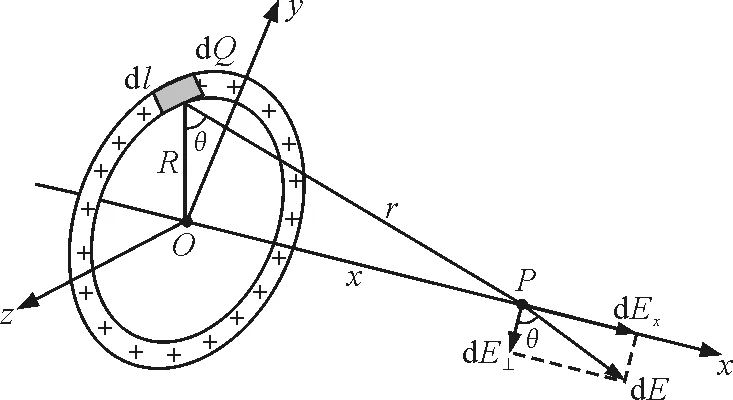
图5 均匀带电圆环模型

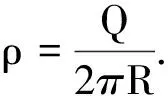
由于电荷分布的对称性，圆环上各电荷元对点P处激起的场强dE的分布也具有对称性.由图5可见，dE在垂直于x轴方向的分量dE⊥相抵消，而沿x轴方向的分量dEx相叠加.且

(3)

对这些分量累积求和有(即积分，计算复杂的积分可借助于Mathematica中的Integrate积分函数)

(4)

取Q=3×10-8C，R=0.1 m，使用Plot(绘图)函数，可进行如下编程：

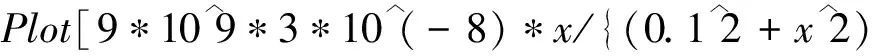
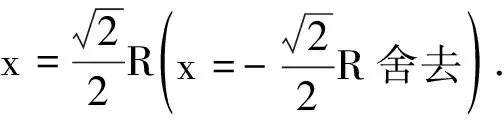
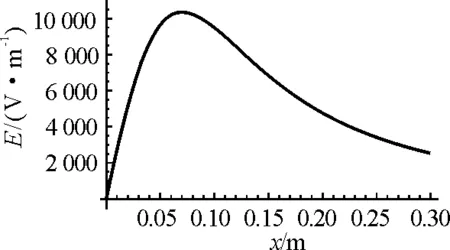
图6 均匀带电圆环轴线上的场强

2.2 定量结论

3 结束语

本文的导数、积分看似复杂，可能对于我们高中物理教师而言，略有困难.但在Mathematica软件的支持下，使得复杂的数学计算得以解决.这对我们深入研究某些物理规律、消除学生的思维障碍有着很大的帮助.同时在由定性分析到定量计算的过程中，既实践了物理学科的严谨，也提升了高中生的物理核心素养.