三标度AHP-TOPSIS评判模型在施工方案绿色度比选中的应用
董彦辰,姜安民,邹品增,倪 佳
(1.湖南城建职业技术学院, 湖南 湘潭 411100;2.中南林业科技大学 土木工程学院, 湖南 长沙 410004;3.湖南大学 土木工程学院, 湖南 长沙 410082)
近些年,随着国家对基础设施建设投入的加大,建筑活动愈加频繁。在建筑施工过程中,除了使自然资源大量消耗外,还会对环境产生诸多不利影响。如:土壤污染、空气污染、水污染等问题都亟待解决,这些问题直接影响到了我国经济的可持续发展。基于环境保护的理念及国家可持续发展战略的主导思想,“绿色施工”的理念被提出,并逐渐开始对其重视,国家相关部门先后发文、并颁布了多部相关规范。如:《绿色施工导则》建质[2007]223号、《建筑工程绿色施工评价标准》(GB/T 50640—2010)、《绿色建筑评价标准》(GB/T50378—2014)、《建筑工程绿色施工规范》(GB/T50905—2014)等。绿色施工是一个要求很高的系统工程[1],在整个施工过程中需要让各环节实现一体化、信息化,对施工过程中采用的技术及组织管理的水平都有很高要求。在组织绿色施工的过程中,除了有相关规范的指导,还应该建立完善的绿色施工评价指标体系,科学的选取评价方法,这样才能更好的了解拟建、在建或已完工程的“绿色度”。
目前,我国针对绿色施工的研究中以理论研究为主。如:张晶波等[2]通过建立模糊综合评价模型,对某省图书馆进行绿色施工评价。闫志刚等[3]建立绿色综合评价指标体系,利用突变级数法对绿色施工进行研究。何亚伯等[4]基于复合物元与信息熵建立绿色施工评标模型。鲍学英等[5]采用灰色聚类法对铁路绿色施工等级进行评价研究等。
本文从施工方案比选的角度进行分析研究,这样有助于选出“绿色度”相对较高的施工方案,可以在前期对绿色施工的实现进行把控。通过建立完善的评价指标体系,构建三标度AHP-TOPSIS评判模型,对所有施工方案进行排序,进而选出最优,即“绿色度”最高的施工方案。现行绿色施工评价规范主要是进行事后评价,暂无针对施工方案“绿色度”评价的具体方法,本研究填补了该空白,为绿色施工的后续研究提供了借鉴。
1 施工方案“绿色度”评价指标体系
绿色施工是由传统的施工模式发展而来,因此,绿色施工与传统施工有着共同的目标,即“质量目标、进度目标、成本目标”。在传统的施工过程中,更重视三大目标的实现,对资源消耗、环境的影响等方面未做过高要求。基于可持续发展的理念,需在实现三大目标的基础上充分考虑节能减排、施工管理水平的高低、对环境污染情况等方面。因此,在施工方案“绿色度”比选的过程中需充分考虑上述因素。
建立科学、完善、客观、可操作性强的评价指标体系是进行施工方案“绿色度”比选的基本保障,综合上述分析,参考《绿色施工导则》建质[2007]223号、《建筑工程绿色施工评价标准》(GB/T 50640—2010)等相关规范,及文献[1-3,5],建立施工方案“绿色度”综合评价指标体系,其中包括4个一级评价指标、13个二级评价指标,具体见下表1。

表1 施工方案“绿色度”综合评价指标体系
2 施工方案“绿色度”评价模型
2.1 三标度AHP
在确定评价指标权重的过程中AHP应用较为广泛,传统的AHP为九标度,在应用的过程中如果出现较为严重的不一致现象则需要重新建立判断矩阵,此过程较为繁琐,需要反复迭代,直到通过一致性检验[6]。三标度AHP省略了一致性检验的步骤,在评价指标重要性比较的过程中较为容易做出判断,该方法简便快捷,且精确度可以满足计算要求[7-9]。具体操作如下:
(1) 建立初始判断矩阵K,计算重要性排序指数ri
(1)
式中:kij为i因素与j因素的重要程度比较值,其量化规则见表2。

表2 三标度AHP量化规则
(2)
式中:ri为矩阵K中第i行元素之和。
(2) 建立判断矩阵A
(3)

(4)
(3) 权重计算
(5)
(6)
进而,得到主观权重向量:
w=(w1,w2,w3,……,wn)
(7)
2.2 三标度AHP-TOPSIS评判模型
TOPSIS法,即逼近理想解排序法。对研究对象的优劣进行比较、排序,其基本思想是通过研究对象到正理想解与负理想解的距离来进行评判[10]。各指标达到最优的即为正理想解,这个最优解可以认为是个虚拟解,负理想解与其恰好相反。TOPSIS法根据评判对象与理想化目标的接近程度进行排序,对现有对象做出优劣的相对评价[11],与正理想解最为接近的评判对象,则为最优值,最差值即为与正理想解最远的评判对象。在多目标决策分析中TOPSIS 法应用较为广泛,基于三标度AHP构建TOPSIS评判模型,具体操作见图1。

图1三标度AHP-TOPSIS评判模型操作流程
(1) 建立初始判断矩阵。基于研究需要,并结合工程实际情况,建立施工方案集P={P1,P2,……,Pm},各个施工方案评判指标集r={r1,r2,r3,……,rn},根据评判指标集,建立初始判断矩阵如下:
(8)
式中:rij代表第i个施工方案的第j个评判指标初始判断值,i∈[1,m],j∈[1,n]。
(2) 决策矩阵标准化。收益性与消耗性是评判指标的一种划分,对于收益性指标,其数值越大越好,对于消耗性指标,则为越小越好。通常各评判指标量纲和量纲单位差别较大,不具备可比度,为了解决这种现象,需采用归一化方法处理原始数据,得到标准化决策矩阵,具体如下:
(9)
(10)
(11)
(3) 加权标准化决策矩阵。矩阵B的列向量与三标度AHP所求各指标层次总排序权重W相乘,得到加权标准化决策矩阵F如下:
(12)
(4) 分析贴近度。对于收益性指标集J1取各方案中该指标的最大值,即为正理想解;各指标的最小值即为负理想解,消耗性指标集J2的取值与之相反,具体如下:
(13)
(14)
式中:F+表示为正理想解,F-表示为负理想解。各评价方案与理想解的距离用下式表示:
(15)
(16)

贴近度分析见下式:
(17)

3 工程实例
(1) 工程概况。A市大型客运中心(西区)大型基坑工程位于东朝阳路以南、西侧为房山路、东临工业路、南面靠江,是目前第四代客运中心,采用筏板基础+桩基的基础形式。本工程设计为地下三层,平面为250 m×120 m的矩形,开挖深度为13.0 m~13.5 m。施工场地浅部地下水为潜水型,主要由地表的江水及大气降水补给。对施工场地进行勘探,由上到下分别为杂填土、粉质黏土、黏土、中砂、泥岩。
(2) 建立初始判断矩阵。大型基坑工程施工风险较高[13-14],在保证基坑施工安全的前提下,基于绿色施工理念,结合工程实际情况,综合考虑土方开挖及支护方式,拟定了四个基坑施工方案,P={P1,P2,P3,P4},每个方案评判指标集r={r1,r2,r3,……,r13}(见表1)。通过专家对各评价指标进行评分,建立初始判断矩阵,在本研究中采用9分制,具体评分细则,见表3[2-3,15-17]。由于本评价为事前评价,因此很多指标无法获得实测值,需根据施工方案的具体内容及保证措施,充分论证其可实现性后给出分值。
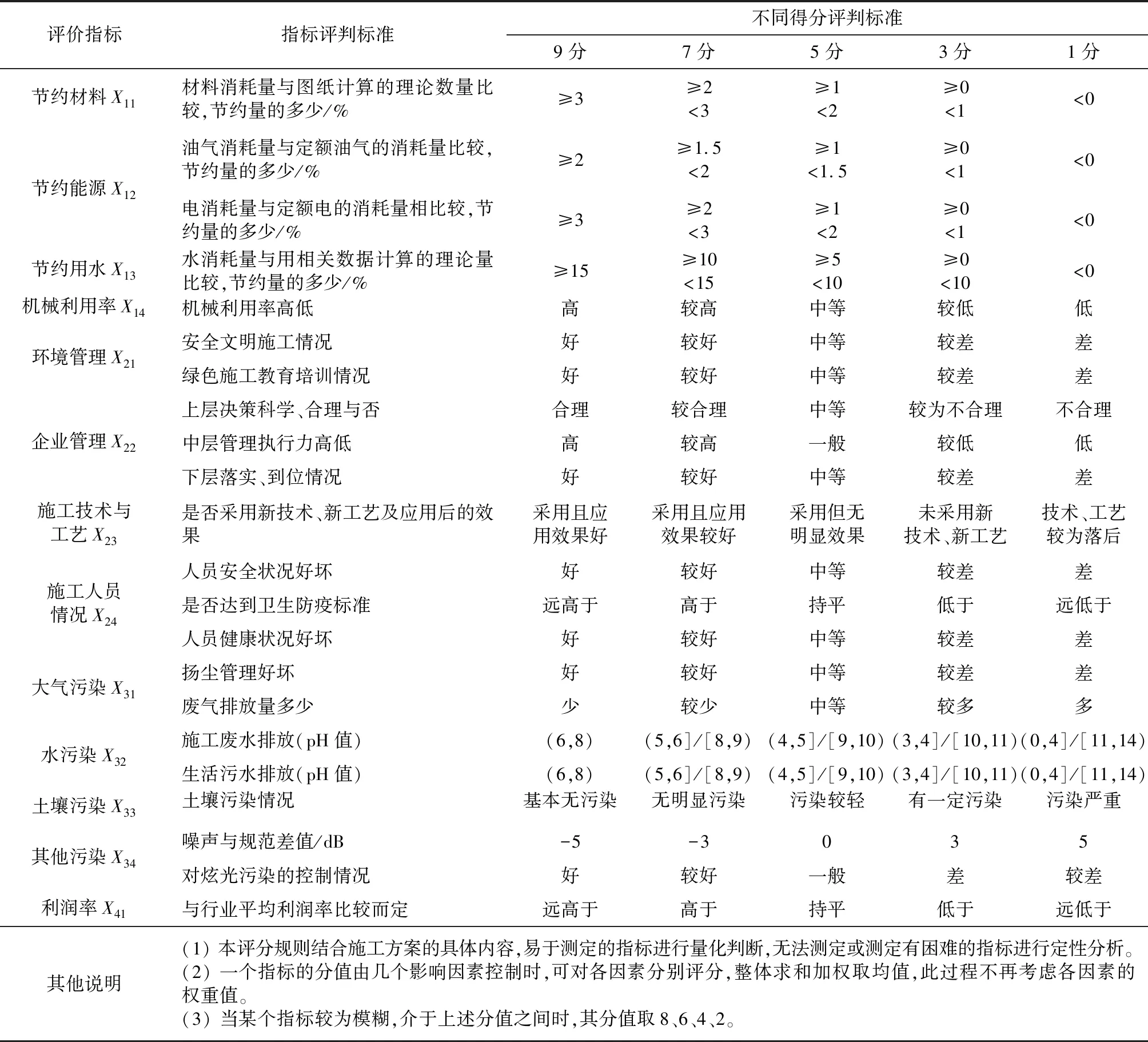
表3 指标评分细则
本工程邀请10位技术、经济方面专家对各方案的评价指标进行打分,每个指标最后的分值根据10位专家所打分数加权平均、向上取整得出,具体评分结果(以方案P1为例),见表4。

表4 评分结果(P1)
根据评分各方案评分结果,建立初始判断矩阵如下:
R=(rij)m×n=

(3) 加权标准化决策矩阵
① 确定指标权重。将X中的4个一级评价指标建立初始判断矩阵K,见表5。

表5 一级评价指标相对于X的初始判断矩阵
根据初始判断矩阵结果,建立判断矩阵A,并求得一级评价指标权重,见表6。
采用此方法,求得所有二级指标权重,及层次总排序权重,见表7。
② 加权标准化决策矩阵。本研究直接采用分值代替指标具体取值,因此可不进行归一化处理,则加权决策矩阵如下:

表6 一级评价指标相对于X的判断矩阵及权重

表7 二级指标权重及层次总排序权重

(4) 贴近度分析。根据上式得正理想解和负理想解如下:
F+=(1.25680.49040.42910.11270.05320.16480.29750.36451.05070.5103
2.05840.18830.3717)
F-=(0.78550.30650.30650.08050.02280.10300.21250.29160.75050.3645
1.28650.13450.2124)
计算各方案到正负理想解的距离及贴近度,具体见表8。

表8 各评价方案的贴近度
根据贴近度计算结果可以看出,四个施工方案的优劣程度排序如下:
P1>P3>P4>P2
由此排序可知,施工方案P1的“绿色度”最高。
(5) 结果验证。为验证三标度AHP-TOPSIS模型评判结果的可靠性,本文采用模糊综合评判模型进行验证[18-19],评语集V={Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ
Ⅵ Ⅶ Ⅷ Ⅸ},Ⅰ—Ⅸ代表该指标完成情况从优到劣顺序。各评价指标权重前面已求,根据前面专家打分情况建立隶属度矩阵Z,进行多级模糊综合评判。具体如下(以方案P1为例):
① 一级模糊综合评判
E1=w1·z1=(0 0.0207 0.6134 0.1585 0.1866 0.0207 0 0 0)
E2=w2·z2=(0 0 0 0.1203 0.7940 0.0856 0 0 0)
E3=w3·z3=(0 0.4565 0.2082 0.0394 0.2663 0.0296 0 0 0)
E4=w4·z4=(0 0 0 0 0.9000 0.1000 0 0 0)
② 二级模糊综合评判
E=W·Z=(0 0.2377 0.2871 0.0842 0.3522 0.0387 0 0 0)
③ 结果处理
将评语集Ⅰ—Ⅸ分别赋予9、8、7、6、5、4、3、2、1分,评判结果量值为:
m1=6.3323
通过量值结果可以看出,方案P1各指标完成的综合水平处于Ⅲ级~Ⅳ级之间。
采用同样方法计算m2=4.8972、m3=6.3154、m4=4.9563,各量值大小关系为m1>m3>m4>m2。即四个方案的优劣排序为P1>P3>P4>P2,同样可以得出施工方案P1“绿色度”最高的结论,与三标度AHP-TOPSIS模型的评判结果相吻合。
4 结 语
为解决施工方案“绿色度”比选问题,基于三标度AHP构建TOPSIS评判模型。介绍三标度AHP基本操作流程,阐明了该权重求解方法的优势。参考相关规范、文献建立施工方案“绿色度”综合评价指标体系,基于三标度AHP-TOPSIS评判模型对某大型基坑工程进行实证研究,得出拟定的四个施工方案的优劣排序为P1>P3>P4>P2的结论,即P1为最优施工方案,“绿色度”最高。为保证三标度AHP-TOPSIS模型评价结果的准确性,采用模糊综合评判法进行验证,验证结果与三标度AHP-TOPSIS模型的评价结果相吻合。三标度AHP-TOPSIS评判模型操作相对简单、评价结果可靠,能够作为施工方案“绿色度”比选过程中的一种有效手段。

