明满流过渡的数值模拟及工程应用
梁娜娜,金 生
(大连理工大学 建设工程学部, 辽宁 大连 116024)
输水工程可以通过明渠和有压管道等途径进行输水,而在此过程中,当输水管道遇到集中输水或短时间暴雨时,管道内流量激增、水位升高,甚至充满全部管段;管路由非满管流转变为满管流,此时,管路处于完全充满的有压状态;而后随着输水量的减弱,管路内流量减小,水头逐渐下降,再次处于无压非满管流状态。这样从无压明流到有压满流,再由有压满流到无压明流的不断变换,称之为明满过渡流[1],是输水工程经常出现的水力现象。输水时发生明满流过渡,会导致管道内突然发生明显的压力变化,对管道的安全运行[2-3]造成影响,严重时可能会管道爆裂,有很大的安全隐患[4]。
明满过渡流的水力现象常出现在水电站的压力引水隧洞和压力钢管、水库的有压泄洪隧洞、居民生活用水管道等。明满过渡流是工程运行中不可避免的不利于工程的水力现象,因此,对于明满流的研究至关重要,也为长距离输水系统的安全运行提供必要的依据。1932年Meryer等[5]研究了水电站尾水隧道中的特殊流动涌浪,这是国内外对明满流最早的研究。随着水力学的不断发展,发现明满流研究的难题主要是如何处理交界面。假想窄缝法在1961年由Preissmann提出成为解决这个难题的思路,其基本理论是假设在管顶有一条极其窄的不增加管道面积和水力半径的缝隙,在水深高于管的顶部之后,湿周和过水断面面积均为恒定的。明满流水力过渡过程可以根据窄缝法的假设,采用统一的方程来求解。1999年李辉等[6]利用Preissmann窄缝法及统一的特征隐式格式,对有压满流和无压明流的方程进行了描述和求解,成功的应用于电站的动态仿真数值计算和尾水洞洞顶优化设计中。证明这个方法很好的解决了界面的问题。
1 数学模型
明满过渡流是一种在隧洞、管道中既可能出现明流,也可能出现满流的特殊的流动,即在动态过程中,隧洞、管道等某些位置的明流流动和满流流动会交替产生。在计算明满过渡流的时候,明流过渡到满流的分界面无法预先知道,管流和明渠流也就不可能明确区分并用相应的方程进行计算。因此在研究明满过渡流的问题上需要同时计算明渠流和管流,它们反映了明满流过渡过程的基本原理,是研究此类问题的理论基础。
法国科学家圣维南在1871年创立了明渠非恒定流基本方程,该方程表示的是水力要素与时间t及流程x之间的非线性关系,故又称为圣维南方程组[7]。

(1)
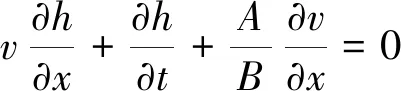
(2)
有压管道非恒定流:

(3)

(4)
式中:A表示过水断面面积;B指水面宽,沿x轴方向的流速为v;h表示水深;J是摩阻水头损失;H表示管流水头;a表示管流的水击波速;θ为管道轴线与水平线之间的夹角。
对有压管流进行等效处理是解决上述问题的思路,即加上一条竖直向上的窄缝在原计算断面的顶部,并设窄缝的宽度B=gA/c2。其中,A为断面总面积,c为管道处于满流状态的波速。因此可以用相同的方程来表示有压管道和明渠两种非恒定流。
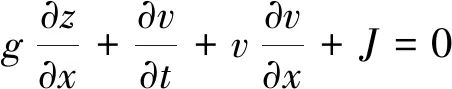
(5)

(6)
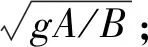
水力过渡流的控制方程是一种拟线性双曲型偏微分方程[8],精确的解析解无法直接计算得出,对于偏微分方程的定解问题,近似的数值解一般采用差分方法求得。有两种常用的方法被用来求解拟线性双曲型偏微分方程组的数值解:一种是特征线法[7,9],它将非恒定流的两个控制方程通过特征线理论转换为常微分方程组,然后沿正负特征线积分离散方程组,从而对方程中的未知变量进行求解,属于显式的解法;另一种是隐式差分法[10-11]。在数值模拟流体领域里,应用最广泛的隐式差分格式是Preissmann四点隐格式[12]。文中将采用隐式差分法进行数值模拟。离散格式为:
(7)
(8)
(9)
将式(7)、式(8)、式(9)代入控制方程中化简得:
a2jΔyi+b2jΔvi+c2jΔyi+1+d2jΔvi+1=D2j
(10)
e2j+1Δyi+a2j+1Δvi+b2j+1Δyi+1+c2j+1Δvi+1=D2j+1
(11)
从时间和空间上对控制方程进行差分,计算结果达到二阶精度。
2 模型验证
HydroInfo[13]水力信息系统可应用于流域系统的洪水、溃堤与淹没、泥沙与河道演变分析、潮流与波浪数值模拟等流动与输运问题。该系统由计算分析、信息查询、可视化演示等模块构成。计算模块将库群、河网、泄水建筑物、堤坝、蓄滞洪区与淹没区等作为大系统统一处理,根据实际问题的特点及空间分辨率要求,可以采用分区动态耦合算法分别将水量平衡关系、一维、二维与三维流动微分方程组作为控制方程。文中利用HydroInfo软件验证如下实验。
图1描述的是一条顶端封闭、断面为矩形的渠道,相关的几何参数及物理参数为:断面宽度W=0.51 m、高度h=0.148 m、长度L=10 m、底坡坡度S0=0、曼宁系数n=0.012、初始流量Q=0 m3/s 、初始测压管水头为0.128 m,上下游分别设置水位初始条件(本算例基本资料源自Wiggert[14]于1972年进行的实验)。上、下游边界条件见图2。

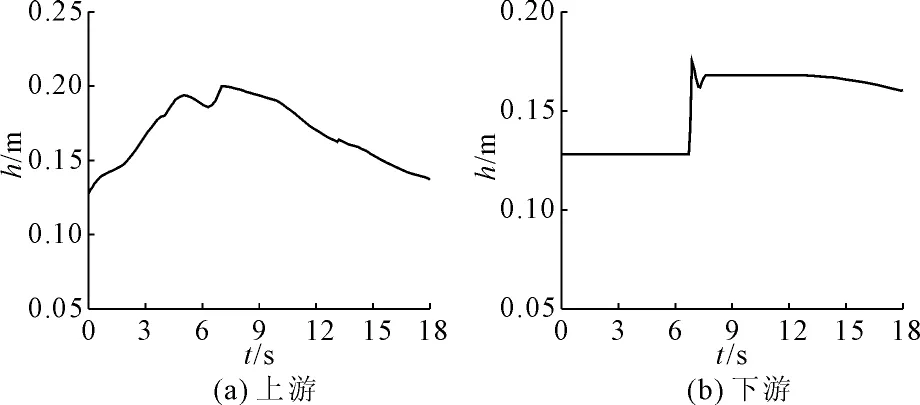
图1 Wiggert实验相关参数图(单位:m)
图2上下游水位边界条件
图3对比了不同位置的水位情况,由图3数值模拟结果与实验结果来看拟合较好,渠道各断面的水位变化范围与实验结果一致,验证了此模型的准确性,可以很好的应用到明满流过渡的计算中。
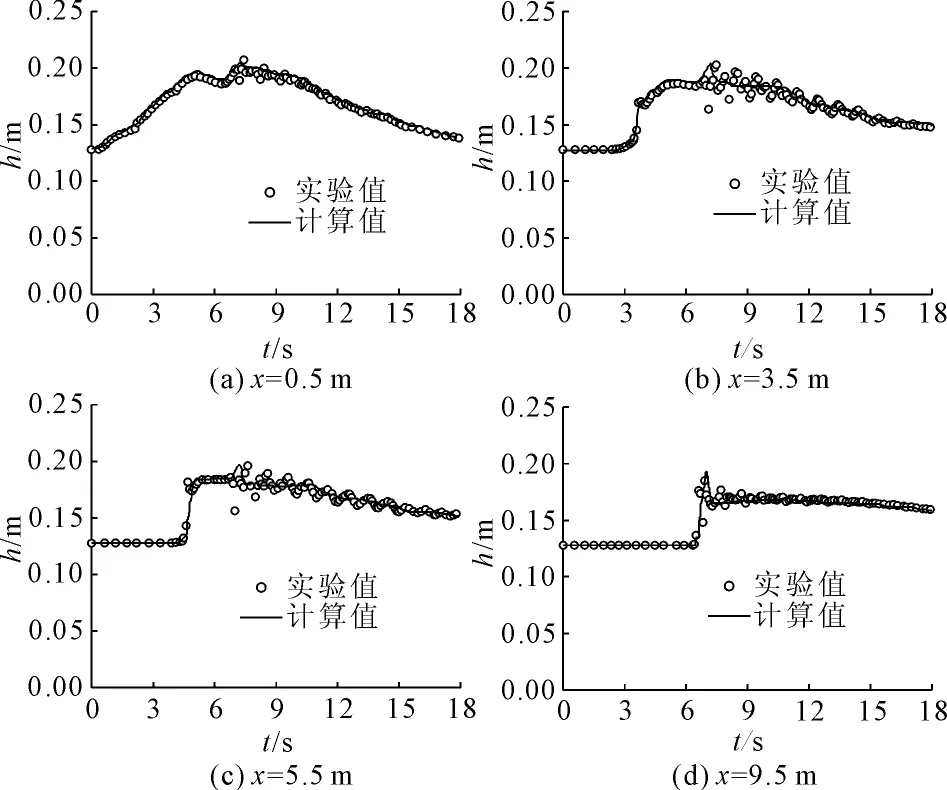
图3数值模拟结果对比图
3 工程应用
密云水库调蓄工程是团城湖至密云水库的输水工程,这是一条长约103 km,总扬程132.85 m的输水线路。向密云水库调水的调度可分为三段:即团城湖至怀柔水库段渠道调水、怀柔水库至北台上倒虹吸(雁栖泵站)段渠道调水和雁栖泵站至密云水库段PCCP管道调水。向密云水库调水时,之间的九级泵站需要被开启,如果其中的任一级泵站出现事故,势必会导致其前水位雍高,其后水位降低,影响工程正常运行,因此模拟调水工况是必要的。利用HydroInfo水利信息系统软件建立了团城湖至密云水库的渠道和管道相结合的一维水动力模型后,并添加水工建筑物如怀柔水库等,初始条件为各网段流量和水头,边界条件为水位过程、水位与流量关系。通过模拟泵站加压输水工况来分析明满过渡流在实际工程中的影响。
加压工况(自下而上):团城湖至怀柔水库段调水的水量由初始0 m3/s逐渐过渡到13 m3/s。团城湖至怀柔水库段的六级泵站采用阶梯启泵,即屯佃~西台上六级泵站每隔10 min逐级启动第1台泵,流量为6.67 m3/s,待西台上泵站启动后,再每隔10 min逐级启动第2台泵,使流量达到13 m3/s。怀柔水库至密云水库的3级泵站可适时逐级启动,由初始0 m3/s逐渐过渡到5 m3/s,怀柔水库以及密云水库闸门开度保持不变。设置边界条件:团城湖的水位过程为恒定值49 m;各网段初始流量为0,渠道各网段初始水位为底高程,管道各网段初始水头为管道轴线。
3.1 水位
图4为模拟自下而上调水工况时沿程明渠各个位置的稳态水位图,图5为从屯佃泵站到李史山泵站的泵前各网段水位随着时间的变化曲线图。由图中可知各级泵站泵前水位在何时达到稳态,何时水位开始变化,如屯佃泵前网段在1.2 h后开始有流量,水位开始变化,在4.6 h后,水位达到稳态。在实际调水中,为了保证机组的正常运行,任意两级泵站之间的渠道水位需同时满足后级泵站进口最低启泵水位和前级泵站出口淹没出流水位。根据模拟计算得到的结果,可以应用到实际调水工程中,如在何时开启关闭下一级泵站,何时达到要求水位等。


图4 团城湖—怀柔水库段稳态时水位
图5各级泵前断面水位变化曲线
从雁栖泵站开始是管道输水,最终达到的稳态水头如图6所示;图7为不同时刻管道中的水头图。从图7可以发现,t=0.1 h时,管道中的水流很小,管道未充满水,此时管道处于明流状态,t=1 h时,部分管道充满水,开始出现明满流过渡的水力现象,随着时间的推进,流量越来越大,在此输水过程中从无压管流变成有压管流,管道从下至上依次变为有压流。从计算结果中可以得知在运行16 h后全部变为有压管流,然后经过一段时间有压管道的过渡输水水头趋于稳态,管道处于恒定流状态。


图6 怀柔水库—密云水库段稳态水位
图7管道沿程不同时刻水头
3.2 流量
图8为输水过程中沿程各点不同时刻的流量图。由图8可以直观的看出明渠段面的流量,各级明渠何时开始有流量,根据最终稳态时的流量也可以看出最终明渠各网段均达到指定的输水流量;图9为各级泵站达到指定流量图,由图9可知在t=0.1 h时,一级泵站开始有流量进入,在t=11 h时,达到指定的13 m3/s流量,同样可知其他几级泵站在各时刻的输水流量,达到流量的运行时间,最终稳态流量均符合工况要求。
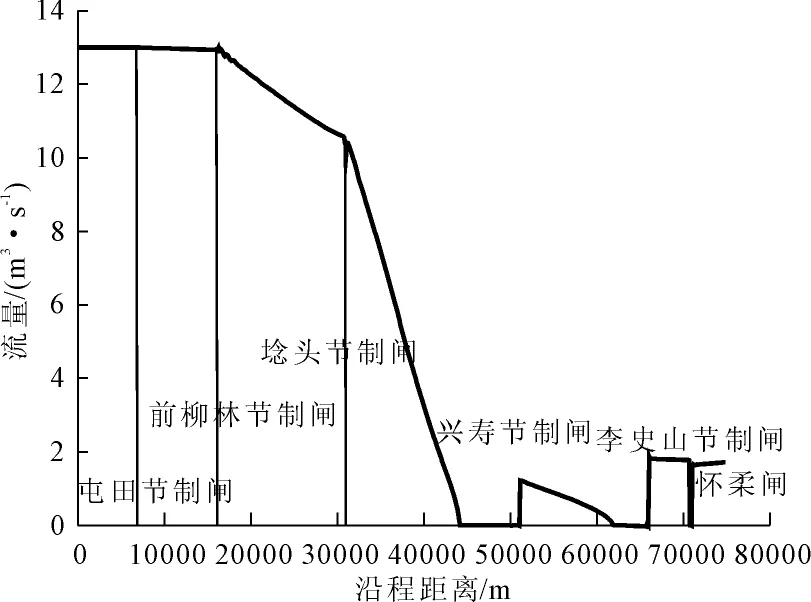

图8 明渠段某一时刻沿程流量
图9各级泵前断面流量变化曲线
图10表示某一时刻的沿程流量,由图10可以看出此时郭家坞泵站已经达到5 m3/s的流量,正在向密云方向管道输水,此时管道中前半部分已经开始有水流,流量为1.5 m3/s,在图中2 km以后无流量,根据不同时刻的沿程流量图,可以知道管道中的输水情况以及各节点的流量;图11为管道不同位置流量随时间变化图,由图11可以看出在管道入口处,流量在t=13 h时达到5 m3/s,此时管道末端刚开始有流量,通过不同位置的流量对比可以看出管道中流量不断的增大,最后全线达到稳态,流量为5.03 m3/s。在此输水过程中管道中的水流刚开始处于无压明流,随着流量不断增大,出现明满过渡流,在此过程中管道水头的变化可以作为管道设计压力的依据,对工程的设计十分必要。


图10 怀柔水库—密云水库沿程流量
图11管道不同位置流量随时间变化曲线
4 结 论
本文利用HydroInfo水利信息系统软件建立了明渠及有压管道耦合的一维水动力学模型,采用隐式差分法对模型方程在空间和时间上进行积分,得到方程的数值解,并计算相关算例与其实验值进行对比来验证该方法的正确性,最后应用到密云水库调蓄工程,并模拟调水工况,得到的计算结果表明此模型在计算明渠和管道时稳定性好,计算结果准确,在实际工程计算中具有可操作性,也为工程的安全调度提供合理建议,说明模型对调水工程有实际指导意义。

