含非贯通软弱结构面岩质边坡渐进破坏过程数值模拟

路 瑞 利

(长江工程职业技术学院, 湖北 武汉 430212)

大量的交通、矿山及水利工程建设均涉及到岩石边坡开挖与支护，其稳定性评价[1-2]是边坡工程设计重要内容之一。不同于土质边坡，岩石边坡的稳定性主要受到岩体内部发育的各类软弱结构面所控制。大多数情况下，岩石边坡开挖后并不是沿着贯通的结构面发生滑动，而是沿着非贯通软弱结构面发生扩展、连接，从而形成贯通的滑动面。因此，研究含软弱结构面岩质边坡渐进破坏过程具有重要的工程意义。

岩石边坡内部非贯通软弱结构面的扩展过程是连续介质转变为非连续介质的过程，采用常规的有限元方法无法对此进行模拟。针对此问题，唐春安等[3]基于有限元方法和材料软化理论，建立了岩石破裂过程分析(Rock Fracture Process Analysis，RFPA)方法，用以模拟岩石裂纹的萌生、扩展、汇交等过程。由于该方法仍然为连续类数值方法，因此很难模拟岩体从开裂到破碎的过程。焦玉勇等[4]、江贝等[5]、杨建成等[6]等则基于非连续变形方法(DDA)，通过在块体单元中预设虚拟裂缝单元来模拟岩石的裂纹扩展过程，虚拟裂缝单元受力发生破坏后变为真实的裂缝。由于该方法基于离散介质假设，无法模拟岩石介质从完全连续到离散的变化过程，且裂纹扩展的路径只发生在单元边界上，无法实现块体内部的破裂。严成增等[7]为了解决类似问题，基于FDEM方法，提出了基于局部单元动态劈裂的FDEM自适应方法，以克服裂纹扩展过中的网格依赖问题。该方法无需划分较密的初始计算网格，而是随着裂纹尖端扩展方向进行单元劈裂加密，但同时也增加了计算工作量。Belystco等[8-11]提出了扩展有限元方法(XEEM)，通过引入阶跃函数表征裂缝两边的不连续变形场，引入富集函数表征裂纹尖端来实现裂纹的扩展和单元的破裂。但此方法计算原理复杂，且多用于模拟单条裂纹的扩展过程，无法正确模拟含多条裂纹以及裂纹相互交叉的情况。因此，需要选择更为合适的数值模拟方法来研究岩体的裂纹扩展过程。

本文采用数值流形方法对含非贯通软弱结构面岩石边坡的渐进破坏过程进行模拟。数值流形法[12](Numerical Manifold Method，NMM)是由石根华提出的用于统一解决连续-非连续介质问题的一种新的数值分析方法,多名学者已将数值流形方法应用于不同研究领域[13-17]。与扩展有限元不同的是，数值流形方法无需引入阶跃函数表达单元内部的裂缝，而是通过不连续面切割数学覆盖后所生成的相互分离物理覆盖来形成流形单元，因此裂缝两侧为相互独立的流形单元。可见数值流形方法非常适合用于模拟岩体的裂纹扩展过程。然而原有数值流形方法建立之初主要用于贯通裂隙的不连续变形计算，而没有考虑裂隙扩展演化过程。为了将其拓展到非贯通裂隙扩展过程的模拟，本文将定义相应的裂缝起裂及扩展准则。首先通过引入带抗拉强度的Mohr-Coloumb准则用于判断岩体因剪切破坏而发生的起裂与扩展，然后引入粘结裂纹扩展计算模型来模拟裂纹尖端的裂纹过程区(Fracture Process Zone, FPZ)。最后，本文将采用数值流形方法对西南地区某水电站高边坡的渐进破坏过程进行了数值模拟，揭示高陡岩质边坡的变形及破坏机理，为岩石工程边坡的稳定性评估提供依据。

1 数值流形方法基本原理

1.1 流形单元的形成

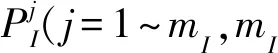
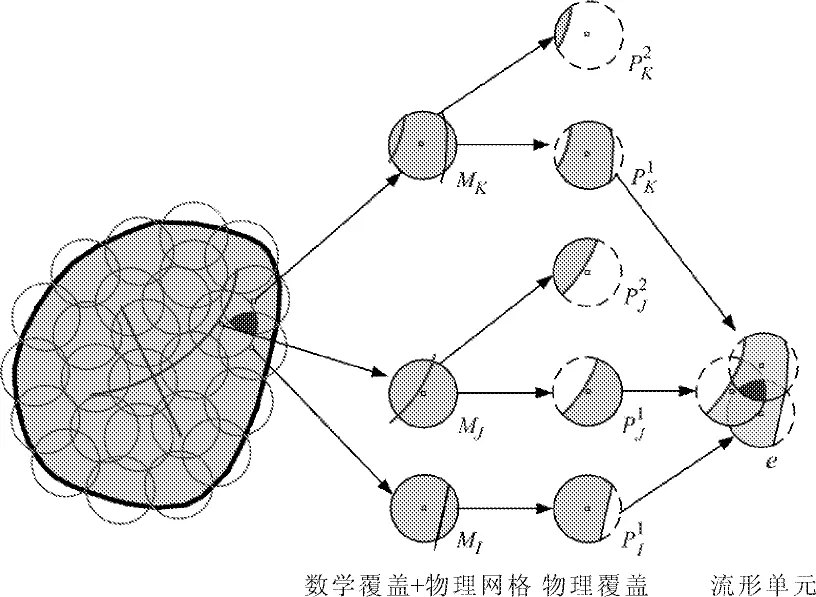
图1流形单元的形成

在每个数学覆盖上定义权重函数φI(x)，需要满足

0≤φI(x)≤1， ∀x∈MI

(1)

φI(x)=0， ∀x∉MI

(2)

包含x点的所有数学覆盖上的权函数必须满足单位划分，即

(3)

φi(x)

(4)

根据流形元的定义，位移定义了流形元E上的逼近

(5)

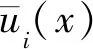
(6)

其中PT(x)是多项式基和di是矩阵中未知的向量。

一般而言，常使用三角形网格构造数学覆盖，即通过三个物理覆盖共享流形元。对于这种流形元构造方案，每一个物理覆盖假设多项式基的矩阵只有常数项，权函数φI(x)则取为常规三角形单元的权函数。

1.2 数值流形方法的计算方程

数值流形方法根据虚功原理建立计算方程，即

(7)

式中，uh为位移场近似函数及其虚位移δuh，根据式(6)，可表示为

(8)

(9)

将式(8)和式(9)带入到式(7)中，同时考虑虚位移的任意性，可得到空间上的半离散方程

(10)

其中

(11)

(12)

(13)

(14)

(15)

式中

(16)

式(10)只是空间上的半离散方程. 数值流形方法采用隐式时间积分方案进行求解,并采用Newmarkβ方法对时间域进行离散，及

(17)

(18)

以及

(19)

(20)

将式(17)、式(18)代入到式(10)中，得到数值流形方法在每一时步中的计算方程，即

KΔd=F

(21)

其中

(22)

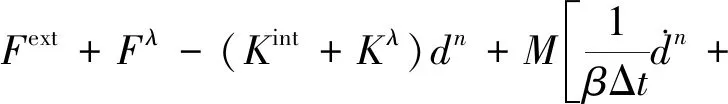
(23)

2 基于带抗拉强度Mohr-Coulomb准则的起裂算法

数值流形方法提出之初主要用于求解不连续变形问题，未考虑非贯通裂隙扩展过程的模拟。为了在数值流形方法中实现裂隙扩展计算，需要定义裂纹尖端扩展准则以及完整岩体材料的起裂准则。

2.1 带抗拉强度Mohr-Coulomb准则

选择带抗拉强度Mohr-Coulomb准则作为完整岩石起裂的准则[16-17]。在目前岩石力学中的各种准则中，该准则提出时间较早，应用范围广泛，且只包含了三个计算参数，即摩擦角，黏聚力及抗拉强度。这些计算参数可通过室内试验直接获得，比如单轴压缩试验以及间接抗拉强度等。图2(a)和图2(b)分别为Mohr-Coulomb准则在σn-τ空间和σ3-σ1空间的示意图。其中σn和τ分别为法向应力和剪切应力，和分别为最大和最小主应力。图2(b)中斜线为剪切强度包络线，表示为：

(24)

式中：c为黏聚力；φ为内摩擦角。

根据Mohr-Coloumb准则，与主应力呈β角的斜截面上，剪应力最先达到剪切强度，该平面即为破裂面，并有：

(25)

最大主应力σ1和最小主应力σ3之间的线性关系如图2所示。其中，包络线的斜率表示为：

(26)

图中包络线与第一主应力轴的截距为岩石的单轴抗压强度σc，表示为：

(27)

如果图2(b)中的包络线向σ3的负方向延伸，当σ1=0时，包络线与横坐标轴的截距为材料的单轴抗拉强度的表观值，表示为σT：

(28)

事实上，岩石力学实验所测得的岩石抗拉强度远小于式(5)所给出的岩石表观抗拉强度值。因此，应在Mohr-Coloumb准则中考虑实测抗拉强度T0，如图2所示的竖直线。

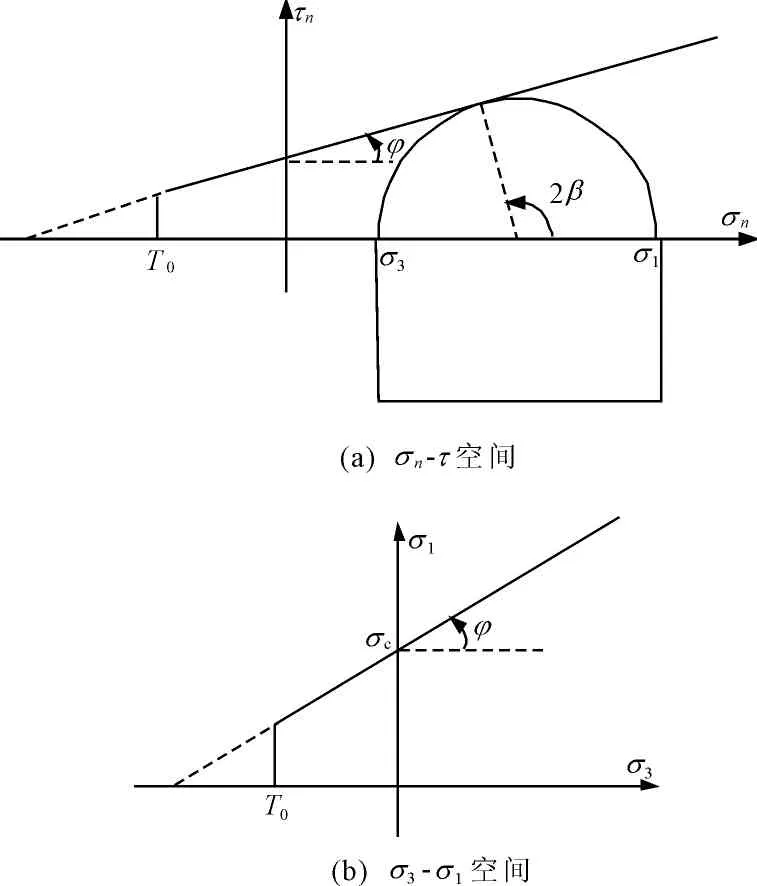
图2带抗拉强度的Mohr-Coloumb准则

2.2 裂纹生成算法

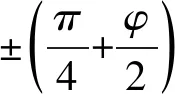
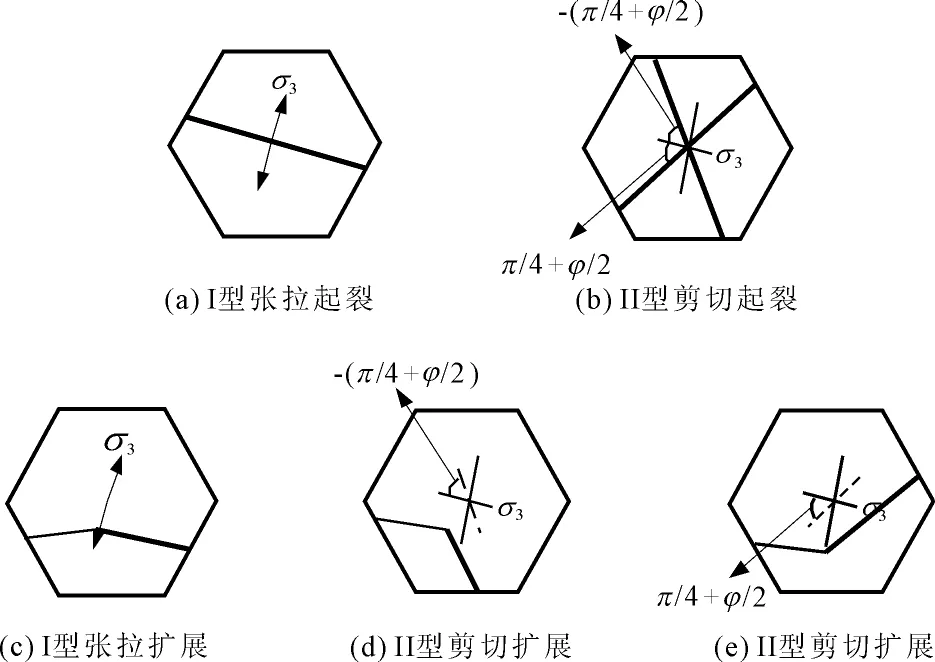
图3裂纹起裂及扩展算法

(细线为已有裂纹，粗线为新生成裂纹)

在实际计算过程中，将新生成的流形单元的应力重置为0。同时，这些单元周围应力场也将重新分布并达到新的平衡。事实上这种处理方式是可行的，因为无论将新产生的流形单元的应力置为零或是继承发生裂隙扩展前的流形单元应力，均近似地满足当前应力场。经典的线弹性断裂力学理论分析表明在裂纹扩展过程中，单元内部的部分应变能释放后转变为形成新裂纹所需要的表面能。

3 边坡变形破坏过程模拟

3.1 地质条件

图4是西南地区某水电站大坝附近的开挖边坡，该边坡为反倾坡，岩层倾角为70°～85°，岩性为板岩、变质粉砂岩。发育的断层包括沿着边坡岩体的岩层方向的f9、f11、f12等、顺坡向断层f42以及规模较大的断层f1。以上主要发育的软弱结构面控制着边坡的整体稳定性。其中断层f42和断层f1为2条中倾坡外的软弱结构面，构成底滑面，对边坡稳定不利，陡倾坡内断层(f9、f11、f12等)则构成潜在不稳定块体的后缘及下游侧边界。

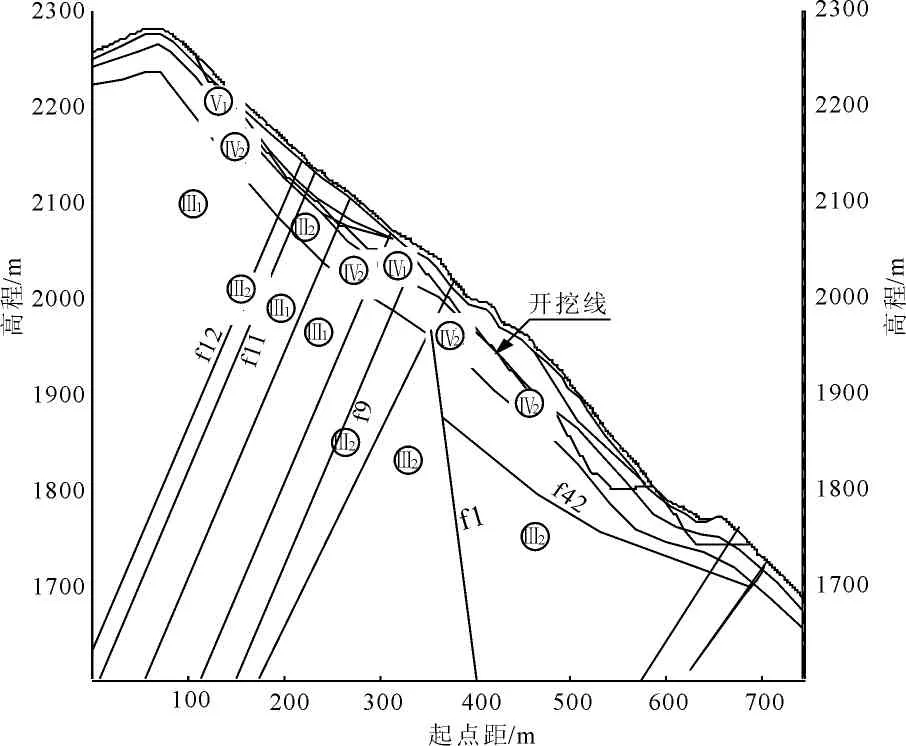
图4边坡典型剖面图

3.2 模型概化、计算网格及计算参数

依据该边坡可能的破坏，结合实际工程地质条件，本文在开展数值模拟时忽略覆盖层、风化界线以及岩体等级线边坡稳定性的影响，仅考虑控制性顺层方向的断层f42、和后缘非贯通断层f1等，并只考虑2 050 m平台以下的边坡。图5给出了概化后的地质模型及其数值流形方法的计算网格，其中数学覆盖数为760，物理覆盖数为815，流形单元数为1 508。岩体的力学参数为：弹性模量E=8 GPa，泊松比μ=0.23，内摩擦角φ=35°，黏聚力c=4.8 MPa，断裂能Gf=145 N/m，抗拉强度T0=1.0 MPa。在计算过程中考虑了软弱结构面的接触状态，软弱结构面的计算参数取值为：内摩擦角φ=20°，黏聚力c=10 kPa。

3.3 计算分析及讨论

边坡开挖完成后，基于上节根据地质建议给出的边坡计算参数，边坡仅在自重作用下是稳定的，无法形成贯通滑动面。本文借鉴边坡稳定分析中常用的强度折减法对软弱结构面参数进行逐步折减，以得到最可能出现的滑动面组合形式。当软弱结构面计算参数降低至给定参数的0.78倍时，边坡开始失稳破坏，得到的滑坡形成过程如图6所示。

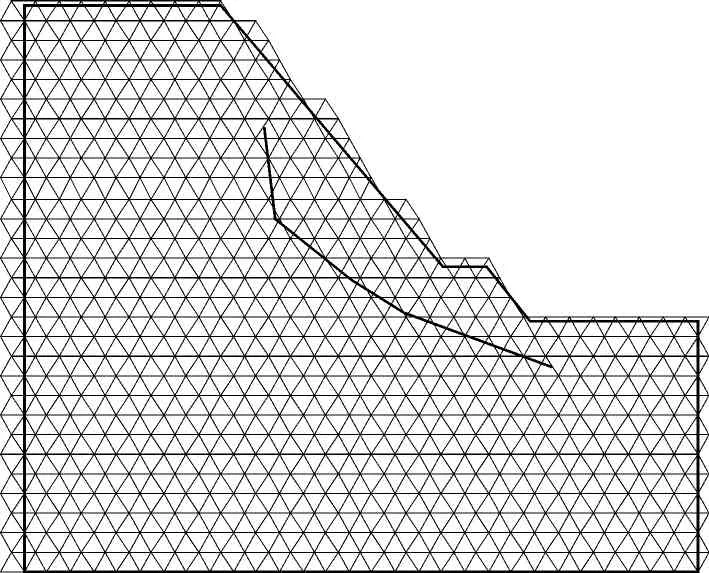
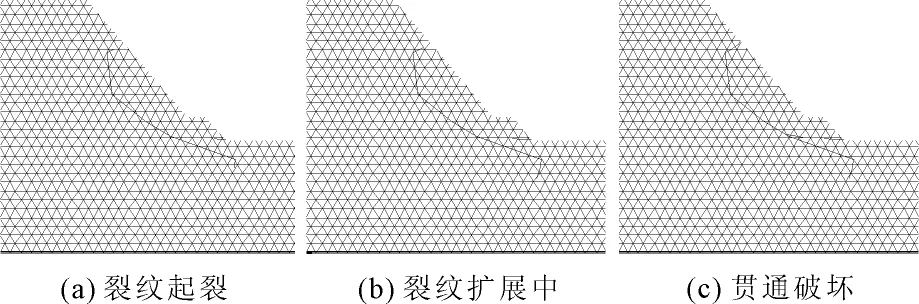
图5 计算模型概化及数值流形方法网格图

图6边坡裂缝扩展过程图

图7给出了裂纹扩展前边坡主应力分布图。由图7可知，断层f42底部尖端、后缘面断层f1有拉应力集中现象，因而发生拉伸裂纹扩展。对于断层f42，由于其底部裂缝尖端岩体水平应力较高，张拉型裂缝扩展一个弯折段后即没有进一步扩展。而后缘断层f1上部的张拉裂缝则逐渐扩展至边坡表面。由于边坡坡脚处压应力集中，因此该部位也会形成初始剪切裂缝，并逐渐向边坡内部扩展，最后止于断层f42。这样由坡脚的剪断岩体裂缝、断层f42、断层f1及其剪断拉裂缝形成贯通底滑面。

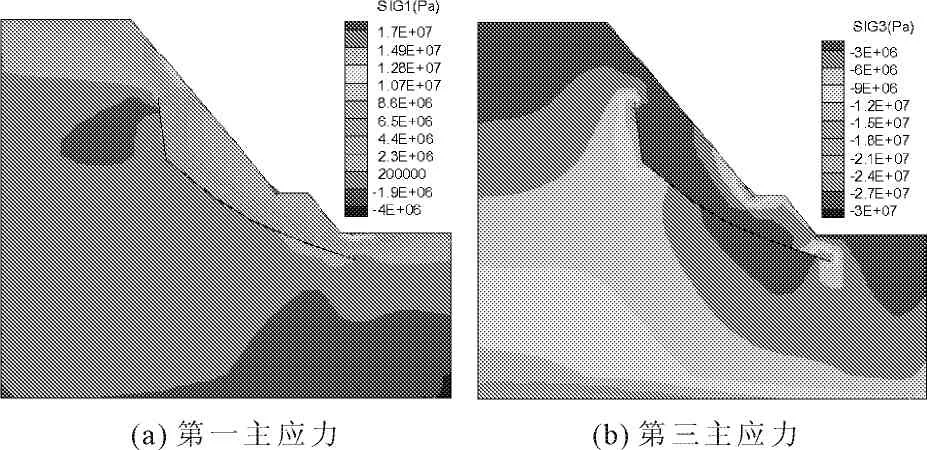
图7裂缝扩展前边坡主应力分布云图

边坡内部非贯通软弱结构面是边坡稳定的控制因素。分析上述软弱结构面扩展过程可知，坡脚处的剪切裂缝主要由于压应力集中所致，此外，坡脚附近的断层f42上盘岩体较薄，再考虑到软弱结构面抗剪强度较低，底滑面的抗滑力较小，使得f42上盘岩体受到剩余推力较大。可见，为了保证边坡稳定，在边坡开挖时应尽量避免开挖和破坏边坡坡脚处岩体，必要时采用加固措施(如锚杆、锚索等)对坡脚处进行加固。同时，也可通过工程措施提高潜在滑体的抗滑力，比如在软弱结构面上布置斜井置换洞、锚固洞、抗剪洞等。

4 结 论

含非贯通软弱结构面岩质边坡的变形破坏过程涉及岩体从连续转变为非连续状态的过程，是岩石边坡工程的研究难点之一。本文采用数值流形方法对含非贯通软弱结构面岩质边坡的变形破坏过程进行研究，得到如下结论：

(1) 基于两套覆盖系统(数学覆盖和物理覆盖)，数值流形方法可方便地描述岩体非连续变形场，非常适合模拟岩体的连续-非连续变形。通过在裂隙尖端引入黏聚裂纹模型，同时引入岩体起裂与扩展的Mohr-Coloumb判断准则，在数值流形方法中实现了模拟岩体裂隙扩展过程。

(2) 对某水电站含非贯通软弱结构面边坡的渐进破坏过程进行了模拟，计算结果表明边坡开挖后坡脚处f42断层上盘岩体由于压应力集中而引起剪切型裂缝起裂并逐渐贯通至断层f42，后缘面断层f1上部裂缝尖端则发生张拉型裂纹并贯通至坡表，最终形成完整贯通的滑裂面。

(3) 针对数值模拟揭示的边坡破坏机理，提出在施工期应尽量避免对边坡坡脚处岩体的开挖和破坏，并对坡脚进行必要的加固(如锚杆、锚索等)；通过工程措施提高潜在滑体的抗滑力，在软弱结构面上布置抗剪洞、锚固洞、斜井置换洞等。