油墨组分比例预测模型与方法

李 婵，万晓霞*，吕 伟

(1. 武汉大学 印刷与包装系，湖北 武汉 430079； 2. 深圳劲嘉集团股份有限公司，广东 深圳 518105)

1 引 言

计算机配色是纺织、印染、涂料等着色相关行业用于产品研发和质量控制的一种方法与技术[1]，它彻底改变了依赖人工经验配色为主的行业现状，降低了生产成本，是长期以来科研院校和行企关注的热点，其技术的核心是建立用于预测目标色样各基色组分比例的配色模型[2]。

在包装印刷领域，目前使用的配色模型大多以Kubelka-Munk(简称K-M)理论为依据，将色料的光学特性(吸收系数和散射系数)与组分比例用线性加和的数学关系进行描述[3-5]。有学者经实践后指出，K-M配色模型中色料的光学特性与组分比例不总成线性关系[6]；另外用加和关系描述色料在混合时的光学行为也是不准确的。以上两点致使其在实际应用中出现了无法准确预测组分比例问题[7]。事实上，加和模型虽使用广泛但从未被验证过。针对K-M配色模型“非线性”和“非加和性”问题，有学者认为引起非线性的原因是材料表面反射，因而提出了Saunderson修正[8]、Pineo修正[9]等方法试图通过修正光谱反射率值而提高K-M配色模型的线性程度。此外还提出了采用递归、拟合、正则化、非线性规划等数值处理方法优化配色模型求解过程，以上建模方法在一定程度上提高了配色预测精度，但本质上光学系数与比例仍然是线性相关的。与此同时，基于复频谱理论[10]、神经网络[11]、粒子群优化算法[12]等非线性配色模型不断被提出和研发，取得了较好的配色效果，但这类算法计算过程复杂，模型待定参数较多。

针对K-M配色模型中存在的问题，本文在K-M单常数配色理论的基础上，首先寻找与组分比例具有强线性相关特征的值替换散射系数和吸收系数构建油墨混合呈色模型的线性部分；然后引入非线性项，减小由单组分混合等因素引起的建模误差；最后采用加和方式整合线性部分和非线性部分，并给出非线性项的具体表达式以及待定参数确定方法，从而建立油墨组分比例预测模型与方法。

2 油墨组分比例预测模型

经多次试验观察，混合样本的组分比例与某些波长处的光谱反射率倒数[13]呈线性关系。据此，油墨混合呈色机理可用公式(1)所示的模型进行描述。该模型表示，油墨混合时，混合色的光谱反射率倒数与各组分基墨的光谱反射率倒数线性相关，混合色的光谱反射率倒数Pt(λ)大小由各基墨的光谱反射率倒数Pc,i(λ)大小、各基墨的组分比例ci(λ)以及非线性项ε(λ)决定。公式(1)中，m表示基墨数量，Pt(λ)和Pc,i(λ)均可用分光光度计测量得到的光谱反射率求倒得到：

(1)

根据油墨混合呈色模型，油墨配方预测实际就是已知Pt(λ)，求解ci(λ)的过程，由于ci(λ)表示各基墨的组分比例，所以它的解应具有非负性和有界性。求解ci(λ)的数学模型可表示为：

s.t.c1+c2+…+cn=1

c1,c2,…，cn≥0,

(2)

公式(2)为一个典型的约束最优化问题，利用最小二乘法可对ci(λ)进行求解。以两种基墨混合而成的混合色为例，求解该混合色组分比例ci(λ)的目标函数可写为：

minc1×Pc,1(λ)+c2×Pc,2(λ)+ε(λ)-Pt(λ)，

(3)

其中，Pc,1(λ)和Pc,2(λ)为两种基色油墨的光谱反射率倒数，Pt(λ)为混合油墨的光谱反射率倒数，c1和c2为待求的基墨1和基墨2的组分比例。另外，为了顺利求解c1和c2，令公式(3)中非线性项ε(λ)为以两种基墨的光谱反射率倒数乘积为底的幂函数，具体表达式如下：

(4)

经多次试验获知，指数n的取值范围为[0.2～2]较为合适。

综上所述，提出的油墨组分比例预测模型计算过程简洁，无复杂的迭代运算，仅选择线性程度较高的特征波段进行运算，与利用全波段光谱数据进行组分预测的算法相比，精度可大大提高。应用油墨组分比例预测模型首先需制作若干组比例已知的混和色样，在此基础上计算并选择组分比例与光谱反射率倒数线性程度较好的波段代入公式(2)进而解得目标样的组分比例，为保证计算精度，波段数不能小于基墨数量。

3 实验数据处理与分析

为了验证提出方法的有效性，本文设计了若干油墨混合方案，将UV胶印油墨中常用的四色红、四色黄和四色蓝3种基色油墨按照预定的配比混合，制成混合样本。各样本的基墨组分比例如表1所示。制样时，首先根据表1准确称量基墨，充分混合后再利用IGT适性仪在230 g/m2的白卡纸上进行打样，待样本在UV紫外灯下固化干燥后，使用分光光度计测量所有样本在400～700 nm波长范围内的光谱反射率。为减少实验误差，每个样本的光谱反射率由3次测量取平均确定。表1所示的样本中，T01、T02和T12为四色蓝与四色红油墨混合配方预测实验的建模样本，T10、T11、T13、T14为目标样本，以上样本统归为第一组实验样本；T01、T03和T17为四色蓝与四色黄油墨混合配方预测实验的建模样本，T15、T16、T18、T19为目标样本，以上样本统归为第二组实验样本。

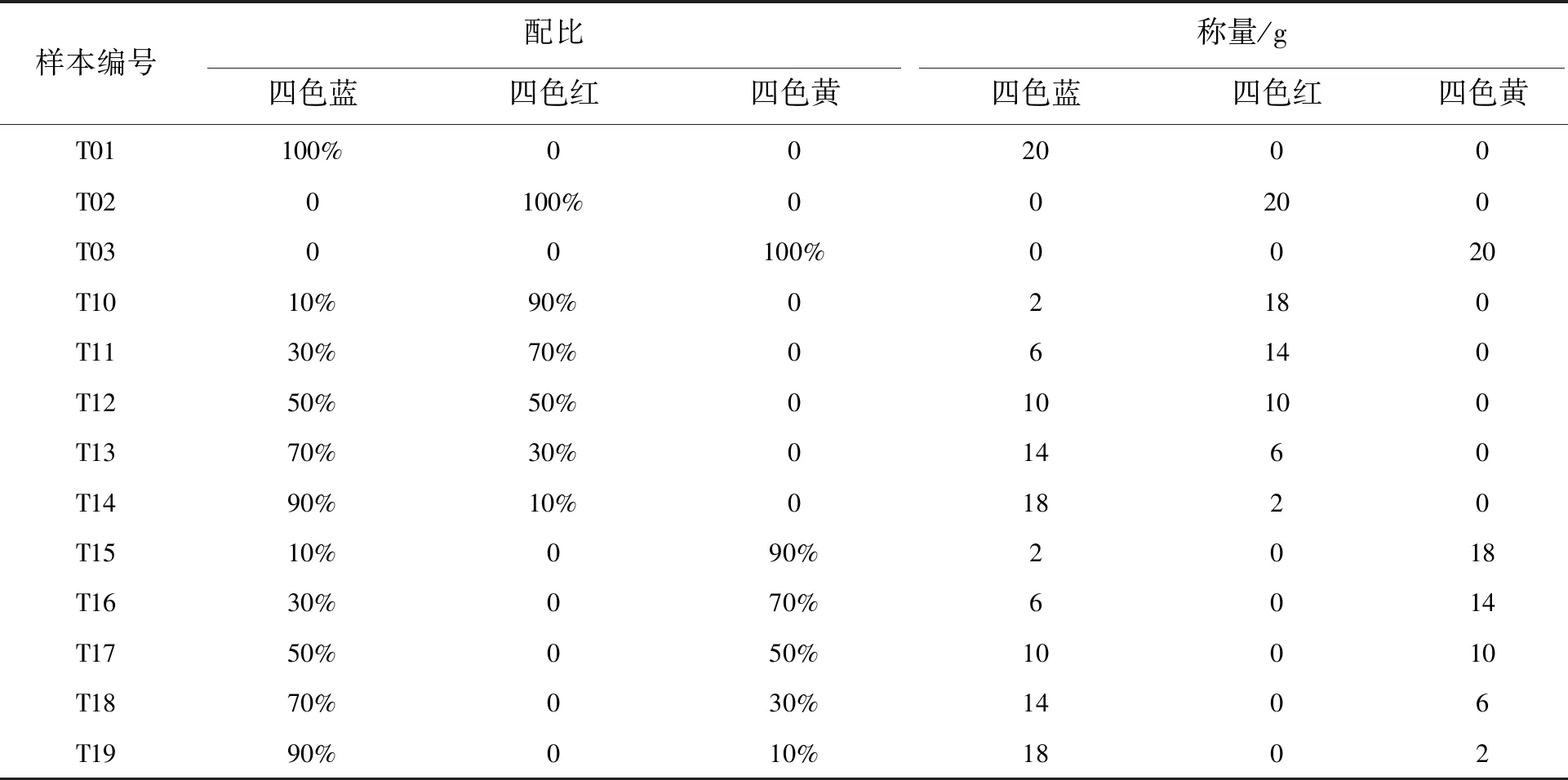
表1 样本基色油墨比例设置

3.2 油墨组分比例预测

根据第2节介绍的方法，混合油墨组分比例预测首先需确定建模样本光谱反射率倒数与已知的组分比例线性相关程度最佳的两个波段。图1(a)、(b)分别为第一组和第二组建模样本的光谱反射率倒数。由于建模样本组分比例已知，两组样本在400～700 nm波长范围内，光谱反射率倒数与组分比例线性程度最佳的波段和线性相关系数R2如表2所示，均属强线性相关，符合模型计算要求。

由公式(4)可知，确定了最佳波段后，非线性项ε(λ)的指数n仍未知。此外，实际应用中，公式(3)和(4)求得的仅是组分比例，而目标样本的组分比例未知，无法对预测结果直接进行评价，但光谱反射率值是已知的，故可以先为n赋值，代入模型求得组分比例，然后估计目标样本的光谱反射率，以光谱反射率差异最小对应的n值作为最终的非线性项指数，输出该n值对应的计算结果即为目标样本的预测组分比例。

具体估计目标样本的光谱反射率时，以3个建模样本的组分比例、光谱反射率倒数以及目标样本预测组分比例为基础数据，利用三次样条插值法估计目标样本在可见光范围内各采样波长处的光谱反射率倒数，再将计算结果求倒以获得目标样本的光谱反射率。目标样本预测光谱反射率与真实光谱反射率之间的差异可以用光谱均方根误差RMS衡量，另外考虑到光谱反射率不能直观反映人眼感知，增选色差指标ΔE与RMS共同用于确定最适合的n值。图2和图3表示两组样本在n值不同的情况下目标样本的估算光谱反射率与真实光谱反射率的差异。

表2 二组建模样本光谱反射率倒数与比例线性程度最佳的两组波段

Tab.2 Two sets of wave bands with the best degree of linearity between the reciprocal of spectral reflectance and the components proportion

第一组建模样本第二组建模样本λ/nmR2λ/nmR2500 0.999 7490 0.997 7610 0.995 0580 0.999 9

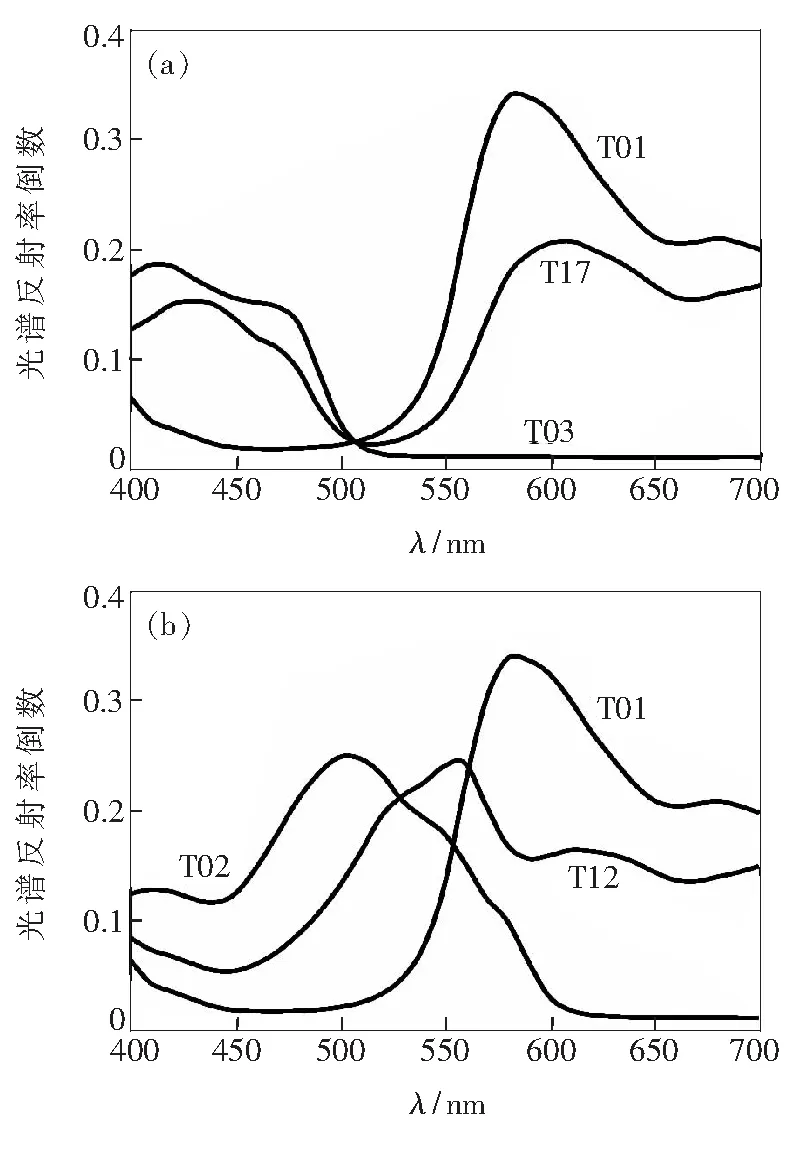
图1 二组建模样本的光谱反射率倒数

Fig.1 Reciprocal of spectral reflectance of two groups of modeling samples

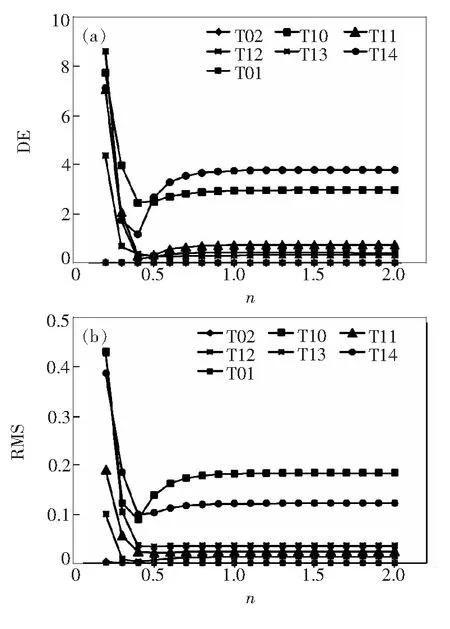
图2 n值对第一组样本色差和光谱均方根误差的影响

Fig.2 Influences ofnvalue on the chromatic difference and RMS of the first group

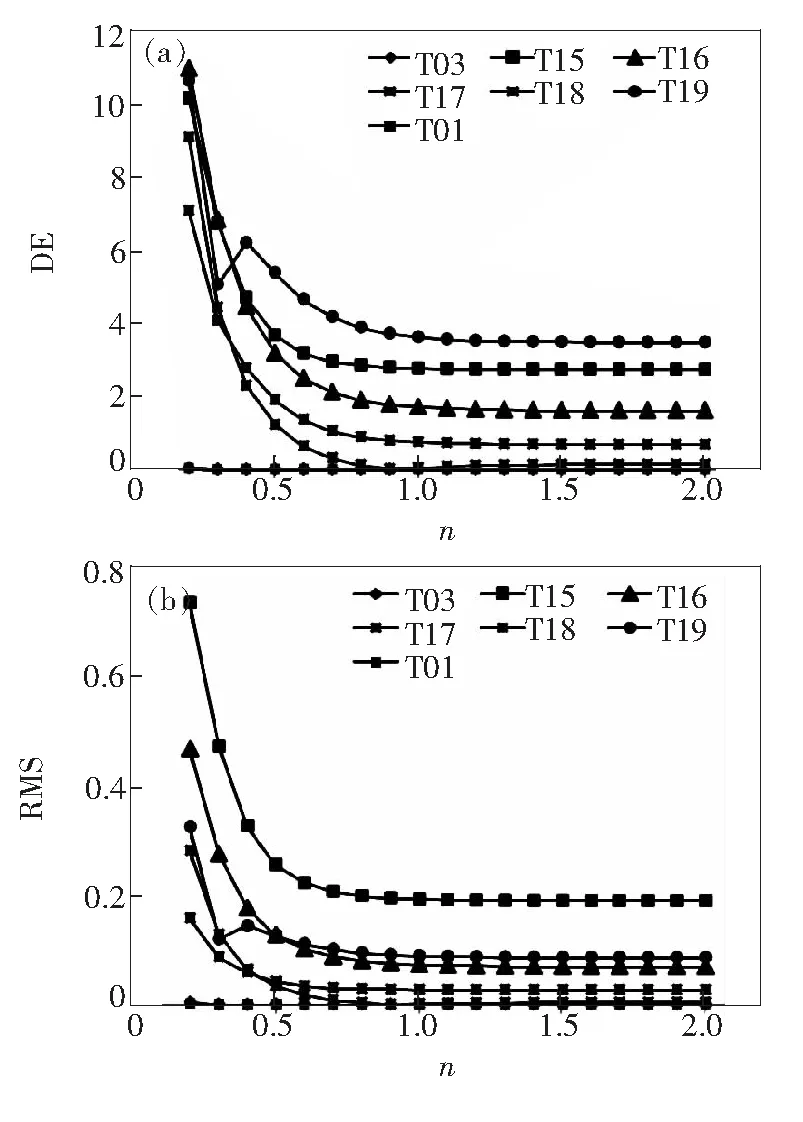
图3 n值对第二组样本色差和光谱均方根误差的影响

Fig.3 Influences ofnvalue on the chromatic difference and RMS of the second group

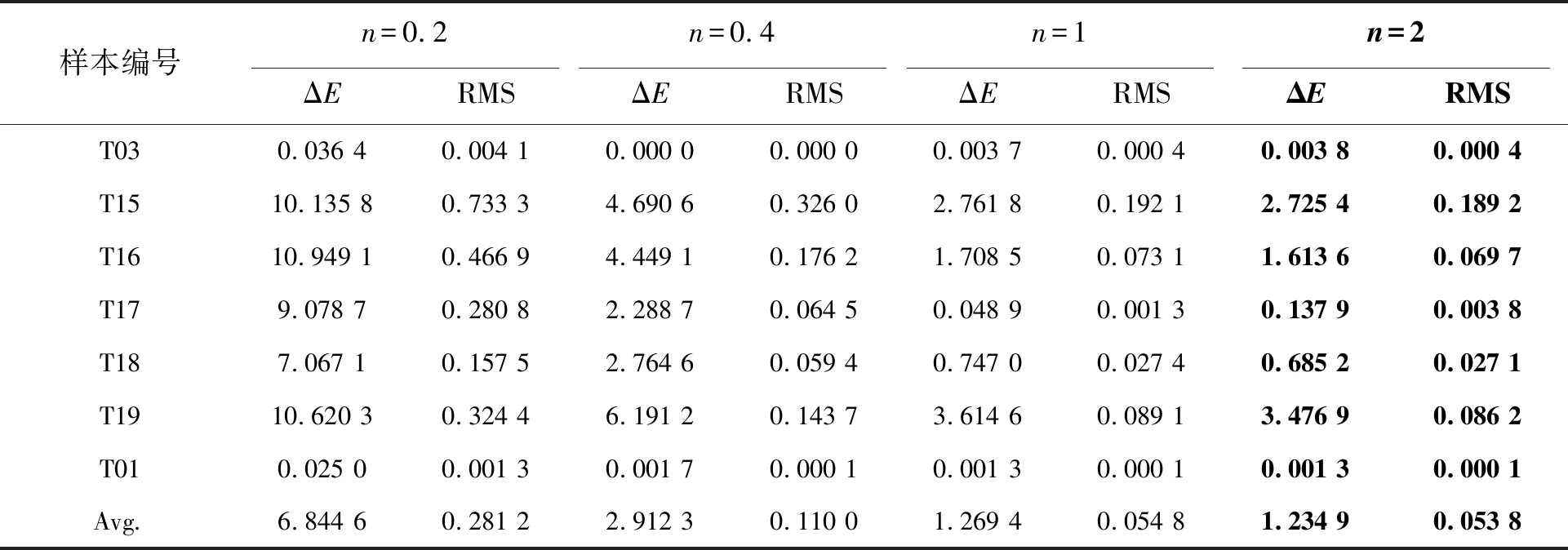
从图2和图3可以看出，n值取0.4是第一组样本色差和光谱均方根误差曲线的拐点，分别对应第一组目标样本平均色差和谱差的最小值，故第一组组分样本比例预测模型非线性项指数n值取0.4较为合适；第二组样本的色差和光谱均方根误差曲线在n大于1后，曲线均趋于平缓，此时增大n值对模型预测结果影响不大，故第二组样本组分比例预测模型非线性项指数n取大于1的值即可，本文取2。表5和表6分别对应第一组样本和第二组样本n分别取0.2、0.4、1、2时模型预测的精度评价。需要说明的是，表5和表6所示的色差和光谱均方根误差来源于组分比例预测和光谱反射率估算两个过程，它不代表真实的目标样本预测的色差和光谱均方根误差，但可用作确定最佳n值的参考。

表5和表6为n确定后，模型计算的目标样本组分比例结果。由预测结果可知，n的取值对组分比例的影响较大，从预测比例与真实比例的偏差角度分析，第一组样本n取0.4时，各样本的红基色组分比例预测结果与实际比例非常接近，平均偏差为1.57%，误差最小；第二组样本n取2时，各样本黄基色组分比例的平均偏差为3.6%，在可接受范围内。此外，表5和表6均给出了采用全波段预测组分比例的结果，由比较可知，该方法精度明显低于仅采用强线性特征波段预测组分比例的结果。其原因是：虽然两种方法的计算模型、参数估计和计算过程均相同，但全波段预测得到的是光谱反射率在所有采样波段处配色模型误差最小的解，其中大多波段与组分比例不具有严格的线性相关关系，因而产生较大误差。

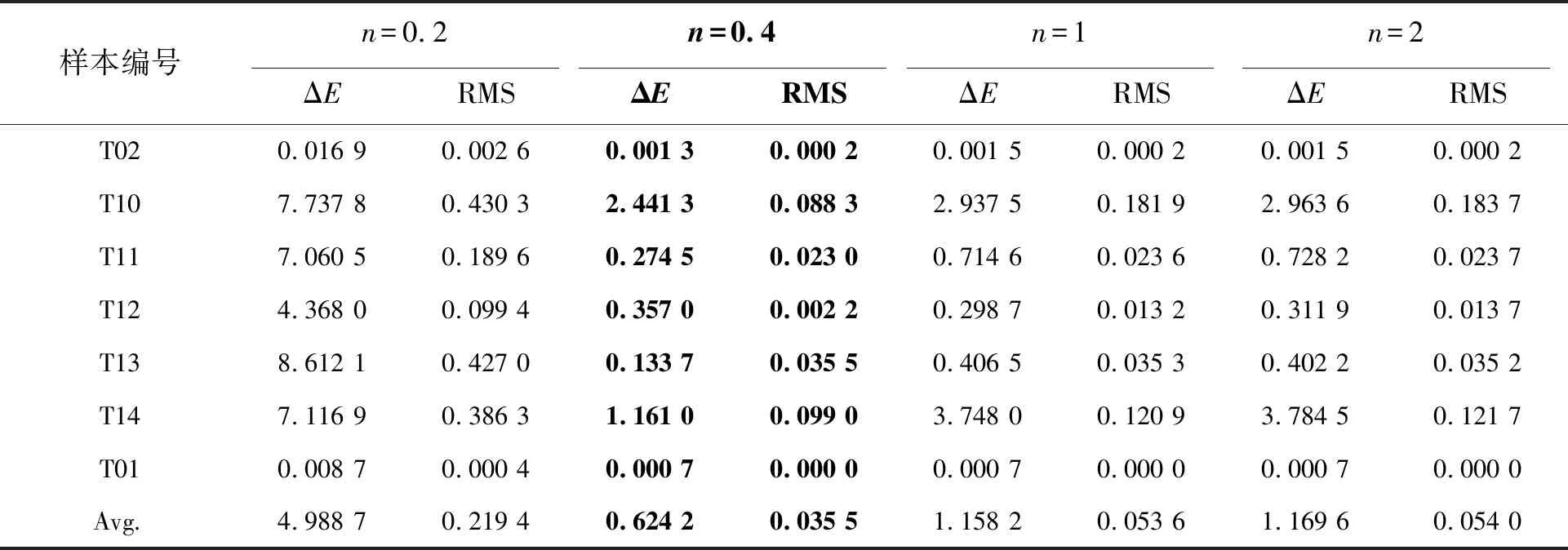
表3 第一组样本组分比例预测精度评价(色差计算条件：D65光源/2°视场)

表4 第二组样本组分比例预测精度评价(色差计算条件：D65光源/2°视场)

Tab.4 Chromatic difference assessment of ink components proportion prediction of the second group under the condition D65/2°

样本编号n=0.2n=0.4n=1n=2ΔERMSΔERMSΔERMSΔERMST030.036 4 0.004 1 0.000 0 0.000 0 0.003 7 0.000 4 0.003 8 0.000 4 T1510.135 8 0.733 3 4.690 6 0.326 0 2.761 8 0.192 1 2.725 4 0.189 2T1610.949 1 0.466 9 4.449 1 0.176 2 1.708 5 0.073 1 1.613 6 0.069 7 T179.078 7 0.280 8 2.288 7 0.064 5 0.048 9 0.001 3 0.137 9 0.003 8 T187.067 1 0.157 5 2.764 6 0.059 4 0.747 0 0.027 4 0.685 2 0.027 1 T1910.620 3 0.324 4 6.191 2 0.143 7 3.614 6 0.089 1 3.476 9 0.086 2 T010.025 0 0.001 3 0.001 7 0.000 1 0.001 3 0.000 1 0.001 3 0.000 1 Avg.6.844 6 0.281 2 2.912 3 0.110 0 1.269 4 0.054 8 1.234 9 0.053 8

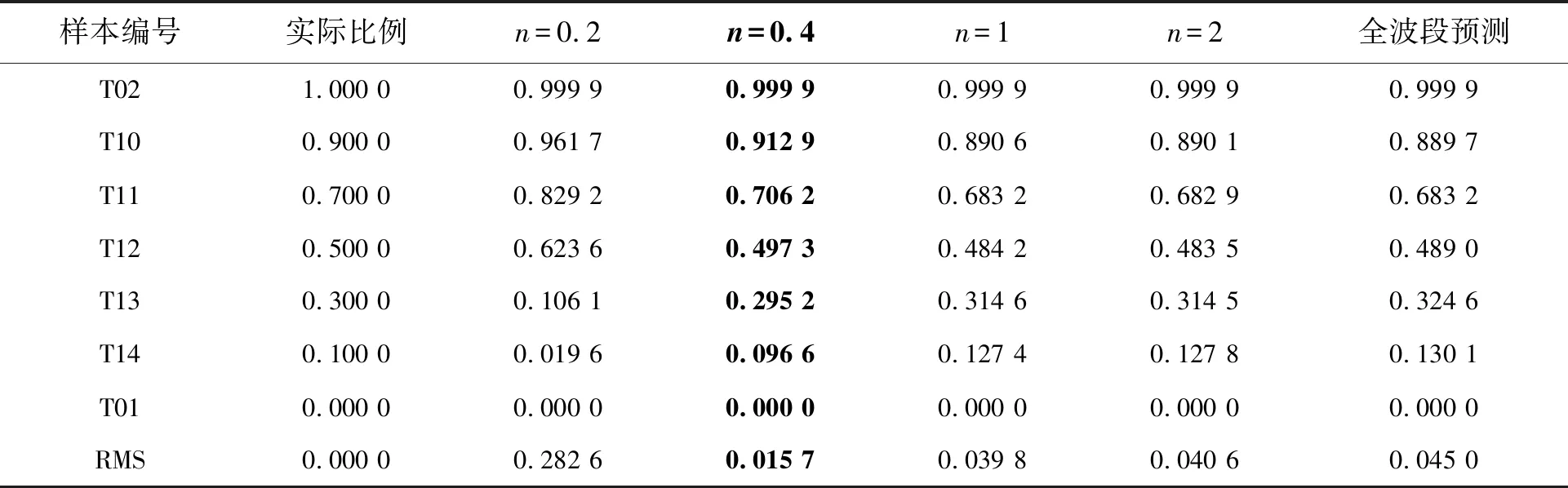
表5 第一组样本四色红基色(T02)组分比例预测结果

表6 第二组样本四色黄基色(T03)组分比例预测结果

结合表5和表3、表6和表4可知，确定非线性项指数n值方法得到的最佳n值与预测结果最优对应的n值一致，该方法简便有效，具有实用性。图4为T10、T11、T14和T13样本和其分别采用表5预测的组分比例重新打样制作的样本在标准光源箱中的对比，目视观察，4组样本色相一致，色差最大值2.06，最小值0.79，满足颜色复制要求。一般情况下，预测比例越接近真实比例，重制样本与目标样本色差越小。

图4 目标样本(左侧)与重制样本的目视比较

Fig.4 Visual comparison of four groups of target samples (left) and remade samples

利用本文提出的预测模型进行目标样组分比例预测的方法与流程可总结为图5，其中建模样本必须包含所有基色油墨样本和至少一个基色墨混合样本，基色样本用于组分比例预测计算，混合样本则用于确定线性程度最佳的特征波段和确定非线性项指数。

图5 组分比例预测方法与流程

Fig.5 Proposed method and process of ink components proportion prediction

4 结 论

基于油墨组分比例与光谱反射率倒数的关系，提出了油墨组分比例预测模型，建立了组分比例预测方法与流程，并通过实验对模型预测精度进行了研究。实验结果表明，本文提出的油墨组分比例预测模型在目标样本基墨组分已知的前提下可准确预测目标样本的比例，两组实验样本的预测平均偏差分别为1.57%和3.6%，且具有模型简洁、计算复杂度低等特点。另外该方法所需的建模样本数量少，无需制作基墨梯尺，可应对油墨批次不稳定的问题。目前该模型仅用二元混色的样本进行了验证，对三元混色目标样本的组分比例预测精度有待验证。另外，研究确定混合样本各单组分的方法以及研究各单组分在混合状态下的光学行为机制，建立更为科学的非线性项表达式也是非常有必要的。