通过变式探究 打造高效课堂*——“抛物线中一类定点问题”的教学设计

(衢州第二中学，浙江 衢州 324000)

1 设计背景

解析几何是在坐标系的基础上、用代数的方法研究几何问题的一门学科.抛物线作为一类重要的圆锥曲线，在新课程标准中摆在重要的位置.在近些年的高考中，有关抛物线的定点问题频频出现，该类问题知识综合性强，方法灵活，对运算能力和推理能力要求较高.大部分学生往往在具体问题的求解过程中因为条件多、变化活、运算繁而不知从何下手，或虽有思路却因运算不过关而“全盘皆输”.因此在复习解析几何时，要注重培养学生的数学思维能力和计算能力.

2 教学流程

本节课对课本中的一道习题(人教版《数学(选修2-1)》第73页习题2.4第6题)进行改编，然后进行一系列的变式教学，对抛物线中一类定点问题进行了一系列的深入研究.此类问题都是在围绕探求“变中的不变量”进行的.

3 课堂实录

例1已知点A,B在抛物线y2=4x上运动，O为坐标原点，且kOAkOB=-1，求证：直线AB恒过一定点(4,0).

师(PPT展示)：同学们，例1是我们昨天的作业，想必大家都已经认真研究过了，现在老师先展示大家作业中的3种主要解法(略).

变式1如果将条件kOAkOB=-1改为kOAkOB=m(其中m为常数，且m≠0)，直线AB是否仍然恒过一定点？

设计意图让学生在直观感受的基础上，由特殊到一般，将条件kOAkOB=-1弱化成kOAkOB=m(其中m为常数，且m≠0)，产生猜想，进而在教师的引导下学生小组合作验证猜想、论证结论，最后探究得出一般规律.

师：下面我们一起来思考变式1，如果我们将条件kOAkOB=-1弱化成kOAkOB=m(其中m为常数，且m≠0)，直线AB是否仍然恒过一定点呢？大家分组讨论，看看哪个小组的方法多？哪个小组的方法好？

(学生分组合作、交流探究，教师巡视，并根据各小组探究产生的困难和疑问进行适当的引导.选3名学生上台，对具有代表性的解法进行板演.)

于是直线AB的方程为

即

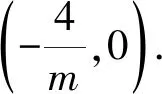
生1：老师，方法1中直线AB的方程为

师：是的，有道理.是不是解法1错了呢？

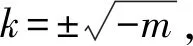
师：生1考虑问题很全面，赞一个.

从而

于是直线AB的方程为

即

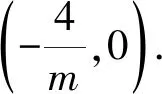
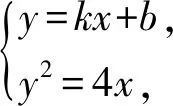
k2x2+(2kb-4)x+b2=0,

从而

因为kOAkOB=m，所以

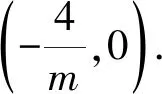
师：解法3有漏洞吗？

生2：用点斜式和斜截式设直线方程时，会漏掉斜率不存在的直线.

(教师巡视，并请生3在黑板上板演.)

y2-4ty-4b=0，

于是

y1+y2=4t,y1y2=-4b.

因为kOAkOB=m，所以

得

则直线AB的方程为

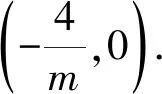
师：3种解法对比起来，哪种解法运算量小一点呢？

生(异口同声)：解法3呀!

变式2如果将条件kOAkOB=m改为kMAkMB=m(其中m为常数，且m≠0)，M(1,2)，直线AB是否仍然恒过一定点？

设计意图进一步由特殊到一般，将原点拖动到抛物线上其他一点，产生猜想，让学生独立验证猜想、论证结论，从而探究得出更一般的规律，清楚地认识问题的本质.

师：如果将原点拖动到抛物线上其他一点，如M(1,2)，其他条件不变，直线AB是否仍然恒过一定点？

y2-4ty-4b=0,

于是

y1+y2=4t,y1y2=-4b.

因为kMAkMB=m，所以

得

(做到这一步，生4不知如何是好，很着急的样子.)

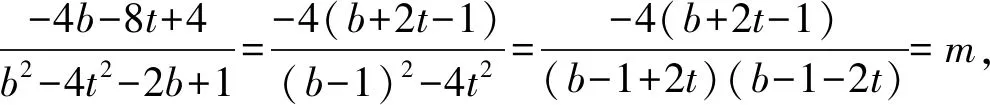
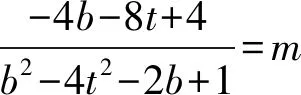
得

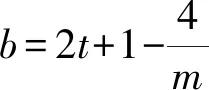
从而直线AB的方程为

(全体学生响起了热烈的掌声.)

变式3如果将点M(1,2)改为M(1,0)，是否存在实数m，当kMAkMB=m(其中m≠0)时，直线AB是否仍然恒过一定点？

设计意图在教师的引导下进行更大胆地猜想，将抛物线上的点改为不在抛物线上的点(避免运算量过大，我们选取x轴上的点)，引发学生的思考，激发他们的广泛兴趣.

(教师用几何画板展示，引导学生课后去探究验证.)

变式4如果将条件kOAkOB=-1改为kOA+kOB=-1，直线AB是否仍然恒过一定点？

设计意图促使学生在前一规律的基础上引发猜想，通过类比的思想将条件kOAkOB=-1改为kOA+kOB=1，旨在培养学生的创新意识，提高认识问题和解决问题的能力.

师：我们前面都在研究两条直线斜率的乘积为定值的形式，大家想想还有其他的形式吗？

生6：可以考虑除、加以及减的形式.

师：非常好！老师已经研究过了，加的形式有同样类似的结论，除和减没有这么漂亮的结论，课后大家可以去探究.现在我们一起来试一个加的形式，请看变式4.

y2-4ty-4b=0，

从而

y1+y2=4t,y1y2=-4b.

因为kOA+kOB=-1，所以

得b=4t，从而直线AB的方程为

x=t(y+4)，

于是直线AB恒过定点(0,-4).

师：非常好！我们把刚刚研究的kOAkOB为定值的思路改为kOA+kOB为定值的形式，请大家课后去探究上述研究成果是否仍然成立？

(教师引导学生课后去完成变式5～7.)

变式5如果将条件kOA+kOB=-1改为kOA+kOB=m(其中m≠0)，直线AB是否仍然恒过一定点？

变式6如果将条件kOA+kOB=m(其中m≠0)改为kMA+kMB=m(其中m≠0)，M(1,2)，直线AB是否仍然恒过一定点？

变式7如果将条件M(1,2)改为M(1,0)，是否存在实数m，当kMA+kMB=m时，直线AB仍然恒过一定点？

变式5～7的设计意图水到渠成，猜想并论证结论，让学生进一步深刻体会特殊到一般的思想方法.

课堂小结教师让学生谈谈这节课的收获，根据学生的反映从三维目标进行小结：我们主要学了哪些知识？体会到了哪些思想方法？最大的收获是什么？

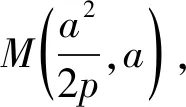
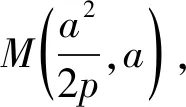
布置作业

1)上交作业：完成变式5～7及拓展1～2.

2)长期作业(小组合作，形成小论文)：①如果把抛物线上的点改为平面内任意一定点，探究直线AB是否仍然恒过一定点；②如果把刚刚研究的问题类比在椭圆和双曲线中，请探究是否仍然有上述类似的结论.

4 教学设计思路与教后效果分析

4.1 教学思路

古人云：“知之者不如好之者，好之者不如乐之者.”兴趣是最好的老师，在专题复习课上，通过变式教学，增加一些探究元素，既节约了学生审题的时间，也有利于让学生迅速产生兴趣进而积极主动地求索.变式教学活动改善了“老师讲、学生听”的被动局面，变教师的“独唱”为学生的“合唱”，充分吸引学生的主动参与，真正发挥学生的主体作用，一题多变，逐步探究，可以启迪学生的思维，发现问题的一般规律.本节课遵循新课改理念，即以学生为主体、以教师为主导，避免了就题论题，在时间有限的课堂上既突破了重点又攻克了难点，教师在变式教学过程中通过设问、猜想、加强和弱化条件等手段展开探究，充分发挥了例题的辐射作用，有效地提高了教学效率.

课堂上教师首先引导学生考虑将条件kOAkOB=-1弱化成kOAkOB=m(其中m为常数，且m≠0)，让学生探究直线AB是否仍然恒过一定点.其次考虑将原点拖动到点M(1,2)，保持kMAkMB=m(其中m为常数，且m≠0)条件不变，教师和学生一起探究直线AB是否仍然恒过一定点.研究之后,又引导学生课后去验证对抛物线上任何一点是否同样有类似的结论？然后乘胜追击提出问题，如果将抛物线上的点改为不在抛物线上，引发学生的讨论和思考.由于考虑到运算量太大，教师先找了x轴上的一点M(1,0)，提出问题：是否存在实数m，当kMAkMB=m(其中m≠0)时，直线AB仍然恒过一定点？

按照这一系列的研究思路，教师再一次提出问题“前面都是在研究两条直线的斜率乘积为定值的条件下进行的，可否将乘积形式改为其他形式呢”，再一次引发学生的思考与共鸣.有学生提出相除、相加等形式，教师顺势将条件kOAkOB=-1改为kOA+kOB=-1，让学生上台进行演板展示.然后再迁移到将条件kOA+kOB=m(其中m≠0)，甚至将kMAkMB=m(其中m≠0)改为kMA+kMB=m(其中m≠0)，让学生课后去探究直线AB是否仍然恒过一定点.整个教学过程设置了一系列的变式，引导学生以自主探究、合作交流的方式学习，一方面帮助学生学会全面的看待问题，另一方面也帮助学生培养思维的广阔性.

4.2 教后效果分析

孔子曰：吾日三省吾身.下面来说一下本次教学的得与失.

4.2.1 成功之处

1)探索——探索性自主学习的源泉.本节课设计的一大特点是学生自主探索学习，它有两个显著的特征：其一是教学内容的问题化，即以问题为中心组织教学内容；其二是教学过程的探索化，即教师创设学习环境，由学生独立地探索、发现知识和解决问题.教师留给学生充分的时间和空间进行质疑、探索、讨论与思考，在实践操作中感知、体验数学知识，经历数学知识的全过程，增加学生学习数学的自信心和成就感，努力构建有利于学生发展的有效的数学课堂.

2)变式——探索性有效教学的捷径.本节课最大的亮点是在设计过程中较好地运用了“变式训练”，提高了课堂效率.同时问题的变式难度呈阶梯化递进，使各个层次的学生都有动手的空间.这些变式本着“由简到繁、由静到动”的顺序，一步步加大题目的开放性，增加题目挖掘的深度和广度，实现学生认识的螺旋上升.

3)思想——探索性有效学习的灵魂.本节课的另一大特点是在教学过程中渗透数学思想和方法，抓住数学的本质，这是数学的灵魂.布鲁纳曾指出：领会基本数学思想和方法是通往迁移大道的“光明之路”.在基本数学思想和方法的指导下驾驭数学知识，就能培养学生的概括能力和思维能力，使数学学习变得容易.因此数学教学不能满足于单纯的知识灌输，而是要使学生掌握最本质的东西，用数学思想和方法统率具体知识的掌握和具体问题的解法，循此培养和发展学生的数学能力.

4.2.2 不足之处

1)预设与生成很难一致；

2)采用变式教学对学生的思维要求较高，部分学生很难达到；

3)学生自主探究多了，时间的分配自然成了问题.

最后笔者想说：在许多人心目中,数学就是一堆数字、符号和图形，它很抽象、深奥甚至神秘.其实数学经历了几千年的文化积淀，才汇聚成今天人类知识海洋的重要组成部分.让我们为孩子提供自主探索、合作交流的舞台，为每一个孩子积淀爱心、信心，把枯燥乏味的数字、符号、图形变成跳动的音符，与孩子共同享受艺术般的快乐吧！