渐近非扩张映射不动点与均衡解的公共迭代Halpern型方法*

王元恒, 陈灵法

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

设N为正整数集且R为实数集,H为带有内积(·,·)和范数‖·‖的实Hilbert空间,C⊆H为非空闭凸子集.用⇀和→分别表示弱收敛和强收敛.映射T:C→C为自映射,且F(T)表示映射T的不动点集，即F(T)={x∈C:Tx=x}.若满足

‖Tx-Ty‖≤‖x-y‖, ∀x,y∈C,

则称映射T为非扩张映射.若存在数列{kn}⊂[1,∞)，kn→1(n→∞),并且满足

‖Tnx-Tny‖≤kn‖x-y‖, ∀x,y∈C,

则称映射T为具有系数列{kn}的渐近非扩张映射.显然,若kn≡1,则渐近非扩张映射T为非扩张映射.

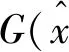
,y)≥0, ∀y∈C.

(1)

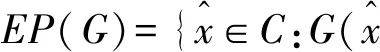
均衡问题、变分不等式问题、不动点问题等是非线性分析中的一些基本问题,在电路分析、大范围经济理论、力学、图像处理、最优化理论及非线性分析自身发展中有着广泛的应用,从而引起了许多学者对这些问题解的存在性和计算方法的广泛研究[1-13].其中,Halpern型迭代方法已经向黏滞的、隐形的、多重的等迭代方法发展,通过附加某些条件得到相应的收敛性,并且用各种迭代程序求不动点集和均衡问题解的公共元.

2013年,Chuang等[14]研究了用下列迭代程序求关于带扰动的拟非扩张映射的不动点集和均衡问题解的公共元:

并证明了该序列在一些确定条件下是强收敛的.

2010年,Lou等[15]证明了由黏性迭代式xn+1=αnf(xn)+(1-αn)Tnxn生成的{xn}强收敛到渐近非扩张映射T的不动点.2017年,Fan等[16]研究了下列迭代方程：

并证明了此迭代序列{xn}强收敛到非扩张映射T的不动点x*.

在上述工作的激励下，笔者研究用下面新的三步Halpern型迭代程序求关于渐近非扩张映射的不动点和平衡问题解的公共元:

(2)

式(2)中:C⊂H为非空有界闭凸子集;T:C→C为具有系数列{kn}的渐近非扩张映射;{αn},{βn},{λn},{γn}为(0,1)上的实数列;{ξn}⊂[a,+∞),a>0.并且在较弱条件下证明了该迭代系列{xn}的强收敛性定理.本文将不动点问题与均衡问题相结合，并将非扩张映射推广到渐近非扩张映射，迭代过程也推广到了三步迭代法，从而推广或部分推广了许多文献的主要结果[1,3-5,7-9,11-16].

1 预备知识

以下总设H为实Hilbert空间,C⊂H为非空闭凸子集.对∀x∈H,若PC:H→C,PC(x)∈C满足

‖x-PCx‖≤‖x-y‖, ∀y∈C,

则称PC为度量投影,且PC(x)是唯一存在的.

引理1[17]不等式‖x+y‖2≤‖x‖2+2(y,x+y),∀x,y∈H恒成立.

引理3[14]设C⊂H为非空有界闭凸子集,令T:C→C为渐近非扩张映射且F(T)≠Ø,若xn⇀x且(I-T)xn→y,则 (I-T)x=y.

设C⊂H为闭凸子集,令G:C×C→R为二元函数,为解决均衡问题,总假设G:C×C→R满足下列条件：

(A1)对∀x∈C,G(x,x)=0;

(A2)G是单调的,即对∀x,y∈C,G(x,y)+G(y,x)≤0;

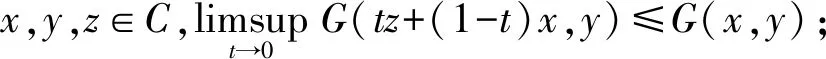
(A4)对每个x∈C,G(x,·)为凸下半连续的.

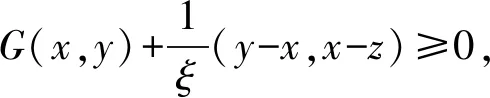
引理5[19]设二元函数G:C×C→R满足条件(A1)～(A4).对ξ>0和z∈H,定义映射Tξ:H→C为

则下列结论成立:

1)Tξ是强非扩张的,即‖Tξz1-Tξz2‖2≤(Tξz1-Tξz2,z1-z2),∀x,y∈C;

2)Tξ是单值的;

3)EP(G)是C的闭凸子集;

4)EP(G)=F(Tξ).

2 主要结果

定理1设H为实Hilbert空间，C⊂H为非空有界闭凸子集且θ∈C.设二元函数G:C×C→R满足条件(A1)～(A4).令T:C→C为具有系数列{kn}的渐近非扩张映射,且Ω=F(T)∩(EP)≠Ø.假设{αn},{βn},{λn},{γn}为(0,1)上的实数列,{ξn}⊂[a,+∞),a>0.令{xn}为由式(2)迭代生成的序列.若其迭代系数序列满足:

(6)

则序列{xn}强收敛到T的不动点和均衡问题(1)解的公共元x*∈F(T)∩EP(G).

证明 证明过程将分成5步.

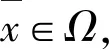
(7)

由式(2)和式(7)可以得到

(8)

从式(8)可以得出

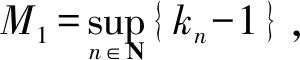
从而可以根据归纳法得到

所以得到 {xn}有界,进而{qn},{zn}和{Tnyn}也有界.

第2步 证明‖xn+1-xn‖→0.当n→∞时,根据迭代式(2)可以得到下面等式:

zn+1-zn=(1-αn+1)xn+1+αn+1Tn+1yn+1-(1-αn)xn-αnTnyn=

(1-αn+1)xn+1-(1-αn)xn+1+(1-αn)xn+1-(1-αn)xn+

αn+1Tn+1yn+1-αnTn+1yn+1+αnTn+1yn+1-αnTnyn=

(1-αn)(xn+1-xn)-(αn+1-αn)xn+1+αn(Tn+1yn+1-Tnyn)+(αn+1-αn)Tn+1yn+1=

(1-αn)(xn+1-xn)-(αn+1-αn)xn+1+αn(Tnyn+1-Tnyn)+

(αn+1-αn)Tn+1yn+1+αn(Tn+1yn+1-Tnyn+1),

从而

‖zn+1-zn‖≤(1-αn)‖xn+1-xn‖+|αn+1-αn|‖xn+1‖+αn‖Tnyn+1-Tnyn‖+

|αn+1-αn|‖Tn+1yn+1‖+αn‖Tn+1yn+1-Tnyn+1‖≤

(1-αn)‖xn+1-xn‖+|αn+1-αn|‖xn+1‖+αnkn‖yn+1-yn‖+

|αn+1-αn|‖Tn+1yn+1‖+αn‖Tn+1yn+1-Tnyn+1‖≤

(1-αn)‖xn+1-xn‖+|αn+1-αn|‖xn+1‖+|αn+1-αn|‖Tn+1yn+1‖+

αn‖Tn+1yn+1-Tnyn+1‖+αnkn(1-γn+1)‖xn+2-xn+1‖+

αnknγn‖xn+1-xn‖+αn‖Tn+1yn+1-Tnyn+1‖≤

(1-αn+αnknγn)‖qn+1-qn‖+|αn+1-αn|‖xn+1‖+|αn+1-αn|‖Tn+1yn+1‖+

αn‖Tn+1yn+1-Tnyn+1‖+αnkn(1-γn+1)‖qn+2-qn+1‖.

(9)

并且,

qn+2-qn+1=(1-βn+1)(λn+1qn+1)+βn+1zn+1-(1-βn)(λnqn)-βnzn=

λn+1qn+1-βn+1λn+1qn+1+βn+1zn+1-λnqn+βnλnqn-βnzn=

λn+1qn+1-λn+1qn+λn+1qn-λnqn-βn+1λn+1qn+1+βnλnqn+1-βnλnqn+1+

βnλnqn+βn+1zn+1-βn+1zn+βn+1zn-βnzn=

λn+1(qn+1-qn)+(λn+1-λn)qn-(βn+1λn+1-βnλn)qn+1-βnλn(qn+1-qn)+

βn+1(zn+1-zn)+(βn+1-βn)zn=

(λn+1-βnλn)(qn+1-qn)+(λn+1-λn)qn-(βn+1λn+1-βnλn)qn+1+

βn+1(zn+1-zn)+(βn+1-βn)zn.

(10)

因此,由式(9)和式(10)得到

‖qn+2-qn+1‖≤|λn+1-βnλn|‖qn+1-qn‖+|λn+1-λn|‖qn‖+

|βn+1λn+1-βnλn|‖qn+1‖+βn+1‖zn+1-zn‖+|βn+1-βn|‖zn‖≤

|λn+1-βnλn|‖qn+1-qn‖+|λn+1-λn|‖qn‖+|βn+1λn+1-βnλn|‖qn+1‖+

|βn+1-βn|‖zn‖+(βn+1-βn+1αn+βn+1αnknγn)‖qn+1-qn‖+

βn+1|αn+1-αn|‖Tn+1yn+1‖+βn+1αn‖Tn+1yn+1-Tnyn+1‖+

βn+1αnkn(1-γn+1)‖qn+2-qn+1‖+βn+1|αn+1-αn|‖xn+1‖=

(|λn+1-λnβn|+βn+1-βn+1αn+βn+1αnknγn)‖qn+1-qn‖+|λn+1-λn|‖qn‖+

βn+1|αn+1-αn|‖Tn+1yn+1‖+|βn+1λn+1-βnλn|‖qn+1‖+|βn+1-βn|‖zn‖+

βn+1αn‖Tn+1yn+1-Tnyn+1‖+βn+1|αn+1-αn|‖xn+1‖+βn+1αnkn(1-γn+1)‖qn+2-qn+1‖.

从而

(1-δn)‖xn+1-xn‖+M(|λn+1-λn|+|βn+1-βn|+

2βn+1|αn+1-αn|+|λn+1βn+1-λnβn|+βn+1αn)≤

(1-δn)‖xn+1-xn‖+M(2|λn+1-λn|+2|βn+1-βn|+2|αn+1-αn|+βn+1αn).

于是，利用引理2得到‖xn+1-xn‖→0,n→∞.

第3步 证明‖xn-Txn‖→0.根据迭代式(2)可以得到

‖qn+1-zn‖=‖(1-βn)(λnqn)+βnzn-zn‖=(1-βn)‖λnqn-zn‖.

由式(3)知，当n→∞时,‖qn+1-zn‖→0,并且当n→∞时，

‖yn-xn‖=‖γnxn+(1-γn)xn+1-xn‖≤|1-γn|‖xn+1-xn‖⟹‖yn-xn‖→0.

再由迭代式(2)可得,当n→∞时，

‖zn-xn‖=‖(1-αn)xn+αnTnyn-xn‖=‖-αnxn+αnTnyn‖≤|αn|‖-xn+Tnyn‖⟹‖zn-xn‖→0.

又因为

‖zn-Tnyn‖=‖(1-αn)xn+αnTnyn-Tnyn‖=(1-αn)‖xn-Tnyn‖≤

(1-αn)‖xn-xn+1‖+(1-αn)‖xn+1-Tnyn‖≤(1-αn)‖qn-qn+1‖+(1-αn)‖qn+1-Tnyn‖,

所以

‖qn+1-Tnyn‖=‖qn+1-zn+zn-Tnyn‖≤‖qn+1-zn‖+‖zn-Tnyn‖≤

‖qn+1-zn‖+(1-αn)‖qn-qn+1‖+(1-αn)‖qn+1-Tnyn‖.

这意味着

综上可得,当n→∞时,‖qn+1-Tnyn‖→0.又由迭代式(2)得

‖xn-Tnxn‖≤‖qn-Tnqn‖=‖qn-qn+1+qn+1-Tnyn+Tnyn-Tnqn‖≤

‖qn-qn+1‖+‖qn+1-Tnyn‖+‖Tnyn-Tnqn‖≤‖qn-qn+1‖+‖qn+1-Tnyn‖+kn‖yn-qn‖.

从而,当n→∞时,

‖xn-Tnxn‖→0.

因为T为渐近非扩张映射,所以

‖xn+1-Txn+1‖≤‖qn+1-Tqn+1‖=‖qn+1-Tn+1qn+1+Tn+1qn+1-Tqn+1‖≤

‖qn+1-Tn+1qn+1‖+‖Tn+1qn+1-Tqn+1‖≤‖qn+1-Tn+1qn+1‖+k1‖Tnqn+1-qn+1‖=

k1‖Tnqn+1-Tnqn+Tnqn-qn+qn-qn+1‖+‖qn+1-Tn+1qn+1‖≤

‖qn+1-Tn+1qn+1‖+k1‖Tnqn+1-Tnqn‖+k1‖Tnqn-qn‖+k1‖qn-qn+1‖≤

‖qn+1-Tn+1qn+1‖+k1kn‖qn+1-qn‖+k1‖Tnqn-qn‖+k1‖qn-qn+1‖.

综上所述,得到了当n→∞时,‖xn-Txn‖→0.

第4步 证明xn→x*∈F(T).因为{xn}有界,所以在Hilbert空间中,存在弱收敛子列{xni},令它收敛到x*,记为xni⇀x*∈H.根据引理3可得x*∈F(T).对n≥1，令wn=(1-βn)qn+βnzn,由迭代式(2)可得

qn+1=wn-(1-βn)(1-λn)qn.

已知{xn}有界,并根据式(3)可知,当n→∞时,

‖qn+1-wn‖=(1-βn)(1-λn)‖qn‖⟹‖qn+1-wn‖→0.

(11)

所以,存在子列{wni},使得wni⇀x*.并且当n→∞时,

qn+1=wn-(1-βn)(1-λn)qn=(1-(1-βn)(1-λn))wn-(1-βn)(1-λn)(qn-wn)=

(1-(1-βn)(1-λn))wn-(1-βn)(1-λn)βn(qn-zn).

(12)

由引理1知,

‖wn-x*‖2=‖(1-βn)qn+βnzn-x*‖2=‖(qn-x*)-βn(qn-zn)‖2≤

‖qn-x*‖2-2βn(qn-zn,wn-x*).

再根据引理1、式(11)和式(12)可以得到

‖xn+1-x*‖2≤‖qn+1-x*‖2=

‖(1-(1-λn)(1-βn))(wn-x*)-(1-λn)(1-βn)βn(qn-zn)-(1-λn)(1-βn)x*‖2≤

(1-(1-λn)(1-βn))2‖wn-x*‖-2(1-λn)(1-βn)(βn(qn-zn)+x*,qn+1-x*)≤

(1-(1-λn)(1-βn))‖wn-x*‖-2(1-λn)(1-βn)βn(qn-zn,qn+1-x*)-

2(1-λn)(1-βn)(x*,qn+1-x*)≤

(1-(1-λn)(1-βn))(‖qn-x*‖2-2βn(qn-zn,wn-x*))-

2(1-λn)(1-βn)βn(qn-zn,qn+1-x*)-2(1-λn)(1-βn)(x*,qn+1-x*)≤

(1-σn)‖qn-x*‖2+σn(-2βn(qn-zn,wn-x*))-

2βn(qn-zn,qn+1-x*)-2(x*,qn+1-x*)=(1-σn)‖qn-x*‖2+σnρn.

且

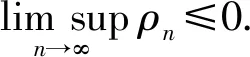
第5步 证明xn→x*∈EP(G).因为xn=Tξnqn,所以对任意y∈C有

由条件(A2)可得

用ni代替n,得到

对所有的t∈(0,1]和y∈C,令xt=ty+(1-t)x*,则对∀xt∈C,

因为‖xni-qni‖→0,并且xni⇀x*，所以由条件(A4)可以得到0≥G(xt,x*),n→∞.再由条件(A1),(A4)可知0=G(xt,xt)≤tG(xt,y)+(1-t)G(xt,x*)≤tG(xt,y),t>0.因此,

0≤G(xt,y).

令t→0,对每个y∈C有0≤G(x*,y),这意味着xn→x*∈EP(G).

总之,xn→x*∈F(T)∩EP(G).定理1证毕.

3 结 语

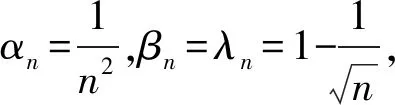
并且容易验证

所以,正是对迭代系数列{αn},{βn},{λn}的条件要求苛刻,才能使我们创造出这样一类新的与以往不同的迭代逼近算法,并且得到的结果也比较深刻,可以把对非扩张映射问题的研究推广到渐近非扩张映射,把迭代步骤推广到三步迭代格式,把均衡解问题和不动点问题结合起来考虑它们公共元的迭代方法,并在较弱的条件下证明了该迭代序列的强收敛性,其结果具有更广泛的适应性.例如,在本文定理1中,当取γn=0,且un=λnqn时,即为文献[5]所给的主要结果;当取γn=0，均衡函数G≡0时，即为文献[7]中所给的主要结果.所以,本文的结果推广或部分推广了近代许多文献的相应结果[1,3-5,7-9,11-16].