基于数字全息和计算全息的动态三色全息三维显示*

胡杰康， 王 辉， 李 勇， 吴 琼

(1.浙江师范大学 信息光学研究所,浙江 金华 321004;2.浙江省光信息检测与显示技术研究重点实验室,浙江 金华 321004)

0 引 言

目前，三维(three-dimension,3D)显示技术正以前所未有的速度进步，体三维显示[1]、双目视差立体显示[2]、多视点立体显示[3]等传统的三维显示技术已经得到了有效应用.所有这些传统的三维显示，其特点都是在技术上实现相对容易，但显示的三维景象很不自然，有的容易使人产生视觉疲劳甚至晕眩.光学全息成像技术的特点是能够再现光场完整的振幅和相位信息，观看全息再现的三维像与观看真实物体或场景的效果是一样的，所以全息三维显示是真正的3D技术，也是人们一直以来追求的重要三维显示目标[4-5].随着计算机和光电成像技术的迅速发展，利用数字全息和计算全息进行实时三维显示的研究引起了人们极大的关注.

数字全息术是利用光电传感器件记录全息图，然后通过计算机模拟光学衍射过程来实现被记录物体数字再现像的过程和技术[6].数字全息技术的特点是充分利用光电成像和计算机技术，使得全息图可以数字化重构，为三维定量测量提供了全新的路径[7-8].计算机制全息技术是将物光波的复振幅由计算机编码成为计算全息图(computer generated hologram,CGH)[9]，CGH可以输出到空间光调制器(space light modulator,SLM)中进行光学再现显示.CGH不仅能记录实际物体发出光波的振幅和相位，还能模拟出实际不存在物体的波前，因此,具有独特的优势和很好的灵活性[10-11].

数字全息技术和计算全息技术分别可以用于全息三维显示.Xu[12]和Sasaki等[13]基于计算全息用多个 SLMs重建了全视差全息视频.Kozacki等[14]和Matoba等[15]利用数字全息术实现了动态三维像的重构.Matsushima等[16]利用数字全息图数值再现的物光波和虚拟物光波相融合制作CGH，实现了大视角静态全息再现像的重构，增强了静态物体的显示效果.何泽浩等[17]论述了全息光学在虚拟现实(virtual reality,VR)与增强现实(augmented reality,AR)产业中的巨大优势，为全息光学中的AR/VR技术发展提供了新的方向.

本文在动态全息方面展开研究，设计并实现了一个将数字全息术与计算机全息术相结合的动态三色全息显示系统，用于显示由虚拟和真实物体组成的三维图像.将数字全息图实时加载到一个空间光调制器中,实现对真实物体的光学再现，将计算机生成的2个计算全息图分别加载到另外2个空间光调制器中,实现对虚拟对象的光学再现，在计算全息中可加入坐标文字等虚拟信息，三幅重建的图像在空间中融合，最终实现三色的三维显示，增强真实物体的三维显示效果，达到增强现实的目的.

1 数字全息图与计算全息图再现像的融合分析

由于数字全息图和计算全息图是通过不同方式得到的，为了使其再现像达到预期融合的效果，数字全息图和计算全息图的相关参数必须相匹配.

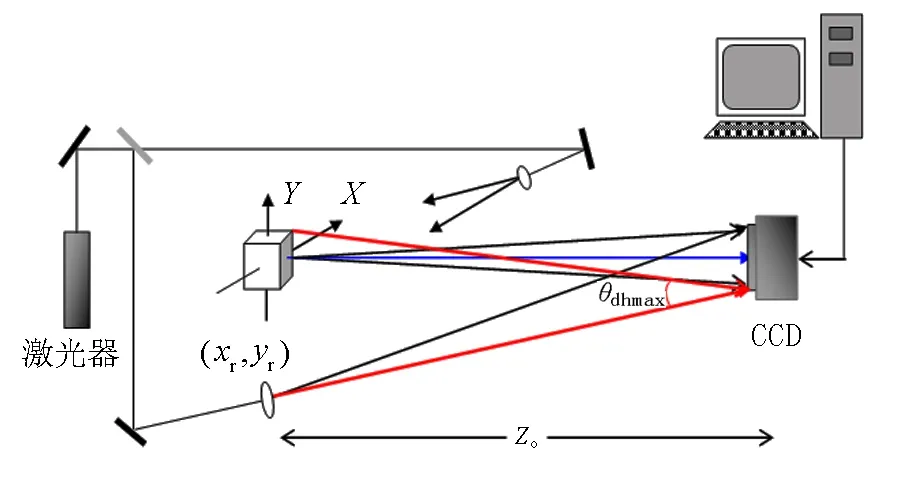
图1 数字全息记录光路原理图

1.1 数字全息记录条件及其参数

众所周知，利用无透镜傅里叶变换全息光路记录数字全息图可以获取最多目标的信息[18].图1是无透镜傅里叶变换全息记录光路原理图，样品中心和记录器件中心连线为光轴，即z轴，参考光源的点坐标为xr=0,yr=zr=zo.

设物体的复振幅反射率为ρ(xo,yo,zo)，物光波传播到记录平面时，复振幅分布O(xh,yh)可以表述成

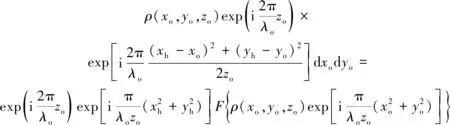
(1)

式(1)中，F{}表示傅里叶变换运算符.为了简化问题，本文仅讨论一维的情况，并且将物体近似为一个平面.在一维情况下,式(1)可以简化为

(2)

(3)

(4)

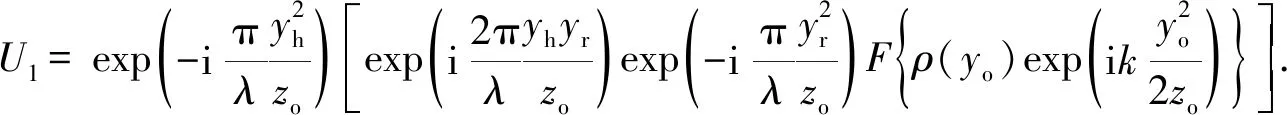
(5)

(6)

下面以原始像光波的成像说明其傅里叶变换的特性.考察与全息图距离为zo的平面(Xi,Yi)上的光分布：

(7)

(8)

可以看出，之所以称作无透镜傅里叶变换全息，是因为这种记录方式的再现像和其全息图之间存在傅里叶变换关系.同样可以得到零级项光波和共轭像光波在像面上的分布分别为：

(9)

(10)

从式(8)和式(10)可以看出，2个互为共轭的像分居零级两侧，相对yi=0点分别位移了yr和-yr.零级项再现光波式(9)核心部分是原物光波O(yh)模平方的傅里叶变换，根据傅里叶变换的卷积性质，式(9)表示的是处于像面中心的宽度为物体宽度2倍的光斑.

设物体在Y方向的最大宽度为Loymax.显然,若要使得再现像与零级光斑不重叠，则要求

|yr|≥3Loymax/2.

(11)

进一步考虑数字全息图记录器件本身的分辨率对物体大小的限制，全息图本质是记录物光波与参考光波的干涉图，对于无透镜傅里叶变换全息图，若物体最大宽度为Loymax，则相邻干涉条纹的间隔为

(12)

根据抽样定理，δ必须大于全息图记录器件抽样间隔的2倍，设记录器件的像素间隔为ΔCCD，则要求

(13)

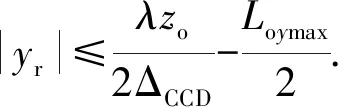
(14)

假设有一个极限情况，即设参考光的点源坐标为|yr|=3Loymax/2，则有

(15)

全息图再现物像关系为[19]

(16)

式(16)中:m是全息图的放大率；xc,yc,zc是再现光源的点坐标.

对于无透镜傅里叶变换全息图zr=zo，用点源坐标为xc=0,yc=0,zc=-zr的点光源垂直入射全息图，式(16)可以简化为

(17)

(18)

1.2 计算全息的参数设定

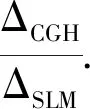
设计算全息图的模拟物光波分布为O(xh,yh)，模拟参考光为R(xh,yh)，原理上计算机制全息图就是计算式(3)的分布，有各种方法计算全息图，其中一个最为直接的方法按照下式计算：

Ih=α+2|O(xh,yh)|cos[φr(xh,yh)-φo(xh,yh)].

(19)

I(xh,yh)=0.5{1+A(xh,yh)cos[φr(xh,yh)-φo(xh,yh)]}.

(20)

式(20)中的第2项贡献了物光波的全部信息，这种编码方法称作博奇型计算全息图.当采用式(20)计算全息图时，由于其再现像平面不存在零级卷积散斑，此时,参考光的点源坐标yrCGH和物体宽度LoyCGHmax的关系只要满足

|yrCGH|≥LoyCGHmax/2,

(21)

再现的2个共轭像就不会重叠.为了满足全息图抽样间隔ΔCGH=ΔCCD对干涉条纹空间频率的显示，此时同样必须满足式(14)的条件，在参考光的点源坐标选取极限的情况下，即当|yrCGH|=Loymax/2时,有

(22)

与式(15)相比，计算全息所能记录物体的宽度可以达到数字全息的2倍.需要说明的是，当物体的大小刚好选取式(15)和式(22)的最大值时，全息图干涉条纹的一个周期内恰好有2个像素，由于记录器件靶面的不均匀性及电子噪音的影响，此时得到的全息图质量难以保证.在实际应用中，为了确保得到较好的数字全息图，可以设定相邻干涉条纹的间隔为4个像素，此时可以将式(15)和式(22)修正为:

(23)

(24)

2 实验与结果

2.1 记录无透镜傅里叶变换数字全息图

图2 骰子的数字全息图

2.2 CGH的计算

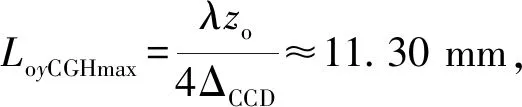
(a)二维坐标框架 (b)二维字符“骰子” (c)期望的融合像

根据计算全息原理，编制无透镜傅里叶变换全息计算程序，采用云点计算，首先将图3(a)和图3(b)转换为空间坐标数据(x,y,z,A),x,y,z是图中任一点的坐标，A是对应点的振幅.计算参数与数字全息图光路一致，即xr=0,yr=8.0 mm,zr=zo，字符“骰子”计算波长为520 nm，坐标框架计算波长为462 nm.

2.3 数字全息图和计算全息图的光学再现

图4是实现本文提出的数字全息和计算全息融合的增强现实的光路原理图.利用3片式投影仪中3个投影芯片SLM1,SLM2和SLM3分别显示数字全息图和计算机制全息图(CGH)，为了增强显示效果，使用不同颜色的激光再现3个全息图.图中虚框部分是记录数字全息图的光路，记录得到的数字全息图由计算机送入SLM3.计算机计算不同虚拟物体的CGH1和CGH2，分别输入SLM1和SLM2.激光器1、激光器2和激光器3为不同颜色的激光器.激光器1和激光器2发出的光分别用于再现CGH1和CGH2；激光器3既是数字全息图的记录光源，同时其分束光经M6反射后入射到SLM3作为再现数字全息图的照明光源.

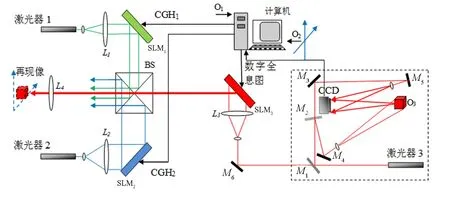
图4 数字全息和计算全息融合的增强现实的光路原理图

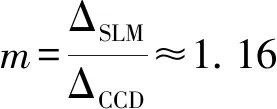
图5给出了实验结果.图5(a)～(c)3个全息图通过各自的再现通道分别再现了像的照片，图5(d)是3个通道同时再现像的照片.

图5 数字全息图和计算全息图融合的再现像

根据上述得到的实验结果,将数字全息记录得到的数字全息图和计算得到的CGH同时输入到空间光调制器中进行光学再现，拍摄得到相应的实验结果如图6所示.图6(a)～(c)是不同时间点的再现像照片.实验结果证明,本文提出的方案是可行的.

图6 数字全息图和计算全息图融合的动态再现像

3 结 论

本文提出将数字全息和计算全息同时输入到空间光调制器进行光学再现，以实现实际三维物体的像和虚拟物体的再现像相融合达到现实增强的目的.通过实验，证实了数字全息图和计算机制全息图输入空间光调制器实现再现像融合的可行性，得到很好的光学再现像.本文对数字全息和计算全息的综合应用进行了有益的尝试，对数字化全息术在现实增强方面的应用进行了初步探索，对于全息三维影视和全息动态显微技术的发展具有重要的启示和参考价值.