计算全息图的基本理论与制作＊

覃 芳

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

随着数字计算机与计算机技术的迅速发展，人们广泛地使用计算机去模拟、运算、处理各种光学过程。在计算机科学和光学相互促进和结合的发展进程中，1965年德国光学专家罗曼（Lohmann A W）使用计算机和计算机控制的绘图仪做出了世界上第一个计算全息图。计算全息图不仅可以全面地记录光波的振幅和相位，而且能够记录综合复杂的，或者世间不存在物体的全息图，因而具有独特的优点和极大的灵活性。从光学发展的历史上看，计算全息首次将计算机引入光学处理领域。很多光学现象都可以用计算机来进行仿真，计算全息图成为数字信息和光学信息之间有效的联系环节［1］。传统的全息技术是用光学的办法，用干涉记录的方法制作全息图。计算全息是用计算机编码制作全息图，把无波的数学描述输入数字计算机处理后，直接产生全息图，代替了用光学设备实地记录，既可以完全节省光源且对光学设备的精度要求不高，又能制作实际并不存在的各种物体的全息图，且噪声低，重复性高，比光学全息具有明显的简易性和灵活性［2－4］。

由于计算全息图的这些优点，再加上计算机的处理速度和存储性能的不断提高，因此绘图技术的不断发展以及多种编程语言的广泛应用都给计算全息的发展与应用带来新的突破和发展。在杂志、书刊上发表的文章也很多，广泛地研究着计算全息的各个课题。这些不同的研究可粗略地分为三个方面：（1）计算全息图制作的算法，主要研究新的算法以提高计算的速度。文献［5］提出了一种制作计算全息干涉图的基于牛顿迭代法的新算法，该算法高效快捷。文献［6］提出了一种快速、简易的计算机制作全息图的方法。（2）提高计算全息图的质量，降低其再现波面的误差。文献［7］利用数字图像处理的方法对计算全息图进行滤波处理，消除了零级像和原始像，使数字再现时得到了清晰的再现像。文献［3］采取一系列提高计算全息图质量的措施，有效地消除了零级像和孪生像的影响，获得了清晰的数字再现像。（3）计算全息技术的应用。文献［8］中提出一种基于傅里叶变换印刷全息标识防伪方法，通过数字印刷技术将加密的傅里叶变换全息标识印制在证件等印刷品上作为防伪标识，具有重要的实用意义。文献［9］将计算全息技术应用于图像加密，提高了图像系统的保密性能。文献［10］开发了一种新的基于计算全息技术的3D动态显示系统。文献［11］、［12］中计算全息图已经成功应用于全息视频显示系统。文献［13］中介绍了计算全息图在光学神经网络中的应用。文献［14］提出了计算全息术应用于非球面检测的展望。文献［15］将计算全息术应用在非球面检测中。

文中首先介绍计算全息的基本理论，然后采用李威汉的编码方法分别制作了傅里叶二元计算全息图和菲涅耳二元计算全息图，并将全息图在实际光路中再现，再现像明显直观。

1 计算全息的基本理论

计算全息图制作的主要步骤：（1）对物面按抽样定理进行抽样，得到其在各个离散点上的离散值；（2）计算全息平面上的光强的分布；（3）根据各种不同的编码方法将全息平面上的光场分布用计算全息图的透过率表示出来；（4）用绘图仪、阴极射线管或者计算机控制的微密度计绘制全息图，也可用特殊输出直接把全息图记录在胶片上［3］。

1.1 记录对象［4］

计算全息图可分为像计算全息图，傅里叶变换计算全息图和菲涅耳计算全息图3种。（1）像计算全息图直接记录物体的像场分布。像计算全息图可再现物体本身，它广泛应用于干涉测试中。（2）傅里叶变换计算全息图记录物波函数的傅里叶变换谱。因此在制作此种计算全息图时，首先用计算机算出物波函数的离散傅里叶变换谱，这通常应用快速傅里叶变换算法。在MatLab中采用二维快速傅里叶变换函数fft2（）来计算，要注意使用移谱函数fftshift（）将频谱的低频部分移到中心，否则傅里叶频谱会被分裂。傅里叶变换计算全息图广泛应用于光学数据处理中的空间滤波器或其他变换运算，这是计算全息技术中应用最广泛的领域。（3）菲涅耳计算全息图记录物体发出的菲涅耳衍射波。在制作菲涅耳计算全息图时，首先求出物体发出的波前在某一特定距离平面上的菲涅耳衍射图的数字表达式。如果物体是二维的，则可用一个相当简单的积分式（1）计算波面的菲涅耳传播；对于三维物体，则需要的计算要复杂得多，菲涅耳计算全息图一般用于图像的三维显示技术中。

1.2 编码方法

在通讯中，编码指把输入信息变为信道上传递信号的过程。在计算全息中，输入信息是待记录的光波复振幅，而中间的传递介质是全息图，其信息特征是全息图上的透过率。将二维光场复振幅分布变换为全息图的二维透过率分布的过程，称为计算全息图的编码。可以用一个数学公式来描述这个编码过程：

式（2）中，hi（x，y）是计算全息图的全息函数，它应为实值非负函数；f（x，y）是输入的空间复值函数；C是相应于编码的变换符号；i表示不同的编码方法［16］。

有两种复值函数编码方法，第一种方法是把复值函数用两个实值非负函数来表示，即对幅值和位相进行编码；第二种编码方法即修正型离轴参考光计算全息图通过加进离轴参考光偏置，分别进行调幅和调相，变成实值非负函数。这样编码比第一种方法要简便，没有位相编码的问题，这是其优越之处，但由于加进了偏置分量，使得全息图要记录的空间带宽积大为增加，全息图上的抽样点数必须增加，同时也增加了计算全息图的绘图时间［4］。

对幅值和位相编码的典型方法有罗曼迂回相位编码和李威汉四阶迂回相位法。博奇编码是典型的修正型离轴参考光编码方法。

1.2.1 罗曼迂回相位编码［17，18］

罗曼根据不规则光栅的衍射效应提出了迂回相位编码。当光栅栅距变化时，某方向的衍射光波在该位置处引入相应相位延迟，因此通过局部改变光栅栅距的办法，可在某个衍射方向上得到所需要的相位调制。罗曼迂回相位编码在全息图的每个抽样单元中，放置一个通光孔径，通过改变通光孔径的面积来实现光波场的振幅调制，而通过改变通光孔径中心距抽样单元中心的位置来实现光场相位的编码。由于利用这种方法编码的计算全息图的透过率只有0、1两个值，故制作简单，抗干扰能力强，对记录介质的非线性效应不敏感，可多次复制而不失真，因而应用较为广泛。

1.2.2 李威汉四阶迂回相位法［4］

1970年，李威汉提出了一种新的计算全息制作法。李氏把全息图面上的每一个抽样单元细分为四个子单元，把复数样点值编码进这四个子单元中。实际上，这相当于在复平面上分解复矢量。复平面上有四个基矢：r＋＝（1，0），r－＝（－1，0），j＋＝（0，1），j－＝（0，－1），任何一个复数可表示为

而F1，F2，F3，F4全都是实的非负数。当然实际上至多只有两个分量为非零值。因此要描述一个样点的复振幅，只需要在两个子单元中用开孔大小或灰度等级来表示。

1.2.3 博奇编码方法［19］

光学离轴全息图，其通过率函数在线性记录条件下为

式（4）中，A（x，y）和R（x，y）分别为物光波和参考光波复振幅。前两项只对偏置分量有贡献，使h（x，y）为实的非负函数，只有最后一项才包含了物体的全部信息，前两项的偏置分量在制作全息图时对带宽增加了要求，在再现时会出现多余的衍射像。应用计算机制作全息图时，由于计算机灵活性的特点，可以通过加其他偏置分量来达到使h（x，y）为实的非负函数的目的，因此，用博奇提出的加直流偏置分量代替式中的前两项，利用计算机构成新的全息函数。

2 基于MatLab的计算全息图的制作［20－22］

计算全息图根据其透过率变化可分为二元计算全息图和灰阶计算全息图。灰阶计算全息图的振幅透过率函数是变化的，二元计算全息振幅透过率只有0或1两个值。但两者都保存了物波的全部信息，因此都能完整地再现原始物波。由于二元计算全息图的制作经济简便，同时抗外界噪声干扰的能力强，对照相底片的非线性效应不敏感，可以多次复制而不失真，因此二元计算全息图比灰阶计算全息图更有优点。

李威汉四阶迂回相位法相对于其他编码方法简单，目前尚未见用其制作计算全息图的文献。因此，基于MatLab平台采用李威汉四阶迂回相位法编码分别制作了傅里叶二元计算全息图和菲涅耳二元计算全息图。

2.1 待记录复振幅波面的抽样和量化

根据四阶迂回相位法，将待记录复振幅波面上的一个样点编码进四个子单元（列）中，而实际上只需要在两个子单元中用开孔大小或灰度等级来表示。对于二元计算全息图，应用开孔大小表示。开孔的大小由量化采用的方法决定，如图1所示：

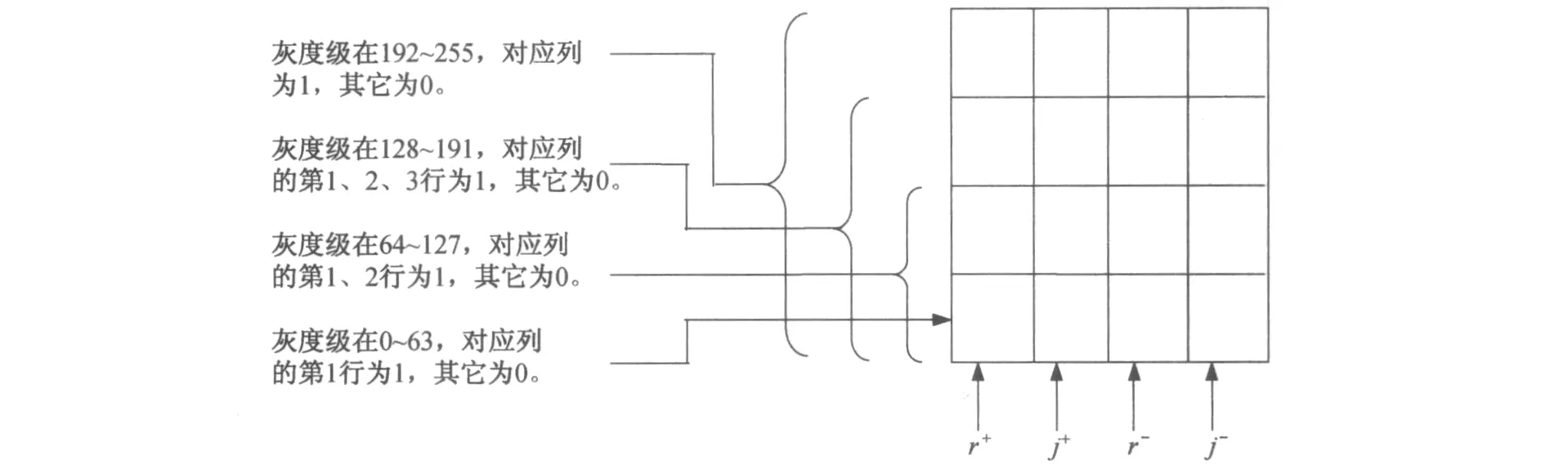
图1 复振幅波面样点的量化Fig.1 Quantization of the complex amplitude wavefront sample

2.2 傅里叶二元计算全息图的制作

傅里叶计算全息图的编程流程，如图2所示。

所用物波是一幅128×128的二维平面图像（见图3）。用MatLab中的二维快速傅里叶变换函数fft2（）计算物波傅里叶谱，并对其编码和量化后生成计算全息图（见图4）。取平行参考光垂直入射，再进行一次傅里叶变换，可数字再现原物波（见图5）。

图2 傅里叶计算全息图编程流程图Fig.2 Flow chart of Fourier CGH

图3 原图Fig.3 Original image

图4 计算全息图局部Fig.4 Part of CGH

图5 数字再现像Fig.5 Digital reconstruction image

2.3 菲涅耳二元计算全息图的制作

菲涅耳计算全息图的编程流程，如图6所示。

所用物波是128×128的二维平面图像（详见图7）。用式（1）计算物波衍射到1m处的波面，对其编码和量化后生成计算全息图（见图8）。取平行参考光垂直入射，计算距离为1m菲涅耳衍射，得到原物波数字再现像（见图9）。

图6 菲涅耳计算全息图编程流程图Fig.6 Flow chart of Fresnel CGH

计算全息图和菲涅耳二元计算图。再现实验得到的再现像明显、直观。计算全息图灵活性极高，制作简单，但它也存在不足之处。由于计算机存储容量，绘图仪和CRT显示器等的分辨力有限，因此要制作一张空间带宽积很大的计算全息图是费时和困难的。然而，电子技术和计算机技术的不断发展终将带来大存储容量的计算机和高分辨力的绘图仪及显示器。另外，越来越多的专家和学者对计算全息图各个课题的研究都会使计算全息的应用越来越广泛。

［1］ 苏显渝，李继陶.信息光学［M］.北京：科学出版社，1999.

［2］ FENG Y J，DING J P，ZHOU J.Self－focusing matched filter produced by computer－generated hologram［J］.OpticsCommunications，2000，184：89－93.

［3］ 赵付丽，章鹤龄，邢敬婷，等.基于MatLab的计算全息图的制作与数字再现的研究［J］.应用光学，2009，30（6）：953－957.

［4］ 虞祖良，金国藩.计算机制全息图［M］.北京：清华大学出版社，1984.

［5］ 陈家祯，郑子华，陈利永.基于牛顿迭代法的计算全息干涉图仿真［J］.计算机仿真，2005，22（12）：178－184.

［6］ 甘亮勤，杜旭日，曾胜财，等.计算全息图快速实现的研究［J］.厦门理工学院学报，2010，18（1）：36－38.

［7］ 赵雅晶，钟金刚.黄氏傅里叶计算全息图的数字再现及零级像的消除［J］.光子学报，2004，33（11）：1339－1342.

［8］ 孙刘杰，庄松林.基于加密傅里叶变换全息印刷防伪技术研究［J］.光学仪器，2006，28（1）：69－73.

［9］ 张秋霞.一类光学系统计算全息图像加密技术研究［J］.信息技术，2010（2）：33－35.

［10］ XU X W，SOLANKI S.Computer－generated holography for dynamic display of 3Dobjects with full parallax［J］.TheInternational JournalofVirtualReality，2009，8（1）：33－38.

［11］ YAMAGUCHI T，OKABE G，YOSHIKAWA H.Real－time image plane full－color and full－parallax holographic video display system［J］.OpticalEngineering，2007，46：125801－1－125801－8.

［12］ SMITHWICK Q Y J，SMALLEY D E，BOVE J V M，etal.Progress in holographic video displays based on guided－wave acousto－optic devices［J］.SPIE，2008，6912：69120H－1－69120H－10.

［13］ KAIKHAH K，LOOCHAN F.Computer generated holograms for optical neural networks［J］.AppliedIntelligence，2001，14（2）：145－160.

［14］ TIZIANI H J.Prospects of testing aspheric surfaces with computer－generated holograms［J］.SPIE，1980，235：72－79.

［15］ 卢振武，刘 华，李凤有.利用曲面计算全息图进行非球面检测［J］.光学 精密工程，2004，12（6）：555－559.

［16］ 郑 宇.罗曼编码型计算全息图的制作［J］.TechnologyandMarket，2011，18（6）：8－9.

［17］ 杜志东，裴文荣，张 权.计算机制全息图探究及实现［J］.物理与工程，2010，20（2）：43－46.

［18］ 陈炳初，雷宏香，蔡志刚.用MatLab制作迂回相位编码的傅里叶变换计算全息图［J］.中山大学研究生学刊（自然科学、医学版），2006，27（2）：60－65.

［19］ BURCH J J.A computer algorithm for the synthesis of spatial frequency filters［J］.IEEE，1967，55（4）：599－601.

［20］ 钱晓凡，胡 涛，张 晔.基于MatLab的衍射场模拟计算［J］.昆明理工大学学报（理工版），2004，29（3）：132－134.

［21］ 肖 伟，刘 忠.MatLab程序设计与应用［M］.北京：清华大学出版社，2005.

［22］ 王炳武.MatLab 5.3实用教程［M］.北京：中国水利水电出版，2000.