滚控式变质心飞行器动力学特性分析与控制

范一迪，荆武兴，高长生，杜华军

(1. 哈尔滨工业大学航天工程系，哈尔滨 150001；2. 北京航天自动控制研究所，北京 100854)

0 引 言

近年来，高超声速再入机动飞行器在大气层再入任务中扮演着越来越重要的角色，而提高飞行器的控制能力是增强其机动性能必然面临的问题。多项研究表明，变质心控制技术相比其他传统控制技术(如空气舵控制、发动机控制等)具有低成本、高效率等优势[1-3]。变质心控制是通过调整飞行器内部质量分布改变系统质心位置，使得气动力臂发生变化，从而产生附加气动力矩控制飞行器姿态运动。因此，变质心飞行器凭借其气动布局简单、无舵面烧蚀、无燃料消耗等优势逐渐成为近年来航天控制领域研究的热点问题之一。

1980年，美国国家航空航天局(National Aeronautics and Space Administration，NASA)学者Anon在发表的一项通用大气进入研究报告中首次提出了变质心控制这一概念[4]，之后，美国海军水面作战中心(Naval Surface Warfare Center，NSWC)和桑迪亚国家实验室(Sandia National Laboratories，SNL)均开展了多项研究，成果显著[1,5-6]。1997年，俄罗斯研制的白杨M导弹成功运用了变质心控制产生控制力和控制力矩实现了弹道修正[7]。相比国外已进入工程实践的变质心控制技术研究，国内对该技术的研究仍处于系统动力学建模、机理分析、控制器设计等方面。较早涉及变质心研究的单位是西北工业大学，易彦等[8]利用拉格朗日法推导了变质心弹头的空间六自由度动力学模型，并仿真说明了滑块的运动能够改变飞行器的姿态；周敏等[9]基于固定配平型弹头单通道变质心滚转控制模式提出了一种螺旋机动控制方法；李瑞康等[10]研究了双滑块变质心飞行器的配平攻角与机动能力；周韬等[11]对三滑块变质心弹头静态控制性能进行了分析。高长生等[12]研究了径向滑块运动对自旋弹弹体性能的影响。当前国内对于变质心控制技术的研究仍处于探索阶段，目前的研究主要集中于多滑块的配平控制分析及控制器设计，而对单滑块滚控式变质心飞行器的机理分析、控制性能问题涉及较少。

本文首先针对滚控式变质心飞行器建立了包含滑块运动的七自由度完整动力学模型，讨论了其运动特性以及动力学系统的特点；其次结合频域分析法对滑块运动与载体姿态运动之间的耦合影响以及动态响应过程进行了分析，揭示了滚控式变质心飞行器的控制机理；最后通过对通道间的耦合效应的分析及控制能力的仿真提出了对飞行器结构设计和控制系统设计的相关要求，为滚控式变质心飞行器的工程实践提供一些理论参考。

1 动力学模型

1.1 系统动力学模型

滚控式单滑块构型模式的飞行器由底部削平的圆锥(或圆台)状载体和位于尾端的滑块组成，滑块位于系统质心后下方，由电机驱动，只能沿平行于削平面且垂直于载体中心线的方向平移运动，不可旋转。滑块相对载体的运动使得系统质心发生偏移，在气动力的作用下实现对飞行器滚转运动的控制。

本文的研究对象如图1所示，S,B,P分别表示系统、载体、滑块，b,s分别为载体质心和系统瞬时质心。由于滑块的质量和体积与载体相比较小，因此在建模过程中将其看作质点。

图1 滚控式模型示意图Fig.1 Moving-masses and body descriptions

定义惯性坐标系(OXYZ)、系统固连坐标系(osxsyszs)和载体固连坐标系(obxbybzb)分别如图1所示，其中系统固连坐标系的原点位于瞬时系统质心，且跟随弹体旋转。

定义变量符号：m表示质量，I表示转动惯量，下标S，B，P分别表示系统、载体和滑块；rbp表示从点b到点p的相对位置矢量，νb表示载体相对于惯性坐标系的速度，ωB/I表示载体固连坐标系相对于惯性坐标系的旋转角速度；G，Fa分别表示重力和作用在飞行器载体上的空气动力，MB表示空气动力对载体质心的气动力矩。

定义质量比：μP=mP/mS，μB=mB/mS。

因此，载体坐标系下系统质心和姿态动力学方程分别为：

(1)

(2)

式中:(·)×、(·)′、(·)″分别表示矢量的叉乘矩阵、矢量在载体坐标系下对时间的一阶、二阶导数。

由载体动力学方程可以看出滚控式变质心飞行器具有以下特点：

1) 和传统飞行器相比，变质心飞行器载体还受到滑块偏移产生的耦合作用，这些作用项将对载体姿态运动产生一定影响，因此，该系统是一个典型的非线性、强耦合的快时变复杂系统。

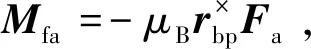
为了便于动力学分析，根据产生原因将方程(1)和(2)右边的附加力和附加力矩分成以下几项：

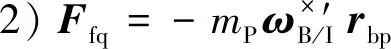
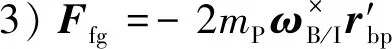
以上的力和力矩统称为附加惯性力和附加惯性力矩。

以上各项为滚控式变质心飞行器受到的特有的力和力矩。

从而，系统动力学方程可以表示为如下形式：

(3)

Mfg+Mfq+Mfr

(4)

1.2 滑块动力学模型

为了便于下文对执行机构控制能力受滑块质量影响的分析，此处建立滑块动力学方程。由于滑块相对载体只存在平移运动，且滑块的质量和体积相对载体来说较小，因此可将其看作质点，只需建立其质心平动动力学模型：

(5)

将表达式

(6)

表示在载体坐标系下并代入方程(5)可得：

(7)

将方程(1)代入式(7)即可得到载体坐标系下滑块动力学方程的矢量形式：

(8)

其中，方程右边的后三项即为载体姿态运动与滑块运动的耦合作用对滑块运动的影响项。

2 弹体姿态动力学分析

滚控式单滑块变质心飞行器的控制机理是：飞行过程中，面对称外形使得飞行器在稳定飞行条件下产生固定的配平攻角，通过伺服电机移动滑块位置，改变飞行器系统质心，利用气动配平力矩控制飞行器姿态。而由于升力方向始终位于弹体的纵对称面内，因此通过控制滚转角来控制升力的指向，实现机动飞行。

从弹体的姿态动力学方程可以看出，滑块的运动特性和总体参数是影响飞行器动力学性能的主要因素。因此，需要对飞行器所受力矩情况、动态响应特性以及控制能力等方面进行深入研究。

为了定量分析，作如下假设：

1) 忽略地球引力和地球自转角速度作用。

2) 根据所研究对象的运动特性认为飞行器在飞行过程中所经历的只是小角度摄动，因此飞行攻角α和侧滑角β均为小量，飞行速度分量νy，νz和角运动分量ωy，ωz均为小的摄动量。

3) 将滑块作为质点处理；由于滑块的偏移位移受到载体外形的限制，因此本文所设计的滑块偏移位移的幅值为±0.3 m；考虑到物理限制滑块位移和速度均为不大的值，基于此滑块运动导致系统转动惯量的变化可忽略，滑块运动给载体施加的作用力和气动外力相比可以忽略。

2.1 俯仰、偏航运动分析

基于上述假设，飞行器受到的气动力和气动力矩在载体坐标系下表示为：

(9)

(10)

因此系统的变质心方程可以简化成如下的形式：

(11)

(12)

式中：

根据速度系与载体系之间的转换关系，攻角和侧滑角可表示为：

(13)

利用假设条件(2)，将其线性化成如下形式：

(14)

对式(14)进行微分处理：

(15)

因此方程(11)、(12)的后两式可以写成：

(16)

(17)

将气动力和气动力矩的线性表达式(9)和(10)代入方程(16)和(17)左边项得到：

(18)

(19)

联立方程(16)和(18)可以得到：

(20)

对式(20)微分并与式(19)一同代入方程(17)，整理得到如下运动微分方程：

(21)

式中：

根据运动微分方程可知，由于A1，A2，C0只与飞行器的结构布局和外部流场有关，而与滑块的运动无关，因此对于已知结构布局的飞行器，存在一个固定的配平攻角，而滑块的运动并不影响其攻角的响应。对于弹道式再入飞行器，通过计算发现，A2<0,A21≪A22，因此可以认为A2≈A21，则稳态时攻角为：

(22)

式(22)表明，执行机构在飞行器内部的布局位置影响配平攻角的大小，这是因为执行机构的位置分布决定了滑块的位置，而滑块的位置影响了系统质心的位置，从而使得系统质心与压心之间的距离变化，导致配平攻角的不同。

根据对飞行攻角的分析，可以得到两点重要结论：1)在飞行器的外形和结构设计阶段需要充分考虑飞行攻角的需求，根据所需飞行攻角的范围合理配置执行机构在载体内部的位置。2)飞行攻角不受滑块运动的影响，因此在控制器的设计中可以认为飞行器具有俯仰稳定。

其次分析飞行器侧滑角的运动。从方程(21)第二式可以看出，由于气动阻力的存在，使得滑块的偏移在使得飞行器滚转角发生变化的同时，也对偏航通道产生影响。将侧滑角的运动方程用传递函数表示为：

(23)

假设滑块的伺服控制具有如下的输入输出关系：

(24)

式中：δzc表示滑块的指令输入。

由式(23)和式(24)得到：

β1(s)+β2(s)

(25)

对于一个阶跃输入信号：

(26)

代入式(25)，得到侧滑角时域响应：

(27)

(28)

式中：

对于弹道式再入飞行器，通过计算发现，B1>0,B21≫B22，因此可以认为B2≈B21，如mS=1000 kg,μP=0.3,Iy=1000 kg·m2,δz=0.1 m,lx=-0.5 m，ly=-0.3 m，v=4760 m/s时在飞行高度20 km，通过计算得到B1=4.719,B21=43.047,B22=0.953。

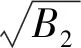
稳态时侧滑角为：

(29)

从式(29)可以看出，由于滚转和偏航通道间的耦合作用的存在，滑块的偏移在控制飞行器滚转角的同时也对侧滑角产生相应的扰动，而扰动的大小与飞行条件、飞行器外形和滑块布局模式密切相关。对于给定的飞行器外形和飞行条件，滑块偏移产生的侧滑角稳态值不仅与滑块的质量比和布局位置有关，还受到滑块横向偏移距离的影响，且滑块的质量比越大，滑块越远离载体质心，侧滑角扰动越大。因此，该耦合作用对控制器的设计提出了相应的要求：1)在控制滚转角达到指令值后应使得滑块恢复到稳定位置，以减弱侧滑角的扰动。2)为减弱扰动，滑块的偏移距离越小越好，但考虑到控制能力，减小偏移距离则需要增大滑块质量比，因此在飞行器设计过程中应合理选择二者的值。

2.2 滚转运动分析

为了分析滑块偏移使得飞行器发生滚转姿态变化的作用机理，首先设计系统状态反馈控制器，如图2所示，控制器的输入为飞行器实际滚转角与指令滚转角的偏差值。

图2 滚转控制框图Fig.2 Attitude control schematic map for roll angle

基于上文假设，在稳态配平条件下，飞行器滚转运动的动力学方程可以简化为：

(30)

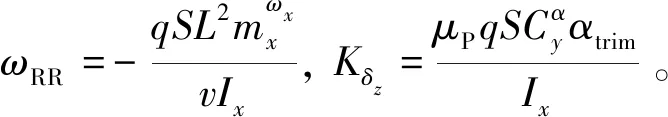
假设执行机构的动力学为二阶振荡环节，则整个系统的传递函数为：

(31)

写成状态空间的形式如下：

(32)

即：

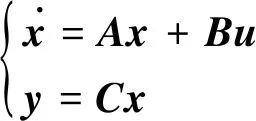
(33)

式中:y为输出向量。

选择状态反馈控制：

则整个系统的开环传递函数为：

TOL(s)=G(s)H(s)

(34)

其中，H(s)在式(31)中已给出，全状态反馈补偿器的传递函数G(s)为：

(35)

由于当开环传递函数的穿越频率高于被控系统最大极点时，系统将控制高频动力学，此时，在实际控制过程中，高增益和高穿越频率会导致低于穿越频率的未建模动力学响应，从而使得系统趋于不稳定。因此，下面利用整个系统的开环传递函数的Bode图来说明系统的稳定性。

开环系统传递函数的Bode图如下所示。

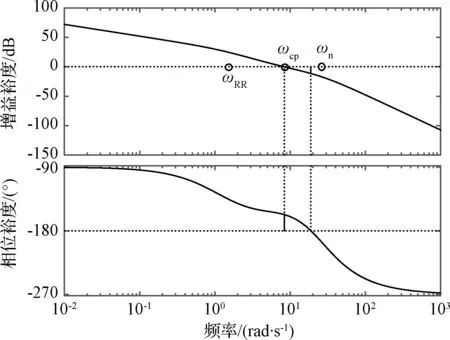
图3 开环系统传递函数Bode图Fig.3 Bode plots of open-loop system

从图3可以看出，系统的穿越频率ωcp=1.33 Hz，近似为控制器自然频率(ωn=3.98 Hz)的1/3。同时也可以看出，系统的增益裕度Gm=11.3 dB，相位裕度Pm=22.8°，因此，滚转通道的闭环控制系统具有稳定性。

为了校验滑块在实际飞行过程中的控制能力，包含滑块运动的飞行器7自由度数值仿真结果如图4～7所示。

图4 滚转角响应图Fig.4 Roll angle and roll rate vs time

图5 滑块偏移响应图Fig.5 Lateral displacement and velocity of moving mass vs time

从图4可以看出，滚转角响应在经历短暂的振荡后趋于指令值，上升时间为1.2 s，响应超调为0.39%，而滚转角速度在初始响应振荡后迅速趋于零，最大值为97 (°)/s。

从图5可以看出，对于本文所设计的总重1000 kg飞行器携带100 kg滑块的配置，在机动过程中，滑块偏移的最大距离约为0.4 m，最大偏移速度约为7.4 m/s，在实际工程中具有可实践性。滑块的偏移距离体现了执行机构的控制能力，与其质量比密切相关，这将在下文控制力矩分析中进一步分析。

图6 攻角和侧滑角响应图Fig.6 Angle of attack and sideslip angle vs time

图6为飞行器攻角和侧滑角的响应图，可以看出，滑块偏离飞行器纵轴的运动导致侧滑角的产生，但在短暂的振荡后很快衰减。攻角的偏差幅值很小，且迅速稳定到配平攻角。上述现象正是由于滑块的运动导致飞行器滚转和偏航通道产生的耦合影响。

图7为滚转通道的附加力矩的动态响应过程(为了图像清晰而省略姿态稳定后的部分)，可以看出，附加气动力矩是产生滚转角的主要因素，而附加相对惯性力矩较其他惯性力矩对滚转角的影响要大得多，在起始阶段的值与附加气动力矩相当。

3 控制力矩分析

由于滑块运动而使得飞行器受到气动外力对系统质心作用产生的附加气动力矩是变质心控制的控制力矩，根据附加气动力矩表达式，可以将其进一步改写为：

Mfa= -μBrbp×Fa=-μB(rbs0-rps0)×Fa=

-μBrbs0×Fa+μBrps0×Fa=

(36)

其中，下标s0表示滑块未偏移时系统质心的位置，因此，称-μBrbs0×Fa为附加气动稳定力矩。

式(36)表明，影响附加气动力矩的因素有滑块的纵向位置、横向位置、滑块的质量比、以及偏移量。前三者共同决定附加静稳定力矩的大小，后二者决定控制力矩的大小，其中滑块的偏移量为变质心控制的实际控制参量。

当滑块的输入指令为矩形信号时(如图8所示)，得到附加气动力矩对飞行器姿态的影响曲线，如图9所示。仿真结果表明：1)滑块运动会使得飞行攻角发生扰动，但飞行稳定攻角并不受其影响。2)在系统质心偏移的情况下气动阻力产生的力矩对飞行器偏航姿态产生一定扰动，而当滑块恢复到初始位置时该扰动也会随之消失，上述结论验证了前文理论分析的正确性。3)气动升力对系统质心偏移产生的力矩是引起飞行器滚转姿态改变的决定性因素。若没有该力矩的作用，飞行器在气动力的作用下依靠自身静稳定性以稳定滚转角飞行，与传统静稳定飞行器具有相同的性质。

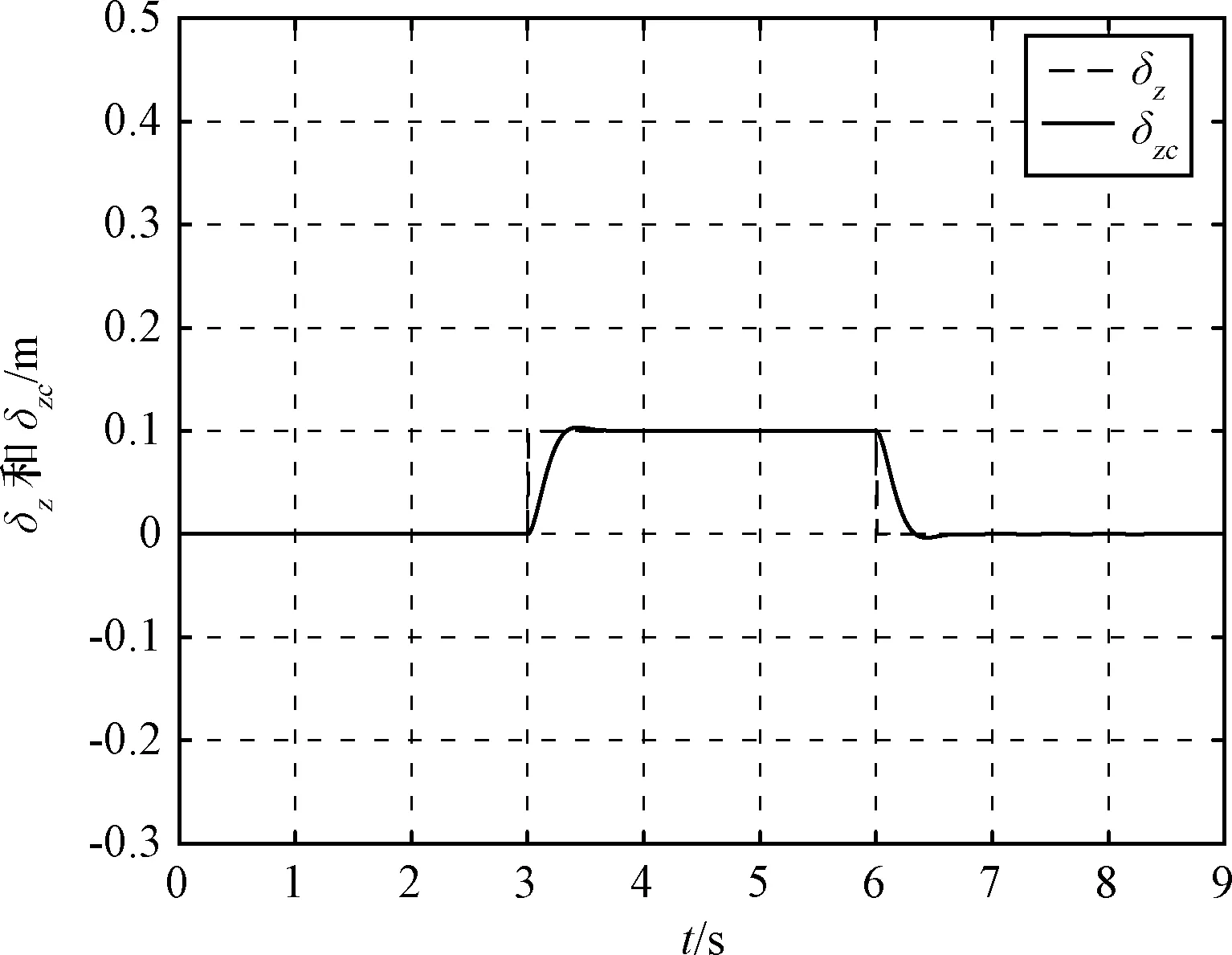
图8 滑块偏移响应图Fig.8 Lateral displacement of moving mass vs time

图9 滑块对攻角和侧滑角的影响Fig.9 Influence of additional torque from aerodynamic forces on angle of attack and sideslip angle

为了更直观地表现滑块质量比、导轨位置对附加气动力矩值的影响，在其他参数相同的情况下进行了如下仿真，结果如图10～图11所示。

图10 附加气动力矩随质量比变化曲线Fig.10 Additional torque from aerodynamic vs mass ratio

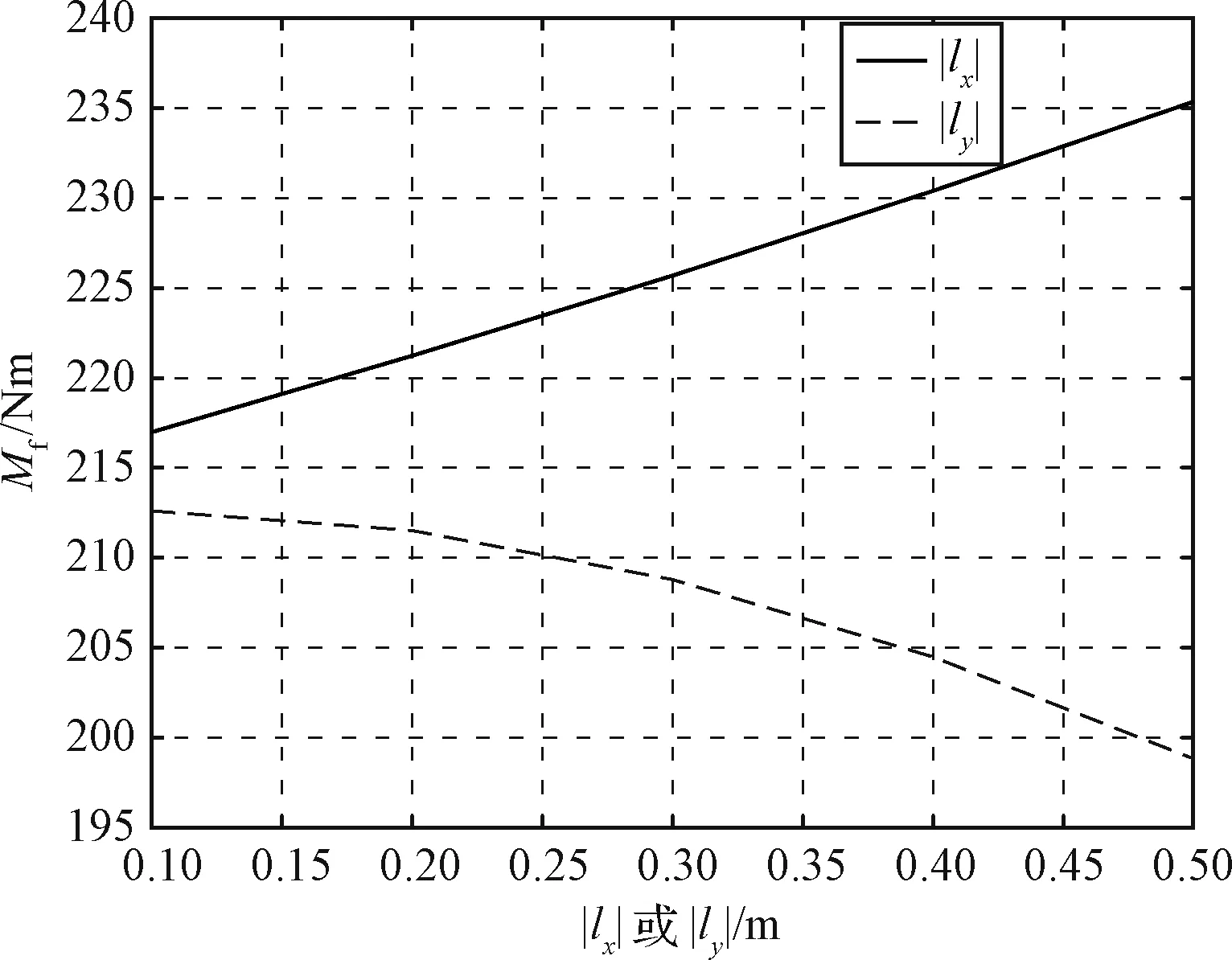
图11 附加气动力矩随导轨位置变化曲线Fig.11 Additional torque from aerodynamic vs position

图10～图11分别表示在其他参数相同而只改变滑块质量比、导轨纵向和横向位置时，飞行器受到的附加气动力矩情况。可以看出，随着滑块质量比的增大，飞行器受到的附加气动力矩也增大；当导轨纵向位置越远离载体质心，飞行器受到的附加气动力矩增大；而在载体径向方向，导轨越远离载体质心将使得附加气动力矩减小，同时也说明，这使得系统稳定性增强。综合考虑影响执行机构控制能力的各因素，导轨位置对附加气动力矩的影响相比滑块质量比的影响要小。因此，在单滑块滚控式变质心飞行器结构设计过程中，在满足载荷设计和飞行稳定性的前提下，提高其机动能力有三种途径：增大滑块质量比，增大导轨与载体质心的纵向距离，减小导轨与载体质心间的径向距离。

4 结 论

本文针对滚控式变质心飞行器，建立了包含滑块运动的七自由度完整动力学模型，并讨论了其运动特性及动力学系统特点。其次结合频域分析法对滑块运动与载体姿态运动之间的耦合影响及动态响应过程进行了详细分析，揭示了滚控式变质心飞行器的控制机理。分析结果表明，滚控式变质心飞行器可以通过较小质量比的滑块实现飞行器滚转姿态的有效控制，并且滑块运动在实现滚转控制的同时必然对偏航通道产生耦合影响，但飞行器的俯仰运动是相对独立的，只与飞行器的外形结构和执行机构位置参数有关。最后讨论了附加气动力矩对飞行器姿态控制的影响以及执行机构参数对控制能力的影响。结果表明，随着滑块质量比增大，导轨纵向位置远离飞行器质心，滑块偏移产生的控制力矩也越来越大，而导轨横向偏离质心则会导致附加气动力矩减小。因此，在单滑块滚控式变质心飞行器结构设计过程中，在满足载荷设计和飞行稳定性的前提下，提高其机动能力有三种途径：增大滑块质量比，增大导轨与载体质心的纵向距离，减小导轨与载体质心间的径向距离。本文的分析结果为滚控式变质心飞行器的工程实践提供了一些理论参考。