基于网格自适应的飞行器防热材料热传导系数辨识

章 胜，周 宇，钱炜祺，何开锋

(1. 空气动力学国家重点实验室，绵阳 621000；2. 中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000)

0 引 言

高超声速飞行器在飞行过程中会遇到复杂的气动加热现象，其对防隔热材料技术提出了严苛的要求，发展满足设计热性能要求的材料是飞行器完成既定任务的前提。气动热辨识是利用飞行器表面或防热层内部的温度测量结果来反演飞行器表面热流、防热材料热物性参数等气动热相关物理量的技术，其研究包括飞行器表面热流时间变化历程的辨识、防热材料热物性参数随温度变化规律的辨识与防热材料热源项的辨识等[1]，这些研究对促进高超声速飞行器的发展具有重要意义[2]。

气动热辨识问题又可称为热传导反演问题，其是热传导物理问题的逆问题，它在数学上的描述是针对偏微分方程系统的优化问题。近年来，国外学者在气动热辨识技术的理论研究、数值计算与实验验证等方面开展了大量深入的研究工作并在工程实际中得到了应用[3]。材料热传导系数的辨识是典型的热传导逆问题，热传导系数一般是温度的连续函数[4]，其辨识问题是无限维的约束泛函极值问题。对于此类问题，一般是通过参数化离散手段将其转化为有限维优化问题进行求解。目前，工程上材料热传导系数辨识中通常假设热传导系数为常值或随温度的变化规律确定，在此前提下进一步采用稳态法、激光法、灵敏度法等方法进行参数反演[1-3]。为了更准确地辨识热传导系数，获得其随温度的变化规律，学者们将热传导系数值按温度区间分段离散，采用折半法[5]、复变量求导法[6]、遗传算法[7]等方法辨识各温度段的数值。由于反演问题是数学上的不适定问题，当测量误差较大或反演数学模型和真实物理模型存在明显差异时，辨识结果中会出现较大的数值振荡，甚至可能出现热传导系数值小于零的违背物理实际的情况。因此，在热传导系数辨识中有必要引入相应的物理约束，从而得到更可信的结果。文献[8]在反演材料热传导系数的遗传算法基础上，考虑热传导系数值大于零、热传导系数值随温度增加而增加的物理约束，建立了热传导系数辨识方法并进行了算例考核。

从数据学习的角度讲，辨识问题也可以纳入机器学习的范畴，由统计学习理论可知：测量样本固定时，模型的复杂度越高，则模型的学习能力也越强，但过于复杂的模型通常会使得泛化性能降低[9]。对于观测数据比较有限同时噪声特性不清楚的辨识问题，研究中需要考虑在数据拟合误差与模型泛化能力之间进行折中，避免将干扰噪声误认为物理量变化规律的“过拟合”问题。另一方面，对于参数化离散得到的非线性规划问题(Non-linear programming, NLP)，不同于常用的迭代优化求解方法[10-11]，基于动态优化方程(Dynamic optimization equation, DOE)的方法是一种将NLP转化为初值问题(Initial-value problem, IVP)加以求解的方法[12-19]。虽然该类方法的研究最早可以溯源到二十世纪40年代[12]，但是其并没有得到广泛的关注，由于未知参数的寻优过程可以通过一定的动力学方程描述，其可能更适宜于在线参数辨识与控制器设计(作为增广状态)。针对考虑物理约束的高超声速飞行器防热材料热传导系数辨识问题，本文将采用多项式参数化建模技术，借鉴机器学习领域中防止“过拟合”的样本验证手段设置网格自适应调节准则，对基于DOE的优化方法在气动热辨识领域的应用进行探索，实现材料热传导系数的准确辨识。

1 材料热传导系数辨识模型

高超声速飞行器热防护层一般为多层多孔隙结构，在一定的合理假设下，防热层的三维热传导问题可以近似为一维问题进行研究[20-21]。为确定防热材料的热传导物性，工程中可对其不同方向的特性分别加以研究，确定材料热传导系数的实验原理图如图1所示，在材料上下边界为绝热边界条件的假设下，材料特定方向的传热问题可以简化为一维传热问题，当边界条件和观测条件为下述两种情形之一时，可以进行材料热传导系数的反演[8]。

1)材料内部无测点温度测量的情况：左右边界分别给定温度或热流量，将其中一个边界上除边界条件给定的状态量外的另一状态量作为观测量。

2)材料内部有测点温度测量的情况：左右边界分别给定温度或热流量，将内部测点的温度作为观测量。

图1 反演材料热传导系数的实验原理示意图Fig.1 Sketch of the experimental principle for thermal conductivity inversion

本文针对某种典型防热材料，对第二种情形下的材料热传导系数辨识进行研究，在材料左右边界给定温度边界条件，在材料内部选取一个或多个测点进行温度测量来对材料的热物性参数进行反演。材料的传热方程为

(1)

式中:T(x,t)为温度;ρ为材料密度;Cp为材料比热;k(T)为材料的热传导系数，它是温度T的函数。方程的边界条件为

(2)

初始条件为

t=0∶T(x,0)=Tt0

(3)

观测方程为

(4)

基于边界条件式(2)与初始条件式(3)，给定热传导系数k(T)，可以采用有限差分法[22]实现热传导正问题的数值求解。对于逆问题，此时热传导系数k(T)未知，需要通过观测方程式(4)中的信息对其进行辨识，在数学上该逆问题可表示为寻求k(T)使得如下性能指标达到极小

(5)

0≤k(T)

(6)

(7)

综上，热传导系数辨识问题可整理为如下约束泛函极值问题：

s.t.

x=0∶T(0,t)=Tx0

x=L∶T(L,t)=TxL

t=0∶T(x,0)=Tt0

0≤k(T)

(8)

2 辨识方法

2.1 参数化离散

参数化离散是求解形如式(8)类型的约束泛函极值问题的有效方法。所有的数值方法都是通过参数化离散手段将无穷维问题转化为有限维问题加以解决的。在众多离散方法中，基于多项式的参数化离散是一种重要的手段，其理论基础是Weierstrass于1885年提出的多项式逼近定理[23]。事实上，Weie-rstrass定理正是当前流行的求解最优控制问题的伪谱方法的理论基础[24-25]。下面首先给出该定理。

(9)

式中:上标^指代建模结果;φi(T)为Lagrange插值多项式，为

(10)

显然φi(T)满足

(11)

相应的，θi(i=1,2,…,n)的物理意义为温度Ti(i=1,2,…,n)处的热传导系数值，分析可知热传导系数模型式(9)为n-1阶多项式。

另一方面，针对物理约束式(6)和式(7)，在温度区间[Ta,Tb]取N个节点(同样T1=Ta,TN=Tb，但N≫n)，则物理约束可以表示为

(12)

采用这种方式，即使对于热传导参数物性复杂变化的情形，文中方法也易于处理。

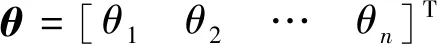
s.t.

x=0∶T(0,t)=Tx0

x=L∶T(L,t)=TxL

t=0∶T(x,0)=Tt0

0≤k(T1)

k(Tj)≤k(Tj+1)j=1,2,…,N-1

(13)

2.2 自适应网格迭代算法

为实现对未知连续变量的准确求解，数值计算中通常需要对离散网格进行加密、实施多次参数化离散以提高解的精度[26-27]。为改善热传导系数辨识结果，文中采用自适应网格迭代算法，通过调节热传导系数模型式(9)的阶次实现对真实热传导系数的逼近。热传导系数辨识问题基于对温度信号的有限含噪观测，通过使重构温度信息与真实信号间误差最小建立热传导系数辨识模型。在温度测量噪声特性未知的条件下，该误差的期望值(即期望风险)无法准确求解，根据统计学习理论中常用的经验风险最小化原则[28]，采用经验风险(文中即式(5)定义的优化指标J)作为对期望风险的估计并使之最小。但是，经验风险最小化原则是建立在测量信息足够充分的前提之下，当测量样本比较有限时(尤其是通过飞行试验获得的数据)，经验风险最小不一定代表期望风险最小，反而复杂的学习模型(在本文中，相应于多项式模型式(9)阶次增加)会导致结构风险，即模型泛化性能下降，产生“过拟合”问题。为解决这一问题，参考机器学习领域的典型做法：采用一定时域TV上的测量样本对辨识结果进行检验，定义“过拟合”检验指标

(14)

网格自适应迭代算法具体实现为：

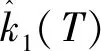
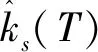
为提高计算效率，从第1次网格迭代开始，NLP问题式(13)中参数θ通过上一次的辨识结果进行初始化，即

(15)

2.3 基于DOE的NLP求解方法

针对参数化离散得到的NLP，学者们已发展了大量的求解方法，如序列二次规划方法[10]、内点方法[11]等，这些方法通过离散迭代可以对NLP进行有效求解，但它们的实现往往比较繁琐。基于DOE的优化方法是一种将NLP转化为IVP加以求解的方法，这类方法具有简洁的动力学公式表达，便于理解与使用。对于无约束的优化问题，学者们提出了梯度动力学方程[13]与连续牛顿方程[14]等DOE。为解决包含等式约束与不等式约束的一般NLP，文献[15-16]建立了求解含等式约束NLP的DOE。通过松弛参数技术，文献[17-18]将不等式约束转化为等式约束，给出了可处理不等式约束的DOE。松弛参数的引入增加了DOE的维度，对于含有大量不等式约束的问题,这会引入过多的待求参数，增加问题复杂度。文献[19]利用不等式约束的动力学特性直接对不等式约束进行处理，推导的DOE中避免了松弛参数的引入。

对于动力学优化方法得到的IVP，可以通过成熟的常微分方程积分方法进行计算，易于实现数值求解。尤其DOE对最优解的求解有理论保证，能严格保证解的全局收敛性，而且还可以得到经典最优性条件中Lagrange乘子与Karush-Kuhn-Tucker(KKT)乘子的解析表达式，直观地揭示了乘子参数与优化参数之间的理论关系[19]。

考虑一般形式的NLP，性能指标为

minJ=f(θ)

(16)

受到如下的不等式与等式约束：

g(θ)≤0

(17)

h(θ)=0

(18)

式中:θ∈Rn为待优化参数;f:Rn→R为一阶导数连续的标量函数;g:Rn→Rp、h:Rn→Rq为一阶偏导数连续的矢量函数。为建立求解NLP的DOE，文献[19]定义了如下达可行性动力学优化问题，这是一个二次规划问题，为

s.t.

(19)

式中：fθ与(gi)θ分别为函数f与gi对参数θ的梯度(列)矢量，hθ代表Jacobi矩阵，Kθ、Kh与kg分别为正定矩阵与正常数，τ为描述参数演化的虚拟时间维度，指标集Ⅱ为

Ⅱ={i|gi≥0,i=1,2,…,p}

(20)

定理2[19].对于上述定义的NLP，给定任意初始条件θτ=0，求解如下DOE

(21)

式中:Lagrange乘子参数πE∈Rq与KKT乘子参数πI∈Rp通过下式确定

(22)

(23)

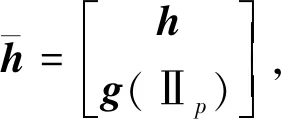
(24)

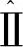
(25)

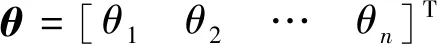
i=1,2,…,n

(26)

式(26)中需要确定温度T对θi(i=1,2,…,n)的梯度，它们可以通过求解下述灵敏度方程获得

i=1,2,…,n

(27)

相应的边界条件为

(28)

初始条件为

(29)

对于该灵敏度偏微分方程组，同样可以采用有限差分方法进行计算。对于NLP问题式(13)中的N个约束，由于热传导系数对参数θ的梯度为

(30)

基于上式，容易求得约束函数对参数θ的梯度。

3 算例分析

算例中研究的防热材料的参数为ρ=1000 kg·m-3，Cp=1000 J·kg-1·K-1，材料长为L=10 mm，左右边界的温度条件如图2中“x=0 mm”,“x=10 mm”所示，为

初始条件为

T(x,0)=600 K

测点数为m=2个，它们分别位于“x=3 mm”和“x=6 mm”位置。假设材料的热传导系数随温度的变化规律为

基于热传导方程可计算出两个测点的温度历程，图2给出了无测量噪声情况下“x=3 mm”和“x=6 mm”处的温度变化曲线。

图2 温度边界条件及测点理想温度曲线Fig.2 Temperature boundary conditions and noiseless measurement curves

3.1 无测量噪声情形

采用文中的辨识方法，第4次网格迭代后“过拟合”检验指标增加，因此最终辨识热传导系数采用第3次网格迭代后的计算结果，表1给出了网格迭代过程中的具体结果，从表1中可以看到，最终辨识的热传导系数对应的优化与检验指标值均很小，这说明其与真实值很接近。

表1 无测量噪声情形的辨识结果Table 1 Identified results without measurement noise

图3给出了初始网格下NLP参数动力学发展曲线，可以看到在设置的Kθ下参数收敛很快，在τ=1 s时结果已趋于稳定，这说明了本文发展的DOE的高效性。图4给出了第4次迭代网格下NLP参数辨识的过程曲线，最终结果与初始值几乎完全相同，表明文中基于上一步辨识结果设置参数初值的方式可以提供良好的初始值。根据表1的辨识结果，图5给出了初始网格下得到的热传导系数、最终辨识的热传导系数与真实系数的比较曲线，可以看到辨识结果很好地满足了实际物理约束，但线性近似与真实曲线之间还是存在较明显的差异，而最终辨识结果与真实曲线几乎完全重合，最大误差仅为3.5020×10-5W·m-1·K-1。

图3 无测量噪声情形初始网格参数辨识曲线Fig.3 Identification curve for the parameters of the initial mesh without measurement noise

图4 无测量噪声情形第4次迭代网格参数辨识曲线Fig.4 Identification curve for the parameters of the 4th refined mesh without measurement noise

图5 无测量噪声情形辨识热传导系数与真实系数比较Fig.5 Comparison between the identified thermal conductivity without measurement noise and the true quantity

3.2 含测量噪声情形

进一步考虑测量中存在噪声的情形，假设噪声服从正态分布，均值为0，标准差为σ=4 K，辨识计算条件与无噪声情形完全相同。表2给出了热传导系数辨识过程中的具体计算结果，其中第2次网格迭代后的结果对应的“过拟合”检验指标最小，说明此时达到了“经验风险”与“结构风险”的最佳折中。注意不同于无测量噪声情形，由于噪声的影响，辨识结果对应的指标值并不接近于0值。

图6给出了辨识的热传导系数与真实系数的比较曲线，从图中看到存在噪声时候辨识结果与真实曲线之间有一定的细微差别(最大误差为0.0165 W·m-1·K-1)，但是其仍然很好地反映了真实物理量的变化规律。为进行比较，图7给出了第3次迭代网格下的辨识结果，表2中的检验指标显示此时结果出现了“过拟合”现象，从图中也看到辨识的热传导系数与真值间的误差开始增大(最大误差为0.0744 W·m-1·K-1)。通过对比，表明本文自适应网格迭代算法“学习”到了更接近于真实物理量的结果。图8给出了基于辨识的热传导系数重构的温度状态与测量量的对比结果，可以看到重构结果较好地拟合了测量信息。

表2 含测量噪声情形的辨识结果Table 2 Identified results with measurement noise

图6 有测量噪声情形辨识热传导系数与真实系数比较Fig.6 Comparison between the identified thermal conductivity with measurement noise and the true quantity

图7 有测量噪声情形“过拟合”热传导系数与真实系数比较Fig.7 Comparison between the over-fitted thermal conductivity with measurement noise and the true quantity

图8 温度测量结果与重构曲线比较Fig.8 Comparison between the temperature measurement and the reconstructed results

4 结 论

考虑物理约束的高超声速飞行器防热材料热传导系数辨识是针对偏微分方程系统的约束泛函极值问题，本文对该问题进行了有效求解，辨识结果较准确地反映了热传导系数的变化规律。研究表明本文采用的多项式建模手段可以较好地模拟材料热传导系数的物理特性，发展的动态优化方程能有效求解最优参数，对于测量数据比较有限的问题，借鉴“机器学习”思想，提出的基于“过拟合”指标的网格自适应迭代方法能实现模型准确性与泛化性能的较好折中。

由于热传导系数的模型结构是通过“学习”确定，本文方法相较于之前确定模型结构的辨识方法更具灵活性。基于动态优化方程的非线性规划方法在工程上的应用较新颖，本文工作也证明了这种方法的有效性。在本文中，三维传热问题是简化为一维问题加以求解，为更准确地获得材料的热传导物性，下一步将针对多维情形的问题开展研究。