定位方案三维稳健性分析及一般解推导
林 嘉, 杨夫勇, 郑 丞, 金 隼
(1. 上海交通大学 上海市复杂薄板结构数字化制造重点实验室, 上海 200240;2. 上海飞机制造有限公司 制造工程部, 上海 200436)
几何精度对机械产品的外观、性能及其生产效率都有直接的影响, 是衡量产品制造质量的一个重要指标. 作为工件加工、装配和测量过程的基本环节, 定位过程产生的误差是最终产品几何误差的一个重要来源, 其主要受到2类因素的影响: ① 零部件及工装夹具上定位基准的制造误差等上游因素; ② 定位方案等工艺因素. 通过对定位方案的稳健设计, 降低定位误差对定位基准制造误差的敏感度, 是提高工件定位精度并最终提高产品制造质量的一种重要手段.
围绕定位方案稳健设计, 国内外的学者开展了大量的研究. 从刚性零件定位约束的运动学分析入手, 文献[1-3]中研究了零件的确定性定位和完全约束. 文献[4-5]中建立了夹具定位点和零件的接触约束方程, 在此基础上采用线性微分法建立了三维工件定位误差分析模型, 为空间三维定位方案的稳健设计奠定了基础. 在稳健定位方案求解方面, Cai等[4]采用非线性规划的方法求解三维工件的稳健定位方案; Wang[6]采用试验设计的方法对定位方案进行了比较和优选; Huang等[7]提出了一种可变顺序空间填充算法来搜索定位方案的最优解. 针对工件定位的稳定性, 姜昂等[8]采用遗传算法搜索最佳定位点; Wang等[9]将稳健性和稳定性同时作为定位方案的优化目标, 比较了遗传算法和蚁群算法求解多目标优化问题的效果. 针对多工位装配的定位方案稳健设计, Tian等[10]采用遗传算法进行求解; Vasundara等[11]提出了一种结合遗传算法和汉默斯里序列抽样的2步优化策略; Tyagi等[12]提出了一种基于局部增量算法的启发式优化算法. 由于三维定位误差分析模型参数众多、形式复杂, 所以上述研究多采用数值的方法搜索求解稳健方案. 数值方法的局限性在于只能获得各设计参数以具体的数值形式表示的特解, 而无法获得以各参数相互关系式表示的一般解, 因此难以直观严格地揭示共性规律.
本文针对三维空间定位, 结合常用的工程条件和习惯, 在引入2个附加假设对三维定位误差分析模型进行简化的基础上, 对定位方案的稳健性进行解析分析并求解其优化设计的一般解, 以揭示其中的共性规律, 供设计人员参考.
1 三维定位误差分析模型及其简化
针对三维工件的6点确定性定位, 在刚性及小位移假设下, 推导了定位误差与定位参数(6个定位点的位置坐标、控制方向)及定位点制造误差之间的定量关系[4]:

式(1)是一个通用模型, 参数众多,形式复杂, 很难进行解析上的分析.本文结合常用的工程条件和习惯, 引入2个附加假设对其进行简化.
假设1定位点垂直于其控制方向的制造误差可忽略.
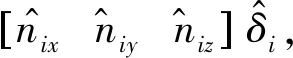
[δxiδyiδzi]=
(2)

(3)
(4)
把式(2)~(4)代入式(1), 可得
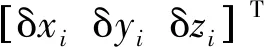

(5)
可见, 垂直于控制方向的误差对测点误差的影响可以忽略. 式(1)可简化为
(6)

图1 定位点制造误差的分解Fig.1 Decomposition of the geometric error at a locator
这一现象的产生是由于在推导式(1)的过程中, 在小位移假设的基础上以工件在定位点处的切平面来表征工件在该处的实际表面[4], 假设1实质上是小位移假设的一个延伸.
假设2定位点控制方向与坐标轴方向平行.
为了降低定位点设置不当带来的影响, 在工程中定位点的控制方向往往设计成与全局或工件坐标系的坐标网格(轴)平行或近似平行[13], 如图2所示. 这在汽车制造业中称之为网格平行性准则[13], 本文将该条件作为第2个假设引入.

图2 控制方向平行于坐标轴的定位点Fig.2 Locators with control parallel to the axes of coordinate system
不失一般性地, 假设第1定位方向为z向, 第2定位方向为y向, 第3定位方向为x向. 在本文的后续推导中将沿用此假设. 6个定位点的控制方向具体为
(7)
把式(7)代入式(6), 最终可得
(8)
式(8)相对式(1)形式大为简化, 设计参数亦由36个减少至12个, 使解析分析和求解成为可能.
2 定位方案稳健性分析及优化设计
对简化后的Jacobian矩阵求逆, 由式(8)可得
(9)
式中:
2.1 定位方案稳健性的影响因素
由式(9)可知, 工件的定位误差由定位点的位置以及定位点的制造误差共同决定, 其中定位点的位置决定了定位方案的稳健性. 根据式(9)的具体形式, 可以得出以下结论:
(1) 在遵循网格平行性准则的情况下, 各个定位点沿其控制方向的位置对工件定位误差没有影响. 即式(9)中没有出现的z1、z2、z3、y4、y5和x6不影响定位方案的稳健性.
图3所示为沿控制方向定位点的位置变动, 实线定位点和虚线定位点分别表示2套不同的定位方案. 这2套方案的定位点位置只在沿其控制方向上存在差异, 而稳健性则完全相同.
(2) 控制第1定位方向的3个定位点, 沿其控制方向的投影三角形面积不能为0; 控制第2定位方向的2个定位点, 沿第3定位方向的坐标不能相等. 即
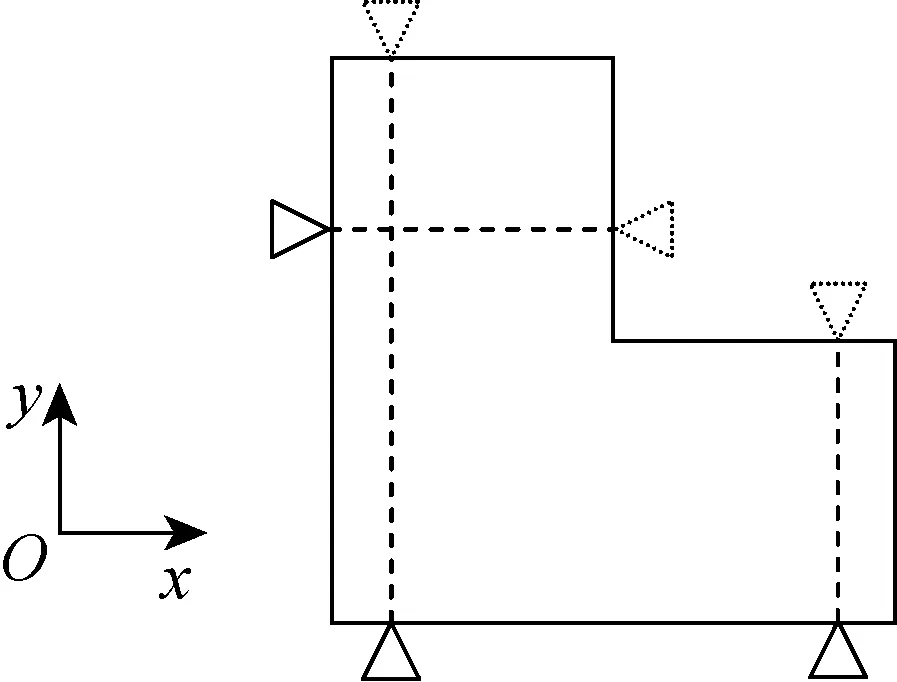
图3 沿控制方向的定位点位置变动Fig.3 Positional variation of locators along their controlling directions
(x4-x5)(y2x1+y3x2+y1x3-
y1x2-y2x3-y3x1)≠0
(10)
(3) 工件沿第1定位方向的定位误差只与控制该方向的3个定位点的位置和制造误差有关; 沿第2定位方向的定位误差只与控制第1、第2定位方向的5个定位点的位置和制造误差有关; 沿第3定位方向的定位误差与所有6个定位点的位置和制造误差都有关.
(4) 特别地, 对于平板工件, 由于工件本身形状的特点, 6个定位点沿第1定位方向的坐标满足
z1=…=z6=z
(11)
把式(11)代入式(9), 可得
(12)
观察式(12)中的传递矩阵可知, 此时矩阵的第1~3列只与控制第1定位方向的3个定位点的位置有关, 矩阵的第4~6列只与控制第2、第3定位方向的另外3个定位点位置有关. 2组定位点之间不存在对定位误差的交互作用, 其布置优化可分别进行.
2.2 定位方案稳健设计的一般解
本文仅针对单测点的情况, 稳健设计的目标为位于坐标系原点的测点沿3个坐标轴方向定位误差的波动总和最小.某最稳健定位方案如图4所示.

图4 某最稳健定位方案Fig.4 A most robust locating scheme
假设6个定位点具有相同的制造精度, 沿其控制方向制造误差的方差D(δi)=σ2, 由式(9)可得
D=D(δx0)+D(δy0)+D(δz0)=
(13)
式中:
ε2=y3x2-y2x3
ε3=y1x3-y3x1
ε4=y2x1-y1x2
(1) 由式(9)和(13)可知, 控制第3定位方向的定位点6, 其坐标y6和z6仅对D(δx0)有影响. 对
(14)

f1y6+f2z6=0,f3z6+f4y6=0
(15)
式中:
f1,f2,f3和f4是与y6和z6无关的函数, 且f1f3≠f2f4, 为保证式(15)成立需满足
y6=0,z6=0
(16)
式(16)的物理含义为, 控制第3定位方向的1个定位点, 沿该方向的投影与测点重合, 如图4中的C1点. 将式(16)代入式(14), 等号成立; 将式(16)代入式(9), 第1行的前5个元素为0. 此时, 测点沿该第3定位方向的定位误差仅与控制该方向的1个定位点有关, 并且其方差D(δx0)取得最小值σ2.
(2) 当式(16)满足时, 由式(9)和(13)可知, 控制第2定位方向的定位点4和5, 其坐标x4、z4、x5和z5仅对D(δy0)有影响. 对
(17)
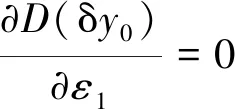
f5ε1=0
(18)
式中:
f5为与变量ε1无关的函数, 为保证式(18)成立,需满足
ε1=z4x5-z5x4=0
(19)
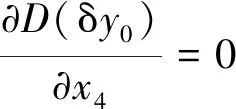
(20)
联立式(20)中的2个方程并结合式(10), 可得
(21)
进一步可得
x4+x5=0
(22)
式(19)和(22)的物理含义为, 控制第2定位方向的2个定位点, 沿该方向投影线段的中点与测点重合, 如图4中B1和B2点. 把式(19)和(22)代入式(17), 等号成立; 把式(19)代入式(9), 第2行的前3个元素为0. 此时, 测点沿第2定位方向的定位误差仅与控制该方向的2个定位点有关, 且其方差D(δy0)取得最小值σ2/2.
(3) 当式(16)、(19)和(22)满足时, 由式(9)和(13)可知, 控制第1定位方向的定位点1、2、3, 其坐标x1、y1、x2、y2、x3、y3仅对D(δz0)有影响,
在手机应用、互联网服务器以及运营商核心网引入网络状态数据的收集、模型运算以及QoS调用的准入功能,能有效确保用户感知指标,有利于运营商能力开放业务的顺利开展。本文成果主要以手机游戏为应用对象,在移动互联网中不同
(23)
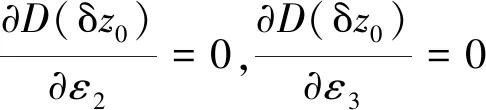
(24)
联立式(24)中的3个方程并结合式(10)可得
(25)
进一步可得
ε2=ε3=ε4
(26)
将式(26)代入式(23), 等号成立. 由ε2,ε3,ε4的表达式以及式(26)可得
(27)
式(27)的物理含义为, 控制第1定位方向的3个定位点, 沿该方向的投影三角形的形心与测点重合, 如图4中的A1、A2和A3点. 此时, 测点沿第1定位方向定位误差的方差D(δz0)取得最小值σ2/3.
需要注意的是, 同时满足式(16)、(19)、(22)和(27)的最稳健定位方案有无数种, 而图4中所示的方案只是其中的一种.
3 算例
3.1 某平板工件定位方案比较及VisVSA分析验证
VisVSA是工程中常用的主流商用3维偏差分析软件之一, 其算法以Monte Carlo模拟为基础, 在抽样次数较高的情况下具有很高的收敛精度. 由3定位块+1四向销+1二向销构成的一面两销定位是最经典的定位方式之一, 同时在分析中也易于转化为6点定位的形式. 本文以采用该定位方式的某平板工件为例, 针对多种定位布置方案, 分别根据前文分析推导得到的结论以及商用3维偏差分析软件VisVSA的定量分析结果, 对其稳健性进行比较, 以验证前文结论的准确性.
该平板工件及其定位方案如图5所示. 坐标系原点设在测点处, 垂直纸面方向为z向; 在分析中, 二向销和四向销分别转化为控制其短轴方向和2个相互垂直方向的定位点, 不考虑孔销配合间隙; 各定位点的制造误差皆服从正态分布N(0, 1). 其中:方案1是根据2.2节的分析结论布置的最优定位方案;方案2在方案1的基础上, 将二向销的位置沿其控制方向进行了平移. 根据2.1节的分析结论, 定位点沿其控制方向的位置变动对定位精度无影响, 其定位精度应与方案1一致.

图5 某平板工件的4种定位方案Fig.5 4 different locating schemes of a plate workpiece
方案4在方案3的基础上, 对3个定位块的位置进行了调整, 使投影三角形的形心偏离测点. 根据2.2节的分析结论, 测点沿第1定位方向即z向的定位精度将降低.
利用VisVSA计算这4种方案下的定位精度, Monte Carlo模拟抽样次数为 5 000 次, 结果如表1

表1 各方案VisVSA及本文方法定位精度分析结果Tab.1 Analyzed geometric variations from VisVSA and the proposed method under different locating schemes
所示. 此外, 表1中同时列出了直接结合式(9)和统计法得到的计算结果.
由表1可见:VisVSA对各方案定位精度的比较结果与本文的比较结果完全吻合;结合式(9)和统计法得到的定量分析结果与VisVSA的定量分析结果也非常接近.
3.2 某飞机后机身冲压排气管安装定位方案优化
利用前文分析推导的结论对某飞机后机身冲压排气管的安装定位方案进行优化. 该冲压排气管与上游管道采用软管进行连接, 配合精度要求不高. 安装过程存在的主要风险是安装到蒙皮后因误差过大而导致的与其前侧斜框的间距过小, 这将可能在飞机飞行过程中由于晃动而发生干涉.
当前冲压排气管的安装定位方案如图6所示. 第1基准为法兰面A, 第2基准为法兰面上的定位孔B0, 第3基准为开口中心人工对齐点C0. 以下对其进行优化: 由于结构限制, 其第1基准难以更改; 而根据 2.2 节的分析结论, 应选择可能干涉方向作为第2定位方向以加强对该方向定位精度的控制, 且控制该方向的2个定位点的布置使得可能干涉位置沿该方向的投影尽量靠近两定位点的中点. 优化后的第2、第3基准为图6中的B、C点, 分别为法兰面上的2个定位孔.

图6 某飞机后机身冲压排气管Fig.6 A stamp exhaust pipe at the rear fuselage
为了验证优化效果, 利用VisVSA分别对2种方案进行装配精度分析. 主要模拟参数: 后机身包括蒙皮和斜框加强件作为基件, 冲压排气管作为被安装件; 各零件相关关键特征的公差如表2所示.表中: 蒙皮和斜框加强件的公差为其在后机身部件状态下的公差; 可能干涉位置的配合间距要求不小于4 mm; Monte Carlo模拟抽样次数为 5 000 次. 另外, 为了使定位方案本身更具可比性, 在原方案的模拟中将开口中心人工对齐点的位置度公差参照定位孔亦分别设置为1和 0.5 mm.
在VisVSA中建立的模型及其分析结果如表3所示. 在对其他参数不作调整, 仅对第2、第3基准的位置进行优化的情况下, 两处可能干涉位置配合间距的超差率和标准差都有所降低.
表2 各零件关键特征公差
Tab.2 Assigned tolerances on the key characteristics of the mating parts

零部件关键特征制造公差/mm蒙皮 内形面轮廓度5排气管定位孔位置度1开口中心人工对齐点位置度2斜框加强件外表面轮廓度2法兰面轮廓度1冲压排气管定位孔位置度0.5开口中心人工对齐点位置度1排气管外表面轮廓度1

表3 VisVSA装配精度分析结果Tab.3 Analyzed assembly variations from VisVSA
4 结语
现有关于三维定位方案稳健设计的研究多使用数值方法进行求解. 数值解法适应性强, 而解析分析及通过解析分析获得的一般解能更直观严格地揭示共性规律. 本文结合常用的工程条件和习惯引入2个附加假设, 在对三维确定性定位误差分析模型进行简化的基础上, 用解析的方法分析了定位方案稳健性的影响因素, 并针对单测点的定位误差控制, 求解了定位点最稳健布置的一般解.此外,得到了以下一些三维工件空间定位方案稳健设计的一般规律:
(1) 在遵循网格平行性准则的情况下, 各定位点沿其控制方向在何处布置对定位精度没有影响;
(2) 定位点沿其他2个方向的最佳位置, 应使得控制同一方向的各定位点沿该方向的几何投影形心与测点重合;
(3) 在满足规律(2)且假定各定位点制造精度相同的情况下, 测点沿第1定位方向的定位精度最高, 第2定位方向次之, 第3定位方向最低, 其比例关系为1/3∶1/2∶1.
掌握这些规律可以帮助工程技术人员理解、评估设计方案的影响, 从而设计出更为稳健的定位方案.

