基于稳定性分析的电控离合器任务调度周期设计

程小宣, 陈 俐

(上海交通大学 海洋工程国家重点实验室；高新船舶与深海开发装备协同创新中心， 上海 200240)

电控离合器是重要的传动控制部件[1]，在汽车液力式自动变速器[2]、自动机械式变速器[3]、双离合自动变速器[4]、无级变速器[5]以及混合动力耦合装置[6]中应用广泛.电控离合器的接合过程控制不当可能引起传动系统剧烈冲击以及摩擦片过度磨损，降低整车行驶平顺性以及传动部件使用寿命.在实际工程中，离合器控制算法被编译并运行在车载嵌入式控制器中，该控制器需要处理包括离合器控制在内的一些任务.受成本、体积与功耗等的限制，嵌入式控制器需要合理设计每个任务的调度周期，即综合考虑控制性能和计算机资源，以期在满足离合器接合品质要求的前提下，降低控制器的成本.对于离合器控制而言，短时间内(一般在1 s左右[7])接合过程经历3个阶段，即空行程、滑摩阶段和锁止阶段，而且滑摩阶段与空行程和锁止阶段的动力学方程并不连续，因此，嵌入式控制器的离散化带来的信号不平滑对该过程可能产生复杂影响，有必要进行系统分析，为离合器控制算法的任务调度周期提供设计依据.

离合器接合过程的性能评价指标主要为整车冲击度和摩擦片滑摩功损失，为了提升接合品质，国内外学者深入研究了接合过程前馈与反馈控制策略，如基于平坦度并结合线性反馈设计的非线性前馈算法[8]；利用PI控制使实际转速差跟随理想预设轨迹[9]；非线性前馈-反馈控制算法[10]；以及多种最优控制算法，包括状态观测器算法[11]、线性二次型最优控制(LQR)[12]和模型预测控制(MPC)[13]等.但是以往的控制策略都在连续域内进行设计，未考虑离散后任务调度周期的影响.

另一方面，随着多任务计算机与嵌入式控制器的广泛应用，实时任务调度周期的设计备受关注[14-19].在时间和资源受限的嵌入式系统中，Wu 等[15]通过选取合适的任务调度周期，提高系统的控制性能；Aydin等[16]针对基于奖励所执行任务的调度问题，提出了成本函数的解决方案；为解决噪声强度和控制回路中的计算延迟，Cervin等[17]调整了不同的计算周期.还有大量工作集中于在线工作量、网络问题等[18-19]对实时任务调度周期选取和优化的影响.由于网络控制系统中各组件之间的通信能力有限，Dai等[18]通过确定实时调度策略，实现了控制回路的稳定性；Zhang等[19]进一步集中于网络控制系统中存在的时间延迟、传输间隔、数据量化等问题，优化系统性能.但是上述研究均将控制任务简化为计算负荷，无法反映任务调度周期对控制性能的影响.

针对离合器接合过程的实时控制问题，本文基于控制性能和实时调度协同设计的思路，提出根据控制系统的动态性能设计任务调度周期.首先建立离合器接合过程的动力学模型和闭环反馈控制策略模型，对该控制系统进行离散化，在离散域中开展稳定性分析，并依据系统动态性能评价离合器接合品质.基于系统稳定性和接合品质选择任务调度周期，在MATLAB/Simulink仿真环境中和传动台架上进行不同任务调度周期对离合器接合品质影响的试验.

1 系统建模

图1 离合器闭环控制系统模型Fig.1 Diagram of closed-loop control system during clutch engagement

1.1 动力传动子系统

动力传动子系统的简化模型如图2所示，包括发动机端、离合器、整车端以及相应的弹性元件[20].其中：Je为发动机端转动惯量；Jc1为离合器主动端的转动惯量；Jc2为离合器从动端转动惯量；Jv为离合器输出轴后的等效惯性惯量；ke,kv代表两端刚度；ce,cv为阻尼系数；Te为发动机的输出转矩；Tc为离合器转矩；Tv为车辆负载转矩.

由图2得到4自由度动力学方程如下:

(1)

(2)

(3)

(4)

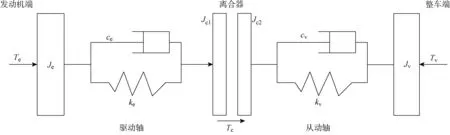
图2 动力传动系统模型Fig.2 Powertrain model

式中：θe,θc1,θc2,θv分别代表发动机端、离合器主动轴、从动轴和整车端的输出角位移.

其中式(1)和(2)描述发动机端动力学，式(3)和(4)描述整车端动力学.

由离合器状态定义离合器输出转矩，其表达式为

(5)

(6)

由式(5)可知，在空行程中离合器转矩Tc为0；Tc仅在滑摩阶段是可控的，由Fn决定；而在锁止阶段Tc为一段范围内的任意值，该范围边界也由Fn决定.因此Fn连接了离合器接合过程的3个阶段，对离合器接合性能影响很大.

车辆输入负载转矩Tv按下式计算[21-22]：

Tv=(Fair+Fr+Ft)R

(7)

式中：R为轮胎半径；Fair,Fr,Ft分别为风阻、坡道阻力和轮胎滚动摩擦阻力，

0.5cDAVρair(νair+v)2

(8)

Fr=mgsinα

(9)

Ft=fmgcosα

(10)

式中：cD为气动阻力系数；AV为汽车迎风面积；ρair为空气密度；vair为迎面风速；v为汽车速度；m为汽车质量；g为重力加速度；α为坡道角度；f为轮胎摩擦系数.

输出轴角速度和车速的关系如下(其中iv为齿速比)：

(11)

1.2 反馈控制子系统

在离合器控制中，反馈闭环应用普遍[23-25].本文采用理想工况下可获得理想输出的比例反馈控制算法：

(12)

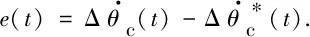
将式(12)进行拉普拉斯变换，得到含复变量s反馈控制传递函数：

Hfb(s)=Kp

(13)

1.3 执行延迟子系统

Hd(s)=e-τs

(14)

1.4 零阶保持器子系统

(15)

k=0,1,…,n

零阶保持器环节的传递函数为

(16)

2 系统稳定性分析

由式(1)～(4)可以得知，整车端与发动机端的动力学分析相似.两端均描述了包含刚度和阻尼系数的2自由度运动；同时，两端方程的状态变量各自独立，因此整车端与发动机端的稳定性分析过程一致.下文提供了整车端的动力学推导，其方法可以通过改变参数运用到对发动机端的分析中.本节首先推导出图1中各子系统在连续时间域内的传递函数；接着对其做z变换进行离散化；然后通过计算z域的特征根分布分析不同任务调度周期下的系统稳定性，确定在稳定性条件限制下的临界任务调度周期.

2.1 系统离散化

Hp(s)=

其他3个子系统的传递函数表达式已由式(13)，(14)和(16)获得，则系统开环传递函数为

H(s)=Hfb(s)Hz(s)Hd(s)Hp(s)

(17)

相应闭环传递函数为

(18)

进行z变换后，得到：

(19)

闭环控制系统的特征方程为

1+H(z)=0

(20)

在式(19)和(20)中，任务调度周期T没有具体数值；下面一节对T进行赋值分析，求出式(20)的特征根.

2.2 特征根分析

假设T=0.1 s和T=0.2 s，求出对应的特征根.接着绘制出随任务调度周期T变化的特征根轨迹图，分析参数如表1所述.

首先令T=0.1 s，代入式(17)并进行z变换后，得到开环传递函数：

表1 稳定性分析参数表Tab.1 Parameters for stability analysis

H(z)=(1.035z5+0.475 1z4-0.093 95z3+

0.148 4z2-0.044 45z+0.004 26)/

(z6-0.740 2z5-0.239 5z4-

0.020 14z3-1.462×10-4z2-

3.736×10-7z)

(21)

根据式(20)求出对应的6项特征根为

z1=-0.512+0.571i

z2=-0.512-0.571i

z3=0.164+0.067i

z4=0.164-0.067i

z5=0.200+0.436i

z6=0.200-0.436i

由结果可知，特征根都分布在z域的单位圆内.根据数字控制系统的稳定性标准[26]，闭环系统稳定.

令T=0.2 s，推导得到开环传递函数：

H(z)=(2.649z5+0.964 2z4+0.131 9z3+

0.008 846z2+7.676×10-4z+

2.604×10-6)/(z6-0.740 2z5-

0.239 5z4-0.020 14z3-

1.462×10-4z2-3.736×10-7z)

(22)

根据式(20)求出对应的6项特征根为

z1=-1.463

z2=-0.003

z3=-0.209+0.086i

z4=-0.209-0.086i

z5=-0.012+0.098i

z6=-0.012-0.098i

其中最大特征根分布在z域的单位圆之外，此时闭环系统不稳定.

接着在0.001 s ≤T≤0.2 s之内，每隔0.001 s计算出对应传递函数的特征根，并绘出根轨迹图，如图3所示.横坐标为任务调度周期T，纵坐标为6项特征根的模的最大值.由图可知，当T<0.15 s 时，最大特征根的模小于1.因此当调度周期小于0.15 s 时，闭环系统稳定，即本节求得临界任务调度周期Tmax为0.15 s.

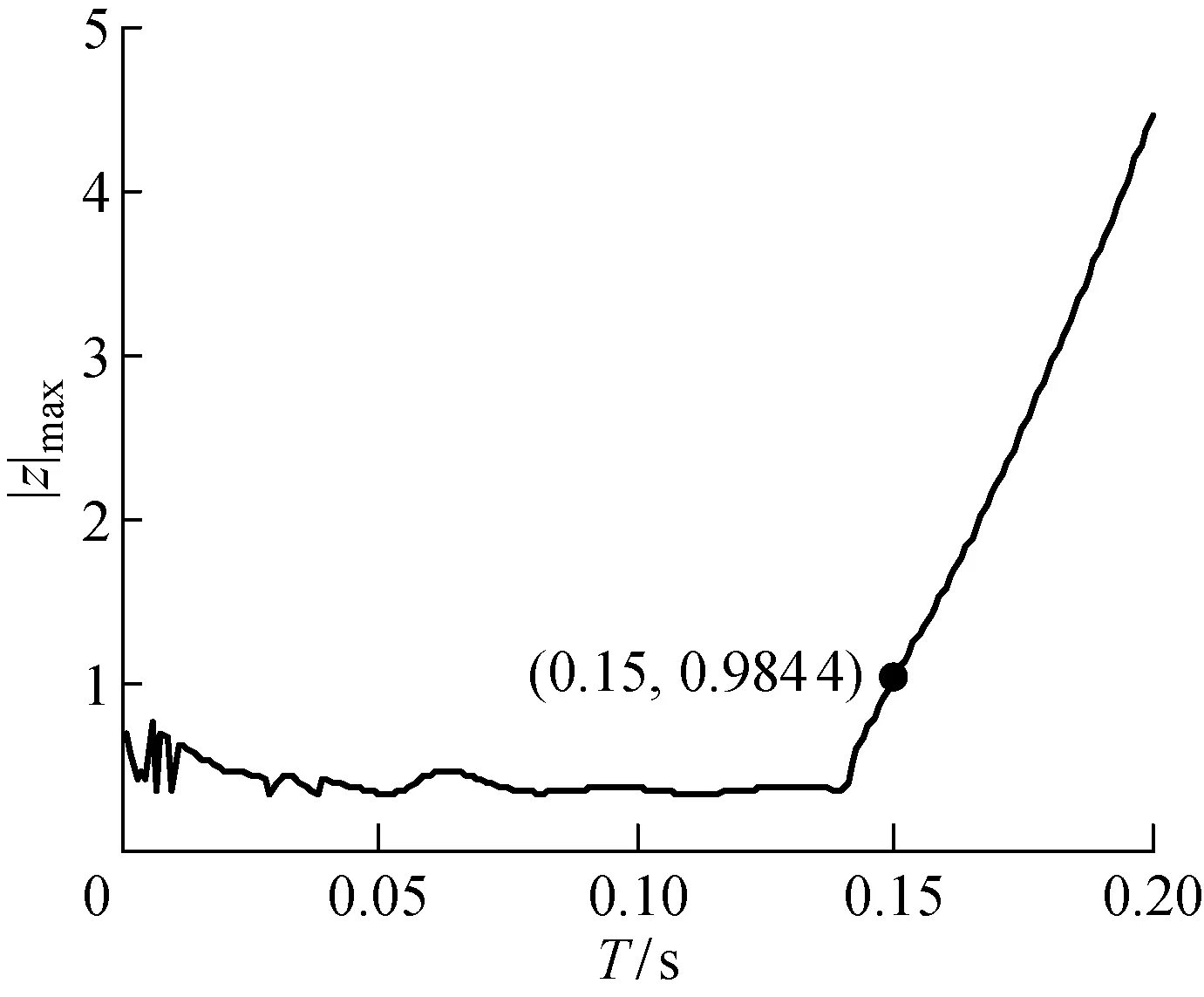
图3 随任务调度周期变化的最大特征根趋势图Fig.3 Maximum module of the characteristic roots variation with task period T

3 仿真结果分析

上文选取了系统稳定时的临界任务调度周期，但是稳定性条件是限制任务调度周期的极限边界，处于该边界范围内并不能保证离合器获得较好的接合控制性能.因此，本节利用MATLAB/Simulink仿真环境，分析不同的任务调度周期对离合器接合品质的影响，具体的参数如表1以及表2所示.图4所示是不同的任务调度周期下离合器接合过程的动态响应.

表2 仿真参数表Tab.2 Parameters for simulation

离合器的接合品质由整车冲击度和滑摩功损失评估，冲击度j描述车辆行驶的平顺性，是车辆加速度的导数；滑摩功损失ED是离合器滑摩过程中能量的损失大小，它的计算公式为

(26)

图4中的工况1为任务调度周期T=0时的连续系统响应，作为比较基准图，可知离合器传递扭矩Tc平稳增加；主动端和从动端的转速能够平顺接合，并且在起步阶段和接合完成时的整车冲击度很小.

不改变其他参数，工况2中令T=0.01 s，滑摩初始阶段出现振颤现象，导致离合器传递扭矩产生超调；离合器主动端和从动端的转速在滑动一段时间后能够接合，但是相比工况1，此时滑摩阶段和锁止阶段的整车冲击度明显增大.

当T=0.1 s时，如工况3所示，Tc由于零阶保持器中任务调度周期的作用，呈现明显的阶梯状；虽然离合器主、从动端转速仍能够接合，但是传递扭矩的波动导致整车冲击度增长了数万倍，将会对车辆动力传动系统造成很大破坏；由于离合器主动端转速的剧烈变化，滑摩功损失大小增加到工况1的3倍.此时在系统稳定性方面，任务调度周期已接近图3中得到的临界任务调度周期.

任务调度周期T=0.15 s时的离合器接合动态响应过程如工况4所示.此时离合器接合过程的闭环系统刚进入不稳定区域，离合器扭矩的震颤导致冲击度达到了105数量级，在破坏传动系统部件的同时会极大降低驾驶舒适性.且离合器主动端转速在滑摩阶段有增大趋势，无法平顺地接合，此时滑摩功大小增加至工况1的5倍.

工况5中当T=0.2 s时，已超过临界任务调度周期，动态响应结果更为恶劣，离合器转矩存在较大振颤，冲击度增大至工况4的2倍，滑摩功损失约为工况1中的8倍，基本呈现几何倍数增长的趋势；并且在锁止阶段，离合器传递扭矩和整车冲击度的剧烈波动仍无法抑止，此时滑摩功损失呈现逐渐增大的趋势.

本节选取任务调度周期范围为0.001 s0.15 s时，整车冲击度会剧烈增大，即为系统稳定与不稳定的分界点.特别地，当T<0.011 s时，冲击度可以维持在理想范围10 m/s3之内.

图4 不同任务调度周期的系统动态响应Fig.4 Dynamic responses under different task scheduling periods

图5 随任务调度周期变化的最大冲击度趋势图Fig.5 Maximum vehicle jerk variation with task schedul- ing period

4 台架试验结果分析

本文在传动试验台架上进行试验验证，双离合变速器DCT250被安装在驱动和负载测功机之间，如图6所示.作为DCT250关键部件的离合器控制信号由dSPACE实时仿真系统通过CAN总线传输到变速箱控制单元中.其中传感器的信号如驱动和负载测功机的转矩、转速等，都是由ETAS系统进行数据采集.

在台架试验中测试了3种工况，结果如图7所示.工况1中T=0.01 s，离合器传递扭矩迅速增大随后缓慢减小，离合器主动端和从动端的转速在滑动一段时间后能够顺利接合，整车冲击度和滑摩功损失的大小相对较小.

工况2中T=0.1 s，已接近第2节中分析得到的临界任务调度周期0.15 s，此时离合器传递扭矩和工况1中的扭矩相近，但是在接合完成阶段出现了一个回升波动，整车冲击度也有所增加，由工况2可知，此时最大冲击度为43 m·s-3，相比工况1增大了38%；离合器主动端转速在起步加速阶段的时间小于工况1中的时间，接合趋于同步阶段的主动端转速变化增大，导致滑摩功损失的大小达到工况1中的2倍.

当任务调度周期变为工况3中的T=0.2 s时，即超出临界任务调度周期，系统出现了明显振颤现象.离合器传递扭矩和整车冲击度发生剧烈波动，整车冲击度的最大值为96 m·s-3，增大至工况1的3倍，远远超过了冲击度的理想范围；同时离合器滑摩阶段的时间有所增加，离合器主动端转速不稳定波动，此时工况3的滑摩功损失增大至工况1的4倍.由结果分析可知，滑摩功损失的实验结果和模拟结果趋势相同，随着任务调度周期的增大，滑摩功损失大小均呈现几何倍数增长的趋势.

试验结果再次验证了，较小的任务调度周期能够获得良好的离合器接合品质，较大的任务调度周期则会导致滑摩阶段的冲击度和滑摩功损失增大.但是，总体上，当任务调度周期小于临界值时，离合器接合品质变化不大；而当任务调度周期超过临界值时，接合品质迅速恶化，车辆平顺性和部件耐久性都会被破坏.

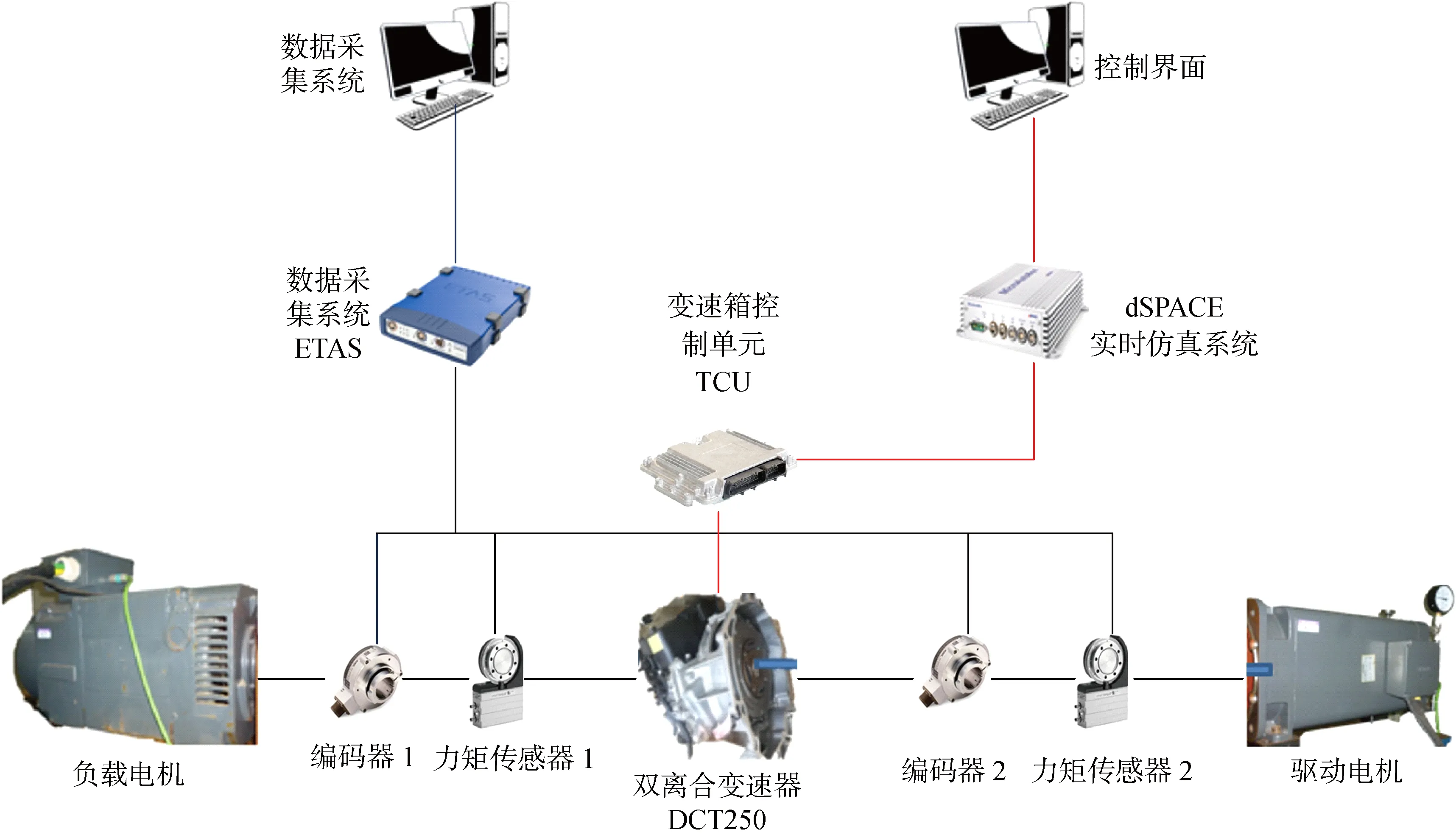
图6 台架试验设备Fig.6 Bench test facilities

图7 台架试验结果图Fig.7 Bench test results

5 结论

基于控制性能和实时调度协同设计的思想，在离散域内建立了闭环控制的离合器接合过程动力学模型，通过稳定性分析，得到临界任务调度周期.在MATLAB/Simulink模拟环境中以及传动台架上对不同任务调度周期下的系统动态响应进行了试验.结果表明，当任务调度周期小于临界值时，调度周期越小则接合过程的冲击度越小、滑摩功越小，但是总体上差别不大；而当任务调度周期超过临界值时，整车冲击度和滑摩功会急剧增大，将使得车辆平顺性和部件耐久性恶化.本文提出的方法，可为广泛采用电子控制器的汽车行业或其他行业提供参考.