高效RGB格雷码与相移法结合的三维重建技术*

皮金柱， 梁艳阳， 何宏森

(西南科技大学 信息工程学院，四川 绵阳 621000)

0 引 言

传统的三维模型测量手段主要有基于被动光测量和主动光测量。基于主动光的非接触式三维测量技术在现代工业中占据重要的地位且精度高于被动光的方法。主动光视觉按投射结构光的属性分为散斑、线结构光、光栅等，主动光视觉通过人为投射具有某种属性的结构光，来解决由于物体缺乏纹理而造成的测量困难。

文献[1]提出了一种基于面结构光的刀具三维测量系统，采用多频外差法与4步相移法结合的方法使系统获得了较高的测量精度，测量误差小于0.09 mm。文献[2]提出了一种双频相移三维测量方法，使用通过四步相移法求解包裹相位来建立条纹周期编号组合表，通过获得条纹周期数和利用条纹周期与包裹相位之间的数学关系得到绝对相位，实现解包裹。文献[3]中采用格雷码—相移组合的结构光，结合双目立体视觉技术的三维表面测量方法,重建结果验证该方法的准确性和可靠性。文献[4]针对牙齿的三维轮廓重建提出了一种基于张正友标定法提出一种快速、精确的相机与投影仪联合标定的方法提高系统的精度，测量误差小于0.1 mm。文献[5]中提出了一种双频相移与格雷码结合的方法，消除了测量过程中的由周期跳变导致的粗大误差，有效提高了系统的精度。

本文提出了基于RGB格雷码和相移法相结合的三维重建方法。采用RGB格雷码的编码方式进行条纹定级。与传统的二值格雷码与相移法相比，64级条纹之内仅需要3幅条纹图，有效减少了条纹图的幅数，减少解码周期提高重建的精度，更好地满足实时重建需求。

1 系统总体设计

系统的总体方案设计如图1所示， 首先当投影仪投射初始相位为0，π/2，π，3π/2的正弦光栅时，双目相机采集不同相位的图片。然后将3幅RGB格雷码条纹投射在立体模型表面，用同样的方式记录变形的格雷码条纹。

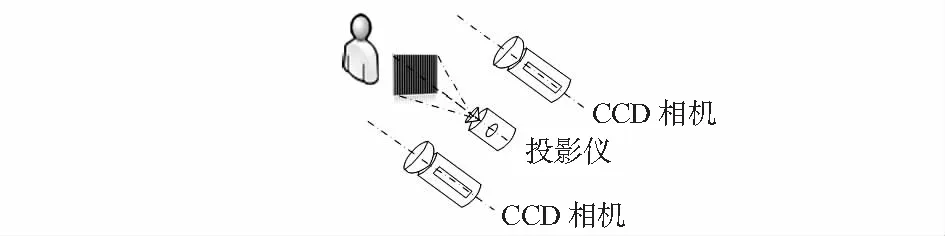
图1 系统平台设计

系统流程如图2所示，由于左右相机采集图片的顺序是已知的，分别计算相位主值和条纹级数，最后求出初始相位为0时，经立体模型调制后正弦光栅的真实相位分布，将左右视图进行立体匹配生成视差图。对双目相机进行标定，根据标定参数和视差图求出立体模型的三维点云。

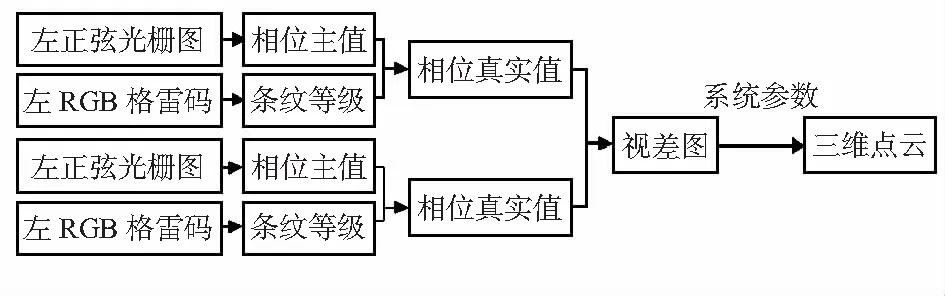
图2 系统流程

2 算法设计

2.1 正弦光栅解包裹

2.1.1 正弦光栅生成

本文使用投影机投射可编程的正弦光栅相移条纹[6,7]。当投影系统的光强分布满足余弦分布时，其光强则可表示[8]为

F0(x,y)=A(x,y){B(x,y)+C(x,y)cosφ(x,y)}

(1)

式中A(x,y)为物体表面的反射率，B(x,y)为背景光强，C(x,y)为条纹幅度，φ(x,y)为初始相位。本文采用四步相移法[5]，需要4幅相位间隔π/2度的条纹图。通过大量的实验数据分析确定采样间隔为一个像素点。由于该系统对立体模型的轮廓进行测量时，其深度信息相对变化幅度较大，故选取的采样周期应较大一些，本文选取的采样周期为1/32。设T为采样周期，在光栅原图中每一个点赋值Fi(x,y)

Fi(x,y)=127.5+127.5sin(i2π/T+0.5tπ)

(2)

式中t=0，1，2，3分别为4次相移。生成的正弦光栅如图3所示。

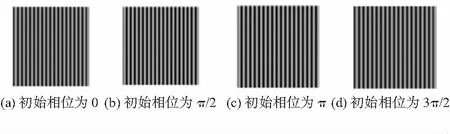
图3 正弦光栅

2.1.2 正弦光栅相位主值解包裹

正弦光栅的解码包括相位主值的求取和真实相位值的展开两步[9]。在本文中采用四步相移法计算包裹相位,在采集变形光栅图片时，由于受到现场环境和采集设备的影响，采集的图像中会存在失真及各种噪声点。使得到的光栅图像中会产生一些错误灰度值，这种情况对整个测量结果造成不利影响。经分析图像的主要噪声点为斑点噪声，因此要在解码之前先对采集的图像进行中值滤波[10]。由于正弦光栅投射到漫反射物体表面后，CMOS相机获取的变形光栅图像满足式(1)，根据式(2)可以得到相位差为π/2的4幅变形光栅图片，由式(2)可得

(3)

(4)

从式(3)、式(4)可以计算出n帧相移的相位函数[7]

(5)

本文选择四步相移法，故n=4,根据式(5)解得相位主值为

(6)

根据式(6)求得左相机图像进行相位矫正后的相位主值分布。

2.2 RGB格雷码的编码与正弦光栅定级

2.2.1 RGB格雷码编码

传统的利用格雷码编码的图像中只包含黑、白两种颜色的条纹[11]，编码所需要投影的编码图像数多，解码所需时间长。本文采用RGB格雷码对光栅条纹进行定级，为使条纹之间的差别达到最大,本系统投射的彩色条纹只采用每一通道的最大灰度255,即使用三基色红(255,0,0)、绿(0,255,0)、蓝(0,0,255)和(0,0,0)来编码。使用三基色编码使系统的噪声大大减少,有利于图像正确解码得到可靠的数据。本文的编码如图4所示，其中01代表RGB通道值为(255,0,0)，11代表RGB通道值为(0,0,255)，10代表RGB通道值为(0,255,0)，00代表RGB通道值为(0,0,0)。

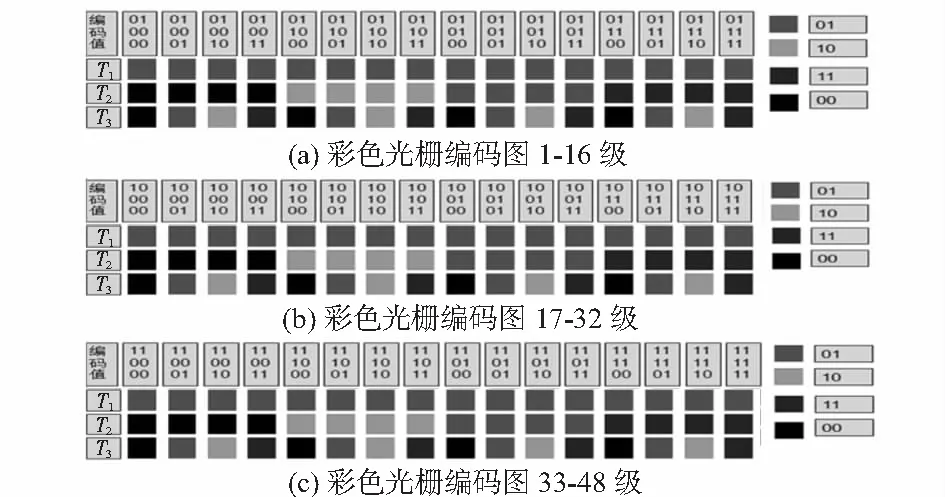
图4 彩色光栅编码

同理，第二级条纹在T1，T2，T3时刻条纹的RGB通道值分别为(255，0，,0)、(0,0,0)和(255，0,0)，以此类推。第一级条纹在T1时刻投射三个通道值为(255,0,0)的条纹，在T2时刻投射三通道值为(0,0,0)，T3时刻投射三通道值为(0,0,0)的条纹。根据图4的编码原理，可以生成相对应的三幅格雷码图片，如图5所示。

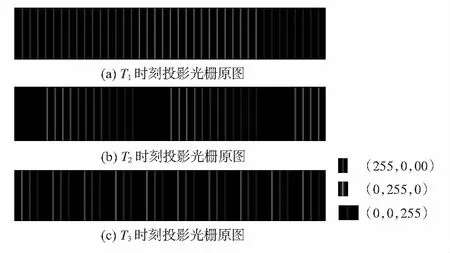
图5 光栅原图

传统方法在基于二值的格雷码编码时需要投射log 2n幅图片[9](n为条纹级数)，而本文的方法有效地减少了投射图片，仅需要log 4n/3+1幅图片，很大程度提高了测量效率。

2.2.2 正弦光栅条纹定级

四步相移法是利用反正切函数求解相位主值，因此，所求得的相位都被折叠在[π,- π]之间。存在跳变和不连续的状态，需要对折叠的相位进行展开，才能得到连续分布的真实相位值[10,12]。

本文采用RGB格雷码对正弦光栅相位进行展开。根据式(2)可知，sin(i2π/T+0.5tπ)=0时，解得i值Ii，其中Ii为每个周期的正弦光栅条纹中心处。 由于正弦光栅与RGB格雷码的节距和位置是一样的，故格雷码条纹中心与正弦条纹中心重合。 由图4知，正弦光栅第一级条纹中心编码为010000，第二级为010001，第三极为010010，以此类推，第64级为111111。采集t1时刻经物体高度调制的光栅图片，将RGB光栅图片的三通道转换为单通道，并用灰度重心法提取条纹中心线[13,14],根据条纹中心的位置，对比t1，t2，t3时刻对应位置光栅图的三个通道的像素值，根据式(8)得到条纹中心处每个像素对应的编码值。分析格雷码条纹中心处和非条纹中心处的像素的灰度值，得到解码时所需的阈值Th,Tl。对照图4的编码列表，由式(7)、式(8)可以解出条纹级数K为

K=P1+P2+P3

(7)

式中Th设为最大值，Tl为最小值，r,g,b为对应光栅图片的R,G,B通道值。

2.3 正弦光栅相位真实值求取

由式(2)得到正弦光栅的相位主值φ，由式(7)求出正弦光栅条纹级数K，将φ和K带入公式(8)可以得到相位真实值φ

φ=φ+2Kπ

(8)

2.4 基于真实相位的立体匹配

本文采用张正友平面标定法求出相机的内参数和外参数，然后求出左相机到右相机的旋转平移矩阵R,T。由于在双目的左右视图中，每一行中每个像素的φ值是唯一的，根据双目视觉原理的极线约束条件知，左相机相位分布图中的每一个点在右相机相位视图的极线上都有唯一的点与之相对应，逐点求出视差值得到的左视图的视差图。

3 实验与结果分析

实验平台采用Inter i7730处理器，三菱MD—565X投影仪，BASLER PIA 2400工业相机，分辨率为1 280×1 024，实验中的立体模型采用的是立体的人脸石膏模型。

采用张正友标定法对相机标定，双目相机拍摄14幅以上个不同位置的棋盘格标定板图像。求出左右相机的内外参数矩阵。

双目标定完成后，将正弦光栅投射于待测物体表面，得到4幅相位差为π/2的光栅编码图案，如图6(a)～图6(d)所示。根据式(6)求得正弦光栅的相位主值，并将相位主值归一化为(0～255)，得到相位主值分布图，如图6(e)所示。

图6 正弦光栅编码

相位主值具有周期性不能用于立体匹配，需要用RGB格雷码将相位展开。将3幅格雷码图案按顺序投射于被测物体表面，得到求取相位真实值所需要的编码图案，如图7所示。

图7 RGB格雷码与相位

由实验得知，投射RGB通道值为(255,0，0)，(0,255，0)，(0,0，255)的条纹，得到的真实通道为230以上，投射RGB通道值为(0,0，0)的条纹，得到的真实通道为30以下，故式(8)中的Th,Tl设置为230和30。完全满足根据RGB通道值大小为解码依据的要求。根据图7和式(7)，可以解得每个条纹的编码值，然后对照图4的解码方式，可以确定每条格雷码条纹的级数K。将K值和由式(6)求得的φ值带入式(8)，得到正弦光栅的真是值分布图，如图7 (d)所示。

本实验中条纹级数为64级，多频相移法解码所需的图片数量至少8幅[1]，二值格雷码与相移法需要投射的条纹幅数最小为11幅[3,4]，因此，传统格雷码与相移法比多频相移法的运算效率低，但精度比多频相移法高。本文方法可以直接进行相位主值求取和对条纹级数定级，且64级条纹之内需要投射的格雷码条纹图片为7幅。本文方法在条纹定级时仅需要3幅条纹图，提升了重建的速率。为了验证本文提出的算法的优越性，本文方法和多频相移法以及传统二值格雷码与相移法分别对投射有正弦光栅的模型进行相位解包裹和三维重建。分别从时间和点云精度及视差图效果做对比，由实验结果得出，在同样的图片分辨率下，本文方法比传统二值格雷码与相移法、多频相移法效率更高。多频相移法需要在求出相位主值之后才能求取相位真实值，不利于并行计算，速率受到限制。 由图8(a)知，在同样分辨率的图片下，本文的方法比多频相移法的速率要高1.5倍左右，比二值格雷码与相移法的速率高1.2倍左右。本文算法和多频相移法及二值格雷码与相移法应用到同一标准球体表面的三维重建中，将点云拟合为球面并求出重建球面半径，重建半径与标准半径做差得到重建误差，连续测量10次得到图8(b)所示的误差分布图。可知本文方法的精度可以达到0.025 mm，比多频相移法和二值格雷码与相移法的精度分别提高了0.02 mm和0.03 mm。

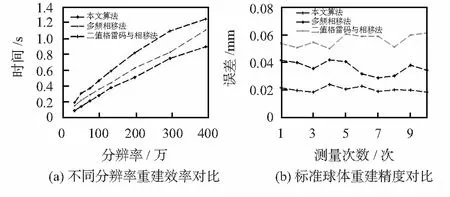
图8 各算法性能对比

将该方法应用到标准平面的三维重建中，如图可知本文方法噪声低于多频相移法及二值格雷码与相移法。利用三种不同方法重建模型的视差图，本文的方法点云稠密，噪点少。根据双目相机标定参数和视差图，得到模型的三维点云，如图9所示。

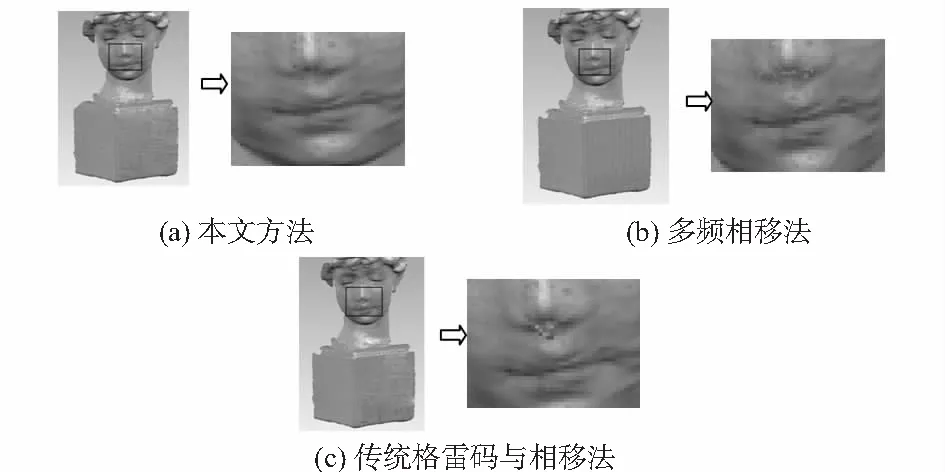
图9 三维模型点云及局部点云对比图

4 结束语

本文提出了一种新的RGB格雷码编码方式，该方法在64级条纹之内将解码需要的投影条纹数量减少到3幅，提升了传统格雷码和多频相移法的相位解包裹精度和效率。后续将对重建过程中存在的噪声和传感器融合的精度进行深入研究。