基于检验方程下的单步法稳定性分析
闫述涛
(中国传媒大学理工学部,北京 100024)
1 引言
在一阶微分方程的求解当中,稳定性是一个必须要考虑的问题,它对最终初值问题的解产生直接的影响。求解微分方程的初值问题所用的Euler法、后退的Euler法、梯形法、Runge-Kutta法,通常采用差分格式进行求解,这样就不可避免的在计算的过程中产生误差,随着计算过程的不断进行,误差可能就会逐渐累积,影响最后结果的精确性。因此我们要对数值解法进行稳定性分析。
2 稳定性的定义
当在第i个点上xi的yi值存在值为δ的误差时,如果在第i个点后的各个点xj(j>i)上的值yi存在的误差都小于等于δ,则称该方法是稳定的。
稳定性不仅跟算法相关,也跟步长的大小相关,同时也跟方程中的函数f(x,y)相关,为了简便分析过程,构建一个模型方程,利用解模型方程的稳定性来确定方法的稳定性。
设模型方程为
y′=λy
(1)
其中λ为复数。同时为保证微分方程本身的稳定性,我们假设Re(λ)<0。对方程y进行局部线性化变换,例如在区间(a,b)上,方程可以改写为
(2)
省略高阶项,再次进行变换,就可得到(1)式。
3 Euler法的稳定性分析
Euler法的公式为yn+1=yn+hf(xn,yn),h是步长,我们现在通过模型方程来考虑Euler法的稳定性。我们有

(3)
合并之后有
yn+1=yn+hλyn
(4)
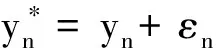
εn+1=(1+hλ)εn
(5)
要保证方程是稳定的,就要求误差是不增长的,即
(6)
整理得-2 后退Euler法,其计算公式为yn+1=yn+hf(xn+1,yn+1)(7),将模型方程带入公式,我们有 (8) Runge-Kutta法有很多不同形式的计算公式,我们在这取最常用的四级四阶Runge-Kutta公式,它的计算公式为 (11) 将模型方程带入(11)中,我们有 可得,Runge-Kutta公式的稳定区域为(-2.785,0) 计算方法表达式稳定区间Euler法1+hλ(-2,0)后退Euler法11-hλ(-∞,0)梯形法1+hλ21-hλ2(-∞,0)四级四阶Runge-Kutta法1+hλ+(hλ)22+(hλ)36+(hλ)424(-2.785,0) 由对比我们可以清楚的看到,四种常见的微分方程求解方法当中,后退Euler法和梯形法的稳定性较好,并且隐式方法比显示方法在稳定性方面要好。 Euler法、后退Euler法、梯形法以及四级四阶Runge-Kutta法都是微分方程的最常见的求解方法,四种方法的收敛性、稳定区间不同,因此在求解方程时,可以依据不同的方程结构选择合适的求解方法。4 后退Euler法的稳定性分析
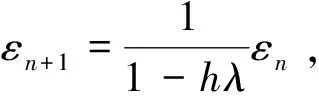
5 梯形法的稳定性分析
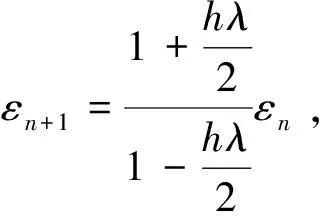
6 Runge-Kutta法的稳定性分析
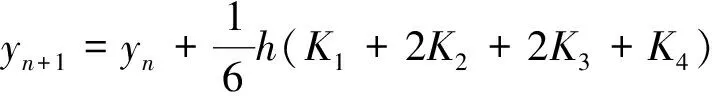
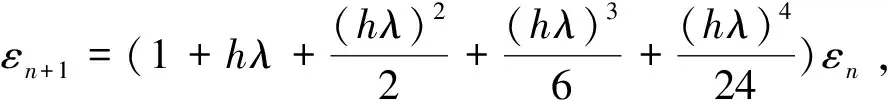
7 四种方法的稳定性对照
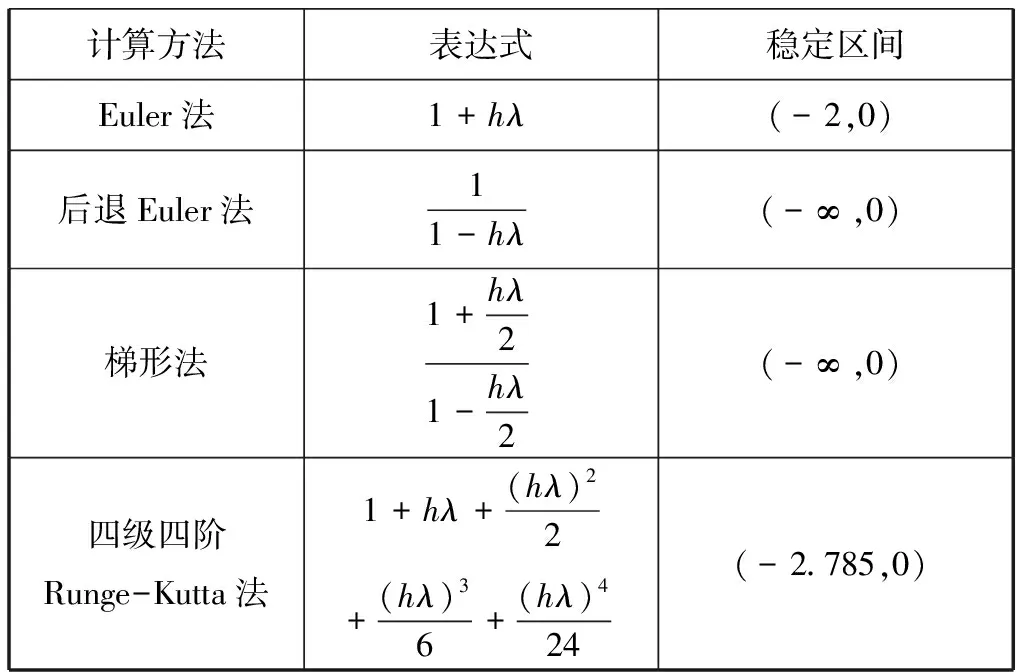
8 总结

