单光子技术理论与应用的若干问题

黄志洵

(中国传媒大学信息工程学院，北京100024)

1 引言

1905年A.Einstein[1]提出光由光子组成的假说，百年后它已是量子信息学(quantum information technology，QIT)研究中不可缺少的粒子。迄今对光子的研究是成绩与问题并存。值得注意的是，Einstein在1951年(72岁时)给老朋友Besso的信上说[2]：“整整50年自觉思考没有使我更接近于解答‘光量子是什么’这个问题”。的确，光子的理论和本质性的认识至今尚未解决好[3]，而单光子在QIT中的应用却已铺开。在这种情况下，我们对单光子的理论及应用再作讨论是必要的。

多年来，笔者对光子的有关问题怀有强烈的兴趣，写过一些文章作为讨论[4-8]。2018年，笔者又发表了两篇QIT方面的文章：“试论量子通信的物理基础”[9]，“试评量子通信技术的发展及安全性问题”[10]；本文在以上两文的基础上写成，论述单光子理论与应用的进展和存在的若干问题。

2 光子是经典性微观粒子还是量子性微观粒子

光子不是宏观物质粒子而是微观粒子。所谓经典性微观粒子是指：用经典物理原理即可推导出基本方程并作解释、用经典物理方法即可进行基本实验的微观粒子，以与不能这样做的纯量子性粒子相区别。那么光子是哪一种？至今仍然不甚清晰。

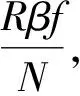
Einstein的光子与Planck的量子有所不同。1900年M.Planck的工作只是使构成黑体壁的振子的振动能量子化，或者说他的能量子只是一种为导出辐射公式所用的计算工具。Einstein则把光量子当成一种物理实在，是电磁辐射和光的基础。Einstein的出发点是黑体辐射理论面临的困难，以及Planck对基本量子的确定。从Wien的黑体辐射定律出发，有

ρ=αf3e-βf/T

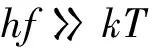
(1)

假定能量为E的辐射的频率介于f到(f+df)之间，占有体积V，则可导出能量不变时辐射的熵随体积变化的关系：

式中S、S0为辐射占有体积为V、V0时的熵；故单色辐射的熵随体积而变化。上式又可写成

(2)

式中R为气体常数；N为1mol的分子数。引用Boltzman原理(该原理说一个体系的熵是其状态的几率函数)：

(3)

最终导出某瞬时全部辐射能集中在体积V0的部分(V)中的几率为

(4)

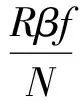
用这些观点，Einstein成功解释了光电效应、光致发光、紫外线致气体电离效应。Einstein光量子的能量为

(5)

对比Planck于1900年导演辐射公式时提出的能量子：

E=hf

(6)

如果两个理论吻合一致，就有

(7)

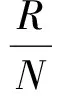
光子的特性由对应光波的频率f所决定，看起来是一件奇怪的事情。然而这个理论出色之处正在于此，它使用Maxwell理论解释不了的光电效应得到了完全的阐释——当光照射金属表面时，逸出的光电子的动能、速度仅与光频有关，而与光强无关。

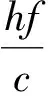
经由两个Nobel奖的表彰，Einstein有理由为提出光子学说感到自豪。然而发生在1925年的一件事改变了他的想法；2004年科学史家M.Chown[11]的文章说，今天没有多少人知道Einstein对巴西的访问；那次旅行是1925年3月5日从汉堡(Hamburg)出发的，做3个月的南美之行。当时，巴西科学家们齐聚在里约热内卢(Rio Janeiro)，期待着听Einstein讲相对论。但他本人却另有想法；对Einstein而言，相对论只是19世纪经典物理学的扩展，而在他一生中的革命性成果却是光子概念，这才是他要讲的东西。报告结束后，听众中有人提问说：“波伸展在整个空间，而粒子却是分立的实体，如何统一这两者？”Einstein不知道，因而回答不了。由于Einstein使用经典物理学，这是不可能做到的。在Einstein巴西演讲的一个月后，德国的W. Heisenberg发明了一种新的物理学，即量子力学。Einstein看不到(不能看到又不想看到)的要点是，光子不是一个经典的东西。1925年5月7日在巴西科学院作报告的那个夜晚，标志着Einstein作为前沿科学家生涯的终结。直到去世，Einstein都不接受量子力学，该理论用不确定性取代确定性。Einstein在里约热内卢的演讲表示他仍绝望地希冀他于1905年放出的“妖怪”(光子)，还可用老的经典物理去驯服。

Chown说的这件事是Einstein在巴西科学院演讲结束后回答提问时遭遇尴尬，因为情况确实如此——无论当时或以后Einstein都写不出一个能统一说明光的波粒二象性的方程。以后的事态发展是量子力学(QM)于1926年至1927年间横空出世；按照新的理论，交变电磁场、电磁波可以被量子化，从而在波与粒子之间建立一条通道。在量子理论中，光子是量子化电磁场的元激发粒子(photon is the elementary excitation particle of the quantum electromagnetic field)；因此首先要对电磁场作量子化处理[12]。

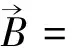
(8)

(9)

在Coulomb规范下有：

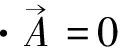
写出Lagrange密度：

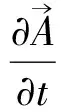
(10)

注意积分号内的H为磁场强度；现在用正交模函数展开，得

(11)

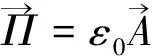
(12)

(13)

经过量子化处理，Hamilton算符为

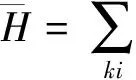
(14)

经过量子化后的光子场可以用光子数表示；光子无确定位置，但有确定动量和偏振方向。表示光子数态的写法是|nk〉，对应Hamilton算符的本征态，故有

|=ћ

(15)

光子数算符(k模式)为

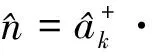
(16)

以上各式中|nk〉代表nk个光子的状态，而其光场平均值为零(例如电场测量平均值为零)，但光强的平均值不为零。

以上分析只考虑了电磁场振幅而未考虑相位，可以引入光子相位算符并作分析。这里从略。总之，态|nk〉是光子数，是确定的；但光子数与相位是一对测不准量，故相位是不确定的。

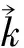
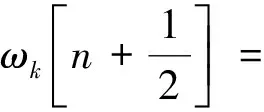
(17)

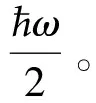
实际上是说零点能量为

这与其他方法推导零点能的结果一致。

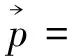
现在，光幅射场是占据一定空间的大量光子的集合，而其中的光子分别处于一定数目的、可区分的量子状态之内。每个状态内的平均光子数称为光子简并度，它表示到底有多少性质全同的光子共处于一个量子状态内。自然光的简并度很小，例如太阳光为10-2级；而激光的光子简并度可高达1020。

用量子理论描写光并不降低Maxwell方程组(ME)的价值，因为量子系统的量子数足够大时其行为就接近经典力学(CM)和ME的描述。理论上也可考虑经典与量子互相结合，例如把ME与Schrödinger方程(SE)联合求解，以处理电磁源和物质系统同时存在的情形；当然这在数学上困难很大。

那么，单光子是经典性微观粒子还是量子性微观粒子？这个问题难以回答。尽管Compton实验证明了光子和电子一样都是物质实体，具有正实数的动质量，又证明了在微观粒子的单个碰撞事件中动量守恒、能量守恒；但光子却不是一个弹子球，不能主要依靠经典物理学去处理。例如，如果企盼“测出光子直径”，恐怕难有结果。按照熟悉的宏观概念去看待光子是徒劳的。从本质上讲光子属于量子世界，在这个世界里粒子和波的区别变得模糊，“大小”的概念似乎不再有意义。人们用数学来描述光子的表现，但却无法把光子形象化为常规的图像。

3 光子是不是点粒子

在现有理论中，光子是确实存在的、可感知的粒子。例如1955年R.Stacy[13]在其生物物理学著作中说，通常进入人眼(瞳孔)并能造成视觉的光子数为54个～148个。假定是100个光子，那么能量相当于3.2×10-10erg，这是整个眼的敏感度。考虑到一些复杂的反射、吸收过程，可算出，在绝对闽值时光感物吸收的光子数仅为5个～14个，说明人眼的构造高超，敏感度惊人。实际上，只需单光子即能激活一个圆柱细胞，但在5个～14个圆柱细胞同时被激活才能引起光感。但这些估计是在能量水平上进行的；这里有必要讨论光子能量以及其另一重要参数——光子动质量。

前面给出了认识光子的基本方程；联立E=hf和E=mc2两式，可得

(19)

故Einstein理论认为光子动质量仅取决于频率f；而在传播方向上，光子的动量为

(20)

这种质量、动量推导使光子形象粒子化了。由于c很大，故除非f很大，否则m和p都很小。至于光子能量，可用下式计算：

(21)

式中f、λ分别为光子对应波动的频率和波长。因此可以算出光子的动质量和能量，见表1。可见，在从微波到X射线的广大波段，光子质量都比电子质量小(电子静质量m0=9.109534×10-28g)。表1中光子能量用电子伏(eV)作为单位，而1eV=1.60217733×10-19J，故在可见光谱的中点(λ=5×10-5cm)，可算出E=2.48eV，可见单光子的能量很小。需要说明的是，处在微波(microwaves)与可见光(visible light)之间的区域现在通常称为太赫波(tera waves)，频率f=100GHz～30THz(1THz=1012Hz)，而1THz对应的光子能量为4.1×10-3eV。

表1 光子的动质量与能量

但现有理论非常不令人满意，因为它把光子描写成既无形状、体积，又无静止质量的奇怪粒子。同样是微观粒子，为什么人们可以指出电子的尺寸和确定的静质量，对光子却说不出来？任何物质实体都会占据一定空间(即使很小)，光子却似乎可以在无自身大小情况下而分布在空间区域之内；这样的理论怎能令人满意？！

在狭义相对论(SR)中有运动体长度缩短公式[14]：

(22)

式中v是运动速度，l0是静止时物体沿运动方向的长度，c是光速。对光子而言v=c，故l=0；因此Einstein光子无体积(尺缩到零，成为一个点)。光子作为一种有动质量、动量、能量的粒子，却无体积，这一观点意味着光子成为点粒子；这无论如何不会是好理论。物理学的发展史曾提供过把电子当作点粒子时的教训。众所周知，量子场论(QFT)和量子电动力学(QED)被人们认为是很有成就的学科；然而QFT和QED的短板是著名的发散问题，根源在于这是一种点粒子场论。梁昌洪[15]在对经典场(静电场)的自作用能问题作论述时指出，早在1940年R.Feynman就注意到“电子自作用能无限大”给电磁场理论造成了突出的问题，而这是由于描述电子的模型是点粒子。这就是说，点电荷的自作用存在发散困难。如把电子看成没有结构的点，它产生的场对本身作用引起的电磁质量就是无限大。……1964年P.Dirac[16]关于QED的演讲中谈到重整化，他首先论述的正是这个电子质量问题。电子质量当然不会是无限大，不过电子与场相互作用的这个质量会有变化；Dirac指出，无法对“无限大质量”赋于什么意义。人们在“去掉无限大项”的情况下继续计算，得到的结果(如Lamb shift和反常磁矩)都与观测相符；因此就说“QED是个好理论”，不必为它操心了。Dirac对此极为不满，因为所谓“好理论”是在忽略一些无限大时获得的——这既武断也不合理。Dirac说，合理的数学允许忽略小量，却不允许略去无限大(只是因为你不想要它)。……总之，Dirac认为QFT的成功“极为有限”。

实际上电子不是点粒子，著名实验物理学家丁肇中曾长期关注电子的尺寸测量问题，不久前他给出的数据仍为电子半径r≤10-17cm。那么电子是否呈圆球状？丁先生未说。……光子与电子不同，后者有确定的静质量而前者没有(主流的物理界观点认为没有)；另外，电子带电荷而光子不带电荷。尽管如此，规定光子是点粒子也会发生问题，只是暂时未对此作深入分析。……关于量子场论存在的问题可参考王令隽[17]的论述。

4 光子和电子的比较

把光子和电子作全面比较，是很有意思的。它们都是微观粒子，都有极广泛的应用；电子学(Electronics)、光子学(Photonics)都是著名的庞大学科。然而，这两种粒子的特性却很不相同。为了讨论的方便，我们给出两个表——表2是光子和电子研究情况及理论思想的比较，表3是电子学与光子学这两大学科的比较。

表2 光子和电子研究情况及理论思想的比较

光子和电子突出的区别是，电子有确定的静质量(而且有精确的测量值)，而光子的静质量被认为是零。在狭义相对论(SR)中，任何以光速c运动的物体，其静质量必须为零[18]。因此光子的m0=0是逻辑推理的结果，而不是由实验所决定的。实际上，科学界对光子静质量的测量从未停止[18-22]。有的科学家(例如美国物理学家R.Lakes)甚至以此作为毕生的研究方向。

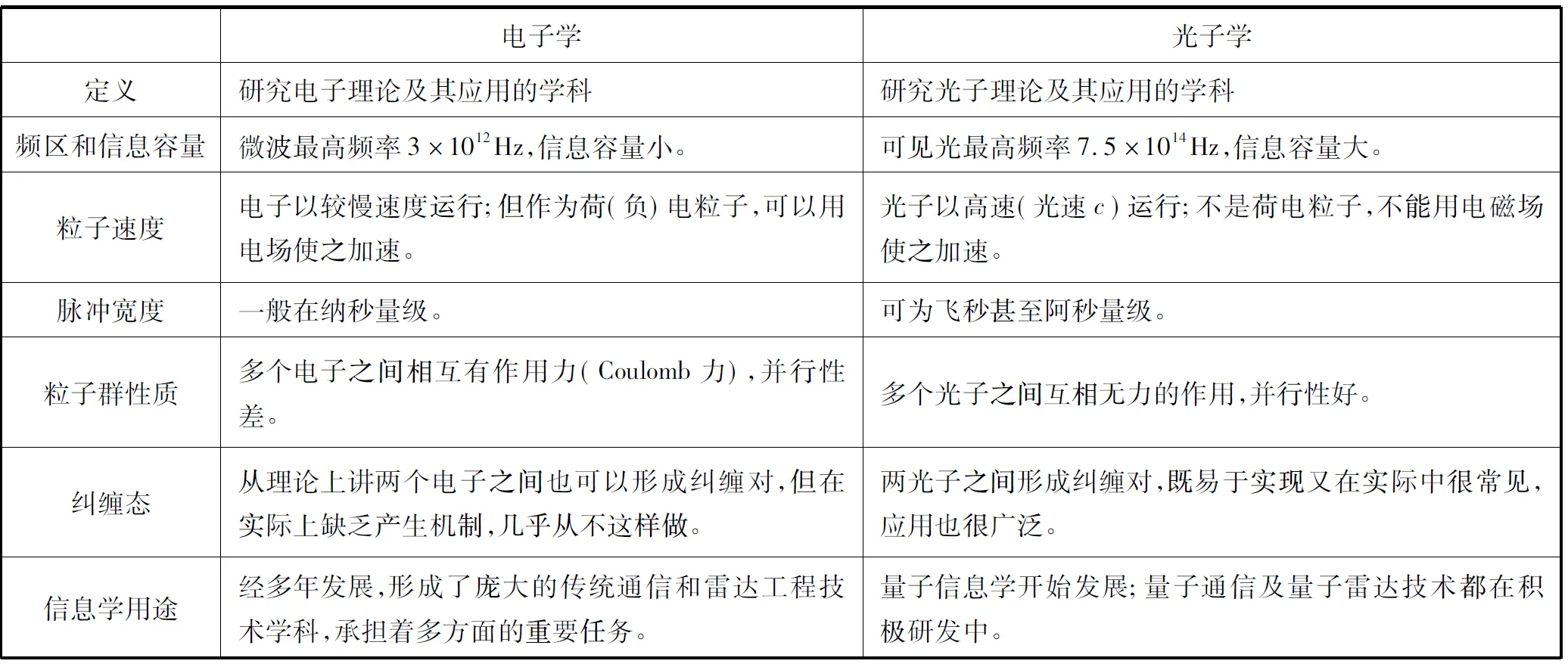
表3 电子学与光子学两大学科的比较

表2及表3说明，光子与电子的不同远多于它们的相似。现在，有必要就波方程及波函数方面深入讨论。先写出经典的Maxwell波方程[23]：

(23)

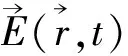
(24)

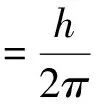
(25)

这是在1928年导出的波方程，我们称之为DE。

量子力学家张永德[26]认为，DE作为单电子波函数方程，只计及外部电磁场作用，未考虑电子自身的电磁作用，故仍是近似方程。其次，它不能推广应用于光子，因为Dirac假设粒子位置是可观察量。对光子此假设不成立，无法对光子问题定位描述。光子没有真正意义上的坐标表象；虽然有时对光子强行引入包含力学变量的准波函数描述，其实它没有一个通常的波函数物理解释(模平方是几率密度)。但光子可以有动量表象的描述，这对实际目的已足够。……实际上他是说无法为光子定义一个自洽的波函数，也没有光子的几率波性波方程(电子则有)。

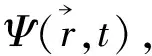
Lanzagorta还说：“the photon is a non-localizable particle”；又说：“the photon cannot be localized”；这些话的意思与张永德所述一致。进一步，Lanzagorta指出光子与一般微观粒子(如电子)的区别。这是因为在数学上无法用满足Einstein狭义相对论(SR)的局域性几率分布来建立连续性方程(it is a mathematically impossible to build a continuity equation using localization probability distributions that satisfy Einstein’s special relativity)；既然无法建立连续性方程，所以无法为光子写出波方程(it is impossible to write down a wave equation for the photon)。可见，研究光子比研究电子更困难。

5 光子静质量与Proca波方程

光子(photon)和中微子(neutrino)是两种至今仍然令人产生神秘感的粒子。它们是否有非零(但微小)的静止质量，一直是引起争论的课题[18-22]。传统的物理理论如Maxwell电磁理论和狭义相对论(SR)，认为光子没有静止质量，即m0=0；因此，光子被称为“无质(量)粒子”，以区别于像电子这样的“有质(量)粒子”——后者也被称为物质粒子。

尽管测量光子静质量的努力从未停止，而且像量子电动力学(OED)这样的理论也作了光子静质量不为零的假定[22]；人们仍然认定光子是无质粒子。现在看来，这或许不仅是认识光子的障碍，而且还是造成基本物理理论自洽性缺失的原因之一。

粒子物理学通常假定Lorentz-Einstein质速公式为真[15]：

(26)

式中v是粒子速度，c是光速，m0是v=0时的静止质量(rest mass)。物理学教科书从未说过上式不适用于光子，因此人们不妨一试；取m0=0、v=c，则有m=0/0；m成为任意大小，是不可接受的。问题只能出在以下三方面：①质速公式不对；②光子静质量不是零；③光子运动速度不是光速c。显然这三者任何一个成立都与狭义相对论(SR)不符；实际上，Einstein用自己的理论(SR)却解释不了自己发现的粒子(光子)。

基础物理理论的尴尬还有下述内容：作为量子力学(QM)的重要组成部分的Schrödinger量子波方程(记为SWE或SE)和Dirac量子波方程(记为DWE或DE)，其中都有粒子质量m，而Maxwell波方程(记为MWE)中却没有质量。当然，在Maxwell的时代(1865年)没有波粒二象性(wave-particle duality)概念；但我们现在有，那么怎么办？SE、DE是非常成功地描写了电子运动的波方程；对照以下情况——电子是有静质量的微观粒子；SE、DE在方程表达式中都有质量参数m；这两点具有内在逻辑的一致性，也是对波粒二象性这一根本性物理现象的极好诠释。……但MWE中没有质量参数m，这是否说明Maxwell方程组不够精确、需要修正？……此外，自1970年光纤(optical fiber)问世后，用SE作阐述取得成功[28]；这说明SE可用于分析光子参与物理过程的现象，但这里有一个问题：SE中的m是什么呢？……最后，微观粒子的波动性取决于其统计性，波函数所代表的只是几率波。这原理对电子而言正确；对光子则出现悖论——虽然光子是电磁场、波量子化的结果，而电磁波却不是几率波。这样一来，“波函数模平方是几率密度”不适用于光子；那么光子还是微观粒子么？如果是，怎样体现其统计性质？

必须指出，如果取光子为有静质量(但非常小)的粒子，上述悖论均迎刃而解，理论体系的自洽性就大为改善。现在有许多物理学家不相信光子m0=0，例如美国Wisconsin大学教授R.Lakes一直从事测量光子静质量的研究，他曾坚定地说：“the photon is massive!” 现今早已不是Maxwell的时代了，ME和MWE会有变化，这一点并不令人吃惊。

1936年A.Proca[29]提出新的电磁场方程组是合乎逻辑的结果；当然，Proca假定对光子而言静质量m0≠0。本节即论述这个问题；并且，我们将推导光子专属的波方程。

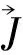
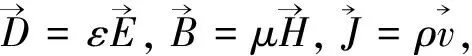
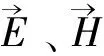
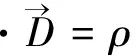
(27)

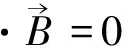
(28)

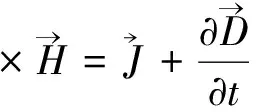
(29)

(30)

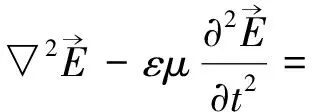
(31)

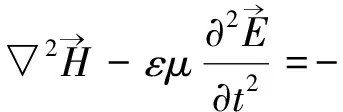
(32)

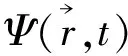
用类似方法可从Proca方程组的两个旋度方程出发而作推导；先写出Proca场方程组：

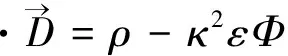
(33)

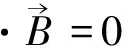
(34)

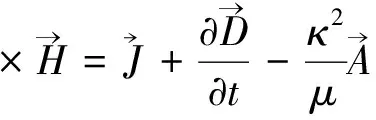
(35)

(36)

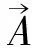
(37)

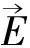
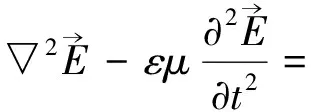
(38)

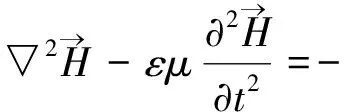
(39)

如果m0=0(κ=0)，那么Proca波方程回到Maxwell波方程。对于无源自由空间(ρ=0)，就有

(40)

(41)

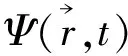
总之，笔者认为Proca理论对研究单光子有用，扩大了思路。虽然光子和电子很不一样；但如光子也是有静质量(即使非常小)粒子，就会像电子那样带有几率波特性。这一点我们从1933年Nobel物理奖授予者致词时所讲的话得到验证，他说：“引进光量子以后，量子力学必须放弃因果关系的要求。……物理定律所表示的是某个事件出现的几率——我们的感官和仪器不完善，我们只能感觉到平均值，因此我们的物理定律所涉及的是几率。”……既如此，笔者认为追求“光子几率波方程”并不为错——但这样的方程过去并没有。如承认光子波动具有统计性，那么它与经典波动(如力学波、声波)确实不一样，似乎亦不等同于电磁波。

由于Proca本人未作波方程推导，我们弥补了这一缺陷，给出了PWE；但提供的两个方程未有有统一的形式，如何在实践中应用也仍待研究。至于采用Proca理论后的其他影响，见文献[8][30]。这里仅着重指出，Proca波的相速(vp)和群速(vg)均与角频率(ω)有关，呈现出真空中电磁波的色散效应：

(42)

(43)

式中c为真空中光速，而ωc为特征角频率：

(44)

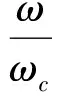
为了对微观粒子建立静质量的数量概念，这里提供一些数据——电子静质量me=9.10938188×10-28g，这是1998年国际推荐值(见：沈乃澂，基本物理常数1998年国际推荐值，中国计量出版社，2004)；然而，光子静质量上限的一个值2×10-50g[19]，另一个值是1.2×10-51g[20-22]。可见，光子静质量即使不为零，也比电子小很多：对照表1中的光子动质量数据，光子静质量也非常小。但m0≠0对基础理论的影响却很大。

6 光子数方程与光子数测量

经典光学(classical optics，CO)也承认光子并在论述中提及这种粒子，但从不考虑光子的数量问题。这是因为一束光(自然光或激光)中包含的光子数极大，谈论一万个光子如同提及大海中的一滴水，实在没有意义。量子光学(quantum optics，QO)则不同，它的思考细化到一两个光子的行为。近年来量子信息学(QIT)的发展更彰显了考虑单光子、双光子问题的意义。例如量子雷达(QR)理论中出现了“单光子QR”和使用纠缠态的“双光子QR”的概念；尽管它们在实际上尚未真正实现，但其想象力的新颖和大胆非常令人吃惊。又例如量子通信(QC)技术中使用了单光子串(单光子系列series of single photons)，也应用纠缠态，据说均已成功[9]；这也让人们有难以置信之感。

在QM中有所谓多体理论，例如考虑多电子时写出严格的量子场方程，然后再设法求解。多光子问题也是多体理论问题。总之，多粒子量子理论比单粒子量子理论更复杂、严格，因而也更高级。但这并不表示在单粒子时人们就很容易掌握。实际上，庞大粒子数的功能装备(如发射电磁波的经典雷达)更便于实现；而只用1个(或2个)粒子就能工作的装备(如单光子量子雷达)的成功不仅极其困难，或者竟是不可能。

那么1个波束(微波波束或激光束)中究竟有多少个光子？迄今为止尚无人测量过。这或许可以计算或估计；例如有说法是1018个光子，但我们不清楚其根据是什么。现在本文推导与光子数(n)有关的方程；前已给出单光子的动量为

不失一般性，对电磁波量子可写作

p=hk

矢量写法为

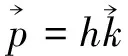
(45)

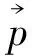
一束光的光子数如为n，则光子动量方程应写作

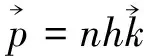
(46)

由此可得光子数方程：

(46a)

在频率(ω=2πf)为已知时，k的大小是确定的；然而，上式中p已不是单光子的动量，而是光束的动量。最近国外有报道说，加拿大科学家提出了测量光动量的新技术(见英国《每日邮报》2018年8月21日报道)，所指为光束的宏观动量，对我们的论题极有帮助。看看对这项新成果的介绍——“新技术首次测量光动量”。报道说，长期以来，科学家们一直怀疑光可能具有动量——结合质量和速度来衡量的一种特性。但光子据称是没有质量的。它们的动量如何对物质施加作用力，这在很大程度上仍是一个谜。德国天文学家J.Kepler于1619年首次提出，来自太阳光的压力可能决定了彗星尾巴的位置。彗星的尾巴总是指向远离太阳的方向。200多年后，J.Maxwell预测，辐射压力是由光的电磁场中的动量产生的。但从那时起，科学家们一直难以解释这种现象是如何出现的。

现在，加拿大不列颠哥伦比亚大学的科学家说：“我们之前一直没有确定这种动量是如何转化为力或运动的。由于光携带的动量非常小，所以我们所拥有的设备的敏感度一直不足以解决这个问题。”然而，一项新技术终于可以帮助解决这个有150年历史的难题了，它使用声学传感器来“聆听”穿过一面镜子的激光脉冲的弹性波。具体讲，研究团队制作了一面配备声学传感器和隔热层的镜子，以减少干扰和背景噪音。然后，他们向镜子表面发射激光脉冲，并使用声学传感器来探测运动的弹性波。研究人员指出，观察这种效果很像是观察池塘里的涟漪。他们说：“我们不能直接测量光子的动量，因此，我们的方法是通过‘聆听’穿过镜子的弹性波来探测它对镜子的影响。我们能够由这些波的特征追踪到光脉冲本身的动量，这为最终界定和模拟光动量如何存在于材料内部打开了大门。”

笔者认为，这项新成果实际上是设计了一种新装置来测量光子之间微弱的相互作用。这就为我们正在考虑的“如何测量一束光中的光子数目”这一课题提供了一条新的途径。而且，说每个光子都无质量但大量光子组成的光束却有动量，逻辑上说不通。尽管光束的宏观动量应是光子的动质量所造成，这项科学成果仍会敦促我们思考光子静质量的有无问题。

7 如何用实验技术掌控单光子

单光子是非常奇怪的粒子。迄今我们只能用一些抽象的物理参数(频率、功率、动质量、极化等)来描写光子，却无法使之具象化。光子什么样(是圆的、方的)？我们说不出来。光子有没有体积(即几何尺寸)？我们不知道。在通常情况下光子存在时间很短，这种飘忽不定的性质使它更难掌握。目前是依靠对脉冲的观察来间接了解光子，而这方法不是没有问题的。人们经常重复以下话语以掩饰自己的无知——光子不是刚性球，不是经典的东西；原始定义是一个能量子，只有量子理论才能对它作虽不理想但较好的说明，强调指出光子的非局域性(non- localized)。近20年来，单光子技术(single photon technology)有了很大发展，包括单光子的产生、检测和应用，都彰显了科学家们的智慧和努力。尽管如此，目前仍然没有理想的单光子源，QIT技术中常用的是近似单光子源。……可以说，目前的状况是理论认识的贫乏与应用技术的扩展并存。

单光子是一种最弱光源，具有最小的发光量。但我们又不能简单地说光子能量“小”，例如X射线光子的能量比微波光子的能量大108倍。为了有一种概括的了解，可以按可见光频率来了解光子能量的大致水平。单个光子的能量是1.6eV～3eV，这是按可见光的频率算出的。按2eV考虑，就有

2eV≈3.2×10-19J=3.2×10-12erg

这样就出现了一个问题：我们如把光束的功率逐渐减小，达到10-16W的水平，是否就能说“已获得了单光子”？……实际上，有的研究人员就是按此思路做实验的——2008年中国科学院西安光机所的张兴华、赵宝升等[31]实现了紫外单光子成像，现在根据他们的实践介绍单光子实验技术。单色光的光功率可用下式表示：

P=KE

(47)

式中E是一个光子的能量；系数K是单位时间内通过单位截面的光子数。显然，测量出K值是关键。当P不断减小，弱到以单光子发射时，只有用单光子计数模式，才能掌握单光子信息。当入射光功率减小到10-16W，光电探测器上的光电子脉冲呈不连续随机分布，此时光源为单光子发射。……虽然有人不相信这样即可得到单光子，但称之为近似单光子源还是可以的。

2007年3月14日法新社从巴黎发出电讯称，法国科学家发明了捕捉光子的装置，并且上百次成功地追踪到光子从产生到消失的过程，最长的达0.5s。在过去，虽然发现光子不难，但难以捕捉到光子——捕获时也就破坏了它。新的技术由法国科学研究所的Bruxell研究组完成，一个仅为2.7cm长的装置可捕捉一个光子并监控它从产生到消失的全过程。他们让一束铷原子穿过捕获光子的盒子，光子的电场会轻微改变原子的能最水平，但这不足以使原子从电场中吸收能量。当一个原子穿过光子的电场时，会使绕原子核运行的电子略微迟缓，而这一推迟时间可以使用现代原子钟技术测量，即把电子的轨道视为“钟摆”以测量出准确时间。

我们不怀疑这个实验的真实性，但仅看这个简略报道会让人产生许多问题。首先，实验者“捕捉到1个光子”是用什么来判定的？其次，单光子存在(也可称为“存活”)的时间最长只有半秒，说明它不是一种“产生了就呆得住”的东西——既如此，人们还怎能利用它来做工作(甚至承担某些重要的工程任务)呢？……实际上，判断单光子的获得是依靠光脉冲信号(甚至是由光脉冲转变而成的电子脉冲信号)。我们从未看到过这样的报道，即在某个实验中科学家获得了粒子形态的单光子。根本点在于，光子没有可视的具体形象。

2004年M.Keller等[32]发表文章，题为“在离子阱腔系统中用受控波形连续产生单光子”。实验的方法是：在光学腔体中使单离子被强烈局域化，以此为基础构建了单光子源，所用离子为40Ca+。实验系统使用了双镜片TEM00模腔、阱电极、声光调制器、雪崩光电二极管、分束器等。论文用脉冲波形代表单光子形象——这其实是唯一可行的办法，因为任何人也无法把1粒光子活灵活现地摆在人们面前。

重要的是光脉冲与光子数的关系，一个脉冲不一定代表一个光子。例如前述方法(把激光束经过强衰减后得到弱相干光)的这类光源中含有大量空脉冲和比例可观的多光子脉冲。然而量子通信(QC)技术中常用衰减的相干光脉冲作为近似的单光子源。由于相干光脉冲中光子数满足Poison分布，光脉冲存在一定的多光子几率，这使得对量子线路实施窃听成为可能，影响量子密钥分配过程的安全性。若要减小光脉冲中多光子几率，就必须将每个脉冲平均光子数水平降得很低(1%～10%)，使脉冲序列中有大量空脉冲(脉冲中光子数为零)出现。因此，这种近似的单光子源效率很低，严重制约量子密钥的生成速度和系统噪声特性[33]。

检测光子难度很大。1998年美国Stanford大学的科学家B.Cabrera用很薄的钨膜作为传感器，并使之冷却到超低温(8×10-2K)，从而成为超导体。当钨膜收到单光子，温度会略为升高，电阻略为增大，从而可以测量出来单光子的能量及到达时间。2003年美国标准与技术研究院(NIST)在技术上略有改变，用钨丝作传感器，成功地探测到单光子。

另一个例子是利用超导纳米线探测单光子。有一种技术是硅雪崩光电二极管单光子探测器(SPAD)，但性能差，对光子能量承受力低。2001年莫斯科师范大学Goltsman小组发明了利用超导线(纳米级)探测单光子的技术[34]，称为SSPD；当1个光子打到纳米线上，由于热点效应可快速产生一个电脉冲。这一技术暗计数率低(R<10-2s-1)，灵敏度高(小于单光子水平)，以及有其他优点，故受到广泛重视。这一技术被航天界所采用；地球上层空间的碎片数量极多，大小尺寸不一，是航天界非常头疼的问题。自2007年起上述俄罗斯研究团队已开始用SSPD取得了激光测距的成果，虽然距离只在数百米量级。中国科学院云南天文台目前已有激光测距系统；最新的研究表明[35]，使用SSPD技术有望使该系统实现空间碎片激光测距，对米级大小的碎片探测距离可达800km以上。

8 单光子技术应用于量子信息学及存在问题

虽然进行量子通信(quantum communication，QC)的信息载体从理论上说可以用各种微观粒子(如光子、电子、原子)，实际上，使用最多的是光子。这是因为光子的退相干容易控制，而且有利用传统光纤通信技术时的方便。QC技术中的源主要是单光子源和纠缠双光子源，这两者又有密切的联系。1984年C.Bennett和G.Brassard提出了用光子偏振态传送信息的量子密钥分发方案(BB84协议)；1989年C.Bennett又领导完成最早的量子密钥分发(quantum key distribution，QKD)实验；1991年A.Ekert提出了基于量子纠缠的QKD方法(E91协议)；这些成为QC的第一批基础性工作。由于进入新世纪以来的进步，QC已成为十分重要的学科，单光子源研发变得更突出了。

单光子源发射器件是实现量子密码通信的核心器件之一。由于目前缺乏理想的单光子发射器件，量子密钥通信的实验演示都采用激光衰减光源模拟单光子发射。衰减激光在实验上的困难不仅在于要搭建复杂光路系统，而且单光子产生效率很低，不能消除多光子的存在，无法避免受到多光子攻击的可能性。由于存在光子数分离攻击，最大安全通信距离都受到极大限制。因而，远距离量子密钥分发的实验结果原则上都有安全漏洞。如何得到一种稳定、高效、可靠的单光子源，已经成为量子通信和量子密码实用化的一个瓶颈。

2001年，E.Moreau等[36]的论文报道以量子点(quantum dots)为基础的固态单光子源。同年，英国剑桥大学(Cambridge Univ.)发明了由电流驱动的单光子源。这是一种新型的发光二极管，以称为量子点的电子群为基础，但它要求超低温条件，因而不实用。

2002年10月，C.Santori等[37]报道说，他们已解决了从小块固体物质中弄出几乎完全相同的一个个单光子的难题。我们知道，最简单的光量子计算也要求每个光子和其他所有光子都相同。这里所谓“相同”是指光子们一起达到同样的量子态，几乎无法区分彼此——在一般情形下做到这一点并不容易。Santori等人在砷化镓和砷化铟交错排列形成的5mm高的小柱上嵌入只有几纳米大小的点状砷化铟。当用激光照射小柱时，从点状砷化铟中激发出一个电子并放出一个光子。由于砷化铟的上下两层起“镜子”的作用，而电子在镜面间来回反射，发射的光子和下个光子都极为相似。

半导体量子点结构是—种典型的三维受限结构，体现类“原子”二能级体系特征，是制备单光子发射器件的理想选择之一。近年来，欧、美、日、中等多个研究组开展了单光子发射器件研究并有所进展。

QC技术如何抗杂散光的干扰是一个突出问题，特别在用卫星实现QC操作时。对此，笔者表达了很大的疑虑[9]。

传统雷达(classical radar，CR)经过近80年的发展已成为庞大、成熟的工程学科，拥有许多研究所和工厂，广泛应用于军事和民事领域。近年来兴起的量子雷达(quantum radar，QR)企图用少量光子做原本用电磁波完成的工作。QR比CR实现起来困难得多[27，38-41]，那么为什么要舍易求难？据说QR有许多优点，甚至能探测军用隐身(隐形)飞机。不过我们还未看到QR被研制出来并投入实战的报道。

从表面上看，QR与QC相比，前者没有保密(防窃听)要求，对单光子源没有太严格的限制。但QR发射的是多个单光子脉冲形成的阵列，不是依靠1个光子(only one photon)就可以工作的。而且，没有证据表明研发QR技术比研发QC技术更容易，因为雷达有其自身的一些苛刻要求，例如探测距离、分辨率、对隐身(隐形)的目标的可视性等。近来国外雷达界有一些动向——2014年，意大利开发出完全基于光子的全数字相干雷达(PHODIR)；2018年媒体报道俄罗斯为第6代战机研发光子雷达，用微波的X波段，是无线电波成像。我们不能肯定它们是量子雷达(QR)，但可以看出这类研究的军事意义。

2012年，M.Lanzagorta指出[27]：“These systems rely on quantum states of light(photons)sustained on an entangled superposition. One half of these states is send towards the target and the other remains in the receiver.”(系统依赖于纠缠叠加的光(光子们)的量子态；一半光子被发送至目标，而另一半仍然留在接收机内。)在这段文字中，光子是多数词而非单数词，故QR是制备出许多对双光子，孤立地看每对都处于纠缠态；而在雷达工作时，射向目标的为一个又一个单光子脉冲形成的系列，这样收到散射回波的可能性就大一些，尽管在实际上是否回得来还很难说。

这样的QR概念与传统雷达(CR)非常不同。在CR中因为是海量的光子而不谈论光子数目，只谈波束的功率和能量水平；而QR则是一种用少量光子完成雷达功能的装置。Lanzagorta在文献[27]§5.1.3中说：“quantum radar transmitter sends a single photon pulse towards a target，the target reflects the photon which is detected by the receiver”；这话的前句为“量子雷达发射机发送一个单光子脉冲射向目标”；但在另一处又说“with low number photon pulses”(使用较少数目的光子脉冲)；这是相互矛盾的说法。

总之，设计QR的一个基本问题是采用单光子发射还是采用多光子发射。另一个关键问题是运用纠缠态还是不运用纠缠态。真正的QR技术应为在微波的采用纠缠态的单光子雷达技术，困难之大无法形容，是对人类智慧的极大挑战。对于距离雷达站几百公里的目标，即使是量子散射，单个光子发射后回到雷达的几率非常小。因此，从概念和理论到制成QR样机，有很长的路要走。如使用纠缠光子对，据说雷达的分辨率和探测距离都会有较大提高。有一种看法认为，只有使用纠缠光子的技术才能充分保证量子雷达的优越性。对这一点，目前尚缺少实验证明。

很明显，如用微波作为工作频段，亦即设计“微波单光子雷达”，自然光源造成的干扰就可以避免。但是“微波光子”的能量、动质量都远小于“可见光光子”，所谓“微波光子雷达”的工程实现极为困难。

2018年5月10日美国刊物《国家利益》刊登一篇文章，题目是“量子雷达可以让F-22、F-35和歼-20无法隐身吗？”文章说，量子雷达通过利用晶体把一个光子分成两个纠缠光子，然后发射其中的一个光子，观察对其伙伴产生的相应效果。如果被发射的微粒撞到一架隐形战斗机，对该光子的影响就会在未被发射的伙伴光子上显现。那么显示“脉冲信号”的光子就会与未受影响的光子区分开来，构成一种雷达图像。这种武器不容易受到许多用于回避无线电波反射技术的影响，也不受干扰和其他电子战手段的影响。……不过这类说法都仅为一种概念，是否真如此还有待证明。

6月15日香港《南华早报》说：中国电子科技集团公司(CETC)两年前宣布，其科学家已经测试了有效范围为100km的量子雷达，理论上这种量子雷达能够侦测远距离的隐形战机。近日这家公司在南京举办的—个行业展会上表示，这项技术的新一代产品能探测高空飞行物(指弹道导弹、低轨卫星)，使用单光子探测技术；但又说“还在实验验证阶段”。

对于这些报道笔者是存疑的。—个基本问题仍然是，在白天空中有海量杂散光子，对QR发射的单光子脉冲阵列形成强干扰，那么QR是否能工作？……就有关QR的一些基本问题，笔者曾与专家讨论(参见附录Ⅱ)。

9 尚待研究的单光子现象

在光子学说的提出者A.Einstein于1955年去世后，光子的理论和应用均有很大进展，63年来成绩斐然。但在基础研究的层面仍有许多问题有待深入，这里仅举数例。

光子的非经典性可由量子力学中全同粒子不可分辨性原理出发而看出。全同性原理导致两个同类粒子交换后波函数不变，有这种对称性的粒子是Bose子，如光子和介子，自旋为整数值，不必满足Pauli不相容原理。这些都是经典物理学不曾考虑过的问题。总之，波动性、粒子性其实都来自经典物理观念，但现在不能再用经典物理来研究光子。例如，虽然辐射场可用简谐子来描写波动图像，但它属于量子化了的波动而非经典的波动。总之，对光子的一些奇怪现象(如同态光子干涉、单光子同时通过双缝、量子后选择等)，用传统的经典性、确定性(determinism)都无法解释。

1958年P.Dirac[42]在其著作《Quantum Mechanics》中提出了“光子自干涉”的论断，认为单光子只有自己发生干涉，从来不会发生不同光子间的干涉。但实验表明不同激光器发出的光子可以相干，这也说成是“光子自干涉”就说不通了。为克服这一困难，应将“光子自干涉”理解为包括同态光子干涉在内。光子即使来自不同的激光器，只要进入同一量子状态，就是不可区分的全同粒子，就能发生相干。实验表明正是如此，20世纪60年代L.Mandel领导的弱光干涉实验对此做了许多研究。

其次，应当对单光子从产生到消失的全过程作监测，笔者只知道—个实验例子。前已述及，2007年3月14日法新社从巴黎发出电讯称[43]：法国科学家发明了捕捉光子的装置，并且上百次成功地追踪到光子从产生到消失的过程。这实验生动有趣但也令人困惑——既然光子不是一个弹子球，“捕捉1个光子”是什么意思？如果说是“抓”到了1个光脉冲(人们只能经过它感知光子)，但光脉冲有3种可能，对光子的直观感受和认知仍未解决。其次，单光子存在时间只有半秒，那么人们又是如何能在QC中应用单光子呢？

最后，我们注意到这样的论文，它把讨论的内容核定在“有几万个光子”的情境中。例如2008年F.De Martini等[44]说，创造了一种单光子与多光子(有3.5×104个)系统相互纠缠的体系，实现了微观与宏观纠缠(两者相隔一个远距离)。实验中的宏观系统是用单光子量子比特(qubit)经光学参数放大器放大后得到的，故微观qubit和包含许多光子的宏观qubit之间相互关联且纠缠。……此文非常有创意，但也存在疑问——为什么实验者知道宏观系统中正好有35000个光子？显然这是估计的数据，因为如是计算或测量值就可能是(比如说)29937个或30015个，而不可能正好35000个。尽管如此，这种谈论“几万个光子”的论文仍然引起我们的注意；因为这是过去所不会有的。

对于单光子技术理论与应用的进一步发展，我们拭目以待。