基于SDAE的航空发动机燃油流量基线模型构建

黄 曦，卿新林 ，王奕首 ，殷 锴，赵 奇

（1.厦门大学航空航天学院，福建厦门361102；2.中国航发商用航空发动机有限责任公司，上海200241）

0 引言

航空发动机工作在高温、高压、高速等极端条件下，容易产生故障，致使飞机迫降停飞，甚至诱发飞行事故、危及飞行安全[1]。NASA的统计资料表明:在民用领域，发动机故障占所有飞机机械故障中的1/3。全世界每年花费的310亿美元维修费用中发动机日常维护占31%，翻修占27%[2]。为了在飞行过程中对航空发动机的健康状态实时监控，需要建立相应的参数基线。以往航空发动机的相关参数基线无法直接测量，一般由发动机生产商经过大量试验才能得到，属于发动机生产商的机密信息。随着大数据时代的到来，使用飞行数据建立基线模型的方法越来越普遍，需要根据基线值与实际值的偏差来判断发动机的运行状态，确定维修方案等。燃油流量是发动机重要参数之一，建立准确的燃油流量基线对于预防飞行事故的发生具有重要意义。

国内外的专家学者对于发动机重要参数基线模型开展了大量研究工作，取得了不少成果。朱睿和刘志荣[3]利用线性拟合建立发动机整体及风扇、压气机、高压涡轮和低压涡轮4个单元体性能的健康曲线，用于判断发动机整体及单元体的性能衰退情况；钟诗胜[4]采用基于核函数的多元非线性回归分析方法，对Rolls-Royce公司的发动机排气温度、燃油流量、高压转速和低压转速基线方程进行了求解；闫锋[5]设计了以高斯函数为隐含层激励函数、以线性函数为输出层激励函数的多输入单输出的RBF神经网络，建立了发动机燃油流量的健康基线来监测巡航过程中发动机状态参数的异常变化。但这些传统的算法普遍存在诊断精度不高、鲁棒性差等缺点。

目前常见的深度学习算法有自动编码器（Autoencoder，AE）[6]、深度置信网络（Deep Belief Network，DBN）[7]、卷积神经网络（Convolutional Neural Networks，CNN）[8]以及循环神经网络（Recurrent Neural Networks，RNN）[9]等。其中自编码器在图像识别[10]、语音识别[11]、自然语言处理[12]等领域已经广泛应用。堆叠降噪自动编码器（Stacked Denoising Autoen-coders，SDAE）算法由Vincent在2010年提出[13]，是在自动编码器和降噪自动编码器（Denoising Autoencoder，DAE）[14]基础上的改进算法，精度高、抗噪声能力强。为了克服传统机器学习算法在故障诊断领域的不足，本文采用SDAE建立了发动机的燃油流量的健康基线模型。

1 燃油流量基线模型构建

1.1 总体流程

自动编码器利用SDAE算法对燃油流量F建立基线模型的步骤如下:

（1）从真实的飞行数据中选取与F相关的参数作为输入；

（2）对初始数据进行预处理及其参数的修正；（3）将预处理的数据按照7∶3∶3的比例来构建训练集、验证集和测试集；

（4）将训练集输入到SDAE模型中，根据验证集结果调整SDAE模型的超参数；

（5）将测试集输入到近似最优的SDAE模型中，来确定模型的拟合精度；

（6）将预处理的数据加上随机高斯噪声，重复第（4）、（5）步骤，检验SDAE模型的抗噪声能力。

1.2 真实飞行数据的获取

试验数据选自某航空公司波音787客机的真实飞行数据，其部分参数的原始巡航数据见表1。

1.3 数据预处理及参数修正

考虑到飞行数据存在一些异常点和缺失点，建模前必须要对数据进行预处理。本文利用滑动中位数法对数据进行异常点去除，即建立1个滑动窗口，统计窗口内数据的中位数，若窗口内数据与中位数相差大于一定的阈值，则判定为异常点，对异常点和缺失数据点利用滑动窗口的均值补全。

表1 波音787客机部分飞行数据

在建模前需要将燃油流量、压力、温度和转速修正到标准大气压海平面状态下。在此引入温度修正因子θ和压力修正因子δ[15]

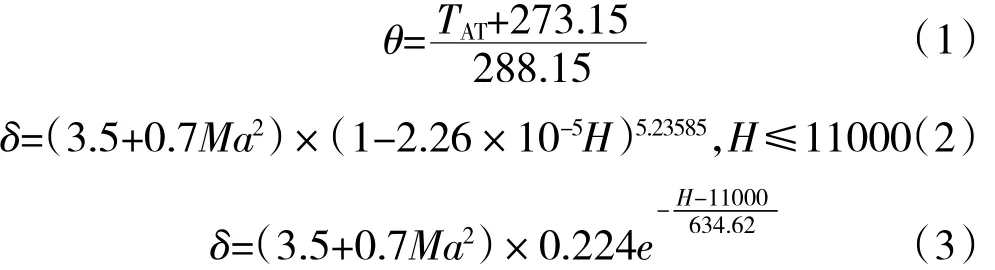
式中:H为飞行高度，根据θ和δ对参数进行修正。温度修正公式为

式中:Tcor为修正后温度；Traw为修正前温度。

压力修正公式为

式中:Pcor为修正后压力；Praw为修正前压力。

转速修正公式为

式中:Ncor为修正后转速；Nraw为修正前转速。

燃油流量修正公式为

式中:Fcor为修正后燃油流量；Fraw为修正前燃油流量。

1.4 堆叠降噪自动编码器

自动编码器（Auto-Encoder，AE）是深度学习网络中常见的基础结构，是1种无监督的学习算法，主要用于学习输入数据集压缩的抽象表达。基本的AE由1个3层神经网络构成:1个输入层，1个隐藏层和1个输出层，如图1所示。由输入层（L1）到隐藏层（L2）的过程称为编码阶段，由隐藏层（L2）到输出层（L3）的过程称为解码阶段。

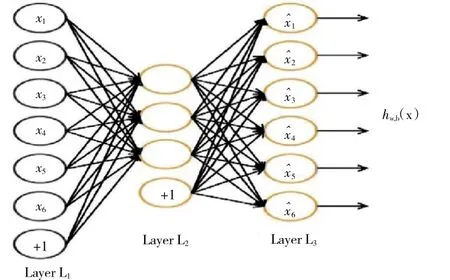
图1 AE网络结构

令f和g分别代表编码函数与解码函数。则有

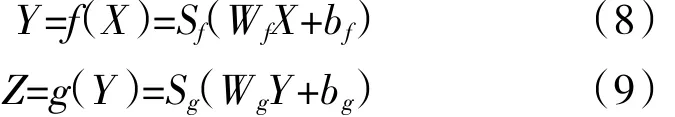
式中:Sf、Sg分别代表编码器和解码器的激活函；Wf为编码权重矩阵；Wg为解码权重矩阵；bf、bg分别为编码器和解码器偏置向量。一般选择sigmoid函数

且权重矩阵Wg通常取自编码网络的作用是将输入样本X压缩到隐藏层Y，再在输出端Z重建样本。其目标是使输出和输入之间误差尽量小。一般使用平方误差

作为自动编码器的损失函数。式中:d为输入和输出的维度。

对于样本容量为N的训练样本，自动编码器的风险函数为

最后通过随机梯度下降算法最小化J（θ），求出参数空间θ。

DAE是在自动编码器的基础上为了防止过拟合问题而对输入的数据（网络的输入层）加入噪声，使学习得到的编码器具有较强的鲁棒性，从而增强模型的泛化能力，其结构如图2所示。对输入数据加入噪声的方法，一般为加入与输入数据同分布的高斯噪声，或以一定概率将输入向量的分量置0。

图2 DAE结构

SDAE是多个降噪自动编码器堆叠组成的1种深度网络结构，利用前1层编码器的输出作为当前层编码器的输入。为了解决深度网络训练过程中出现的梯度消失等问题，Hinton基于深度置信网络提出了1种贪婪逐层训练算法，即每次只训练1层网络，然后再将训练好的网络固定去训练下1层[16]，如图3所示。通过第1层DAE的学习得到的编码输出，再以此输出通过相同的方法添加噪声进行训练得到第2层的编码输出，最后根据需要重复此过程。

图3 SDAE结构

通过无监督训练得到的SDAE只是得到的原始数据精炼、抽象的1种表达，称为整个基线模型的预训练阶段，还不具备对基线的拟合能力。要想建立准确的健康基线，一般需要在SDAE顶端再添加1个回归层（如线性回归层），并结合少量有标注的训练数据在损失函数的指导下对系统的参数进行微调，使得整个网络能够完成对发动机燃油流量基线的建立。

2 试验及结果分析

2.1 模型建立

试验共选取1300组数据用于建立基线模型，其中700组用作模型的训练集，300组用作模型的验证集，300组用作模型的测试集。令

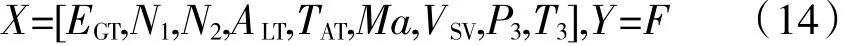
利用深度学习开源框架Keras构建BP（Back Propa-gation）神经网络和SDAE模型。针对2种模型分别选取一些不同的网络结构进行训练，记录验证集的均方误差（Mean Squared Error，MSE）随着迭代次数的变化，从而确定较优的网络结构和迭代次数。其中BP分别选取网络结构为 （9，10，1）、（9，15，1）、（9，20，1）、（9，10，10，1）、（9，15，15，1）、（9，10，20，1）进行验证。验证结果如图4所示。从图中可见，当BP网络结构为（9，10，1），迭代次数为750次时，验证集的MSE最小。

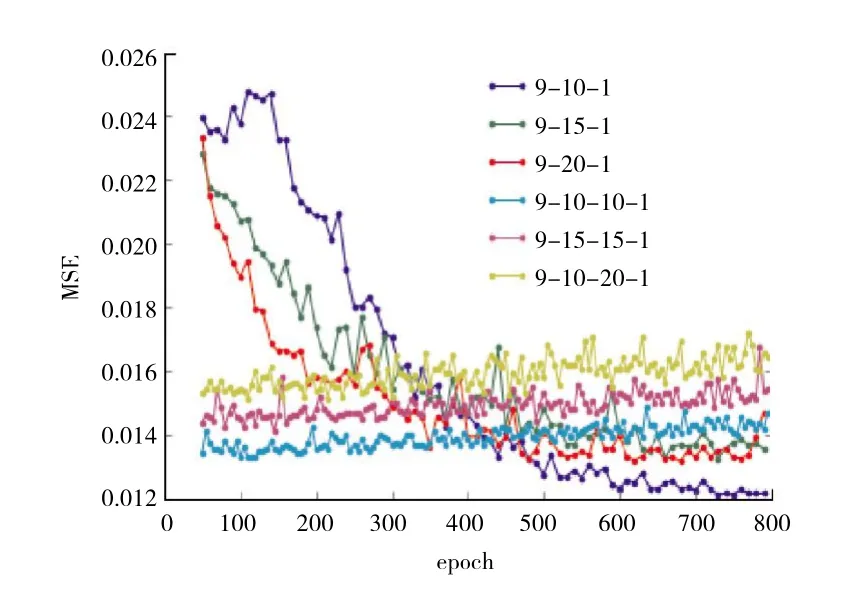
图4 BP模型验证集的MSE

同理，分别选取结构为（9，10，5，1）、（9，10，7，1）、（9，7，4，1）、（9，8，5，1）的 SDAE 模型进行验证，其结果如图 5所示。当 SDAE 模型结构为（9，10，7，1），迭代次数为250次时，验证集的MSE最小。

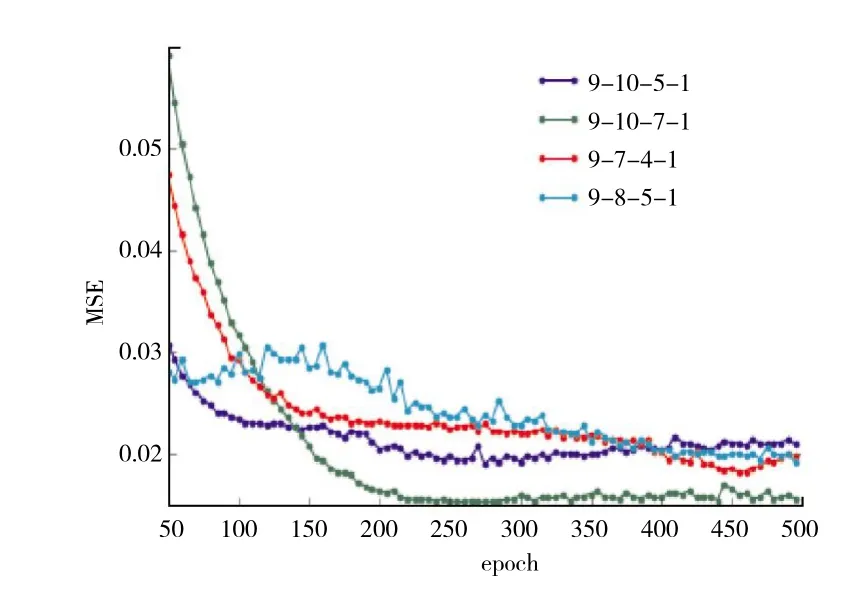
图5 SDAE模型验证集的MSE

2.2 模型结果对比

对训练好的近似最优的BP模型和SDAE模型在测试集上的MSE比较可知，BP的MSE为0.023，而SDAE的MSE为0.017。基于BP模型和SDAE模型的燃油流量预测曲线分别如图6、7所示。从图中可见，SDAE模型在波动聚集区间的预测效果明显优于BP模型的。

BP模型和SDAE模型的预测误差百分比分别如图8、9所示。从图中可见，SDAE模型的预测误差百分比小于BP模型的。

图6 基于BP模型的燃油流量预测曲线

图7 基于SDAE模型的燃油流量预测曲线

图8 BP模型预测误差百分比

图9 SDAE模型预测误差百分比

实际飞行数据中不可避免地存在噪声，需要评估所建立模型的抗噪声能力。本文对输入数据加入不同等级的高斯噪声，比较BP模型和SDAE模型在不同噪声等级下的拟合精度。2种模型抗噪声能力的比较如图10所示。从图中可见，随着噪声等级的增加，2种模型的MSE都在上升，但是SDAE模型的MSE上升的趋势相对更平缓，因此判断SDAE模型比BP模型有更好的抗噪声能力。

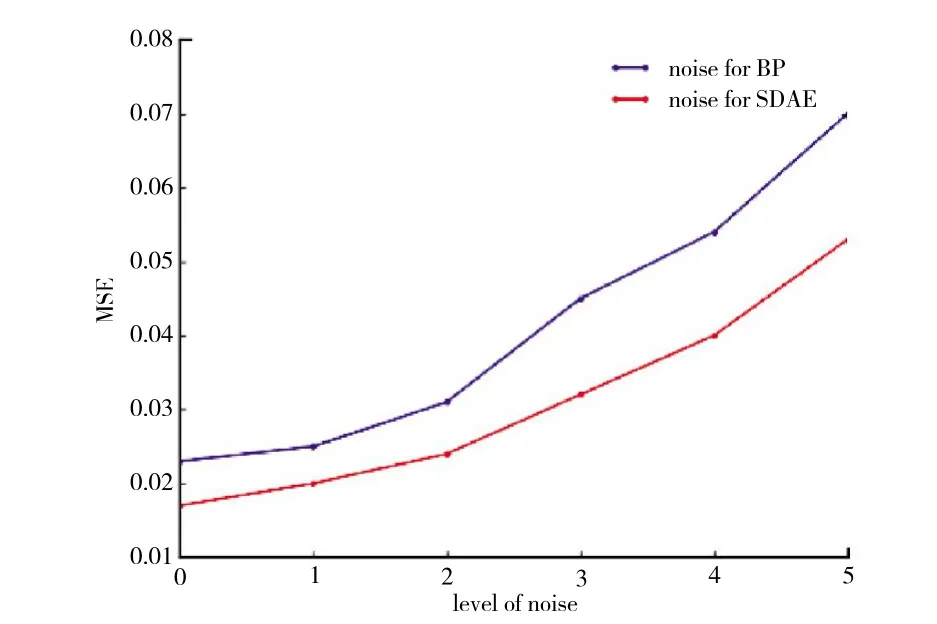
图10 BP模型和SDAE模型抗噪声能力比较

3 结束语

本文首次将深度学习算法中的堆叠降噪自编码用于发动机燃油流量基线模型的构建。利用真实民航飞行数据对模型进行验证，并将其与传统的BP神经网络算法在基线建立精度和抗噪声能力上进行比较。试验结果表明，基于SDAE的航空发动机燃油流量基线模型的精度和抗噪能力都优于基于BP算法的基线模型的。