热载荷对止口连接结构过盈量的影响分析

杨 阳 ，罗 忠 ，刘永泉

（1.东北大学航空动力装备振动及控制教育部重点实验室，沈阳110819；2.中国航发沈阳发动机研究所，沈阳110015）

0 引言

在航空发动机中，止口连接结构早期与螺栓连接等其他连接方式配合使用，近几年开始独立作为连接结构应用，该结构在实现定心传扭的同时，大大减少了连接结构零件数量，有效减轻了发动机质量，很好地顺应了现代航空发动机高转速、轻质量的发展方向[1-2]。例如20世纪90年代GE公司在燃气轮机高压转子中设计了带有拉杆系统的止口连接结构[3]；德国的MTU公司设计的1种无螺栓高压压气机转子中利用止口连接代替了螺栓连接[4]；美国PW公司的PW1000G齿轮传动涡轮风扇发动机高压转子中也采用止口连接结构[5]。为保证止口界面工作时不发生径向分离和周向相对位置的变化，止口连接结构的内外圆柱面需要采用过盈配合。然而在航空发动机工作过程中，高转速和复杂温度场会使止口连接结构的过盈量发生明显变化，如何保证变化后的止口连接结构仍然具有稳健的连接能力成为航空发动机连接结构领域的重要研究内容之一。

国内学者杨帆等[6]介绍了1种新式无螺栓高压压气机结构，采用止口连接结构代替了以往的长螺栓连接结构，指出在较大的离心载荷和热载荷作用下，止口连接紧度如果选取不当会有松脱的危险；岳伟等[7]通过对止口连接结构进行受力和止口连接稳健性的影响因素分析，认为止口结构会在多种载荷作用下发生不协调变形，使得初始装配时的结合面过盈量发生变化，从而影响止口的连接能力；范潘潘等[8]分析了离心载荷对涡桨发动机压气机轮盘止口连接结构配合面过盈量的影响，推导出轮盘止口过盈量与扭矩、转速之间的关系，提出1种止口连接过盈量的估算方法。国外学者Werner Mack[9]指出，过盈连接件之间的传扭能力会因为塑性变形和热膨胀而使永久性降低，从而使连接失效；Á Kovács[10]利用半解析的方法分析了过盈配合结合面间在非均匀、稳态温度分布下的应力状态，表明温度梯度的存在使结合面应力明显增大。

从目前已有的研究成果可知，除离心载荷外，热载荷也会对过盈配合结合面状态产生较大影响[11-12]，如果设计不合理，止口连接结构可能会因较大的温差变化而出现滑动甚至松脱，从而导致连接失效。本文基于热弹性力学理论推导止口连接结构径向热变形与温度变化的关系，参考航空发动机工作时的温度场状态计算相应状态下的止口过盈量，并与不考虑温度场时计算出的过盈量进行对比。

1 止口连接结构应力应变分析

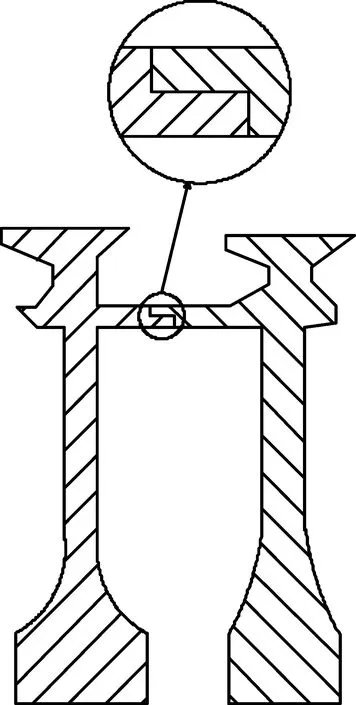
图1 止口连接结构

止口连接结构多用于压气机各级轮盘间的连接。位于2盘之间的鼓筒部分的止口连接结构如图1所示。止口连接结构通过端面受轴向力压紧，圆柱面过盈配合实现传扭。航空发动机在高速旋转时，涡轮前温度较高，常常需要从压气机引入冷却空气对其进行冷却[13]。冷却气流从盘心流过，而轮缘处位于主流高温度区域，盘缘与盘腔的温度差使得压气机轮盘径向温度分布不尽相同[14-15]，使位于各盘之间的止口连接结构在径向上产生不协调变形，使配合面间的过盈量发生变化，从而影响连接结构的稳健性。

1.1 力学模型

为研究热载荷下止口连接结构径向变形对过盈量的影响，将止口连接结构简化为套装圆筒模型，如图2所示。该结构由内、外2个圆筒通过过盈配合套装组成，在结合面处因为过盈量的存在而受到均匀分布的压力p作用。内筒的内径为a，外径为b，外筒的内径为b，外径为c，内、外筒采用相同材料，弹性模量为E，泊松比为v，用ρ表示圆筒截面上任意半径。

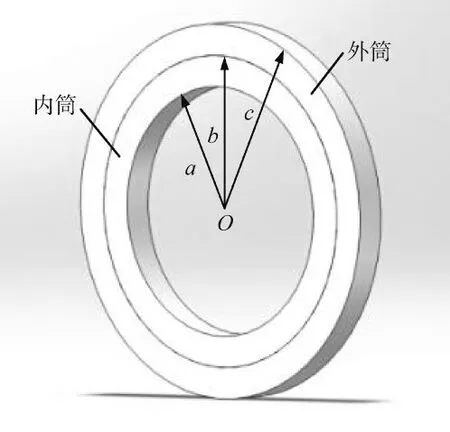
图2 止口连接结构模型

1.2 应力应变分析

为简化分析，首先作如下假设:

（1）模型处于轴对称平面应力状态；

（2）模型的变形始终处于弹性范围内。

基于以上假设，应力应变函数只是径向坐标ρ的函数，且切向力 τρθ=0，τφρ=0。根据热弹性力学列出极坐标下的不考虑体力的平面应力平衡微分方程、几何方程和物理方程[16]

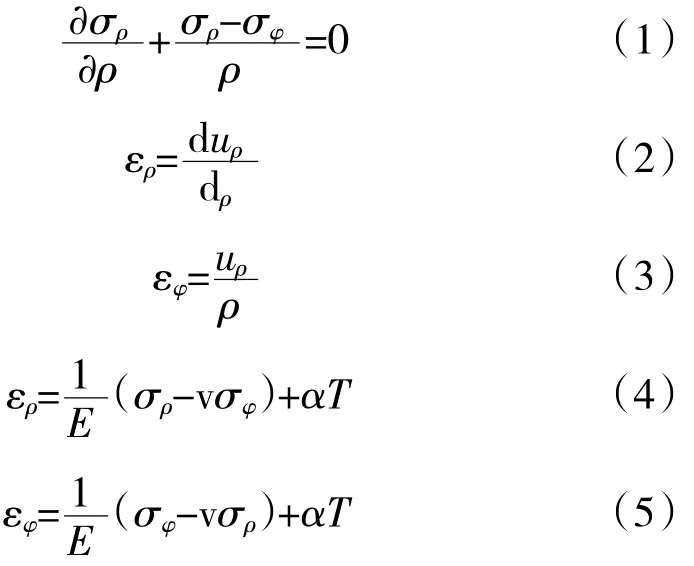
式中:σρ、σφ分别为极坐标下径向和周向正应力；uρ为径向位移；ερ、εφ分别为径向、周向应变；α为线热胀系数；αT为在变温T下弹性体内部各点微小长度发生的应变。

联立式（1）～（5），得到按位移求解轴对称热应力的基本方程

对式（6）左侧进行积分，积分下限取内筒内径a，得到内筒位移分量

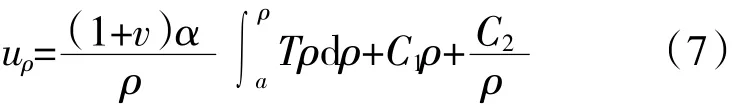
式中:C1、C2为任意常数。

利用式（7）可得内筒任意位置处径向应力

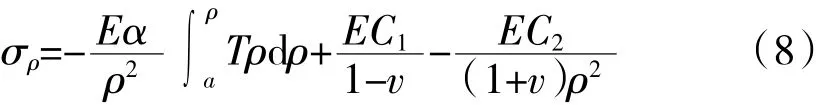
首先针对内筒进行分析，其外表面为配合面，因过盈配合受到均布压力p，内表面为自由面，故边界条件为

将边界条件式（9）带入式（8）中，并将求解出的C1和C2带入式（7），得到内筒在该情况下不同半径处的位移变化量

将内筒径向任意位置处的变形量分解成2部分，其中uT1为温度场下内筒径向发生的温度变形，uf1为在边界条件下内筒径向各点处产生的初始变形。

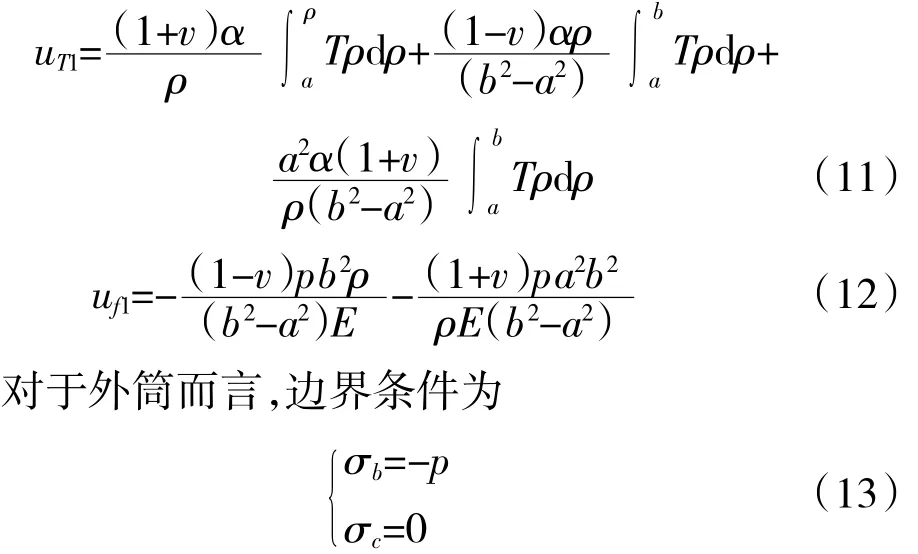
与计算内筒位移表达式类似，利用边界条件式（13）可以确定常数C1和C2，带入式（7）中可确定外筒在该边界条件下的位移

同样，该位移表达式也可以分解为2部分。uT2是由于温度场的存在而使外筒产生的温度变形，uf2是在边界条件式（13）下外筒径向不同位置产生的初始变形。

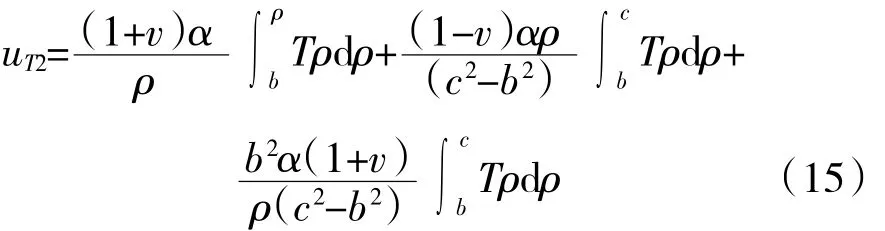
1.3 止口模型结合面过盈量计算方法

若不考虑不均匀热载荷的影响，传递一定扭矩的过盈连接可以参考国家推荐标准中的一般过盈配合有效过盈量计算方法进行设计[17]

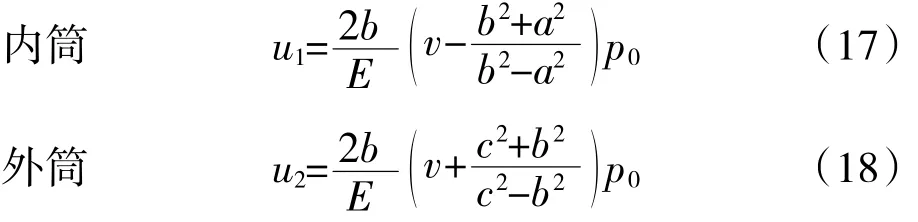
即当总过盈量为u=2（u2-u1）时，过盈配合结合面会产生大小为p0的结合压力，以实现扭矩的传递。然而这种计算方法并不适用于处在不均匀温度场下的过盈连接结构。

根据上述推导结果，假设止口连接结构处于无变温理想环境下，此时位移表达式（10）、（14）中的 T=0，内筒产生的变形为2uf1，外筒产生的变形为2uf2，化简后结果与国家推荐标准中的过盈量计算式相同。

当内、外筒的结合面之间无接触压力而仅存在温度场时，内、外筒相对变形量 us=2（uT2-uT1）。当 uT2＞uT1时，us为正，内、外筒之间产生间隙；反之，us为负，内、外筒之间产生过盈。

通过式（17）、（18）计算出的过盈量在均衡温度场状态下确实提供了足够的结合面压力，但是当受到不均衡温度场的影响时，接触状态会发生变化，结合压力也就不再是设计时所要求的值。在设计过盈连接时，应当考虑在工作状态下连接件受温度场的影响而产生的变形，即要保证结合面产生大小为p的结合压力时，过盈量应为

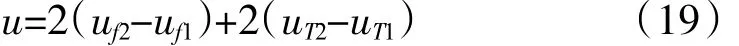
2 止口连接结构过盈量计算

2.1 算例模型

利用上述推导结果，针对具体算例进行计算，并对结果进行分析。模型参数见表1。

表1 算例模型参数

2.2 温度场的建立

为模拟航空发动机工作的环境，参考文献[13]中计算得到的压气机温度场情况，设定内筒内表面温度为170℃，外筒外表面温度为220℃，因为内、外止口厚度尺寸相对较小且为同种材料，所以在建立温度场时可以认为温度是线性变化的。由此可求出径向不同位置与温度值的关系，如图3所示。图中0.05 m位置处的温度为195℃，可认为是止口界面处的温度值。

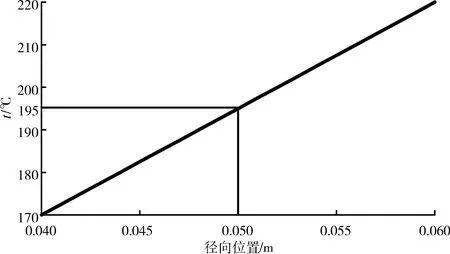
图3 温度与径向位置关系

2.3 过盈量计算

根据所建立的温度场和推导出的初始位移表达式（12）和式（16）、热载荷下温度位移表达式（11）和式（15）进行计算，结果如图4、5所示。

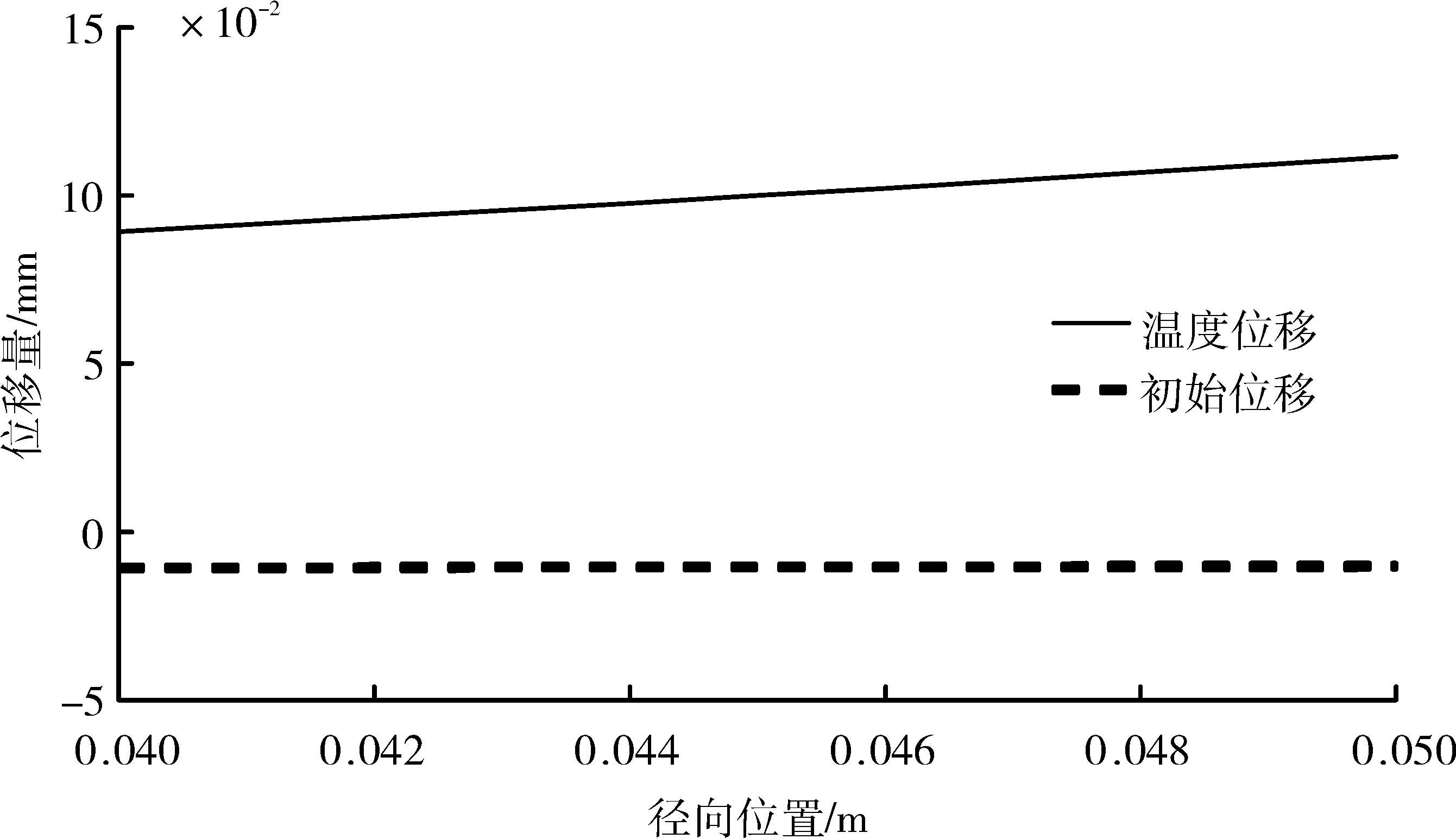
图4 内筒不同位置位移变化

图5 外筒不同位置位移变化

从图中可见，因温度而产生的位移随半径的增大而增大，初始位移随半径略有变化，但并不明显。为方便计算，提取半径为0.05 m处的内、外筒半径变形量，见表2。

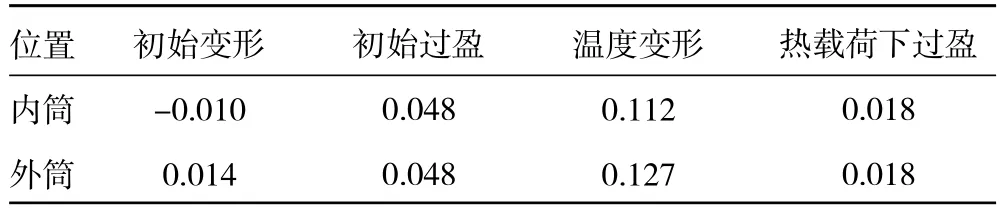
表2 结合面处内、外筒位移量 mm

从表中可见，初始过盈量为外筒半径初始变形减去内筒半径初始变形的2倍，即0.048 mm，当加载温度载荷时，内筒半径向外膨胀了0.112 mm，外筒半径向外膨胀了0.127 mm，2筒半径的相对位移变化量为0.015 mm，即热载荷条件下过盈量变为0.018 mm，过盈量减小了63%。由此可见，温度载荷的存在使得止口过盈配合面间的过盈量发生了较大变化。

计算结果表明，如果要使不均匀温度场下过盈配合结合面之间仍能产生足够的结合压力，设计的过盈量不仅要保证初始过盈量，还要补偿因为温度场造成的不协调变形。所以本算例设计变形量应按式（19）计算，结果为0.078 mm。

3 仿真验证

为了验证上述推导结果的有效性，利用有限元软件进行仿真对比，主要包括温度场的稳态热分析仿真以及变形量仿真。

3.1 热分析仿真

利用有限元仿真软件的稳态热分析模块，采用与第2.2节中相同的温度边界条件，仿真得到内、外筒模型的温度场。

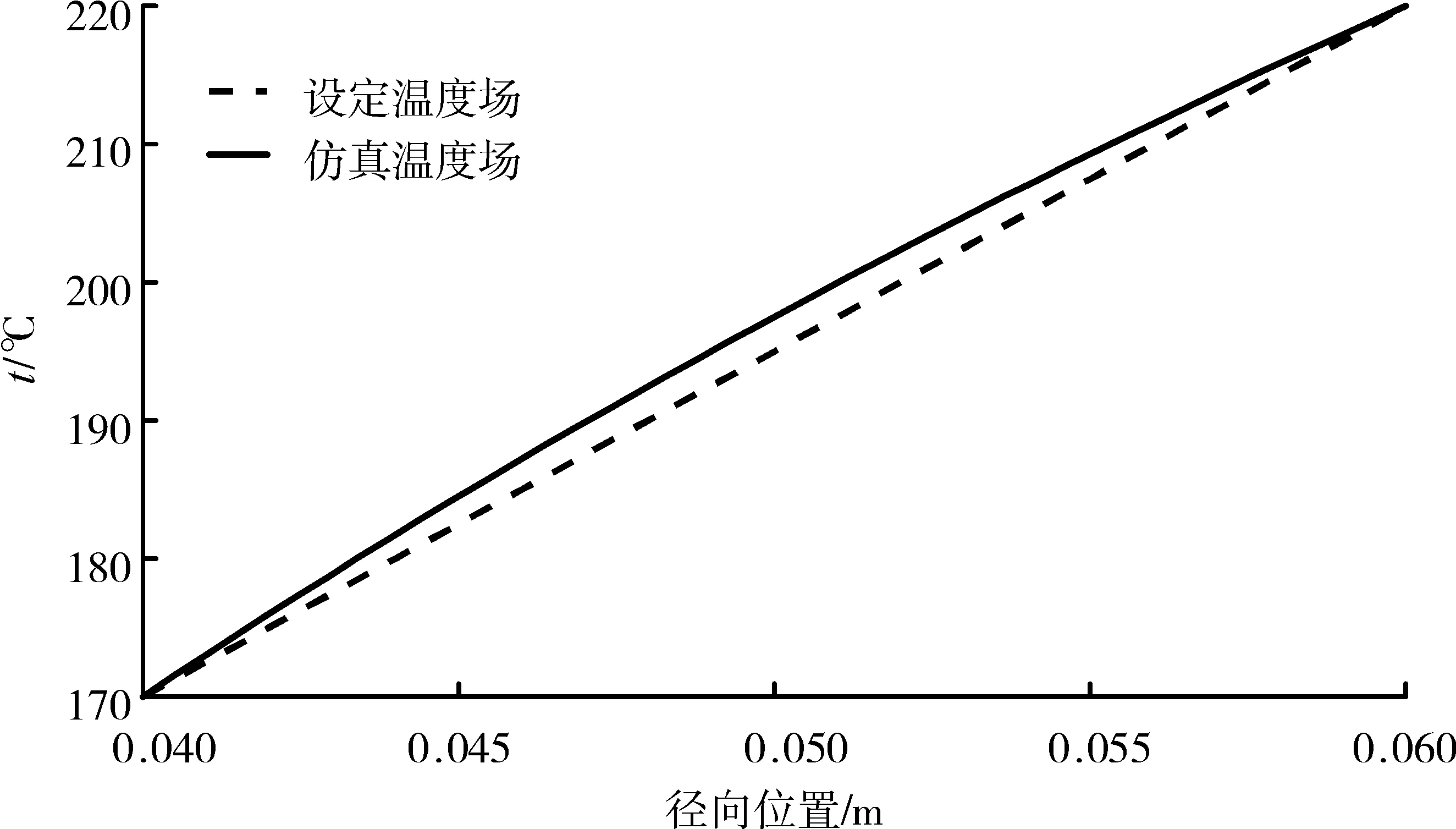
图6 温度场对比

首先建立实体模型，采用多域扫掠方法划分网格，单元类型为Solid186，共划分2700个节点，300个单元。过盈量设置为初始过盈量0.049 mm，内筒内表面温度设置为170℃，外筒外表面温度设置为220℃，为了便于对比，将前文中设定的温度场与仿真得到的温度场绘制于同一图中，如图6所示。从图中可见，2条线基本重合，偏差最大的位置温度值相差2℃，设定温度场与仿真温度场相比最大相对误差为1%，故可认为设定温度场能够代替真实温度场。

3.2 变形量仿真

在稳态热分析的基础上，对内、外筒进行变形量仿真，包括热载荷条件下的热变形仿真和静力学条件下的初始过盈量的仿真。

首先建立内筒的3维模型，导入有限元分析软件中，采用扫掠方法划分网格，单元类型为solid186，共得到1800个节点，240个单元。热分析过程与上文中温度场仿真过程类似，此处设置内、外表面温度分别为170℃、195℃。在热分析结束之后，添加静力分析模块，约束端面除径向自由度外的所有自由度，提取内筒径向变形情况，与前文中理论计算得到的结果绘制于同一图中，如图7所示。利用静力学模块进行初始过盈量仿真，在内筒外表面施加10 MPa的压力。初始位移的仿真值与理论计算值对比如图8所示。

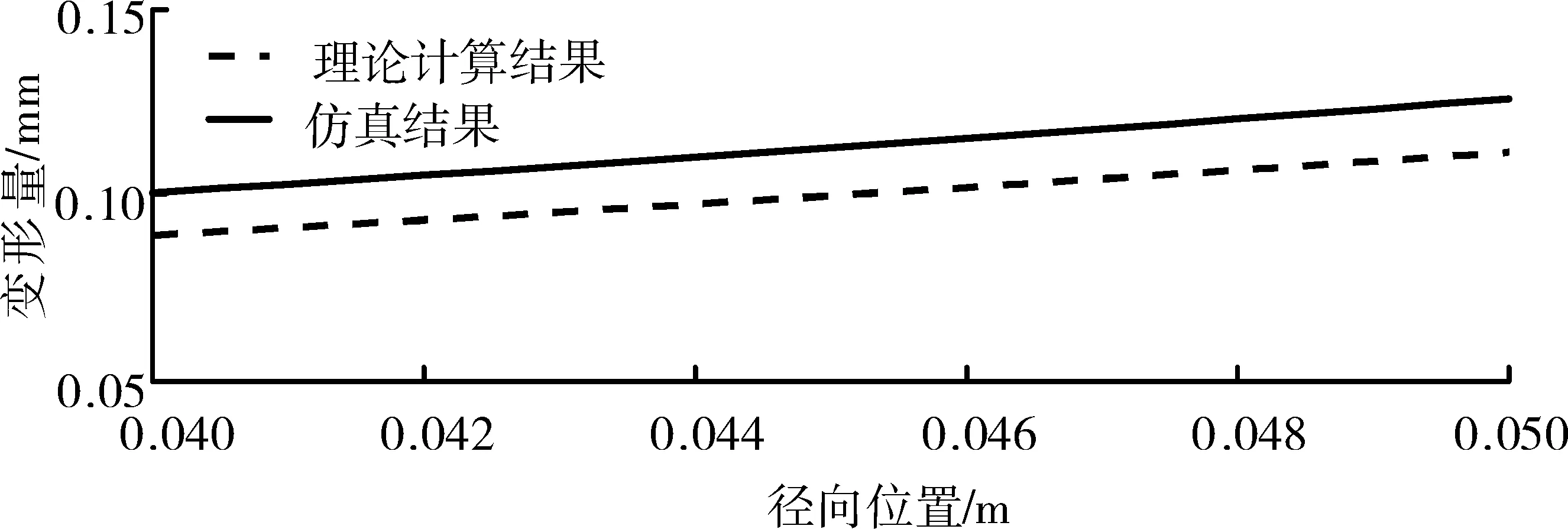
图7 内筒热变形理论与仿真结果对比

图8 内筒初始位移理论与仿真对比

接下来建立外筒3维模型，网格划分方法与内筒的相同。热分析时设置内、外表面温度分别为195℃、220℃。在热分析结束之后，添加静力分析模块，约束端面除径向自由度外的所有自由度。为方便对比，将外筒热变形仿真结果和理论计算结果绘于同一图中，如图9所示。

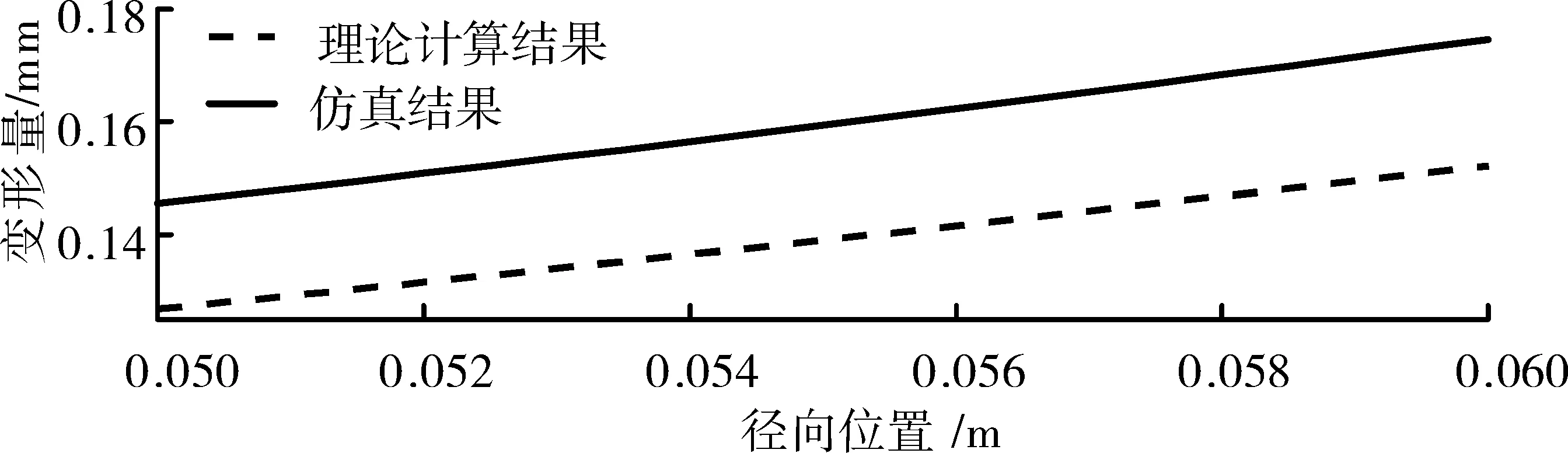
图9 外筒热变形理论与仿真结果对比

对外筒进行初始位移仿真，与内筒的类似，只需在静力分析模块中给外筒内表面施加10 MPa的法向压力，并限制2端面除径向外的所有自由度，为方便对比，将仿真结果与理论值绘制于同一图中，如图10所示。

图10 外筒初始变形理论与仿真结果对比

3.3 结果分析

提取内、外筒仿真结果中结合面处的变形量，与理论计算值进行对比分析，见表3。

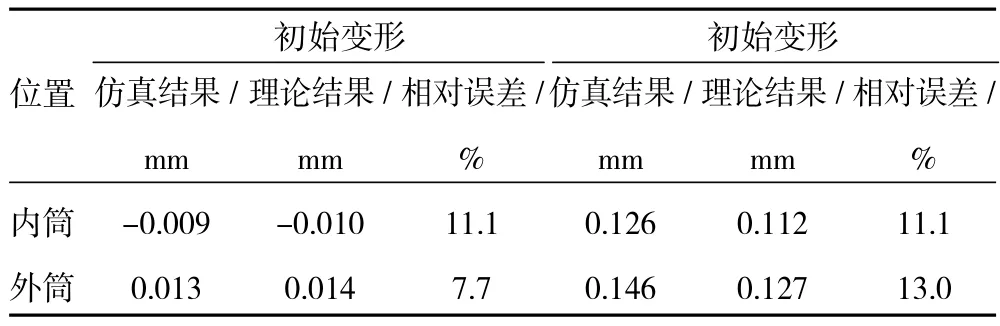
表3 内外筒变形量对比

利用式（11）、（12）、（15）、（16）、和（19）并结合表3中的数据可计算出设计过盈量及过盈量损失情况，见表4。

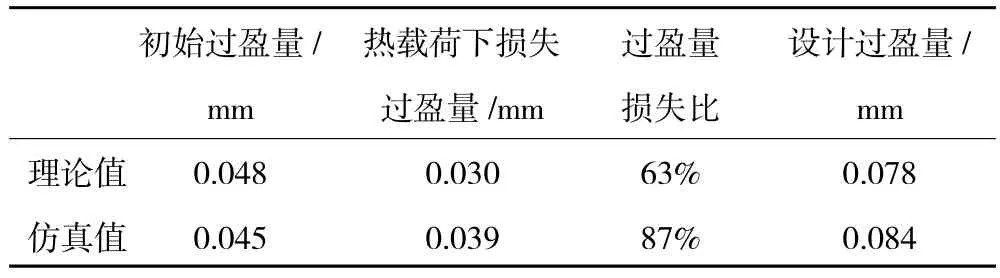
表4 过盈量对比

造成变形量的理论结果与仿真结果之间误差的原因主要有:

（1）理论推导过程中出于简化的目的，认为温度场是线性变化的；

（2）推导时将该问题简化为平面问题。

由于这2方面因素导致了误差的存在，但是相对误差不超过13%，仍处于可接受范围内。

从表4中可见，理论计算表明损失过盈量占原初始过盈量的63%，仿真结果为87%，二者之间的差别主要是由于上述2点原因造成的误差的积累。热载荷的存在使得止口连接结构过盈量出现了明显损失，实际过盈量大幅度减小使得止口连接结构在工作过程中的传扭能力明显降低，在过盈量设计时应加以补偿。通过理论计算得到的设计过盈量应为0.078 mm，利用仿真数据计算得到的设计过盈量为0.084 mm，二者相对误差为7.1%，具有较好的一致性。

4 结论

本文通过理论推导与算例计算，结合有限元仿真，提出了1种考虑热载荷的止口结构过盈量计算方法，并得出以下结论:

（1）不均匀温度场的存在会使止口连接结构的过盈量发生明显变化，特别是在航空发动机工作时的温度场条件下，过盈量会出现明显损失。在设计阶段选取过盈量时，应当对损失的过盈量进行补偿；

（2）通过有限元仿真对比，证明本文采用的计算热载荷条件下过盈量变化方法较为准确，更加贴近止口连接结构的真实工况，可以为航空发动机止口结构设计提供参考；

本文只考虑了热载荷对止口结构径向变形的影响，而在实际工况下，因热载荷而产生的轴向变形对止口连接结构的影响也不容忽视，有待进一步研究。