机匣螺栓连接分区域薄层单元建模方法

王 攀，臧朝平

（南京航空航天大学能源与动力学院，南京210016）

0 引言

螺栓连接结构凭借构造简单、实用性强等优点，被广泛应用于航空发动机机匣和转子结构的连接。在工程应用中，螺栓连接件在承受工作载荷之前，需要对螺栓施加一定的预紧力，使螺栓和被连接件之间产生相互作用力，从而产生不同的接触面连接刚度，进而影响结构的动力学响应。因此，螺栓连接结构建模方法的研究成为结构动力学研究领域的热点问题[1]。螺栓连接的有限元模拟方法主要分为2类:非线性接触算法和界面单元法。前者需要迭代计算结构响应，计算量较大。随着有限元法的发展，Liu等[2-3]建立了螺栓连接部件的精细有限元模型，但由于其自由度数目庞大，不适用于复杂的连接结构；Ahmadian等[4-6]运用薄层单元法将连接结构接触面等效为厚度很薄的实体单元，进行动力学建模，并运用优化算法修正薄层单元材料参数；马双超等[7]将薄层单元法运用到航空发动机领域；姚星宇等[8-9]给出薄层单元法在航空发动机机匣螺栓连接结构的建模原理，并研究了薄层单元材料参数对螺栓连接刚度的影响规律，但文献中并未考虑由于施加不同的预载荷使螺栓法兰连接结构实际接触面积变化，以及接触微凸体变形带来的刚度改变影响整个装配体的动力学响应。

本文基于螺栓连接结构的超模型连接刚度计算公式[10-12]，运用赫兹接触理论以及M-B分形模型[13-16]，推导了不同预紧力螺栓连接简化模型连接参数的计算公式，并以1个螺栓连接试验机匣为例，对该简化模型的仿真频率与模态试验测试频率进行对比。

1 分区域薄层单元建模方法

1.1 分区域薄层单元

采用分区域薄层单元对螺栓连接部分进行简化建模，如图1所示。图中绿色部分代表预紧力影响较弱的法兰区域；红色部分代表预紧力主要影响的螺栓区域。

图1 分区域薄层单元简化模型

把上安装法兰1、薄层单元2和下安装法兰3视为串联的弹簧结构，可得薄层单元连接结构的轴向总刚度

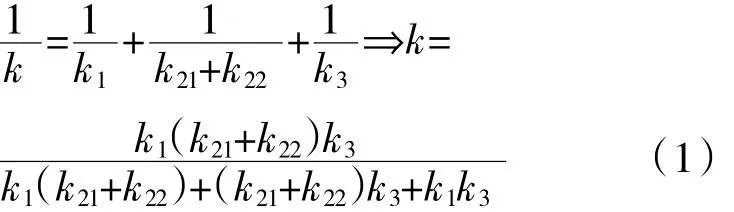
式中:k1、k21+k22和k3分别为上安装法兰、薄层单元和下安装法兰的轴向刚度；k21和k22分别为图1中红色部分薄层和绿色部分薄层的轴向刚度。

分区域薄层单元部分的轴向总刚度为

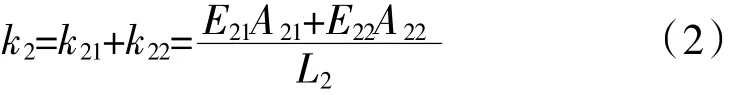
式中:E21和E22分别为图中红色区域和绿色区域的弹性模量；A21和A22分别为图中红色部分和绿色部分的面积；L2为薄层的厚度。

1.2 薄层单元轴向总刚度

对螺栓连接结构件进行静力学分析，连接区域的应力分布集中在螺栓杆、螺母与被连接件接触的区域，如图2所示。其中螺栓连接结构的轴向连接刚度主要由螺杆连接的区域与预紧力作用的区域决定[8-9]。

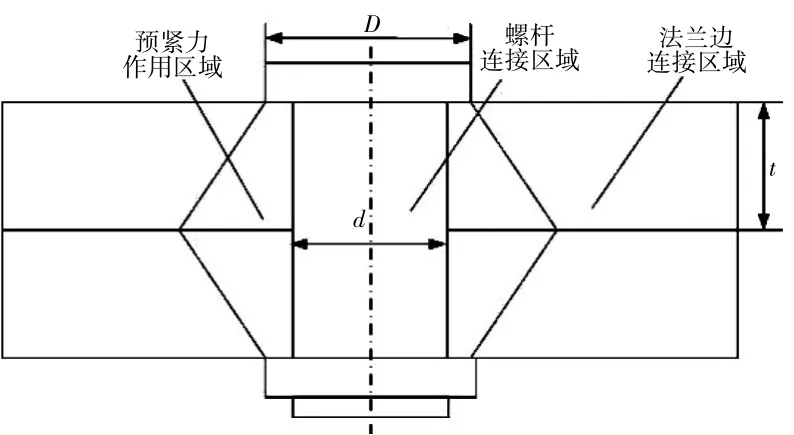
图2 螺栓连接结构区域

螺杆连接区域的轴向刚度为

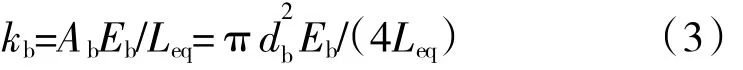
式中:Ab为螺栓杆的截面面积；db为螺栓杆的直径；Eb为螺杆弹性模量；Leq为螺栓杆的当量长度。

对于螺栓预紧力作用区域，将被连接件的预紧力分布区域等效为切去顶端的锥形区域。可得该区域的连接刚度为

式中:E0i为被连接件的弹性模量；t为法兰边厚度；α为半锥形角，与螺栓预紧力F大小有关。

由于整个螺栓预紧力作用区域中，上下2个被连接件为串联关系，则可知该区域的轴向连接刚度为

由此可得整个螺栓连接区域的连接总刚度ks

1.3 法兰区域刚度

1.3.1 赫兹接触理论

法兰接触面实质上由2个粗糙表面组成，粗糙表面的微凸体在外载荷作用下发生变形，如图3所示。根据赫兹公式[13-14]可得微凸体法向载荷和弹性变形的关系

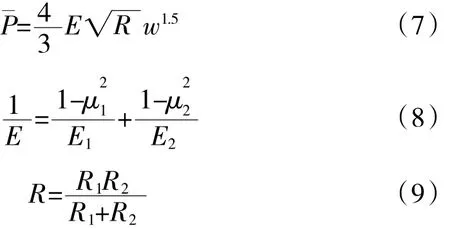
式中:E为2个接触面的等效弹性模量；R为2个微凸体的等效接触半径；w为接触点的法向变形量。微凸体接触区域的接触面积可以表示为a'=2πRw。

轴向载荷P对法向位移w求导，求解出微小接触点的刚度为

具有截面积的微凸体的变形[13-14]为

将式（11）带入 a′=2πRw，可得微接触点顶端的曲率半径

通过对大量试验数据进行拟合[15]，可得金属表面机械加工后的分形维数D、特征尺寸系数G与加工表面粗糙度Ra之间的关系式分别为

图3 法向外载荷作用下的微凸体变形

1.3.2 M-B分形模型

粗糙表面中微凸体的近似分布形式如图4所示。根据M-B分形模型[13-14]，微凸体截面积为a′的接触点大小分布函数 n（a′）为

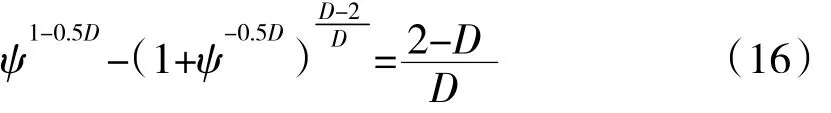
式中:ψ为加权系数

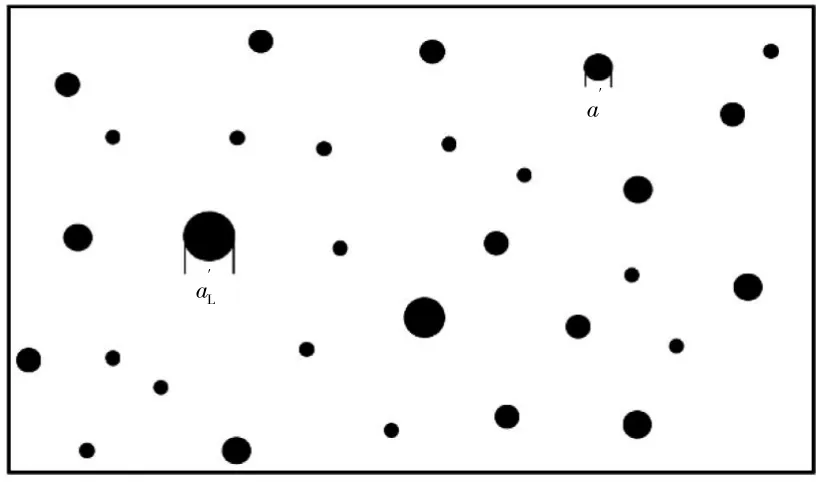
图4 接触表面微凸体分布

在接触面处，区分弹塑性变形临界面积a'c为

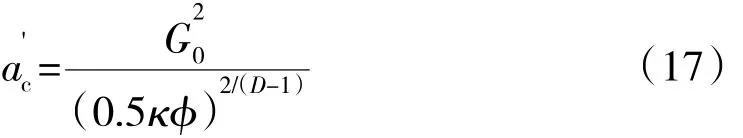
式中:κ=H/σs；Φ=σs/E；H 为较软材料的硬度；σs为较软材料的屈服强度。

微凸体的法向塑性形变载荷与接触面积关系为

综上所述，赫兹公式描述的单个微凸体的接触刚度、M-B分形接触模型以及结合面的法向接触刚度，可由单个接触点的刚度式（10）根据尺寸分布n（a'）积分得到

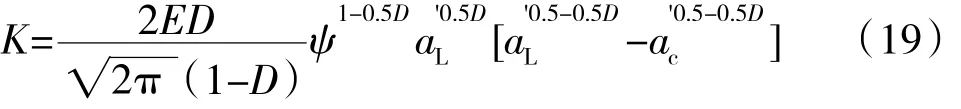
将式（11）（12）、带入式（7），加上塑性形变载荷（18），根据尺寸分布积分，得到结合面的法向弹塑性总载荷

1.4 分区域薄层单元弹性模量

根据工程经验，对于螺杆直径为d的螺栓，拧紧力矩M和预紧力F之间相互换算的经验公式为

法兰的法向总载荷P即为所有螺栓的总预紧力，从而确定法兰法向接触刚度K作为分区域薄层单元中的法兰区域刚度。再由螺栓连接部分的总刚度ks确定出螺栓区域刚度。之后，结合式（23）和式（24）可以求解出分区域薄层单元的弹性模量

2 螺栓连接机匣试验

2.1 机匣静力学分析

对于如图5（a）所示的螺栓连接机匣，由36个M6螺栓连接。根据超模型的建模方法，采用实体螺栓结构建立机匣连接件的超模型。为了后续的静力学分析，确定半锥形角。设定超模型网格尺寸为3 mm，采用2阶4面体单元划分网格，如图5（b）所示。该连接模型共有148万个节点，444万个自由度。

图5 连接机匣

在连接螺栓上分别施加 3、5、7、9、11 N·m 的预紧力，确定半锥形角，根据式（6）计算总刚度ks，见表1。

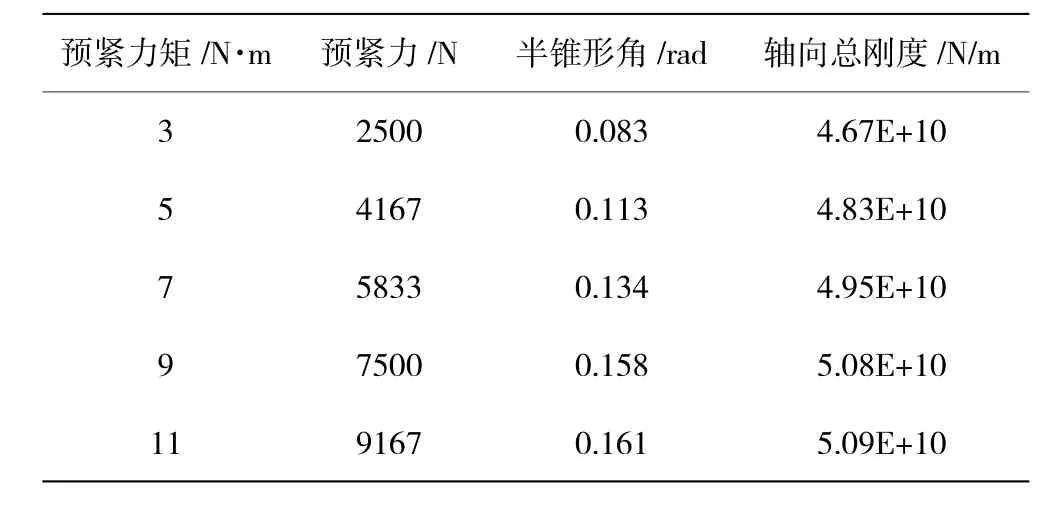
表1 不同预紧力下机匣连接件轴向总刚度

不同拧紧力矩下机匣连接件总刚度的变化如图6所示。从图中可见，轴向连接刚度曲线的斜率随着拧紧力矩的增大逐渐减小，说明随着拧紧力矩的增大，机匣螺栓法兰连接部分逐渐趋于刚性。

2.2 螺栓连接机匣简化

根据分区域薄层单元建模方法，去除机匣连接件法兰边上的螺栓孔，把螺栓等效为如图7所示的分区域薄层单元。

图6 轴向刚度随拧紧力矩的变化

最终建立的机匣连接件简化模型如图8所示。采用2阶4面体单元，设定网格尺寸为10 mm。该简化模型共有14万个节点，42万个自由度，与超模型相比，连接机匣模型规模降低到原来的1/10。

根据式（23）和式（24）确定不同预紧力下的分区域薄层单元的弹性模量，见表2。

图7 薄层单元建模

图8 螺栓连接机匣简化模型

表2 薄层单元的弹性模量

图9 连接试验机匣模态试验

2.3 螺栓机匣试验测试

在连接螺栓上施加3～11N·m的拧紧力矩时，测试连接机匣的模态频率如图9所示。采用力锤激励，加速度传感器测量；采集激励信号和响应信号，通过频响分析软件对测得的频响函数进行分析，并提取连接机匣前8阶频率。

2.4 结果对比

在螺栓拧紧力矩分别为3、7、11 N·m时，分区域薄层单元模型仿真频率与机匣试验频率见表3。从表中可见，连接机匣试验频率随着拧紧力矩增大而加快，第3、4阶频率变化最为明显，说明螺栓预紧力大小对连接机匣的动力学响应有较大影响。简化模型仿真频率与机匣试验频率相比，最大误差仅为2.83%，满足工程设计要求。由此可见，分区域的薄层单元建模方法能准确地模拟在不同预紧力下螺栓连接结构的刚度变化，建立有效的连接结构有限元模型。

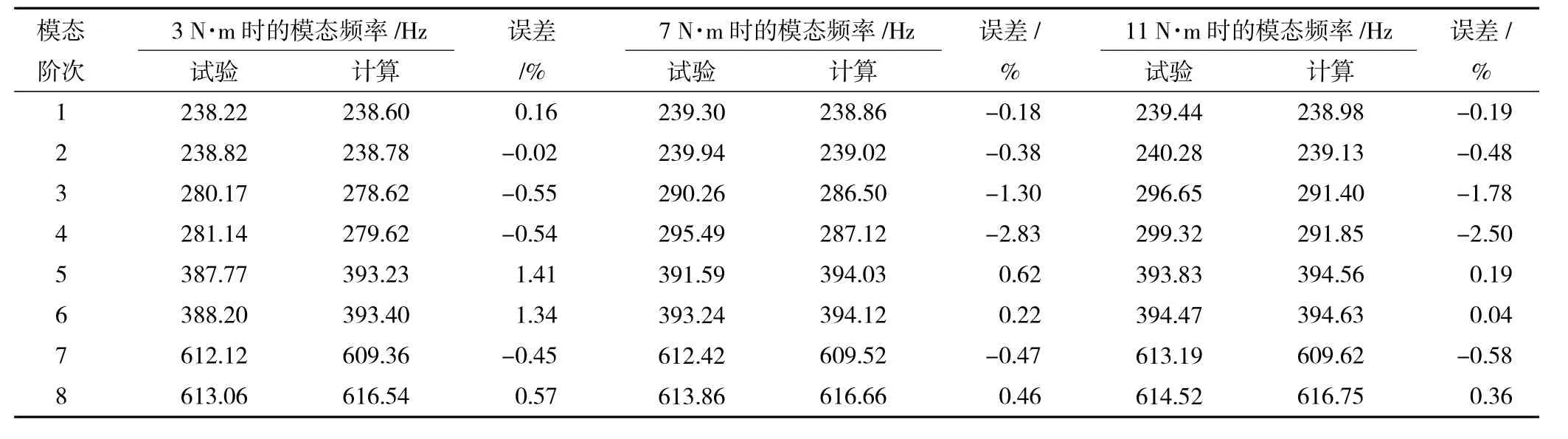
表3 在拧紧力矩为3、7、11 N·m时分区域薄层单元简化模型的模态频率

3 结论

本文基于螺栓连接超模型的刚度理论、赫兹接触理论以及M-B分形模型，考虑螺栓的数量和法兰边的接触，建立了分区域薄层单元的螺栓连接简化建模方法，推导了不同预紧力下分区域薄层单元弹性模量的计算公式。通过模态试验验证了不同螺栓预紧力简化建模方法的正确性，得到如下结论:

螺栓预紧力对机匣连接部分的法向接触刚度影响较大，随预紧力的增大，法向接触刚度增加，之后逐渐趋于平稳；连接机匣的各阶固有频率也逐步加快，之后也趋于平稳。

本文连接接触的建模，没有考虑连接接触非线性阻尼的影响，但为进一步在此方面深入探索螺栓连接动力学的问题奠定了基础。