基于DIS实验“探究影响向心力大小因素”的改进及其拓展

河北省华北油田第三中学(062552) 李富恩

河北省沧州市教育局(061001) 王晓梅

北京林业大学工学院(100083) 何彦雨

1 引言

圆周运动是高中物理动力学部分的重点和难点知识，向心力又是描述圆周运动的重要物理量之一，“向心力”一节内容还是曲线运动的重点和难点，具有承上启下，承前启后的作用。课本中对本节课的实验只是定性研究，不能得出定量结论，向心力大小也只是通过向心力演示器在转动中露出的小格数来判定向心力大小，实验误差非常大。针对这些情况，结合我校的DIS设备，对原有实验器材进行改进，最终成功利用实验探究的方法定量探究出向心力和各个因素之间的定量的关系。通过学习，既能使学生从对圆周运动的表面认识上升到理论分析，又能让学生从生活中的圆周运动分析提高到对天体运动及带电粒子在电磁场中的分析及推演。

2 实验设计与创新要点

教材从理论的角度出发，根据牛顿第二定律，推导出做圆周运动的物体受到的合外力的大小和方向，即向心力的大小和方向，根据前一节向心加速度的表达式，根据牛顿第二定律，可得：

这样的推导不利于学生掌握，更没有实验理论作为依据。为此我们对本节内容做了改进，让学生在定量实验探究的基础上建立起知识的框架，充分发挥物理实验的强大功效。本实验创新点主要是改变了向心力公式只能定性感知，而不能定量探究的现状。

(1)创新一

在原有向心力演示仪基础上，引导学生发现实验弊端，根据弊端进行改进。改进后的向心力演示仪能保证物体做匀速圆周运动，向心力的大小很稳定，不足的地方在于向心力大小读数不够准确。

(2)创新二

第二个改进让学生容易想到用弹簧测力计来测量力的具体数值。但这一实验中，小球的速度难以测量或进行定量改变，再加上运动着的弹簧测力计根本读不出准确数值。

(3)创新三

第三个改进利用手机拍照功能，记录弹簧测力计的读数，仍然难以对向心力与各个因素间的关系进行定量的探究。

(4)创新四

有了前面的分析实验，进行了第4次实验，让学生从匀速圆周运动的角度出发，利用DIS实验探究向心力大小与各个因素间的定量关系。

3 实验教学过程

3.1 实验一(初步感受，引入新课)

使用传统的向心力实验演示仪(见图1)进行演示实验，让学生感知向心力大小与质量m、线速度v和半径r有关，得到初步认识，通过教师演示学生很容易发现：

(1)控制线速度v、半径r不变：改变小球质量，实验过程中发现，小球质量越大，竖直的立杆中露出的小格数越多，即实验结果是：质量m大，F向也大。

图1 传统向心力演示仪器

(2)控制质量m、角速度ω不变：通过改变小球在槽中不同的位置，即改变了小球圆周运动的半径，实验发现，小球离圆心越远，竖直的立杆中露出的小格数也越多，即实验结果是：半径r越大，F向大。

(3)控制质量m、半径r不变：通过增大小球转动的角速度，发现竖直的立杆中露出的小格数也越多，即实验结果是：角速度ω越大，F向也越大。

但我们发现：实验过程中难以保证小球做匀速圆周运动；竖直的立杆中露出的小格数也很不稳定，难以量化。所以需要对实验进行改进，随即进行实验二。

3.2 实验二：引导学生创新思考

在前面的实验中手摇演示仪转动，实验中不能记录转动速度，也不能控制转动时小球匀速转动，怎么办?学生思考片刻想到了：用电机带动小球转动；在研究向心力跟转速关系时，需要改变转速，学生借助电风扇的原理，又想到了用可控转速电动机，完美的突破了能够改变匀速转动的转速问题。

又引发新的思考：能够使物体做匀速圆周运动；实验过程转动平稳，力的大小也应该稳定下来，进行实验数据采集时，不能通过露出来的小格数进行采集，这样的误差很大。

3.3 实验三：创新思考解决向心力大小的读数问题

通过之前的学习，学生很容易想到使用弹簧秤测量力的大小，貌似很简单就解决了。但问题再次出现：匀速转动的小球挂在弹簧秤一端，快速转动着，如何读数呢?充分利用手机的录像或拍照功能就可解决小球稳定的匀速圆周运动和弹簧秤测量力大小的读数难题。

依然存在的问题：实验装置难以固定和改造，手机拍照读数存在很大的误差。为此引出了这个实验的核心部件：DIS数字实验系统，于是进行以下实验。

3.4 实验四：利用DIS实验定量探究向心力大小与各物理量间的关系

实验仪器：朗威光电门传感器、力传感器、向心力实验器，实验装置如图2所示。装置安装好，拨动旋臂使之做圆周运动，转动几次，系统记录下了小球运动过程中相应量的数据。

图2 向心力大小DIS探究演示装置

(1)控制m、r不变，探究向心力Fn与转动角速度ω的关系。

实验时将小球放置在悬臂槽中一固定位置，即控制好小球的运动半径。将此时小球的运动半径和小球的质量输入窗口到下面的表格中，拨动悬臂使之做圆周运动，坐标系内将自动显示一组F－ω数据点，如图3所示，点击“一次拟合”“二次拟合”，得出2条拟合图线。观察可见，一次拟合的直线与数据点偏差太大，说明F与ω之间并不是一次函数关系；二次拟合得到的曲线，与数据点契合度极高。说明m、r不变的情况下，向心力F向与角速度ω的关系很像二次函数关系。随机进行第二步操作。

图3 向心力大小与角速度的关系

点击F－ω2图像，对数据点进行“一次拟合”，即得到如图4所示的图线，通过观察在误差允许范围内接近过原点的直线，得到结论：在m、r一定的情况下，向心力的大小与ω2成正比。

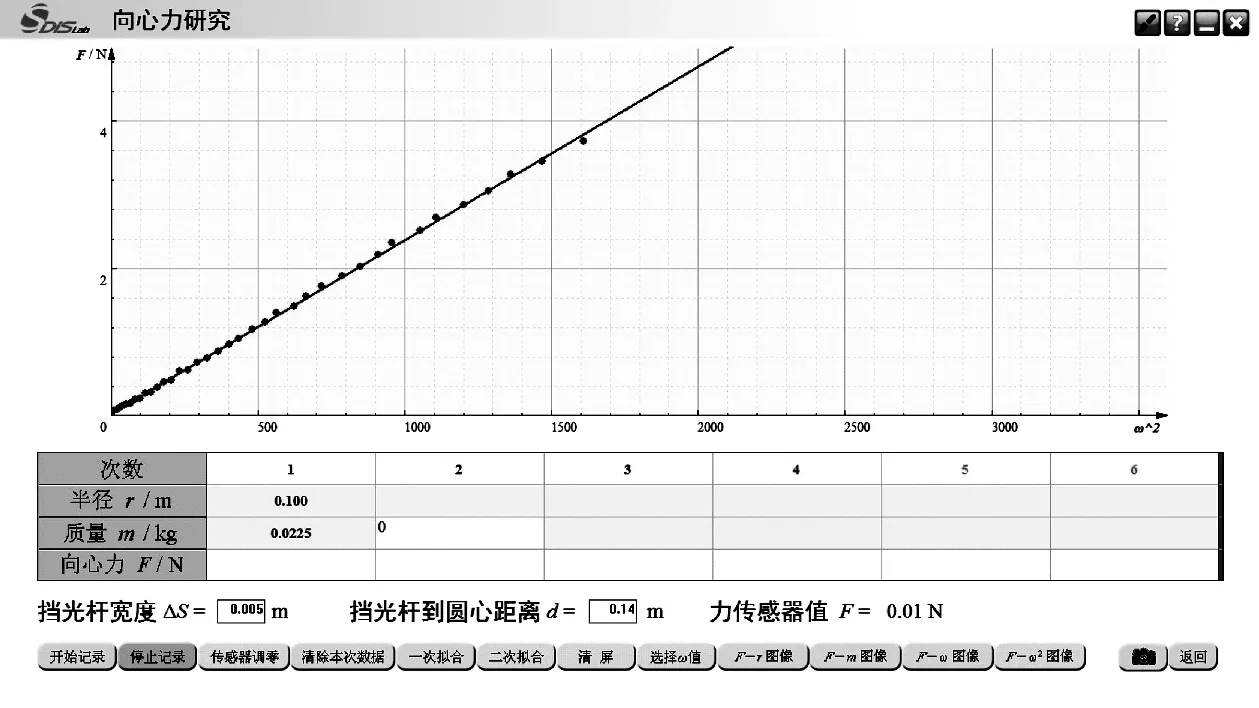
图4 向心力大小与角速度平方的关系

(2)控制m、ω不变，探究向心力Fn与半径r的关系。

改变小球运动的半径，重复实验，得出几组F－ω数据点，点击选择“选择F值”，用鼠标选取相同角速度时不同半径对应的F值，如图5所示，系统自动记录在窗口的表格中。点击F－r图像，同样得到一条直线，在误差范围之内可以认为是一条过原点的直线。得出结论：在m、ω一定的情况下，向心力Fn的大小与圆周运动半径r成正比。

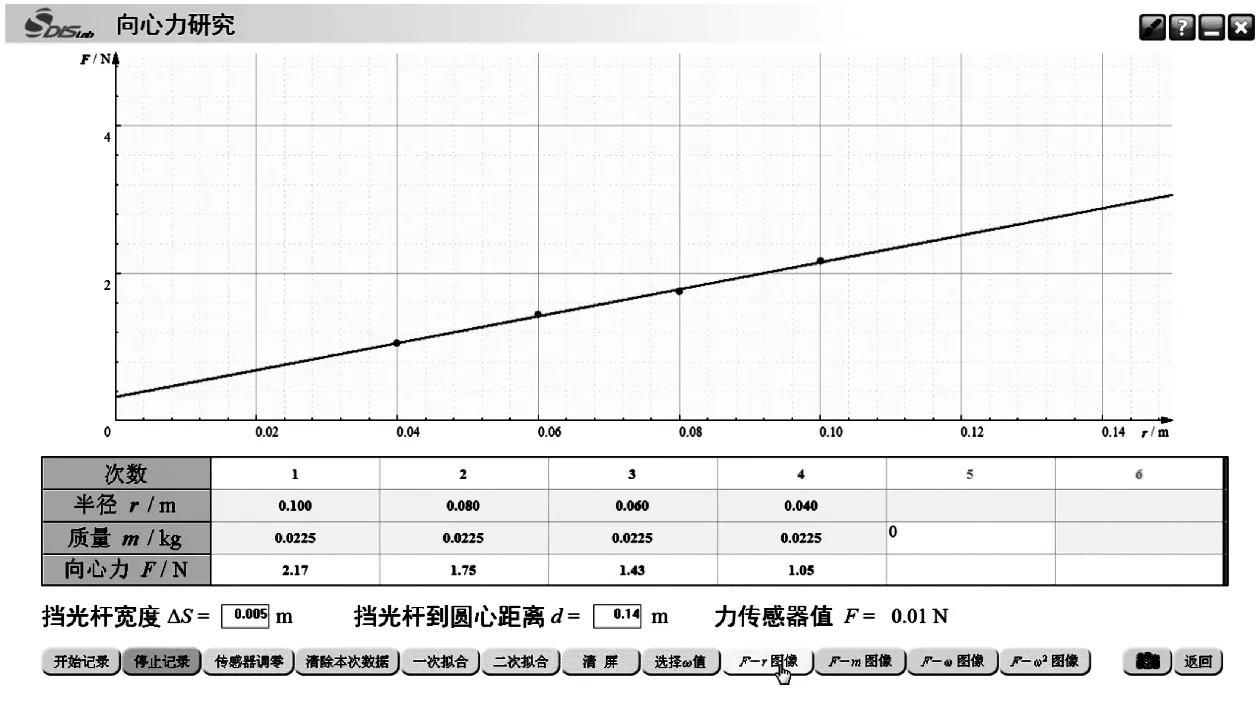
图5 向心力大小与半径的关系

(3)控制r、ω一定：探究向心力Fn与小球质量m的关系。

保持小球的运动半径不变，改变其质量，重复前面的实验，同样得出几组F－ω数据点，点击选择“选择F值”，用鼠标选取相同角速度时对应不同质量的F值。点出“F－m图像”得到如图6所示的拟合图线，同样认为在误差允许范围内，近似认为是一条过原点的直线。得到结论：在r、ω一定的情况下，向心力Fn大小与小球质量m成正比。

进行完以上3个实验，可以得到小球匀速圆周运动向心力的公式：Fn＝m ω2r。

(4)控制m、r不变，探究向心力Fn与线速度v的关系。

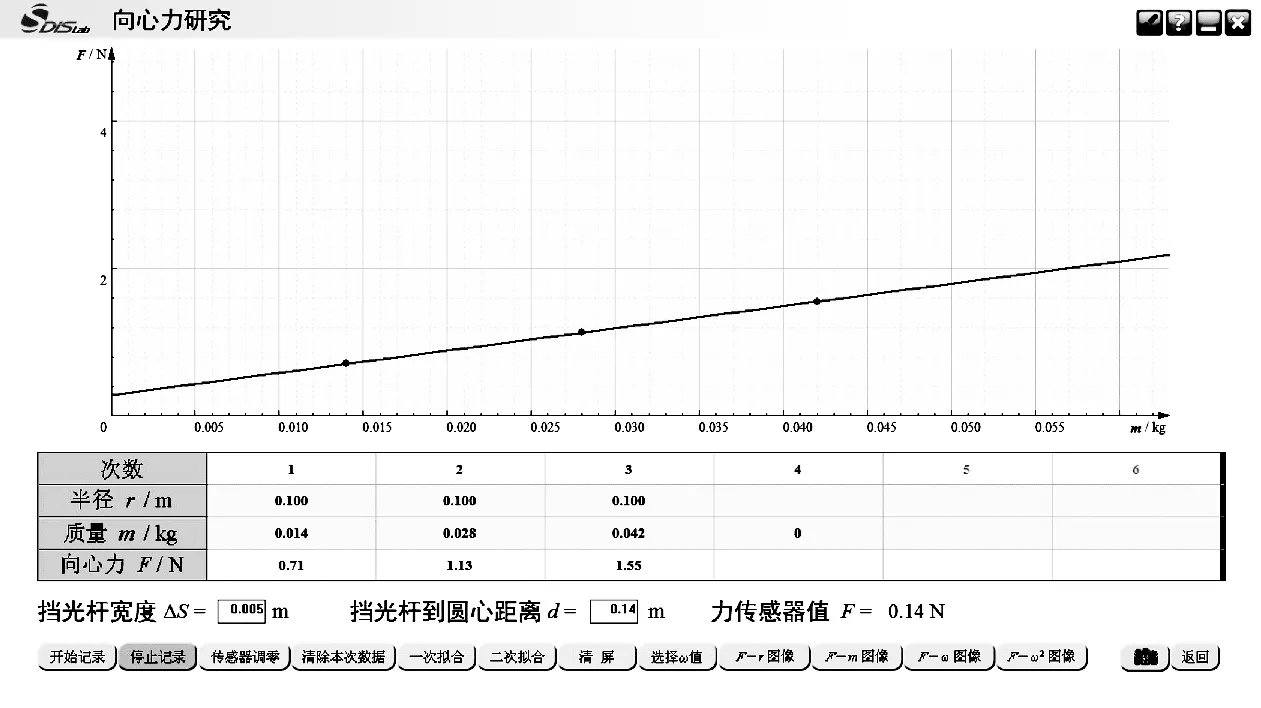
图6 向心力大小与小球质量的关系

利用前面小球向心力F和ω的几组数据点，如图7所示，让学生选择一种颜色的数据点，用鼠标选择几种不同的ω，系统会自动记录下对应的向心力F数值，并显示在表格中。根据已知的半径，由υ＝ω r分别算出各自的线速度υ，当υ的比值υ1∶υ2∶υ3＝1∶2∶3时，看向心力F的比值是不是非常接近F1∶F2∶F3＝1∶4∶9。如果此结果成立，就说明在m、r一定时，向心力大小与速度的平方成正比。

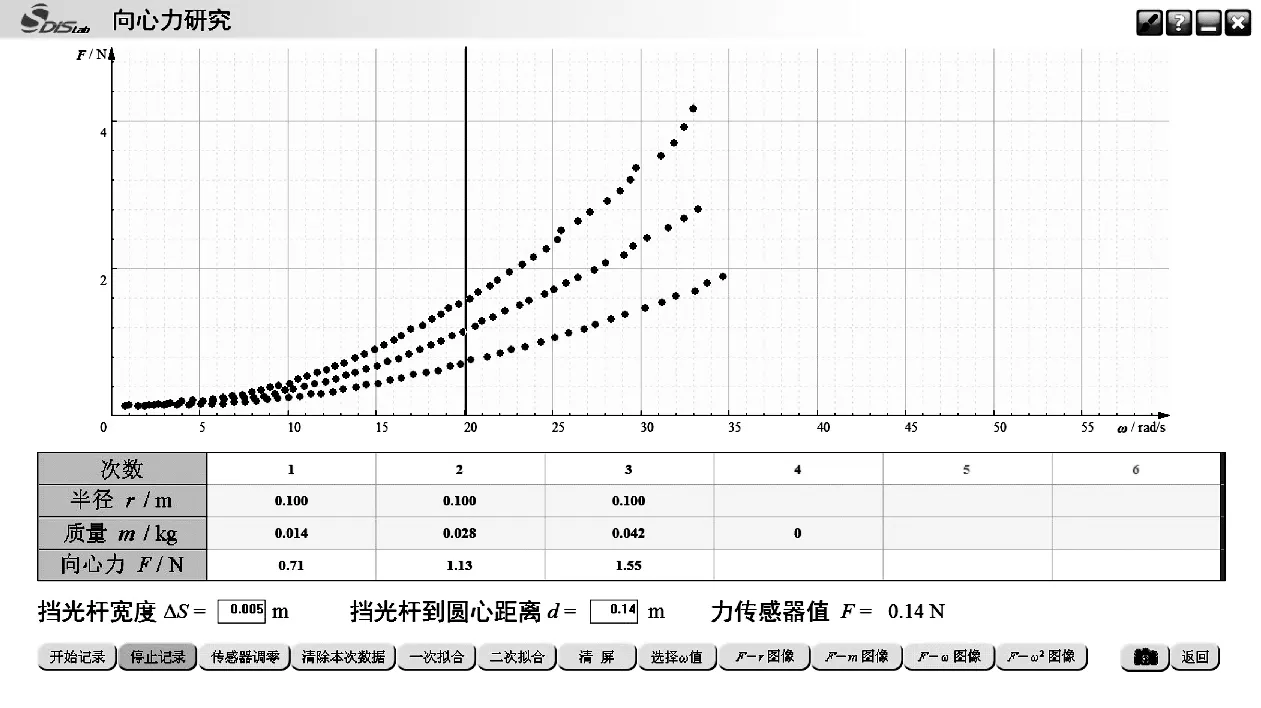
图7 向心力大小与角速度的关系

4 实验效果评价与反思

本节课教学设计有以下几个亮点：

(1)突破教材内容，改变了向心力公式只能定性感知，不能定量探究的现状。

(2)从物理方法分析，本节课的设计很好地体现了控制变量法的使用，培养了学生严谨、科学的实验态度和能力。

(3)使用传感器进行探究实验提升实验效率，实验效果非常明显。通过这些创新和改进，提高了课堂效率，取得了很好的教学效果。充分发挥数字实验的功效，激发学生进行科学探究的创新精神。