基于数学实验的初中数学课例分析
上海师范大学数理学院(200234) 张庆庆
华东师范大学教师教育学院(200062) 姜浩哲
1 引言
北京师范大学曹一鸣教授认为“数学实验是指为了获取某种数学理论、检验某个数学猜想、解决某类问题,实验者运用一定的物质手段,在数学思维活动的参与下,在特定的实验环境下进行的探索及研究活动。”所谓“纸上得来终觉浅,绝知此事要躬行”,在数学课程中创设数学实验,目的是通过实验,向学生展示数学知识的探究过程,让学生能够在数学实验中,发现数学的美、理解数学的本质、感受数学的睿智,最终学会运用数学,以此既能让学生学得数学相关的知识,又能培养探索能力,形成学生的批判性思维。
在初中数学教学过程中,数学实验主要是学生运用相关教具,结合思维活动,通过自己的动手以及思考,形成对数学的认知,培养学生核心素养的活动。孙朝仁学者认为“数学实验作为积累‘基本活动经验’的重要载体,在日常的数学教学中发挥着不可替代的作用”。
2 数学实验的类型
基于已有的数学实验分类方式,结合2015—2018年发表的10个具有代表性的初中数学实验课例分析,从实验目的来看,数学实验可以分为理解型、验证型和探索型;从实验工具来看,数学实验可以分为实物实验和计算机实验。本文将从实验目的出发,结合实验工具,对10个数学实验课例进行具体考察。
2.1 理解型数学实验
课例“认识无理数”是以实物十面骰子以及计算机Excel为工具,让学生理解无理数为目的的数学实验。教师先让学生合作掷十面骰子的实验,将第一个掷出的点数作为整数位,其后掷出的点数依次作为小数位,并引导学生思考:得到的不断延伸的小数有什么特点?是否为无理数?然后利用Excel估算面积为2的正方形的边长,培养学生的数感,学生因此能更加自然地理解无理数的基本特征。
课例“平移翻折旋转”是以实物透明纸和网格纸为工具,以让学生理解三种变换方式为目的的数学实验。教师通过让学生在透明纸和网格纸上将原始图像进行一系列变换之后得到目标图像的实验,培养学生的空间观念,让学生更好地理解平移、翻折和旋转三种变换方式的基本特征。
课例“平行线的性质和判定”是以实物折纸为工具,以让学生理解平行线的性质及判定为目的的数学实验。教师用长方形纸条折平行线引入,学生在动手实验的过程中运用平行线的判定定理来证明自己所折的是平行线;然后一步步深入,如图1所示,教师给出任意线段EF,引导学生过点P折出EF的垂线,再过点Q折出这条垂线的平行线。学生利用平角的角平分线的性质,过点P折叠,使得点E落在线段EF上,所得折痕就是线段EF的垂线;同样的道理得到过点Q的垂线,利用同位角相等判定平行线。通过折纸实验,培养学生空间观念,帮助学生回顾和深刻理解平行线的性质和判定。
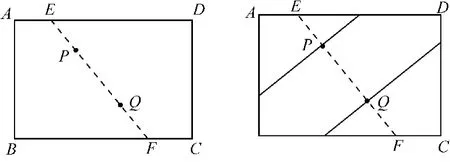
图1 过一点折已知线段的垂线
2.2 验证型数学实验


图2 由四个全等直角三角形拼出的边长为c或者(a+b)的正方形
课例“在数轴上表示无理数”是以实物圆形纸片以及计算机软件几何画板为工具,以验证无理数可以在数轴上表示为目的的数学实验。教师先请学生将一个周长为π的圆形纸片贴在数轴上滚动一周以求得π在数轴上的位置,但是滚动过程中存在一些误差,经过大家的讨论改进,学生将绳子绕圆形纸片一周,然后将这段长度在数轴上量出来,初步把无理数π在数轴上表示了出来;此时实物验证的方法会有误差,学生在教师指导下借助计算机验证,在几何画板上将圆形的滚动轨迹表示在数轴上,精确得到π的位置。通过实物和计算机实验,培养了学生的数感和几何直观能力,学生能发现在数轴上表示无理数的方法。
2.3 探索型数学实验
课例“反比例函数”是以实物天平为工具,以重构反比例函数历史过程为目的的数学实验。教师使用了如图3所示的天平模型,点O是支点,左右两边A、B处悬挂重物,为方便理解,将OA的距离设为acm,OB的距离设为bcm。A处悬挂的重物质量为mg,B处重物质量为ng。学生在教师的指导下探究:当a、n不变时,b和m之间的关系。做完这组实验后,教师再启发学生思考和探究:当a、m不变时,b和n之间的关系是怎样的,从而引出反比例函数。通过天平实验,培养了学生的模型思想,学生更易接受反比例函数的概念。
课例“三角形的边”是以实物牙签和直尺为工具,以探究三角形三边不等关系为目的的数学实验。教师引导学生将不同长度的牙签摆成三角形,然后改变三角形两边的长度,并让学生探究第三边长度的取值范围。学生发现牙签的长度存在误差,既而调整为直尺继续探究。通过数学实验,培养了学生的空间观念,学生更加了解了三角形三边的不等关系。

图3 天平模型
课例“多边形外角和”是以实物拼图和计算机软件几何画板为工具,以探究多边形外角和为目的的数学实验。教师先用三角形、四边形和五边形让学生进行讨论和探究,学生借助拼图,将多边形外角和拼在一起,发现合成了一个圆周。为了规避实物实验带来的误差,学生在教师指导下又用几何画板进行验证,将所有的外角汇聚到一点,得到的也是一个圆周(见图4),由此得到多边形外角和与边数无关,始终为360°。通过数学实验,培养了学生的空间观念和探究精神。
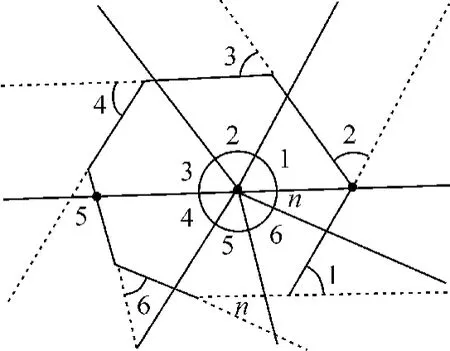
图4 几何画板求多边形外角和
课例“三角形中位线定理”是以实物折纸为工具,以探究三角形中位线为目的的数学实验。教师先以直角三角形(见图5)引入,让学生将点A与点C重合,观察折痕的特性;然后将点B与点C重合,观察讨论折痕的特性;教师在此基础上引入三角形中位线的定义,而后引导学生折出一般三角形的中位线(见图6),探究中位线与第三边的关系。通过折纸实验,培养学生的空间观念。
课例“二次函数图像与性质”是以计算机软件几何画板为工具,以探究二次函数图像与性质为目的的数学实验。学生先讨论二次函数y=ax2(a≠0)中a对函数图像变化的影响,然后利用几何画板,调整a的取值,来具体观察二次函数图像的变化规律,做成实验表格进行交流。对于y=ax2+k(a≠0)、y=a(x-h)2+k(a≠0)等不同的形式中的参数对图像变化的影响也做同样的探究。通过数学实验,培养了学生的空间观念。
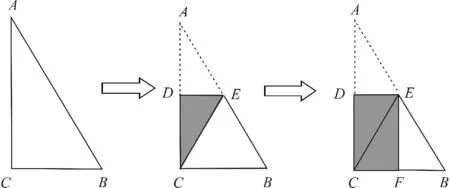
图5 直角三角形的中位线

图6 一般三角形的中位线
3 数学实验的特点
根据数学实验的目的、工具等因素,数学实验表现出如下特征。
(1)工具性,即使用工具,包括纸张、模型、作图工具、计算机等进行实验;
(2)操作性,即实验必须通过学生动手操作去完成;
(3)情境性,即实验的设计与实施必然置于某种情境之中;
(4)探究性,即整个教学过程是一个学生对知识的探究过程。
基于上述特征,我们依次对初中阶段数学实验课例进行分析。
“认识无理数”是人教版八年级上册的内容,教科书通过面积为25d m的正方形画布求边长引入算术平方根的概念,继而引出无限不循环小数。数学实验课例中,教师通过让学生合作掷十面骰子,将第一个掷出的点数作为整数位,其后掷出的点数依次写在小数位,让学生思考得到的不断延伸的小数有什么特点,体现了工具性、操作性、情境性。学生通过Excel探究面积为2的正方形的边长,体现了探究性。
“平移 翻折旋转”是人教版初中3年都涉及的知识点,“平移”在7年级下册,教科书通过几组在同一直线上的相同的图形来探究经过怎样的变换得到的;“翻折”在8年级上册,教科书通过轴对称图形引入;“旋转”在9年级上册,通过钟表和风扇的旋转引入。数学实验课例中,教师通过让学生用透明纸和网格纸临摹图形,找出变换规律,体现了工具性、操作性、情境性。学生自己通过操作实验,得到图形的变换过程,体现了探究性。
“平行线的性质和判定”是人教版7年级下册的内容,教科书通过用直尺和三角板画平行线的方法得到“同位角相等,两直线平行”。数学实验课例中,教师通过让学生过线段上的一点折该线段的垂线,以及过线段上的另一点折出平行于这条垂线的线段,并且让学生自己证明为什么平行,体现了工具性、操作性、情境性以及探究性。
“勾股定理的证明”是人教版9年级下册的内容,教科书给出毕达哥拉斯证明法的提示。数学实验课例中,教师引导学生用拼图的方式将4个全等直角三角形拼成边长为a+b或者c,学生通过等面积法验证勾股定理,体现了工具性、操作性、情境性。学生探究拼图的过程体现了探究性。
“在数轴上表示无理数”是人教版8年级下册的内容,教科书上是在利用勾股定理将无理数在数轴上表示出来的。数学实验课例中,学生通过在数轴上滚动圆以及用绳子度量圆的周长的方式将无理数在数轴上表示出来,并且通过几何画板更加精确地验证这一课题,体现了工具性、操作性、情境性。学生发现实物实验的误差,然后利用计算机实验的过程体现了探究性。
“反比例函数”是人教版9年级下册的内容,教科书通过已知路程,平均速度v随全程运行时间t的变化而变化这一问题引入反比例函数的概念。数学实验课例中,教师通过天平模型,控制一端的重量和到支点的距离,探索另一端重物的重量和到支点的距离之间存在的关系,引入反比例函数,体现了工具性、情境性和探究性。因为是教师演示,所以在操作性上略显不足。
“三角形的边”是人教版8年级上册的内容,教科书对三角形的定义为“不在同一直线上的三条线段首尾依次相接所组成的图形”,由此引出对三角形三边不等关系的探究。数学实验课例中,教师让学生自行利用不同长度的牙签进行实验,探索已知两条线段的长度,第三条线段长度的取值范围,体现了工具性、操作性、情境性。学生在探究过程中发现牙签长度的误差,调整为用直尺作为实验工具,体现了探究性。
“多边形的外角和”是人教版8年级上册的内容,教科书通过六边形任何一个外角加上与它相邻的内角等于180°,利用多边形内角和求得六边形外角和为360°,然后拓展成一般的多边形。数学实验课例中,教师引导学生利用拼图以及几何画板平移外角,验证得到多边形外角和始终为360°,体现了工具性、操作性、情境性和探究性。
“三角形中位线定理”是人教版8年级下册的内容,教科书是通过构造平行四边形证明得到三角形中位线平行第三条边且等于第三条线的一半。数学实验课例中,教师引导学生通过折纸,折出三角形中位线,能够直观感受到三角形中位线与第三条线的关系,体现了工具性、操作性、情境性.学生通过数学证明三角形中位线定理的过程体现了探究性。
“二次函数图像与性质”是人教版9年级上册的内容,教科书通过描点法画出二次函数图像。在数学实验课例中,教师先让学生进行讨论,然后学生借助几何画板通过调整不同系数,观察系数对于二次函数图像的影响,体现了工具性、操作性和探究性,但是在情境性方面略有不足。
初中阶段数学实验课例的对比分析见表1。

表1 初中阶段数学实验课例的特点
表1对初中阶段各课例中数学实验的特点进行了汇总,大部分的数学实验课例具有工具性、操作性、情境性和探究性。南京师范大学谭顶良教授认为 “初中数学实验课堂教学评价的目的旨在改进教师教与学生学的行为”,因此在进行数学实验教学中应更关注操作性与探究性,使学生积极参与到探索真理的过程中去,尊重学生在数学实验中的主体地位。

