基于量纲分析的油炒表面换热系数预测模型
张宏文何腊平,2邓 力,2李翠芹冯伦元陈翠翠余冰妍常 瑞
(1. 贵州大学酿酒与食品工程学院,贵州 贵阳 550025;2. 贵州省农畜产品贮藏与加工重点实验室, 贵州 贵阳 550025;3. 贵州大学化学与化工学院,贵州 贵阳 550025)
中式烹饪历史悠久,技法形式复杂多样,其中油炒具有过程短促激烈、非稳态性显著等特点,复杂性远高于水传热和汽传热[1],是中式烹饪独有的典型技法。油炒烹饪的过程特征是开放容器中被搅拌流体—颗粒食品的加热过程。在该过程中传热方向是热源→容器→流体→食品颗粒[2]。流体—颗粒表面换热系数(fluid-to-particle heat transfer coefficients,hfp)是描述传热的关键性过程参数。hfp是流体与单位面积的食品颗粒表面之间存在温度梯度时,流体对流到颗粒表面的热对流速率,其数值取决于油炒过程中流体与食品颗粒相对运动速度、流体热物性及食品颗粒特征的综合。hfp对油炒烹饪中食品颗粒的全局温度分布有决定性影响,从而影响中心成熟值(Mc值)、表面过热值(Os值)等[3]温度依赖性品质动力学参数,在烹饪品质控制与优化中有重要意义。目前,中国的烹饪行业产值已达到4.27万亿元[4],随着食品加工业的快速发展,对烹饪的基础研究日益迫切,亟需油炒等烹饪过程中诸因素下hfp的准确测量及预测。
在食品热处理中hfp的获得难度较大,主要有集中参数法、表面热流量测量法和中心温度测量法[5]。文献[6]中总结实测食品颗粒温度及hfp的具体方法有:静态颗粒法[5,7-8]、移动热电偶法、液晶法、发射法、微生物法[时间温度积分器(time-temperature integrators,TTIs)[9-10]]。由于油炒烹饪过程中食品颗粒快速无规则移动,静态颗粒法、移动热电偶法等试验测定手段存在较大误差,液晶法和发射法准确性也不高,微生物法则存在制作繁琐问题。因此,采用数值法并结合传热学试验是计算得到较为准确的hfp唯一方法。
量纲分析是Backingham于20世纪初提出的一种在物理领域中建立数学模型的方法,可有效分析和探索物理量之间的关系[11]1-8。相较于其他计算方法,该方法对数据进行合理降维,在减少计算量的同时保证计算精度,能最大程度地反映影响建模的关键参数。早在1938年,Froszling利用量纲分析法建立了空气中废水的hfp:Nu=2.0+0.55Re1/2Pr1/3。在食品热处理领域,Chandarana等[12]得出立方体硅脂颗粒分别在淀粉液和水中hfp的无量纲预测式:Nu=2.0+0.028 2Re1.6Pr0.89和Nu=2.0+0.033 3Re1.08。Zuritz等[13]研究了蘑菇形铝质颗粒在CMC溶液中的传热过程,得到了无量纲预测式:Nu=2.0+28.37Re0.233Pr0.143(dm/dt)1.787。目前利用量纲分析方法预测hfp主要在杀菌领域[14-15],而应用于油炒过程中hfp预测尚未报道。
本研究基于量纲分析法中Π定理推导hfp的无量纲预测模型,考察油炒过程中不同火候、不同流体流速模拟食物搅拌与颠锅过程,结合实测hfp验证模型准确性。以期为油炒烹饪提供一种普遍适用、方便、经济的hfp研究测定方法。
1 材料与方法
1.1 试验材料
猪里脊肉、食用调和棕榈油:市售。
1.2 仪器与设备
计算机:E5-572G-528R型,8 GB内存,I5-421M双核处理器,宏碁电脑(上海)有限公司;
烹饪传热学及动力学数据采集分析系统:贵州大学自研[16];
铠装热电偶:WRTK-103型,宁波奥崎自动化仪表设备有限公司;
可调速恒温油浴锅:DF-101T-5型,上海力辰邦西仪器科技有限公司;
切片机:BL658型,深圳市博莱电子电器有限公司;
S型皮托管:SPT-08-500型,上海亿欧仪表设备有限公司。
1.3 烹饪流体—颗粒多孔介质热/质传递模型
1.3.1 控制方程 在油炒过程中,食品颗粒内部任一位置的温度随时间的变化而变化,在笛卡尔坐标系中,呈现三维非稳态温度分布;颗粒无内热源,热物理参数密度、比热容、导热系数相对温度,可视为常数,因此,内部导热过程适用简化的三维非稳态导热微分方程[2]:

(1)
式中:
ρp——食品颗粒密度,kg/m3;
Cpp——食品颗粒比热容,J/(kg·℃);
T——食品颗粒微元温度,℃;
t——时间,s;
kp——食品颗粒导热系数,W/(m·℃);
Δ——拉普拉斯算符。
1.3.2 初始条件和边界条件
(1) 初始条件:初始温度Ts为室温24 ℃,Tf为流体温度,由油浴锅控制。
(2) 边界条件:流体—颗粒对流加热过程中,其边界控制方程为:
kp▽T=-hfpTs-Tf,
(2)
式中:
▽——汉密尔顿算符;
hfp——流体—颗粒表面换热系数,W/(m2·℃);
Ts——颗粒表面温度,℃;
Tf——流体温度,℃。
目前数值法计算hfp的研究尚不充分,本课题组前期建立了考虑表面蒸发的烹饪流体—颗粒多孔介质热/质传递模型[17],经解析法验证,实测与模拟的时间—温度的相关系数R达到0.997以上。根据数学物理方程解的唯一性定律[18],当非稳态传热的定解条件一定时模型的解唯一,采用试差法计算实测与模拟的时间—温度相关系数的最大值是,此时模型中的hfp认为是实际值。
1.4 量纲分析的基本原理:Π定理
Π定理[11]9-18[19-20]是量纲分析理论的核心,由美国物理学家Buckingham于1914年提出,用数学公式解释Π定理如下:
设n个物理量之间满足下列函数关系式:
f(x1、x2、……、xn)=0,
(3)
式中:
x1、x2、……、xn——物理量。
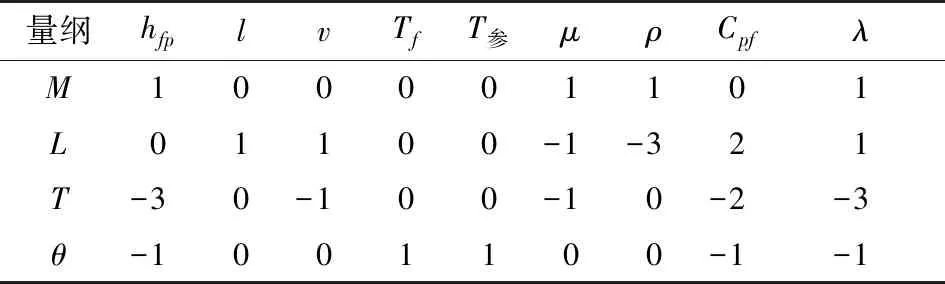
n个物理量中含有p个基本量纲(p F(Π1、Π2、……、Πm)=0, (4) 式中: F——待求函数关系; Π1、Π2、……、Πm——无量纲数群(准数),且m=n-p。 综上,说明Π定理将多因素影响的物理系统中的各变量经过交叉计算,导出较少无量纲准数,有利于抓住影响系统的关键因素,从而构建物理方程式的结构形式。 1.5.1 影响烹饪过程中hfp的主要因素 根据传热学原理[21]可知,影响表面换热系数的因素有食品颗粒的特征尺寸、温度、流体的流速、黏度、密度、比热容以及导热系数等。其中,温度是主导因素[5,22-23],为了温度的无量纲化,将温度分为流体温度Tf和参考温度T参。用函数关系式表达为: f(hfp,l,v,Tf,T参,μ,ρ,Cpf,λ)=0。 (5) 式(5)中9个物理量的符号、单位及量纲见表1,可以看出其由4个基本量纲:长度L、质量M、时间T和温度θ组成。 表1 试验物理量及量纲 1.5.2 确定无量纲Π数的数目 依据Π定理,无量纲Π数的数目: m=n-p=9-4=5。 (6) 若Π1、Π2、Π3、Π4和Π5表示无量纲准数,则式(5)可表示为 Π5=F(Π1,Π2,Π3,Π4)。 (7) 1.5.3 确定准数形式 以长度L、质量M、时间T和温度θ作为基本量纲,建立其量纲矩阵,见表2。 通过MATLAB软件中null函数对表2中量纲矩阵进行齐次线性方程求解,得到式(8)中5个无量纲准数: 表2 量纲矩阵 (8) 将式(8)中各Π项进行代数变换,得到式(9)中的4个无量纲准数: (9) 为了简便,假设T参为100 ℃,同时,该试验的9个变量中,除hfp为因变量外,其他均为自变量,所以将含有hfp的Π4可作为因变Π项,应满足: (10) 此时,方程等号两边的量纲必须相同,当用基本量纲的幂次式表示时,各个基本量纲的幂次相等,称为量纲齐次性。式(10)以幂函数的形式表示为: (11) 即, Nu=ReaPrb(Tf/100)c。 (12) 1.6.1 原料准备 将购买的新鲜猪里脊肉切分后放入冰箱-18 ℃冷冻室,12 h后用切片机切割。为保证后续热电偶准确插入肉片中心,采用半厚粘接法[24],即先将肉片切割为试验所需厚度的1/2,后用微量的透明耐热结冷胶粘连,粘连好的肉片可以耐受高温加热,不会出现起泡、分离等影响数据采集的现象。将肉切为4 cm×4 cm(长×宽),厚度为0.1,0.2,0.3,0.4 cm的规格,再用结冷胶粘连,使之最终形成厚度为0.2,0.4,0.6,0.8 cm的肉片,置于冰箱4 ℃冷藏室12 h左右。 1.6.2 试验过程 首先使用标准温度计校准油浴锅油温和热电偶温度。将肉片从冰箱中取出置于室温下,待肉片温度接近室温时,开启烹饪传热学及动力学数据采集系统,连接电脑,用采集系统中热电偶末端插入肉片的几何中心处,如图1所示。按照表3所示的试验条件,在可调速恒温油浴锅中进行油炸试验,每组试验5次,同时用采集系统记录中心—时间—温度。 图1 试验装置及半厚粘接法示意图 1.6.3hfp的试算法计算 假设一个hfp,由1.3烹饪流体—颗粒多孔介质热/质传递模型中得到模拟中心—时间—温度,将1.6.2中得到实测中心—时间—温度平均处理。在MATLAB中计算实测与模拟的中心—时间—温度的拟合优度:相关系数R;改变hfp,先以50 W/(m2·℃)为精度,后以10 W/(m2·℃)为精度,重复性地计算拟合优度,选择拟合优度最好的hfp,作为本次试验的hfp。 表3 试验条件† 1.6.4 流体的热物性参数 可调速恒温油浴锅中为食用级棕榈油,热物性参数如表4所示。 表4 棕榈油的热物性 对式(12)的等号两端进行取对数运算:lgNu=algRe+blgPr+clg(Tf/100)+d,转化为多元线性问题,使用SPSS 23软件进行多元线性回归,记录回归模型中的系数及决定系数R2,将线性回归结果作指数逆变换之后得到各待定参数的回归值,即为无量纲预测模型。 首先验证所选择烹饪流体—颗粒多孔介质热/质传递模型和数值计算的准确性,限于篇幅,本文列举了具有代表性的100~160 ℃流体下的温度数据,即表3中试验序号2~5组,分别将猪里脊肉的数值模拟与试验测量中心—时间—温度进行对比,如图2所示。通过MATLAB中相关系数程序对模拟和实测中心—时间—温度曲线进行相关性分析,结果显示,模拟和实测两者的相关系数R>0.98,拟合性较高。因此,说明该数值模型具有较高的可靠性和准确性。 将不同试验条件下实测的时间—温度数据经1.6.3节计算得到的hfp列于下表5,hfp的范围在250~850 W/(m2·℃)。从表5可以发现hfp随温度的升高而增大,这是由于流体温度越高,食品颗粒单位面积表面的温度梯度越大,从而换热越快,与文献[7, 23, 25]的研究成果相一致。流体—颗粒相对运动速度的大小会影响hfp,流速越大,换热越剧烈,hfp越大。文献[26]量化了搅拌频率和搅拌速度对对流换热的影响,与本文的试验结果类似。文献[27]中颗粒的特征尺寸有等体积当量直径、体积/表面积和直径等,本文采用常见的等体积当量直径。本节试验表明,特征尺寸与hfp具有负相关。Ramaswamy等[28]综述了不同作者测量hfp的文献,关于特征尺寸与hfp的变化趋势少数研究者与上述不同,但从流体力学及传热学角度分析支持本节观点。 将本试验中得到的各无量纲量进行对数运算,如表6所示,转化为多元线性问题后使用SPSS 23软件进行多元线性回归分析,可得到残差散点图如图3,以及hfp与各因素的回归方程: lgNu=0.921lgRe+2.678lgPr+3.427lg(Tf/100)-3.046 R2=0.898。 (13) 从图3回归分析的残差散点分布图中可以看出,各个残差的置信区间均包含零点,但第6和13这2个数据的残差离零点较远,回归模型对原始数据的拟合效果一般,为提高式(13)中多元回归方程的拟合效果,将这2个数据视为异常点并剔除,并对剩余各点进行多元线性回归拟合分析,从而得到新的多元线性回归方程: 图2 不同温度下实测温度与模拟温度对比及相关系数R 试验序号hfp/(W·m-2·℃-1)hfp拟合相关系数R试验序号hfp/(W·m-2·℃-1)hfp拟合相关系数R13600.984 485500.998 423900.994 295000.999 534500.998 8102500.983 945900.993 9113000.983 756500.985 3124000.991 367000.985 8135900.993 975900.993 9148500.993 3 表6 各无量纲Π数 图3 回归分析的残差分布图 lgNu=0.876lgRe+3.206lgPr+4.18lg(Tf/100)-4.09, (14) R2=0.973。 修正后的多元线性回归方程的决定系数R2接近于1,说明与原回归方程相比修正后回归方程的拟合优度得到较大提高,回归方程较好地符合原始数据。将式(14)经指数逆变换之后得到各待定参数的回归值,即得到无量纲预测关系式: Nu=10-4.09Re0.876Pr3.206(Tf/100)4.18, (15) R2=0.973。 图4 Nu的实测计算值与预测模型预测值的比较 为检验上述建立油炒烹饪过程中hfp的预测模型(即无量纲预测关系式)的准确性和合理性,采用外加试验验证预测模型。为保证验证实验样本具有代表性,选取表3试验外的5组自变量的值,通过式(15)求出Nu与对应的hfp,相关参数具体见表7。 通过表7中预测模型计算值和实测结合数值计算值的hfp可知,两者的相对误差分别为0.48%,3.86%,4.67%,1.61%,3.33%。两者的平均相对误差为2.79%,满足食品与烹饪工程计算的要求,说明预测模型的误差在可接受范围内,验证了该预测模型及方法的科学性和先进性。 表7 hfp预测模型计算值与实测数据计算值的比较 经过2.3节对hfp的预测模型的准确性验证,说明该预测模型可用于实际应用,在未来的自动化烹饪中,通过传感器采集,可以实时计算出烹饪过程中的hfp,以便操作者对火候进行调控。为中式烹饪基础研究带来一种普适性的研究方法,使烹饪的基础研究更加方便、经济,对中式烹饪自动化、工程化和现代化有着深远的意义。 文献[3]提出成熟值理论,在文献[29]的完善下,最终成熟值定义为:由特定人群感官评价判定某一特定品质的成熟程度相对参考温度的等效加热时间。通常测定成熟值需要热电偶插入食品颗粒冷点,但在剧烈的油炒烹饪中并不适用,虽然TTIs法可以解决这一问题,但其不具有普适性。本文构建的预测模型可以较为准确地预测hfp,结合本文中采用的烹饪流体—颗粒多孔介质热/质传递模型,可以计算全局温度分布和中心成熟值(Mc值)及表面过热值(Os值)等参数,对食物的成熟程度进行预测,从而预判对烹饪的终止,达到科学烹饪的目的。在文献[30]中论述了基于TTIs将手工烹饪转变为自动烹饪的方法,同样,本文建立的预测方法结合TTIs为手工烹饪转变为自动烹饪提供了技术支撑,提高了准确性。 为研究油炒烹饪过程中对食品颗粒温度分布以及动力学参数有重要影响的表面换热系数hfp。基于流体—颗粒多孔介质热/质传递模型结合传热学试验模拟油炒加热过程并计算获得hfp;考察特征尺寸、温度、流速、流体性质 (黏度、密度、比热容和导热系数) 等变量因素,采用量纲分析方法对hfp涉及的主要因素进行降维处理得到Nu、Re、Pr、Tf/100 4个无量纲准数,从而得到初步预测模型:Nu=10-3.046Re0.921Pr2.678(Tf/100)3.427,R2=0.898,经过残差分析修正后获得可准确计算hfp的多元线性预测模型:Nu=10-4.09Re0.876Pr3.206(Tf/100)4.18,R2=0.973。验证实验结果表明在油炒温度为80~160 ℃ 时,相对误差最小为0.48%,最大为4.67%,该模型预测值与实测计算值拟合效果良好。但烹饪过程涉及诸多复杂因素,食品颗粒在油炒等其他烹饪过程中的品质变化复杂多变,应结合传质系数、食品颗粒导热系数等热物性参数综合考虑,虽不同的烹饪体系对传热参数的适用性有所区别,但本研究获得的预测模型可为其他食品热烹饪过程的hfp计算提供一定参考。1.5 hfp的无量纲预测模型的构建


1.6 试验方法




1.7 数据拟合计算
2 结果与讨论
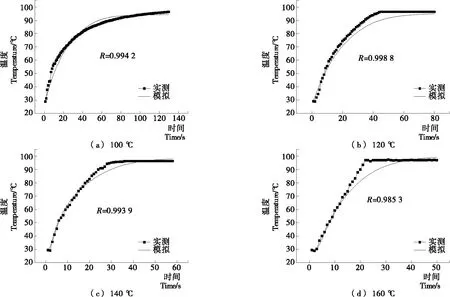
2.1 烹饪流体—颗粒多孔介质热/质传递模型准确性验证与hfp结果
2.2 hfp的无量纲预测模型的拟合与修正

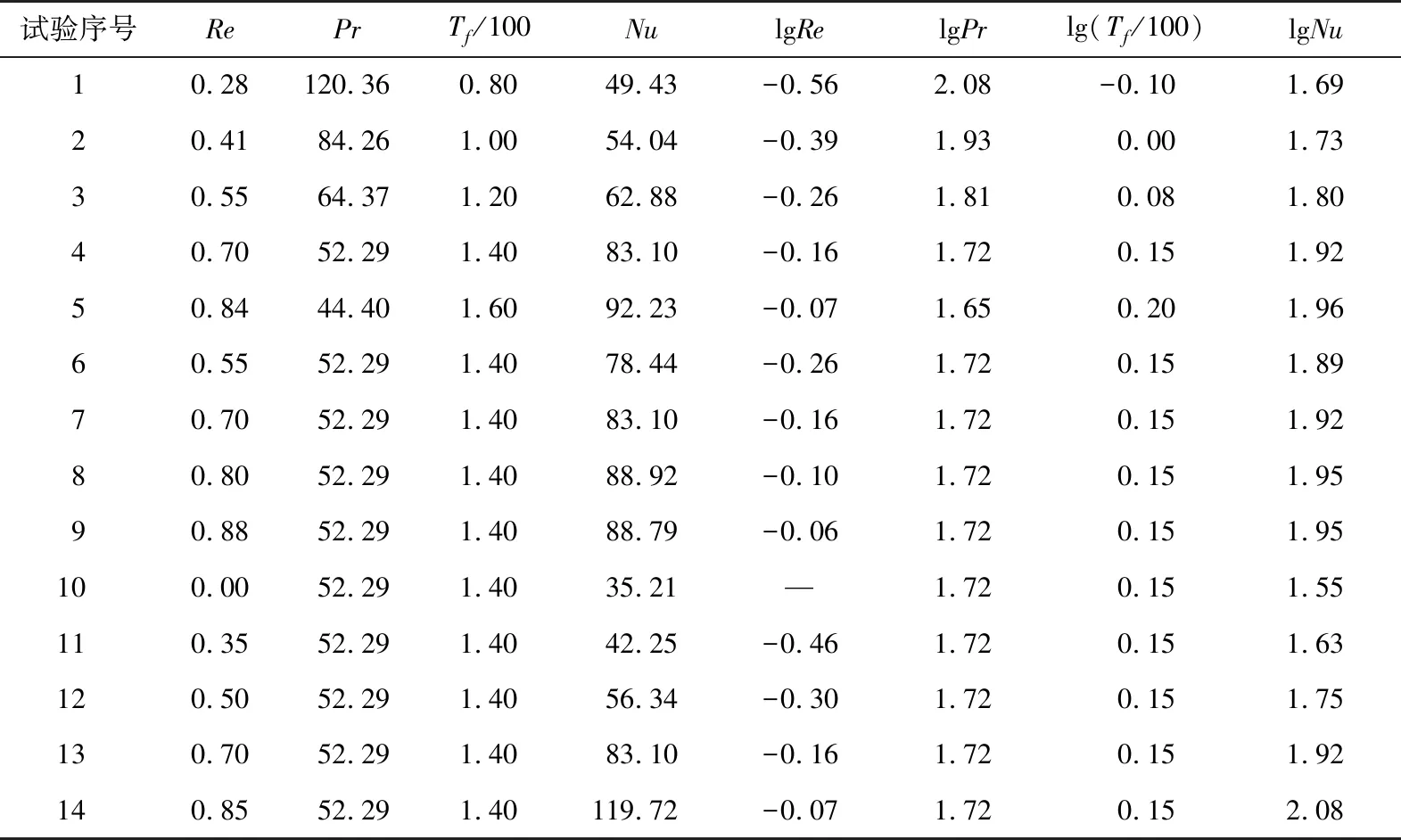

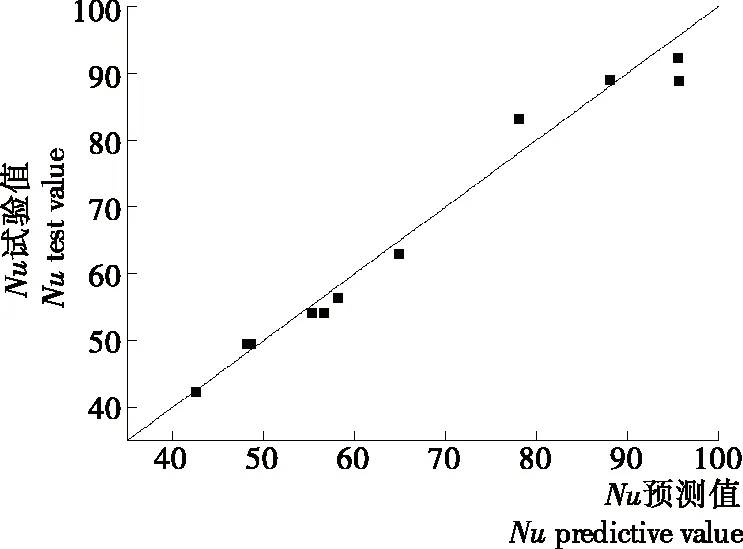
2.3 hfp预测模型准确性验证

2.4 基于量纲分析原理的hfp预测模型的应用
3 结论

