一道解三角形试题的探究与赏析
广东 杨伟达
一、试题呈现
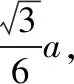
考点分析:本题以三角形为背景,以正余弦定理、三角恒等变换、最值为载体,在正余弦定理、三角函数、不等式等基础知识的交汇处精心设计,本题考查了学生逻辑推理能力、转化与化归能力、运算求解能力.试题背景熟悉,条件简单清晰,表述简洁,对数学知识、思想方法能有效地考查,能较好地甄别学生的数学思维水平和数学潜能,是一道看似平淡无奇,实则内涵丰富的好题.
二、思路探究及解答过程
1.题目已知条件是什么?结论是什么?未知量是什么?尝试用自己的语言表述.
本题已知条件涉及△ABC边BC的高,题设目标求最大值,涉及熟悉的基本不等式结构.
2.思维障碍
本题看似熟悉但又陌生,不少学生看到基本不等式结构就秒杀,其结果是错误的,因为它不是求最小值,而是求最大值,且题目条件仅涉及三角形的高,需要挖掘三角形的隐含条件,不少学生没见过此类题型,一时无从下手,只能望题兴叹.
3.常见相关类型题目及解题思路
有关三角形为背景的题型通常用正余弦定理、三角恒等变换处理,最终回归到函数或三角函数形式处理最值.
解法一(正余弦定理+辅助角公式)
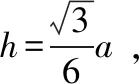
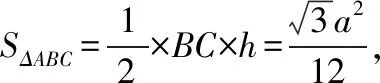
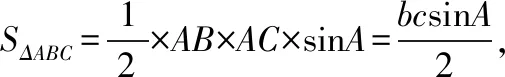
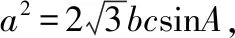
在△ABC中,a2=b2+c2-2bccosA, ④
由③④得b2+c2=4bcsin(A+30°),
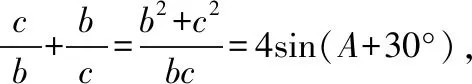
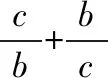
点评:从三角形的面积公式出发,利用正余弦定理、三角恒等变换、辅助角公式,最后利用三角函数的有界性求解. 这种解题过程思路清晰、自然,运算简单,方便求解.
解法二(函数法)
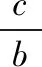
在△ABC中a2=b2(1+x2)-2b2xcosA, ①
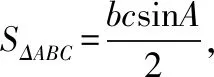
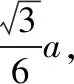
①④联立化简得x2-4sin(A+30°)x+1=0,
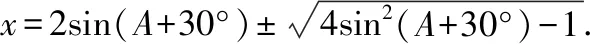
不妨令sin(A+30°)=t,
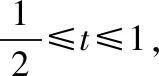
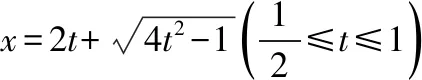
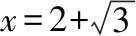
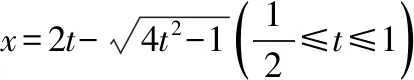
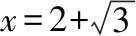
点评:此题转化为对勾函数求最大值时,关键在于求自变量的取值范围,所以必须充分挖掘三角形的隐含条件,结合正余弦定理及三角形面积公式转化为一元二次方程,利用三角函数、导数等知识即可求解.此方法思路虽然简单、自然,但解答过程繁杂,运算量大,不宜提倡.
解法三(坐标法)
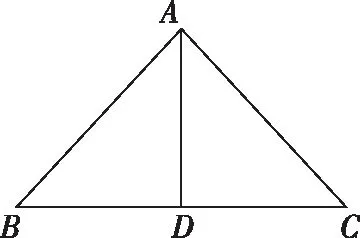
如图不妨令a=6,
以BC连线为x轴,BC的中垂线为y轴建立平面直角坐标系,
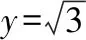
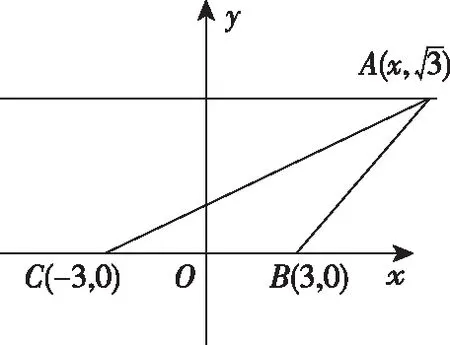
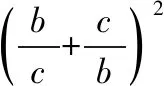
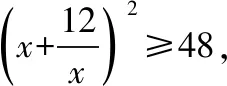
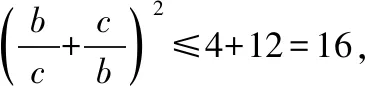
因为b,c>0,
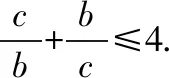
点评:从点的坐标出发,结合两点间距离公式,原式转化为函数关系式,变形后利用基本不等式可将问题解决. 经比较发现,选择B,C为定点,A为动点,以BC连线为x轴,BC的中垂线为y轴建立平面直角坐标系对解题起到方便、快捷的效果.
三、解题后反思
1.丝丝困惑,一一拆解
【困惑1】满足A=60°的△ABC有几个?
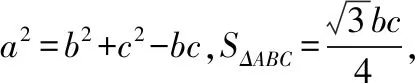
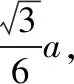
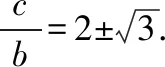
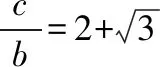
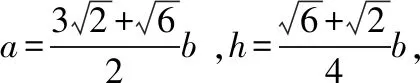
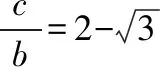
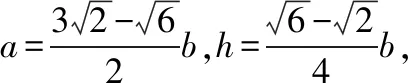
所以像这样满足A=60°的三角形ABC存在2个.
【困惑2】如何求解A的取值范围?
从解法一化简结果4sin(A+30°)分析可知,
在△ABC中,0° 所以30° 由此,△ABC不存在最小值.经检查发现,上述情形是错误的.原因是△ABC中没有考虑角A的取值范围.那么角A的最大角度是多少?如图,当△ABC为等腰三角形时,D为BC的中点,此时角A最大. 所以B=C=30°,A=120°, 所以0° 笔者细心研究发现,原题与2016年高考数学江苏卷第14题的已知条件是等价的,所以原题可转化为: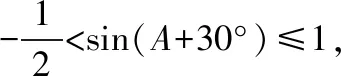
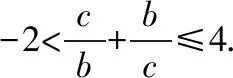

2.等价转化,寻找最佳解法

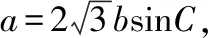
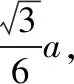
3.小题快做,提高增分意识


