基于Detroit模型和深度学习的交通流调度方法应用分析
顾 洵,李储信
(中国人民公安大学 交通管理学院,北京 100038)
0 引 言
交通系统在人们的日常生活中起着重要的作用,影响一个城市的健康发展[1]。随着各个城市经济的发展,城市中的人口和车辆渐渐增多,城市的交通系统负担越来越重,交通也越来越拥挤,使人们的出行压力增大,所以本文通过调度和控制车辆流解决人们出行的交通拥堵问题。为了舒缓城市交通的压力,增强车辆的通信能力,增强城市交通的运行能力,因此塑造城市交通流的优化调度模型是必要的。
如今研究出很多交通流控制和调度方法解决交通系统拥堵的问题,如文献[2]采用基于POD方法依据Godunov流调度控制交通流,若车道中的车辆密度和线性特征发生变化,调度交通流的有效性和效率均降低。文献[3]采用基于时空图的交通流量统计检测方法,根据城市轨道交通实际运营中交通流数据,以时间和空间两个维度为基础研究城市轨道交通流分布情况,将智能调度交通的各个路网节点,但该方法在交通负载变化比较剧烈时的调度性能较差。文献[4]采用基于层次颜色Petri网的交通紧急调度算法,该算法对交通流数据量要求较高,而且参数设置十分复杂,不易操作。
针对以上问题,本文提出基于Detroit模型和深度学习的交通流调度方法,获取对应道路的最佳交通流,实现交通流的有效调度。
1 基于Detroit模型和深度学习的交通流调度方法应用分析
1.1 基于Detroit 模型的交通需求分布预测方法
通过交通量分布表,即O-D(Origin and Destination Table)矩阵表描述各地区交通发生量和交通吸引量,以O-D矩阵表为基础预测交通流需求分布[5]。建立全国交通流O-D矩阵表是预测交通流需求分布前提条件。
基于Detroit 模型(底特律模型)分析未来交通出行分布相关因素,该因素与出行发生和吸引量的增长率以及出行生成量的增长率息息相关,a-b地区间O-D表的增长系数,随着a地区出行发生量和b地区出行吸引量增长系数之积的增加而变大,但随着出行生成量的增长系数增加而减小,则有:
(1)

(1)设迭代次数z=0;
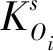
(2)
(3)

(4)
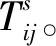
通过以上模型的迭代计算过程计算出预测年的分布矩阵,然后根据部分布矩阵获取预测年的车辆流信息,依据该车辆流采用深度学习模型,获取实际道路交通流,实现城市交通流的优化调度[7]。
1.2 深度学习模型在交通流调度中的应用
1.2.1 深度信念网络
深度信念网络模型(Deep Belief Network,DBN),该模型根据大量限制波尔兹曼机(Restricted Boltzmann Machine,RBM)组合在一起[8]。各个层的RBM均含有隐藏层,并且仅有一个隐藏层,下一层的输入以各个层的输出为基础。在反复的实验中,以Hinton为代表的研究人员得到一种高效率训练的方法,被称作每次训练一层法,该方法每次训练DBN时均可一层一层的训练。
在马尔可夫随机场(Markov random field,MRF)中,限制波尔兹曼机(RBM)是一种特殊的方法。如果一个二分图,所有层的节点与节点没有关联[9],则一层为可视层,另一层为隐藏层,设定各个节点均是采用随机和二值分布方法获取,以概率分布符合波尔兹曼分布为前提,根据对称矩阵连接可视层和隐藏层,得到限制波尔兹曼机(RBM)。通过观察发现它们的状态:可视层和输入相对应、隐藏层和特征相对应,探测隐藏层和特征的组态能量方程(n,m)是:
(5)
其中:ni是输入i,也就是2.1小节获取的预测年车辆流,mj是特征j;bi和aj分别是i和j的偏移量;wij是i和j的权重矩阵。由于各个隐藏层具有相对独立的条件,即:
(6)
如果n或者m是已知的,则n和m的条件概率分布为:
(7)
以给定的一组训练集{Nc|c∈{1,2,…,C}}为基础,将该模型的对数似然函数发挥到极致,如下所示方程:
(8)
通常根据梯度下降法计算得到参数wij,bi和aj,本文采用吉布斯采样法近似获取参数wij,bi和aj,即可视层N通过指定的规则统计得到隐藏层M,然后在反过来统计可视层N,循环多次该过程。可以在可视层和隐藏层的平衡分布中取样[10],因为循环进行迭代时模型会丢掉它的初点。因此,函数期望通过对比分歧(CD)方法在有限次内取得相似值。CD-N视作N+1次采样的算法。实际应用中,一般用CD-1就能够取得合适的值。则以下为权值wij的更新规则:
Δwij=λσ(Cdata[nimj]-Cmod[nimj])
(9)
其中:λσ和Cdata分别是学习速率和当可视层输入时隐藏层的期望输出[11];Cmod是根据CD算法估算的期望输出。则bi和aj的更新规则与wij基本相同:
Δbi=λb(Cdata[ni]-Cmod[ni])
Δaj=λa(Cdata[mj]-Cmod[mj])
(10)
1.2.2 高斯-伯努利 GBRBM
限制波尔兹曼机(RBM)一般情况下,可视层只能代入0或1,不利于模拟类似于交通流这样连续的数据。但是,依据高斯-伯努利(GBRBM)进行现实数据实验模拟,将高斯噪音的连续值加入实验模拟数据中,因此可视层被普通RBM的二进制取代[12],其能量函数改进成如下公式:
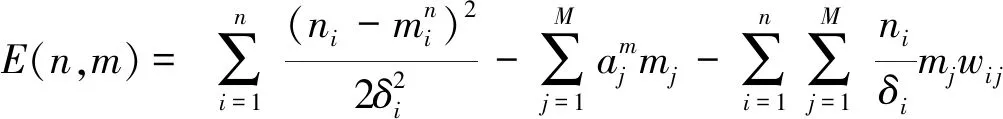
(11)
其中:ni和δ分别为可视层第i个真实值及高斯函数的标准方差。可视层根据以上方程可以最先得到任意特定连续值,通过能量方程,以下是获取的条件概率分布:
(12)
它的训练调度过程和通常的RBM基本相同,都是根据CD过程调节参数。
1.2.3 深度学习模型
深度学习模型是由深度信念网络(DBN)与高斯-伯努利 GBRBM共同建立[13],用于非监督特征学习的基础是由GBRBM和RBM构成DBN的基本架构;将回归层放于顶层,其作用是预测,持向量机(SVM)可以同顶层互换。如图1描述的是深度学习模型。
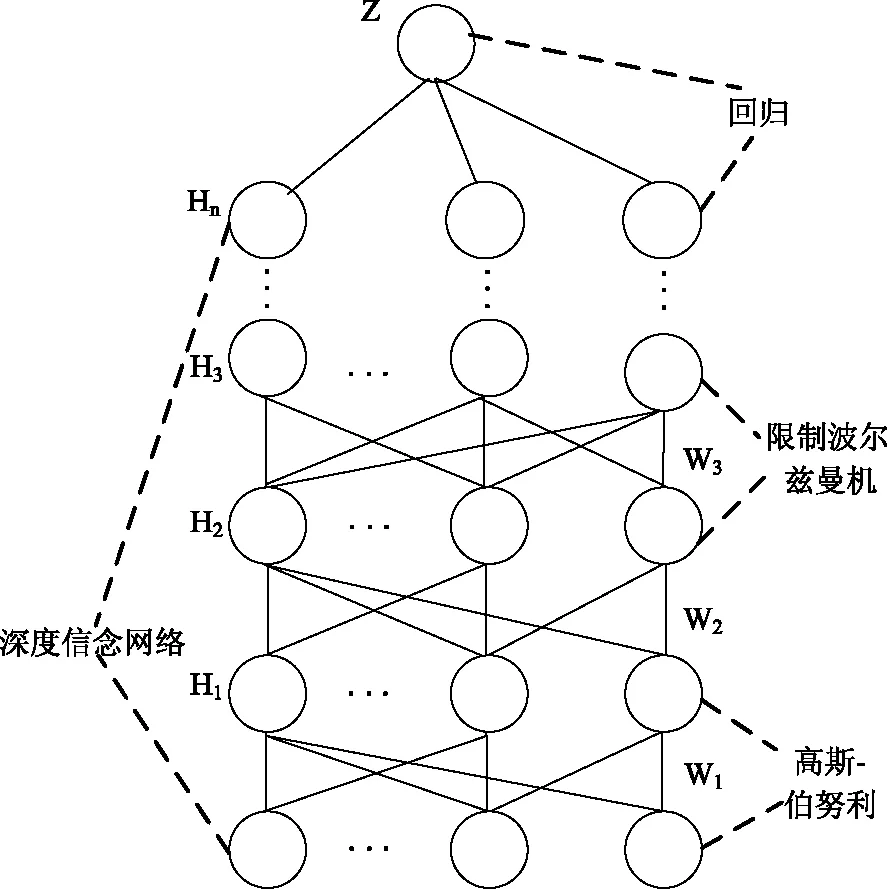
图1 深度学习模型
分析图1可得,当DBN预训练结束后,上层利用有标签的数据,通过BP算法调节参数。该方法比直接用BP算法做梯度下降调整的普通神经网络算法性能优越,主要是因为:通过DBN预训练得到的参数和训练完成的参数非常相似,然后利用BP算法,在所得参数中进行一个局部的搜索[14],训练和收敛的速度都提升很多,下面是深度学习模型进行交通流调度的训练过程:
(1)将2.1小节获取的预测年交通流数据均归一化到[0,1]之间,则输入向量Y为:
(13)

(2)输入用向量Y表示,利用CD过程训练首层GBRBM。
(3)上层RBM的输入则是GBRBM的输出,然后训练RBM。
(4)上层的RBM的输入则是RBM的输出,然后训练RBM。
(5)循环第(4)步,若给定的层数执行完成则停止。
(6)高层回归层的输入则是最终RBM的输出,对其参数依照情势初始化。
(7)采用监督式BP算法调整深度学习模型的参数。
利用训练获得的深度学习模型,在一组输入向量已知的情况下,获取对应道路的实际车辆流。底层数据潜在的典型特征可以通过深度学习模型有效地非监督获取[15],为高层进行分类与回归提供有效地信息,进而有效地进行交通流调度。
2 交通流调度蚁群优化方法
根据深度学习模型获得的实际车辆流输出结果,考虑车辆调度的时间窗问题。采用最大最小蚁群算法对交通流调度进行最优分析。
其总体流程如图2所示:
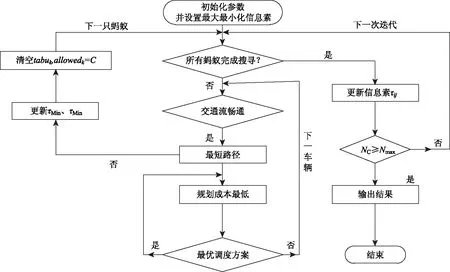
图2 交通流调度蚁群优化流程图

ηij为路段{i,j}的相关程度,也是交通流调度的启发函数,根据车辆的行驶时间的长短该启发函数的表达式如下:
(14)
其中λ1表示单位距离系数,λ2表示单位时间系数,Di代表蚂蚁去往节点i的出发时间,dij代表路段{i,j}的行驶距离,Tij(dij,Di)代表蚂蚁在两个路段节点之间的行驶距离。

(15)
(16)
τij(t+ε)=(1-ρ)τij(t)+Δτij(t)
(17)
信息素的强度值为Q,Lk为蚂蚁k在循环路段中的路径总长,ρ为蚂蚁的信息素挥发系数(0<ρ<1),ε为经历一个循环时的时间。
设置最小和最大信息素[τmin(t),τmax(t)]在所有道路上的t时的浓度区间,可知最大最小信息素为:
(18)
Lmin(t)为当前交通流调度方案中的最短总距离,即为当前调度方案的最优解。
3 实验分析
3.1 吞吐量分析
为了验证方法在交通流调度方面的有效性,采用MWorks对所所提方法进行调度仿真,MWorks软件是一种多领域通用的CAE平台软件,集合系统工程建模、仿真和分析于一体,能够达到可视化分析,保障分析结果的完整功能基础上,支持多目标优化和多平台联合仿真。通过仿真实验检验本文方法进行交通智能调度的效果,实验设置0°~90°为方位角度的变化范围,并且以坐标(0,0,0)作为预测车辆信息监控中心方位坐标,在交通系统中,将重要枢纽、车站码头和交通路口做无向图规划,182,287,291和341作为路网相交路口节点数目。城市交通流调度和控制系统参数用表1描述。

表1 交通控制系统的参数
以表1的参数为基础,构建交通调度仿真实验,设定交通路网路段的流量是路段通行能力的10%,利用本文方法获取交通流密度参量和特征信息,通过该信息完成交通流优化调度,获得交通流中车辆的吞吐率。将路网通行能力作为检验标准,验证本文方法、平均增长系数法和Fratar法在调度交通流时耗费的吞吐量,结果用图3描述。
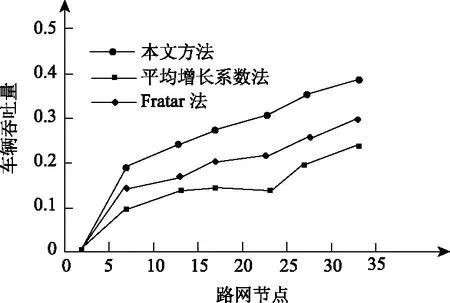
图3 不同方法车辆吞吐量比较
分析图3可得,采用本文方法的交通路网吞吐量高于平均增长系数法和Fratar法,采用本文方法得到的车辆吞吐率最高可达到0.4,平均车辆吞吐率达到0.26,采用平均增长系数法和Fratar法获得的车辆吞吐率最高分别是0.2和0.28,利用本文方法得到的车辆吞吐率比平均增长系数法和Fratar法得到的车辆吞吐率分别高出0.2和0.12。说明利用本文方法能有效的提高城市交通通行能力,提高路网中车辆的吞吐量。
3.2 离散度和规划误差分析
采用本文方法、平均增长系数法和Fratar法(福莱特法)进行交通流调度实验,比较3种不同方法进行交通流调度的离散度和规划误差,对比结果见图4和图5。

图4 不同方法离散度比较

图5 不同方法的规划误差比较
分析图4和图5得出,采用本文方法对公共交通路网中车流量调度的最低离散度仅为3.8%,平均离散度为5.4%,采用平均增长系数法和Fratar法的最低离散度分别为30%和90%,平均规划误差分别为45.3%和94.5%。利用本文方法对公共交通路网中车流量调度的平均离散率比利用平均增长系数法和Fratar法的平均离散率低39.9%、89.1%。
采用本文方法对公共交通路网中车流量调度的最低规划误差仅为5%,平均规划误差为8.5%,采用平均增长系数法和Fratar法的最低规划误差分别为20%和90%,平均规划误差分别为25.2和92.5%。利用本文方法对公共交通路网中车流量调度的平均规划误差比利用平均增长系数法和Fratar法的平均规划误差低11.5%、81.5%。
这些数据结果说明,利用本文方法对交通流的调度效果好、规划精度高,有效提高城市交通的管理质量。
3.3 调度时间和调度效率分析
利用本文方法、平均增长系数法和Fratar法进行智能交通调度实验,获得三种方法耗费的调度时间,结果如图6所示。
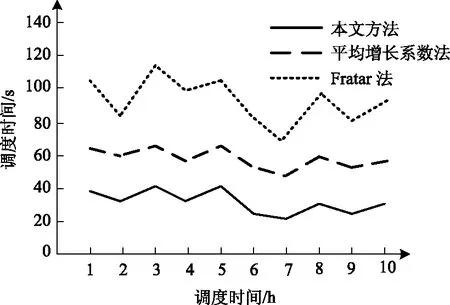
图6 不同方法的调度时间对比结果
分析图6可得,在对智能交通调度过程中,本文方法耗费的交通流调度时间最低为22 s、最高为41 s,平均调度时间是31.5 s;而平均增长系数法和Fratar法耗费的最低调度时间分别为53 s和76 s,最高调度时间分别为68 s和113 s,两种算法的平均调度时间分别是60.5 s和94.5 s;说明采用本完方法可以大大较少交通调度时间。
图7为利用本文方法、平均增长系数法和Fratar法进行智能交通调度实验,获得交通调度效率情况。
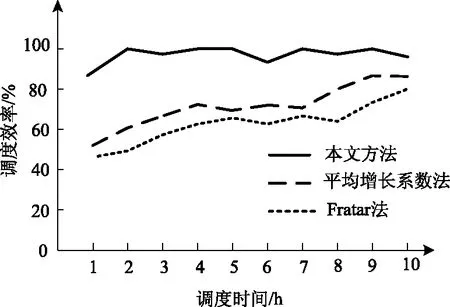
图7 不同方法的调度效率对比结果
分析图7可得,在进行智能交通调度过程中,采用本文方法对交通流的调度效率最高达到99.8%,平均调度效率为91%,采用平均增长系数法和Fratar法对交通流的调度效率最高为85%和78%,平均调度效率分别为76%和65%,采用本文方法对交通流的调度效率远远高于其他两种方法,因此利用本文方法能够高效率进行交通调度,具有较高的应用价值。
4 结 语
交通分布预测是交通流调度的基础,本文采用基于Detroit模型和深度学习的交通流调度方法,采用Detroit 模型对交通需求分布预测分析,得到预测年车辆需求分布情况,依据该结果采用深度学习模型,获取不同道路的实际车辆流,实现交通流的优化调度。仿真实验说明,在智能交通调度过程中,运用本文方法能够提高路网车辆的吞吐量,吞吐率可以达到0.4,本文方法的平均交通流调度时间仅为31.5 s,调度效率最高达到99.8%,本文方法对公共交通路网中车流量调度的平均离散度为5.4%,平均规划误差为8.5%,这些数据结果说明本文方法具有较高的交通流调度性能。

