基于网络演算的1553B总线延迟上界计算方法

陈克伟, 宋小庆，廖自力，石海滨

(陆军装甲兵学院 兵器与控制系,北京 100072)

0 引 言

1553B总线的应用领域大多在各种军事作战平台上，系统运行强调高度的安全、可靠和稳定[1-2]。为了满足特定实时性要求的1553B总线系统设计，传统方法(如排队论、随机Petri网理论等)大多对系统的性能指标进行近似评估，但是系统中存在着一些安全关键性消息，这些消息特别强调在最坏情况下的延迟时间。

对于1553B总线的性能指标分析与评价，国内外研究者做了一些尝试性工作：文献[3]利用排队论建立1553B总线非周期消息的M/M/1排队模型,分析了1553B总线的平均响应时间和总线利用率等性能指标；文献[4]使用随机Perti网分析了车载1553B总线的总线负载等性能指标；文献[5]、文献[6]和文献[7]分别以确定与随机Petri网为工具分析了1553B总线的平均延迟时间等性能指标；文献[8]和文献[9]利用有色Petri网的分层建模机制建立了1553B总线的分析模型，分析了1553B总线的总线负载和总线效率；文献[10]以OPNET软件为仿真平台，分析了1553B总线的总线负载和延迟时间等性能指标；上述文献的研究视角大多是研究1553B总线平均意义上的统计性能指标，没有研究每个消息在最坏情况下的延迟上界。

网络演算[11]可以用于计算总线网络在最坏情况下的延迟上界。文献[12]采用网络演算理论研究计算了船载CAN总线和以太网的延迟上界；文献[13]采用网络演算理论研究计算了民用汽车CAN总线的延迟上界；文献[14]采用网络演算理论研究计算了军用车载CAN总线的延迟上界；文献[15]采用网络演算理论研究计算了AFDX网络的延迟上界；文献[16]采用网络演算理论研究计算了TTP总线流量调度机制及其实时性；文献[17]采用网络演算理论研究计算了改进的TTE网络RC流量延迟上界;文献[18]采用网络演算理论研究计算了AVB网络的端到端的延迟上界；综上可知，网路演算理论在各个领域的总线网路的延迟上界分析中得到了广泛的应用。文献[19]和[20]用网络演算研究了1553B总线的延迟上界，但是文献[19]假设每个消息携带16个数据字，文献[20]假设每个消息携带32个数据字，可以看出文献[19]和[20]对每个消息携带的数据字都做了简化假设，并没有考虑各个消息的数据长度对延迟上界的影响；另外，文献[19]和[20]假设系统中最长的消息为携带32个数据字的一个远程终端到另外一个远程终端的消息格式，即消息在最坏情况下的等待时间为0.75 ms，可以看出这种简化假设没有考虑系统设计之初所要传输的消息集合是确定的前提。为此，本文综合考虑每个消息的优先级、数据长度、发送周期及最长消息的数据长度取值对1553B总线延迟上界的影响，提出一种新的基于网络演算的1553B总线延迟上界计算方法。

1 1553B总线分析

图1 1553B总线拓扑结构

如图1所示为1553B总线单级拓扑结构，该结构由一个总线控制器(Bus Controller, BC),N(1≤N≤31)个远程终端(Remote Terminal, RT)组成[1]。1553B总线中，每个消息都有相应的优先级和发送周期。此外，1553B总线协议中有10种不同的消息格式，每种消息格式的传输时间由于不同的传输需求(即所要传输的数据字的个数从1到32不等)是大小不一样的，因此，在求解1553B总线延迟上界的时候就要综合考虑每个消息的优先级、发送周期和数据长度等因素。

2 网络演算预备知识

2.1 到达曲线

定义1 到达曲线。令F是广义增函数集合[11，14]，给定一个函数α(t)∈F，若有数据流(Data flow, DF)的输入累积函数为A(t)，当且仅当对于所有0≤s≤t满足式：

A(t)-A(s)≤α(t-s)

(1)

则称A(t)是被α(t)限制的，α(t)被称为A(t)的到达曲线。

α(t)用来约束进入总线中DF，通常使用漏桶模型：

αr,b(t)=b+rt

(2)

其中：r表示DF的平均速率，b表示DF的突发容忍度。如图2所示，用到达曲线α(t)限制DF的输入累积函数A(t)，即用α(t)表示A(t)的上确界。

图2 到达曲线和漏桶模型

定义2 最小加卷积运算。最小加卷积运算定义为：

(3)

其中∀f,g∈F，inf{}为求下确界运算。

应用定义2中式(3)，则式(1)中到达曲线α(t)和DF的输入累积函数A(t)的关系可以表示为：

A(t)≤(A⊗α)(t)

(4)

2.2 服务曲线

定义3 服务曲线。给定一个系统S和一个DF的输入累积函数A(t)，B(t)记为DF通过系统S后的输出函数，对于函数β(t)∈F,β(0)=0，当且仅当满足式：

B(t)≥(A⊗β)(t)

(5)

则称系统S为DF提供了服务曲线β(t)，而(A⊗β)(t)表示在给定DF输入累积函数为A(t)时DF的输出函数B(t)的下确界。

服务曲线用来表示总线所能提供给DF的最小服务保证, 通常使用速率延迟模型：

βR,T(t)=R·[t-T]+=R·max{t-T,0}

(6)

其中：R表示总线的最小服务速率，T表示总线的最差延迟时间，如图3所示。[t-T]+=max{t-T,0}表示取值为t-T和0中的最大值，具体地，当t-T≥0时，取值为t-T；当t-T≤0时，取值为0。

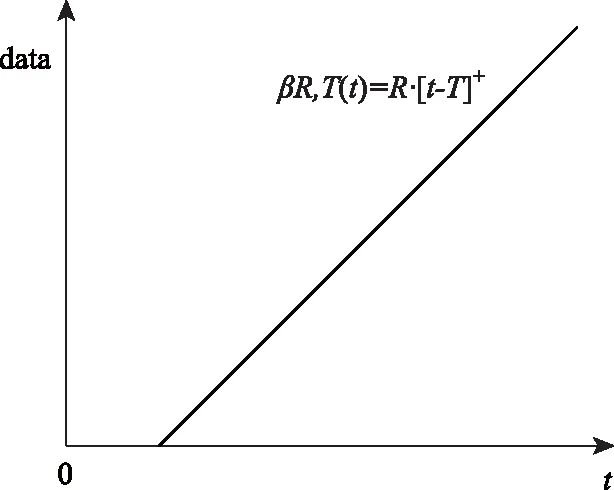
图3 速率延迟模型

2.3 延迟上界

定理1 延迟上界。假设一个系统S可以为DF提供的服务曲线为β(t)，若有一个DF的到达曲线为α(t)通过系统S时，其延迟上界D(t)满足如下关系：

(7)

其中：d表示到达曲线α(t)和服务曲线β(t)之间的水平距离，sup{}为求上确界运算。

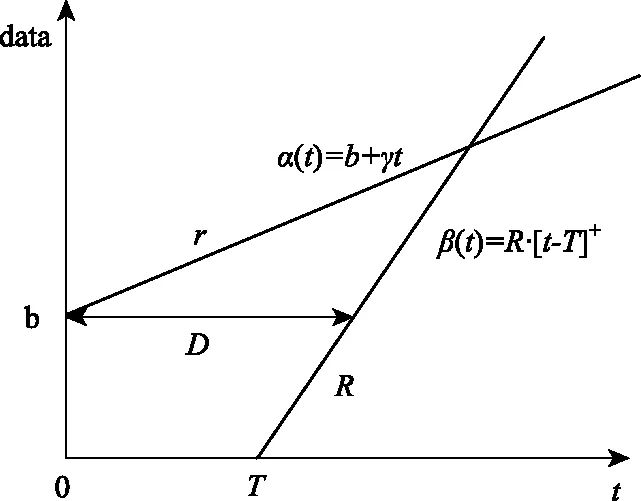
图4 延迟上界

如图4所示，假设DF的到达曲线为α(t)=b+rt，总线的服务曲线为β(t)=R·[t-T]+。由定理1中式(7)可以推理得到该总线的延迟上界D，即图4中到达曲线α(t)与服务曲线β(t)的最大水平距离。

3 1553B总线延迟上界计算方法

3.1 1553B总线到达曲线模型

假设某1553B总线系统有N个消息，优先级大小依次为0～N-1。为便于推导计算优先级为i(0≤i≤N-1)的消息Mi的延迟上界，这里将全体消息分为三类集合：第一类消息集合为{Mi}，即消息Mi自身；第二类消息集合为{M0,M1,…,Mi-1}，即优先级高于消息Mi的消息全体；第三类消息集合为{Mi+1,Mi+2,…,MN-1}，即优先级低于消息Mi的消息全体。由于消息Mi必须等到优先级高于Mi的消息全体发送完后，才能使用总线，可知第三类消息集合对于消息Mi的延迟上界不产生任何影响，因此可以忽略不计。

假设消息Mi的发送周期为Ti，数据长度为li，则消息Mi输入累积函数为：

αi(t)=[t/Ti]·li

(8)

由定义1中式(1)和式(2)可令消息Mi到达曲线为：

(9)

则消息Mi突发容忍度bi=li，平均速率ri=li/Ti。

由式(8)推导优先级高于消息Mi的消息集合的输入累积函数为：

(10)

由式(9)推导优先级高于消息Mi的消息集合的到达曲线为：

(11)

3.2 1553B总线服务曲线模型

1553B总线系统的通信速率为RC=1 Mbps，最长消息的数据长度为lm=max{l0,l1,…,lN-1}，因此，在最坏情况下消息Mi的等待时间为：TC=lm/RC。

由定义3中式(5)和式(6)可令1553B总线的初始服务曲线为：

β0(t)=RC·[t-TC]+=max{RC·(t-TC),0}

(12)

又因为消息Mi必须等待全部优先级高于Mi的消息发送后，才能使用总线，因此消息Mi的服务曲线为：

(13)

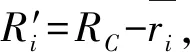
3.3 1553B总线延迟上界计算

由定理1中式(7)得消息Mi的延迟上界为：

(14)

又由式(11)和(13)推导得：

(15)

4 仿真实验

表1给出了某车载1553B总线系统中的每个消息Mi的优先级i、消息格式及相应的数据字个数、数据长度li和发送周期Ti(0≤i≤4)。那么可以计算得到：lm=max{l0,l1,l2,l3,l4}=260 bits。

表1 消息参数

表2 1553B总线消息的延迟上界计算结果

图5 消息的最大延迟

与相关研究相比，本文所提方法具有如下优点：

(1)综合考虑了每个消息的优先级、数据长度、发送周期及最长消息的数据长度取值对1553B延迟上界的影响，因而具有更好的普适性。

(2)模型参数少，计算量小，可快速计算1553B总线中每个消息的延迟上界。

(3)在平台系统设计之初，可以根据工程的技术指标提前计算1553B总线中每个消息的延迟上界，使得设计满足平台系统严格的实时性要求。

5 结 语

本文提出一种基于网络演算的1553B总线延迟上界计算方法，建立了1553B总线的到达曲线模型和服务曲线模型，并推导出1553B总线延迟上界的计算表达式。本文方法综合考虑了1553B总线中各个因素对其延迟上界的影响，因而具有更好的普适性。仿真实验验证了本文方法的有效性，该方法可以快速求解有效地求解1553B总线中每个消息的延迟上界。本文的研究为1553B总线的分析、设计与优化提供了一种新的思路与方法。

下一步将研究1553B总线、CAN总线和MIC总线等几种不同总线互联情况的延迟上界计算方法。