一种适合FPGA实现的低错误平层比特翻转算法
马克祥
(中国电子科学研究院,北京 100041)
0 引 言
由于LDPC码具有逼近香农限的良好译码性能,进而得到了广泛的研究[1],并且被广泛应用于现有的一些主要通信系统中,比如5G、10Gbit Ethernet(IEEE 802.3an)等其它通信系统。LDPC码作为一种具有并行译码结构的线性分组码,尤其适合利用FPGA等并行计算平台构造并行编译码器实现快速译码[2-3]。为了获取更好的译码性能,LDPC码的各种译码算法得到广泛研究。其中,对于光通信等超高速数据传输场景,比如工作在40 Gb/s的下一代光纤通信系统,现有的硬件水平只能支持实现BF-based译码器[4]。
由于BF-based算法在译码速度方面固有的优势,因此得到广泛的研究。通过给不同的校验方程引入不同的可靠性度量值,加权比特翻转算法(Weighted BF,WBF)首先被提出来改进BF算法的译码性能[5]。Zhang利用每个比特的信道接收值对WBF算法的品质因素进行修正,进而提出Modified WBF (MWBF) 算法[6]。上述算法表现出良好的译码性能,具有良好地应用前景。不过,定点仿真试验结果表明,WBF和MWBF算法的译码过程中会出现“伪零值”现象,使得算法利用FPGA平台实现时将会出现性能恶化的结果。为此,本文给出一种修正的加权比特翻转算法解决上述问题,从而保证LDPC码利用FPGA平台进行加权比特翻转译码时可以获得良好的译码性能,实现相应码字的快速译码,从而满足高速数据传输系统的快速译码需求。
1 WBF算法伪零值现象分析

翻转函数的计算尤为关键。翻转函数值的大小决定着比特是否翻转,比特的正确翻转直接决定译码是否正确。WBF算法的翻转函数计算公式如式(1)所示[5],本节以WBF算法为例详细阐述算法精度问题。
WBF算法计算翻转函数的公式:
(1)
wm是一个非负实数,sm的取值为0或者1,单比特翻转每次翻转最大函数值对应的比特,所以翻转函数值越大,对应比特被翻转的可能性越大。下面将详细分析WBF翻转函数公式:
(1)假定wm>0,m∈A(n)。如果第eWBF,n比特参与的所有校验式均为0,则该比特出错概率很低,易知eWBF,n是一个较大的负数,第eWBF,n比特被翻转的可能性极低;如果第eWBF,n比特参与的校验式中有多个校验式值为1,该比特出错的概率较高,易知eWBF,n是一个较大的正数,第wm=0比特被翻转的可能性高。
(2)假定wm=0,m∈A(n)。译码过程中,如果第eWBF,n比特正确,其对应的翻转函数值eWBF,n值为0。如果第eWBF,n比特错误,不论有几个校验式值(第eWBF,n比特参与的校验式)为1,eWBF,n值均为0,而且在迭代译码过程中,无论该比特是否翻转,其对应的翻转函数值始终为0。此时,无法区分eWBF,n的0值是由哪种情况导致的,若翻转了该比特极有可能导致译码出错。本文将发生在WBF译码过程中,由wm=0造成的译码混淆称为“伪零值”现象。
2 改进加权比特翻转算法
由前述分析可知,WBF算法译码过程中出现的“伪零值”现象使得比特节点的品质因素无法利用每次迭代的校验信息进行正确的更新演化,即zn=(1-sgn(yn))/2取不同值时,若zn=(1-sgn(yn))/2将会导致zn=(1-sgn(yn))/2的值始终为0,进而影响该比特节点的翻转译码,甚至导致整个码字的译码失败。因此,本文通过限定校验可靠度最小值的方式消除“伪零值”现象。改进算法具体描述如下:
Step1:k=0;对于每个变量节点计算初始硬判决值zn=(1-sgn(yn))/2。利用式3-1计算每个校验节点m的品质因素值。
(2)
Step2:计算伴随向量重量ηk,如果ηk=0,停止译码并且输出zk。
Step3:k=k+1。如果zk,译码失败并且输出zk。
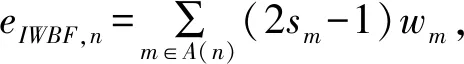
(3)
Step5:翻转具有最小品质因素的变量节点,然后转到Step2。
3 仿真分析
本节对WBF算法以及本文提出的改进加权比特翻转算法(Improved Weighted Bit-Flipping, IWBF)的仿真性能进行比较分析。仿真使用的码字分别为:EG(273,191)和EG(1023,781)码,为了方便后续描述分别简记为码1和码2。测试数据经过BPSK调制后经由AWGN信道传输。译码器的最大迭代次数为100。每个SNR点观察到100帧错误数据停止译码性能统计。
图1和图2分别给出码1和码2,在WBF、WBF(hard)以及IWBF(hard)算法下译码性能比较。WBF(hard)和IWBF(hard)算法为定点仿真,整数部分量化比特固定为5。对于定点仿真,分数部分精度是影响译码性能的关键因素。本文给出算法在3、5和7比特量化精度的性能比较。由图1可知,WBF译码时,码1的误码率小于10-5且未出现错误平层,IWBF(hard)算法在5和7比特量化精度的情况下获得与WBF算法浮点仿真相当的译码性能,3比特量化精度的情况下IWBF(hard)算法译码性能约为10-4与比5和7比特量化相比有将近一个数量级的损失。相同仿真条件下,WBF(hard)在3、5和7比特量化精度场景下,在信噪比为5dB时的译码性能分别为10-2、10-3和10-4。值得注意是,3比特量化精度的情况下IWBF(hard)算法译码性能约为10-4,但是算法在5 dB时并没有达到译码性能的极限,从仿真图可以看出随着信噪比的增大,算法的译码性能仍可以得到进一步的改善,而在3、5和7比特量化精度场景下WBF(hard)都在5 dB时出现较为明显的错误平层。码2利用WBF、WBF(hard)以及IWBF(hard)算法译码性能表现相近,其利用本文所提IWBF(hard)算法在5和7比特量化精度的情况下获得与WBF算法浮点仿真相当的译码性能,且3比特量化精度的情况下IWBF(hard)算法译码性能在4.5 dB时约为10-3,并未出现WBF(hard)译码时的错误平层。图1和图2的仿真结果验证了所提算法的有效性。另外,在具体工程实现时,对于码1和码2建议使用5比特量化精度实例化LDPC译码器,在硬件开销较小的情况下获得接近于WBF算法的译码性能。

图1 码1不同算法译码性能比较

图2 码2不同算法译码性能比较
4 结 语
为解决传统WBF算法FPGA实现时出现的性能恶化现象,本文提出一种改进加权比特翻转算法解决WBF译码过程出现的伪零值现象,从而有效降低LDPC码字比特翻转译码时的错误平层。仿真结果表明,利用本文算法可以有效解决加权比特翻转算法性能恶化现象。对于码1和码2,使用5比特量化精度实例化LDPC译码器,在硬件开销较小的情况下获得接近于WBF算法的译码性能。

