基于PCR5规则的非合作目标识别方法研究

李 洋，卓志敏，张 南，张丹丹

(北京电子工程总体研究所，北京 100854)

0 引 言

多传感器信息融合技术相对于单传感器技术可以获得更加准确的目标状态和战场态势等信息，因此受到科研人员越来越多的重视。但是现代化军事对抗过程中，由于战场环境不断变化，同时存在大量噪声、欺骗等干扰使得多传感器获取的信息具有高度的不确定性，需要理论工具对多传感器信息进行准确、稳定、可靠的融合。Dempster-shafer (DS) 证据理论是Bayesian概率理论的一般形式。相对于传统的概率论，DS证据理论具有无需先验信息也可以区分不确定信息的能力，这种优势使得DS证据理论能够提高融合系统的分辨能力和可靠性[1, 2]。在D-S证据理论中，证据的合成规则(Dempster 规则)是理论中最为重要的环节，Dempster规则多适合于融合高置信度、低冲突的证据。但是在复杂的战场环境中，往往会出现冲突程度比较高的证据。直接使用Dempster 融合规则对低置信度、高冲突证据组合则会产生与直观相悖的不合理现象[3-4]。

与直接应用合成规则不同，比例冲突再分配(PCR)规则是将证据中的冲突信度按照一定比例关系分配到证据的非空集合部分。PCR规则可以分为三个步骤进行：首先利用合成规则计算证据的合成信度，然后分别计算局部和全部的冲突信度，最后按照不同的比例将冲突信度分配到非空证据集合中。PCR本质上是利用某种比例将冲突信度分别分配到合成信度上，从而消除冲突证据的影响。PCR规则可以分为PCR1～6，其中PCR5分配部分冲突质量到那些对部分冲突产生影响的元素，满足准结合定律，是数学意义上最精确的比例冲突再分配规则[5]。

本文首先简要的介绍D-S证据理论的基础知识，在第三节给出PCR5定义和基于PCR5融合算法的多传感器信息融合步骤和流程。最后利用不同冲突算例证明算法的有效性和对不同程度冲突证据融合的稳定性。

1 D-S证据理论

D-S证据理论由A. P. Dempster在1967年首次提出的，后经G. Shafer改进推广使之成为了有限离散信息领域中推理的形式。D-S证据理论可以看成经典Bayesian概率理论的推广形式，可以更加灵活的表示未知和不确定的信息，并已经成为了一种更加适合多源传感器数据融合的不确定推理方法[6]。

我们假设集合Θ中有N个事件，分别对应N个可识别的对象或元素。集合Θ满足互斥且完备性，我们称集合Θ为辨识框架。辨识框架的幂集是由集合Θ所有子集组成的，可以表示为P(Θ)。幂集P(Θ)由2N个元素组成，具体表示为：P(Θ) =(Ф, 1, 2,……, (1, 2), (1, 3),……, (N-1,N), (1, 2, 3), ……, Θ)，其中Ф表示空集。

定义1：假设Θ是辨识框架。函数mΘ: 2Θ->[0,1]被称为辨识框架Θ的基本信度指派(BBA)，如果mΘ满足如下条件：

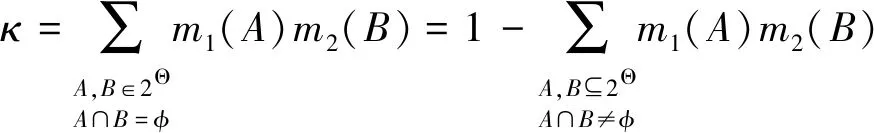
mΘ(φ)=0;

0≤mΘ(A)≤1

(1)

其中2Θ表示辨识框架Θ的幂集，是由辨识框架∪运算的所有子集。

定义2： 给定辨识框架Θ上的BBA，信任函数Bel: 2Θ->[0,1]定义为：

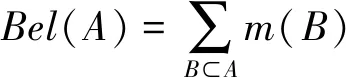
(2)

其中m(A) > 0，A称为信任函数Bel的焦元(focal elements)。

将BBA函数视为概率理论中的概率密度函数的推广形式，同时信任函数可以视为概率分布函数的推广形式，便于理解。在相同的辨识框架下，由两个独立的信息源得到的两个BBAs函数可以使用D-S理论中的Dempster合成规则进行分析，并合成为一个BBA函数，为战场决策和判断提供支撑。主要如下定义。

定义3：在同一辨识框架下，m1和m2分别为信任函数Bel1和Bel2的BBAs函数。对于辨识框架Θ的所有非空子集X的BBA函数m12定义为：

(3)

其中：

(4)

因子κ是辨识框架Θ上的BBA函数，可以表示为Bel1和Bel2的直和(κ=Bel1⊕Bel2)。因子κ可以度量BBAs函数m1和m2之间冲突程度。κ的数值与BBAs函数冲突的大小成正比。当κ=0时，表示待融合的证据之间没有任何冲突，完全相互支持；当0<κ<1时，表示待融合的证据之间有一定的支持度，可以互相融合；当κ=1时，表示待融合的证据间完全冲突，此时不能使用Dempster合成规则进行证据合成。

使用Dempster合成规则进行证据合成过程中，会产生与直观相违背的结果。我们通过下面的例子进行说明。

例1：对于辨识框架Θ={θ1，θ2，θ3}，任意取两个0,1之间正数ε1，ε2。证据E1和E2对应的BBAs函数为：m1(θ1) =1-ε1，m1(θ2)=0，m1(θ3)=ε1;m2(θ1)=0,m2(θ2)=1-ε2,m2(θ3)=ε2。

利用方程(3)可以得到融合的结果为：m12(θ1)=0,m12(θ2)=0,m12(θ3)=1。显然上面的例子与我们直观的判断相违背的，特别是当ε1趋于零的时候，证据E1和E2对于θ3的合成后结果趋于零，融合的结果正好相反。通常证据理论中所产生的悖论是由证据间的冲突或不一致性造成的，需要研究消除证据间冲突的方法。

2 基于PCR5的识别信息融合

在证据高度冲突下实现多传感器信息有效融合是多传感器信息融合必须要解决的问题。Dezert和Smarandache等学者在2002年提出了DSM理论。DSM理论将证据冲突焦元看成有用信息而保留，作为融合成分, 这样从根本上解决了证据理论不能解决证据强冲突的问题[7]。

定义4： 假设_是辨识框架。函数mΘ:DΘ->[0, 1]被称为辨识框架Θ的广义基本信度指派(gBBA)，如果mΘ满足如下条件：

mΘ(φ)=0;

0≤mΘ(A)≤1

(5)

其中DΘ表示辨识框架Θ的超幂集(也称为Dedekind晶格)。方程(1)中幂集是辨识框架包括∪运算的所有子集，而超幂集是辨识框架包括∪和∩运算的所有子集。

在给定辨识框架Θ上的gBBA情况下，广义信任函数gBel也与DS理论Bel定义类似，区别在于广义信任函数gBel是由集合超幂集DΘ到区间[0, 1]的映射。这样基于DSM理论，BBAs的m1和m2在同一识别框架中产生的全局冲突BBA为：

(6)

超幂集可以理解为概率率和DS理论的全面和直接内涵的延伸。比较直观的说明他们的区别如：设Θ=θ1，θ2，利用概率角度BBA满足m(θ1)+m(θ2)=1；DS理论框架下BBA满足m(θ1)+m(θ2)+m(θ1∪θ2)=1；而根据DSM理论可以得出m(θ1)+m(θ2)+m(θ1∪θ2)+m(θ1∩θ2)=1。

对冲突信息的处理通常有两种方式：一是认为Dempster合成规则本身没有造成悖论的产生，而是由证据源造成的，在融合前对数据源进行预处理。二是修改证据的合成规则，适当的分配证据间的冲突成分[8]。而PCR规则从第二种冲突处理方式入手，很好的解决了冲突分配问题。DSmT主要包含了6种PCR规则，分别为PCR1～PCR6，将BBA冲突按照一定比例关系分配到非空集部分中。PCR规则可应用在Shafer和DSm模型下，它既可以处理静态融合问题，也可以处理动态融合问题。由于对冲突进行了再分配，因此这几种PCR规则中的组合信度都设置为0。在PCR规则中，当前公认的分配精度最高的是PCR5，在许多实际应用中PCR5也都是首选。

将BBA函数视为概率理论中的概率密度函数的推广形式，同时信任函数可以视为概率分布函数的推广形式，便于理解。在相同的辨识框架下，由两个独立的信息源得到的两个BBAs函数可以使用D-S理论中的Dempster合成规则进行分析，并合成为一个BBA函数，为战场决策和判断提供支撑。主要如下定义。

定义3：在同一辨识框架下，证据m1和m2分别为信任函数Bel1和Bel2的BBAs函数。对于辨识框架Θ的所有非空子集X的BBA函数m12定义为：

(7)

其中：

(8)

PCR合成规则从第二种方式产生的解决冲突的方法，由Smarandache和Dezert等首先提出，并已经发展了PCR1～6等6种按比例再分配冲突的改进融合规则，其中的PCR5规则按比例将冲突信息再分配到非空焦元上，是目前最为常用的冲突分配方法。

对于两个证据源的融合，PCR5可按如下的合成规则进行融合：

(9)

多传感器对目标进行识别或者对战场态势进行评估，每个传感器会生成针对目标的BBA函数。由于战场的复杂性和各个传感器性能区别，对于目标特征识别通常会产生冲突。对于完全不含有冲突或者含有冲突的多传感器BBAs进行基于PCR5理论的信息融合操作如下面步骤执行：

步骤1：定义辨识框架Θ，将可能出现框架元素全部加入其中；

步骤2：利用多传感器手段，对目标或战场信息进行获取，并分配基本的BBA。BBA函数的数值反映了证据源对目标在辨识框架内元素匹配程度的推理，是传感器的初级判断。不同先验信息对影响到传感器对目标识别的判断，而判断结果又决定了多传感器信息冲突程度的大小；

步骤3：利用PCR5规则对各传感器目标分配的BBAs函数进行冲突估计，并根据PCR5规则进行冲突信息再分配，将冲突信息分配给初步融合后的BBAs结果，进而得到各传感器对目标识别的BBAs函数更新；

步骤4：跟踪PCR5融合后的BBAs函数对目标识别信息进行决策，给出目标识别身份的置信度。

基于PCR5理论的多传感器目标识别流程已经在图1中给出。可以看出PCR5理论作用于各个证据源产生的BBAs函数之间冲突量化估计、BBs函数之间冲突量化再分配及BBAs函数更新的全过程。图1最后得到的多传感器目标识别信息融合是经过PCR5处理的结果，已经包括了证据源产生的BBAs函数之间的内部冲突，使得即使多传感器产生高冲突信息也可以得到准确融合结果的目的。

图1 基于PCR5的非合作目标识别架构

3 仿真实验

为了验证基于PCR5理论的多传感器数据融合的有效性，本文分别给出了对于多传感器对于空中一个非合作目标识别的两个例子，分别为低冲突和高冲突两种情况。这样假设多传感器包括五种，分别为雷达(RDR)、红外(IRST)、电子侦察(ESM)、通信侦察(CSM)和光电(EO)，识别的目标为非合作的空中目标，识别框架Θ包括三种元素，分别为运输机(C)、战斗机(B)和民航飞机(P)。在仿真中，用到了Dempster合成规则、Yager合成规则、孙全合成规则、Murphy合成规则等规则[9, 10, 11, 12]，与PCR5合成规则进行比较。

实例1：对于低冲突BBAs情况，在某时刻各个传感器获得的基本信度指派如表1所示。

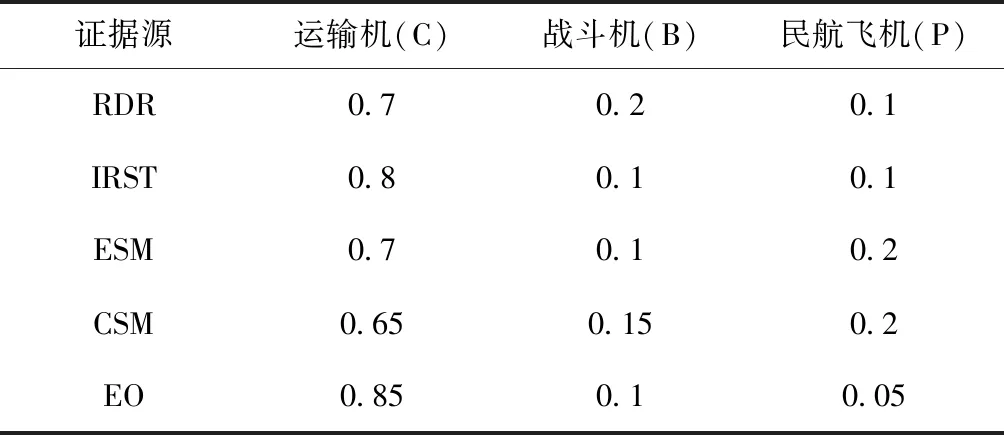
表1 冲突传感器基本信度指派

从表1中可以看出，五种传感器对目标的识别信息中，给运输机目标都分配了较大的BBA数值，而五种证据源BBAs函数冲突信息仅为0.2612，这种情况的BBAs函数可以看成是低冲突情景。

表2中给出多传感器信息融合后得到的BBAs函数。可以看出Dempster融合规则得到了对于运输机最高的置信度，达到了0.99978，对于其他两种目标类型给的置信度几乎为零。尽管后两种目标类型的确在表1中很小，但是融合结果过于弱化后两种结果对融合输出也不能说是完全有利的，因为较低置信度结果使得后两种目标类型作为不可能的存在。但是在表1中并没有反映出后两种类型是接近于0概率出现的，这种结果很可能会使得情报处理系统处于危险的环境而不能告警。而Yager融合规则和孙全规则得到的目标运输机类型置信度很小，已经不能反映出表1中所给的真实信息，这两种算法将很大一部分置信度都分配给了未知集合，造成多传感器目标置信度损失。Murphy融合规则与Dempster融合规则情况类似，都不能反映出后两种目标类型作为小概率事件出现的可能性。而PCR5融合规则的结果作为完美，与表1中给出的BBAs函数的最为贴合，即给出了运输机类型最大的置信度，同时也没有否认后两种类型出现的可能性，而后两种类型出现的置信度与表1中给出的BBAs函数大体相当。所以对于低冲突BBAs函数的融合PCR5是最佳选择之一。

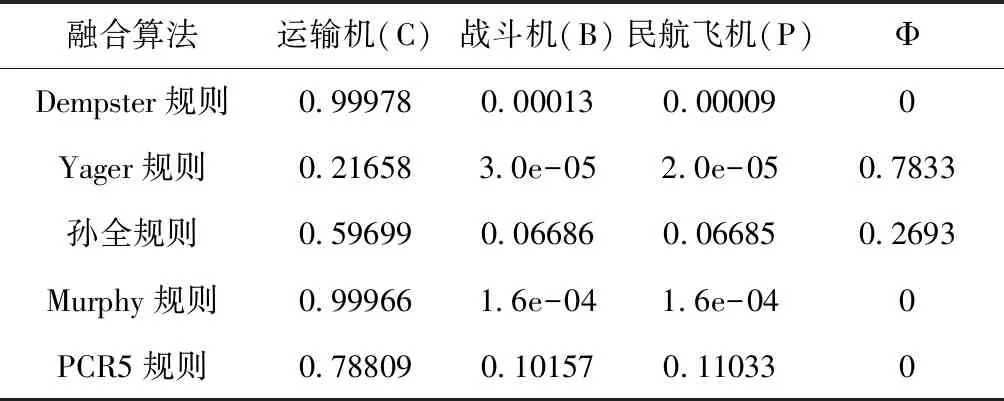
表2 低冲突多传感器信息融合结果

实例2：对于高冲突BBAs情况，在某时刻各个传感器获得的基本信度指派如表3所示。

表3 高冲突传感器基本信度指派

表3中给出的多传感器对于目标类型的BBAs函数式矛盾的，因为RDR和CSM认为目标是运输机，IRST和EO认为是战斗机，ESM认为是民航飞机，对于各种类型的判断，传感器之间都有矛盾，而且冲突信息较大。根据公式(8)，冲突信息为0.91，所以可以判断为高冲突场景。

表4给出了高冲突场景下多传感器信息融合后得到的BBAs函数。对于Dempster融合规则显然是失效的，因为已经不能对目标类型进行识别，冲突信息已经使得融合公式产生歧点。Yager融合规则此时也失去了判断能力，将BBAs函数完全分配给未知成分。孙全融合规则结果类似，三种类型分配的置信度相似，但是大部分也都分配给未知类型。Murphy融合规则给前两种类型分配了相近的大置信度BBAs，而给民航飞机非常小的置信度，这种分配方式放弃了ESM传感器给出的BBA，这种忽略ESM传感器识别结果是不可取的，而且ESM给出的BBA函数对于民航飞机还是非常高的，更加忽略民航飞机出现的可能性。而PCR5给出的三种目标类型置信度相近，同时民航飞机稍小于其他两种类型置信度，对于表3给出的BBAs函数是合理的。即反映出了ESM传感器给出的民航飞机高BBA，同时也反映出了其他四种传感器对于民航飞机类型给出的低置信度，是合理的，所以PCR5方法对于高冲突场景多传感器信息融合也是有效的，而且融合结果与识别前给出的BBAs函数实际意义比较接近。

表4 高冲突多传感器信息融合结果

实例3：在多传感器信息从低冲突场景过度到高冲突场景过程中，分析基于PCR5融合结果的变化情况。多传感器BBAs函数在表5中给出。

表5 多传感器BBAs函数

从表5中可以看出，在ε很小的情况下，场景冲突非常严重。而随着ε的增加，冲突成分越来越小，同时是呈非线性减小的，在这种情况下，考虑基于PCR5规则的融合后运输机BBA函数和战斗机BBA函数及两种并集BBA函数的变化情况，具体融合结果见图2所示。

图2 基于PCR5的多传感器信息融合

从图2中可以看到，融合后的运输机BBA函数随着ε的增加同样增加，而且也是近似抛物线曲线规律增加，同样战斗机BBA函数呈近似抛物线规律减小，而C ∩P的BBA函数不变。可以看出基于PCR5理论的融合结果同样能与融合前BBA保持相近的非线性变化，所以基于PCR5的融合方法对于场景冲突的非线性变化也是有效的。

4 结 语

本文给出了基于PCR5理论的多传感器目标识别方法，该方法不仅在低冲突场景下可以很好的对多传感器信息进行融合，同样对于高冲突场景下的多传感器信息也具有很好的融合效果。此外本文也对从低冲突到高冲突非线性变化的场景进行了PCR5融合分析，发现基于PCR5理论的融合方法对于这种冲突非线性变换的场景同样有效。