基于自适应中值滤波算法的研究与改进

赵玲玲

（重庆师范大学计算机与信息科学学院，重庆 401331）

0 引言

图像作为现代社会中一种不可或缺的信息来源，通过对图像进行加工处理获得图像包含的内容。但在通常情况下，各种噪声在图像生成或传输过程中使图像降质，使得后续对图像进行处理（如分割、压缩和图像理解等）时产生极大影响。因此，在使用图像的过程中，要对图像进行滤波处理。图像滤波是指在尽可能保留原始图像边缘和细节特征的情况下，对目标图像进行噪声抑制，用来减少不同脉冲噪声对图像的影响。噪声与图像的边缘和细节特征信号点之间可能存在某种相似性。当滤除噪声时，可能滤除边缘和细节信号点[1]。在实际的应用操作中，图像被过滤，但是边缘特征和图像的一些细节不能在过滤过程中一起过滤[2]。图像滤波分为线性滤波和非线性滤波。中值滤波是线性滤波中最典型的。其缺点是图像的边缘和细节容易模糊。非线性滤波，例如中值滤波，使用原始图像和模板之间的逻辑关系来获得结果。由于中值滤波被提出，它被广泛用于的图像噪声滤波[3-4]。

1 中值滤波算法

中值滤波使用技术为非线性平滑技术，该算法首先对图像的像素灰度值进行排序。图像中每个像素的灰度值被认为是当前遍历窗口中像素灰度值的中值，中值滤波的实现原理：图像像素灰度值中的一个点的值被该点的遍历窗口中每个点值的中值代替。这样做的目的是使其周围的像素值接近，从而消除非常大或非常小的噪声点[5]。该算法的总体实现是使用二维滑动模板。遍历模板的像素按像素值从大到小（或从小到大）排序。排序后的像素值产生二维数据的单调上升（或下降）序列[6]。二维中值滤波输出为：

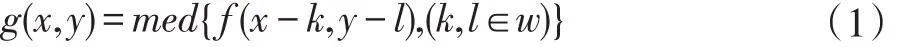
其中，f(x,y)是原始图像，g(x,y)是处理后图像。w表示滤波窗口（二维模板），一般有 3×3、5×5、7×7等模板。其实现过程为：

（1）选择合适的模板来遍历图像中的图像，直到模板的中心与图像中像素的位置一致；

（2）提取模板中各个灰度值对应位置的像素点灰度值；

（3）把提取到的灰度值按从小到大进行排列；

（4）确定排列的中值；

（5）用中间值替换模板中心位置上的像素灰度值。

2 自适应中值滤波算法

2.1 基本原理

自适应中值滤波算法选取一个m×n的矩形窗口sxy作为滤波窗口在图像上进行噪声检测。从而对图像的像素点作出噪声点与非噪声点的判断。执行过滤操作时，如果过滤窗口影响过滤操作，算法会根据预先设置的条件自动调整过滤窗口大小。否则，不要调整。输出过滤结果时，首先确定当前遍历窗口（即过滤窗口）中的像素的中值是否是噪声点。判断如果窗口中值是噪声点，则增大窗口。判断中值如果不是噪声点，则判断当前像素是否为噪声点。如果是，则用中值代替输出。如果不是，直接输出[7-8]。

2.2 基本步骤

自适应中值滤波算法分为两个进程，表示为进程A和进程B：

定义的变量：当前滤波窗口Sxy中的最小灰度值：Zmin。当前滤波窗口Sxy中的最大灰度值：Zmax。当前滤波窗口Sxy中的灰度值的中值：Zmed为。坐标（x，y）处的灰度值：Zxy。当前窗口Sxy允许的最大尺寸：Smax。

在图像噪声密度较小的情况下，中值滤波算法和自适应中值滤波算法都表现出了较好的去噪性能。如在噪声密度为0.2的情况下，中值滤波和自适应中值滤波算法滤波性良好，并且对图像的边缘和细节有较好的保持。但是，当噪声密度大于或等于1/2时，中值滤波算法和自适应中值滤波算法的滤波性能逐渐下降，如在噪声密度为0.5时，中值滤波后的图像有雪花状噪声，噪声密度为0.8时，雪花状噪声出现更多，而自适应中值滤波后的图像也出现雪花状噪声，图像的边缘和细节保持性能较噪声密度为0.2时下降，如图1所示。

图1 两种算法对图像Lena的滤波效果比较

在对自适应中值滤波的改进中，如赵高长等人[9]在噪声检测时，对图像增加阈值处理，并在滤波时引入均值滤波的思想，并用加权的方法得出中值然后输出。但是在这一改进中存在以下问题：①阈值的大小难以确定，需要多次的实验来确定，加大工作量；②采用均值滤波，进行加权，带入了线性滤波的缺点即模糊了图像的边缘与细节，而这种现象与最初进行图像滤波的目的不同。张旭明等人[10]提议根据噪声干扰程度自动调整滤波器窗口大小。噪声被去除的同时，图像边缘和细节特征保持不变，但是判断噪声干扰程度的方法不容易确定[11-12]。针对目前中值滤波和自适应中值滤波算法中存在的这些问题，本文对标准自适应中值滤波算法做了一些改进，从而避免了这些问题。

3 基于自适应中值滤波的改进算法

标准的自适应中值滤波算法先判断滤波窗口的中值是否为噪声点，再判断当前图像像素点是否为噪声点。本文改进的算法先判断当前图像像素点是否为噪声点，再根据需要判断滤波窗口中值是否为噪声点。第一步噪声检测：先检测判断图像中该点的像素灰度值是否为噪声点。第二步滤除噪声。滤除噪声时对该像素点考虑多种情况。情况一，该像素点不是噪声点，直接输出该像素灰度值。情况二，该点是噪声点。检测此时滤波窗口中的中值（Zmed）是否为噪声点。在判断中值是否为噪声点时也要考虑多种情况。情况一，Zmed不是噪声点，输出此滤波窗口中值Zmed。情况二，Zmed是噪声，根据算法中已设定的条件自动增大滤波窗口尺寸，一直循环到选出正确的中值。但是，这样的循环操作中也会出现一些比较极端的情况，如，当滤波窗口自动增大到允许的最大窗口尺寸时，Zmed取值依然没有选出来，对当前滤波窗口做处理。除去窗口中的极小和极大灰度值，用剩余像素的灰度均值代替当前像素值输出。

改进算法的具体步骤：

定义变量：中心在（x,y）处的当前滤波窗口：Sxy。初始窗口大小：S0。允许的最大窗口大小：Smax。图像（x,y）处的灰度值：Zxy。Sxy中的极小灰度值：Zmin。Sxy中的极大灰度值：Zmax。Sxy中的灰度值的中值：Zmed。窗口均指当前使用的滤波窗口大小。

①如果 Zmin〈Zxy〈Zmax，输出 Zxy,否则执行②；

② 如 果Zmin〈Zmed〈Zmax，输 出Zmed,否 则 执行③；

③如果 Sxy+2≤Smax，增大窗口：Sxy=Sxy+2,执行①,否则转④；

④输出当前窗口中除去极大、极小灰度值的其余像素的灰度均值Savg。

算法改进的两方面：

（1）算法先判断当前像素是否为噪声，若不是则直接输出当前像素；若是噪声再判断当前窗口的中值是否为噪声，然后根据中值的判断结果执行是否增大窗口，算法逻辑清晰，降低算法复杂度。

（2）在图像噪声密度较小时，中值滤波和标准自适应中值滤波算法表现了较好的滤波性能。但在图像噪声密度较大的情况下，标准的自适应中值滤波算法判断当前像素和中值都为噪声。依然用中值代替当前像素值作为输出。这是不合常理的。而改进的自适应中值滤波算法解决了这了这一问题。

4 实验分析

利用MATLAB R2016a实验环境，依据本文提出的改进算法，进行仿真实验。通过对添加了不同密度的脉冲噪声的256×256图像Lena进行滤波，与中值滤波、标准自适应中值滤波结果进行比较来证明改进算法的有效性。数据分析时引入峰值信噪比（PSNR）作为客观数据的评价标注。

PSNR定义为：

其中m×n为图像大小；MSE是原图像与处理图像之间均方误差；I(i,j)为原始参图像；K(i,j)为加噪滤波后的图像。仿真实验效果如图2所示。

图2 三种算法对图像Lena的滤波效果比较

经过图2的三种算法的图像滤波效果比较：图像脉冲噪声密度为0.2时，三种算法的滤波效果基本没有差别；图像噪声密度为0.5时，中值滤波效果图出现较多的噪声点，影响较大，而标准自适应和改进的自适应中值滤波表现较好，基本没差别；当图像噪声密度变大为0.8时，三种算法出现明显差别，中值滤波噪声点影响最大，标准自适应中值滤波出现雪花状噪声点，与前两种算法比，改进的算法滤波效果更好。不同算法的效果性能如图3所示。

图3 三种算法的滤波性能比较

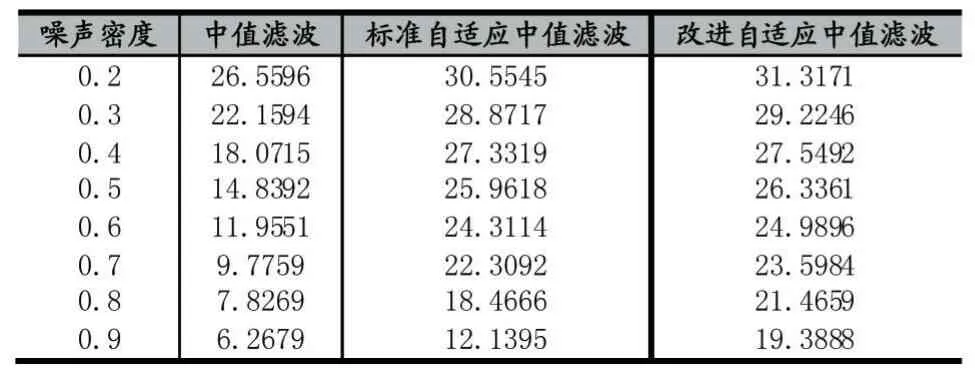
表1 三种算法对标准图像Lena滤波PSNR比较（单位：dB）

三种滤波算法对不同密度脉冲噪声的PSNR如图3所示，与图2相对应的不同噪声密度的PSNR值如表1所示。从图3可得，在不同噪声密度下，中值滤波滤波效果整体较差；而自适应中值滤波和本文的滤波算法在噪声密度较小时，滤波效果接近，改进的算法PSNR稍大一点，差别不大，如噪声密度为0.2～0.4。当噪声密度增大时，自适应的两种算法PSNR差别明显变大，改进的自适应算法PSNR明显大于标准的，如噪声密度：0.6～0.9，并且从图3中各算法的PSNR的图形得出随着噪声密度的变大，两种自适应算法的PSNR的差距呈逐渐增大趋势。

5 结语

与中值滤波算法相比，标准的自适应中值滤波在保持图像的边缘和细节的同时，可以有效地滤除图像的不同密度的脉冲噪声。但中值和标准自适应滤波算法始终存在局限性。针对这些局限性，本文提出了对自适应中值滤波的改进算法，并通过仿真实验以及其数据分析证明，提出的改进自适应中值滤波算法的滤波性能优于中值滤波和标准自适应滤波。