非正常航班成本分析及优化

李琳丹，许雅玺

（中国民用航空飞行学院机场工程与运输管理学院，广汉 618300）

0 引言

社会进步，经济发展，航空出行已成为当代人首选的出行方式，不断增长的航班量带来航班正常率的持续下降。据FlightStats网站统计，2017年2月我国Air China（国航）准点率为 66.55%，China Eastern（东航）为61.74%，美国本土的平均航班准点率也只有77%。恶劣天气、机场保障、航空公司等都是造成航班延误或取消的重要原因，给出行旅客带来极大不方便的同时机场、航空公司也承受了巨大损失。同时需要注意的是，国内航空公司在主要航线上的航班安排已经十分紧密，一旦某个航班受到影响，其延误波动将在航班网络中产生多米诺效应，引起更大面积航班瘫痪[7]。及时有效的恢复航班，保证航空公司恢复成本最小，单纯依靠调度员手工恢复是不可行的。但基于计算机技术的最优化算法可快速达到目标，在降低延误损失的同时提高签派员工作效率，为后续机组排班以及航空公司其他研究提供依据[1,2]。世界各国民航组织、航空公司逐渐重视航班恢复问题，中国也将航班恢复紧急提上议程。

国内外学术界研究航班恢复问题已有较长时间，也取得了一定的成果，何昕等人的枢纽机场航班延误恢复模型研究，在航空和高速铁路联合运输的思想上延伸，建立枢纽机场大面积航班延误恢复模型，利用高速铁路替代模式降低延误成本[3]。田倩南等人的受扰航班恢复问题的优化方案研究，提出一种改进的时空网络算法，利用占优准则减少可恢复航线的组合数量，借助CPLEX软件实现延误成本的降低[4]。JARRAH等人研究了飞机资源短缺的问题，针对航班延误和航班取消的情况，建立最小费用流模型求解[5]。赵秀丽等人的不正常航班延误调度模型及算法，构建了以延误成本最小或延误时间最短为目标的航班恢复模型，采用启发式方法和匈牙利算法对模型求解[6]。上官栋栋等人的应用遗传算法求解航班恢复问题，根据面向对象的编程思想设计了航班调度算法并耦合遗传算法对旅客滞留航班恢复模型进行求解，针对大规模航班有一定优势[7]。前人研究大多集中在理论模型的研究，在实际运用中很难快速解决问题，针对签派员调度实操适用性不强。

1 非正常航班问题描述

非正常航班又称不正常航班，其包含恶劣天气、飞机机械故障、空中管制等原因造成的航班计划非正常执行。不正常航班涉及的因素较多，实际情况十分复杂，是一个大规模优化问题。本文主要研究因持续恶劣天气航班延误短时间无法恢复或机械故障无法当天修复，航空公司没有可调度的空闲飞机执行原飞行计划，因此只能利用后续可用航班、新开航班等重新制定72小时航班调配方案。运用优化理论知识，合理利用运力资源，以运行成本最低为目标将航班延误的旅客及货物安全运输到目的地。

航班恢复问题的“难”除涉及因素多且杂以外，更重要的原因是需要达到恢复的及时性，等待的每一分都会增加各方损失。在手工调整情况下，调度员只能考虑到影响安全的相关因素，很难考虑到延误成本的问题。解决该问题的关键在于如何建立适用的优化模型，如何借助合理的工具快速实现。当前业界提供解决航班恢复问题的产品只有Sabre一家。基于此本研究从延误成本角度建立规划模型，提出解决航班延误的合理方案，并借助计算机软件快速实现，最后基于实例对模型算法进行验证。

2 航班延误恢复模型构建

2.1 模型假设

非正常航班优化问题涉及的变量较多，难度较大，为了增强模型的可操作性，简化数学模型，突出延误成本优化特点，本研究将做如下假设：

（1）假设放弃行程及退票旅客都视为改签；

（2）各舱位旅客无随身携带行李，从高到低托运行李依次为40kg,30kg,20kg；

（3）各舱位旅客不挑剔重新分配舱位；

（4）货物质量均为整数。

2.2 模型符号

本研究中模型符号的含义如表1，其中i=1,2,3表示头等舱、商务舱、经济舱；j=1,2,...,h表示可用航班个数；W0i=0表示不新开航班，W0i=1表示新开航班。

2.3 函数构建

非正常航班优化目标函数为延误总成本最小，借助数学规划的思想，引入0-1变量W01、W02、W03，表示是否新开航班及新开航班的飞机类型。表示可用航班各舱位旅客延误成本之和，表示新开航班各舱位旅客延误成本之和，表示可用航班货物延误成本总额，gnyn表示新开航班上货物的延误总额，表示延误旅客退票及改签成本总额。综上目标函数为：

约束条件：

表1 模型符号及含义

其中约束条件表达式1表示可用航班安排旅客人数应小于该航班各舱位的最大剩余座位数；函数2表示新开航班旅客安排数量不多于该航班总座位数；函数3表示可用航班、新开航班分配人数与退票改签人数的之和为旅客总延误数；函数4表示利用可用航班运输延误货物质量小于该航班剩余载重量；函数5为新开航班可运输的货物质量，函数6为总的延误货物量；函数7、8表示是否新开航班，新开航班是大型、中型或小型飞机。

3 算例分析

3.1 算例数据

受持续恶劣天气侵扰，某年8月上午7：40由成都飞往上海的某次航班发生延误且短时间无法恢复，遂该航班被迫取消，此次延误造成了318名旅客和3560公斤货物发生延误。签派员立即查询72小时内可用的航班时刻为 12：30、15：50、17：20和次日凌晨 6：20。

可用航班：

12：30各舱位延误成本分别为120元/人、84元/人、60元/人（默认顺序：头等舱-商务舱-经济舱），货物延误成本为3元/kg，最大允许人数为36人，最大允许重量为2160kg；

15：50各舱位延误成本分别为132元/人、86元/人、62元/人，货物延误成本为3元/kg，最大允许人数为28人，最大允许重量为2380kg；

17：20各舱位延误成本分别为148元/人、92元/人、66元/人，货物延误成本为3元/kg，最大允许人数为18人，最大允许重量为2108kg；

次日6：20各舱位延误成本分别为220元/人、188元/人、168元/人，货物延误成本为3元/kg，最大允许人数为46人，最大允许重量为1980kg。

新开航班：

大型飞机，固定成本140000元，各舱位延误成本分别为130元/人、90元/人、65元/人，货物延误成本为2元/kg，最大允许人数为360人，最大允许重量为13000kg；

中型飞机，固定成本90000元，各舱位延误成本分别为130元/人、90元/人、65元/人，货物延误成本为2元/kg，最大允许人数为 234人，最大允许重量为10000kg；

小型飞机，固定成本48000元，各舱位延误成本分别为130元/人、90元/人、65元/人，货物延误成本为2元/kg，最大允许人数100人，最大允许重量为9000kg；

此外，本次延误中4名头等舱、5名商务舱和18名经济舱旅客已改签至其它航班,其带来的改签成本分别为 68元/人、46元/人、32元/人。

该算例结合上述数据利用72小时可用航班及新开航班运输延误旅客及货物,求得最小延误总成本及分配方案。各航班各舱位最大允许旅客人数如表2所示。

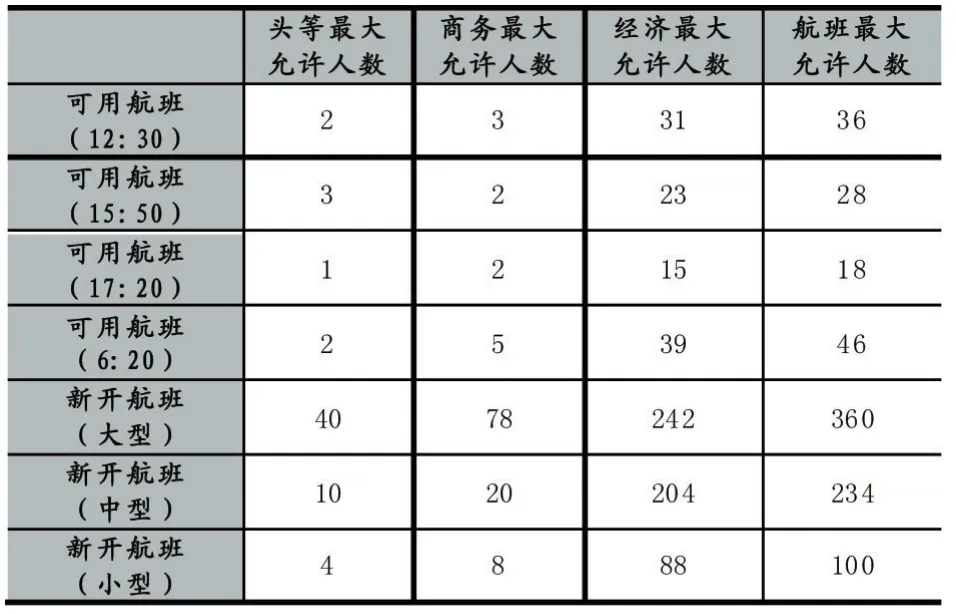
表2 各航班舱位最大允许旅客人数

3.2 具体步骤

模型相关步骤：

（1）采集航班延误旅客人数、货物数量及相关成本数据等；

（2）完成数据整理工作；

（3）根据上述公式（1）～（9）构建模型；

（4）编辑程序语言，输入LINGO软件；

（5）得到延误成本，验证结果是否符合实际要求，符合输出，反之检查问题，重复上述步骤。

3.3 实验结果分析

算例结果如表3所示，新开航班为中型航班，新开航班运输旅客217人，3560kg货物全部由新开航班运输完毕；可用航班 12：30/15：50/17：20/6：20 头等舱分配旅客为 0人/0人/0人/0人；可用航班 12：30/15：50/17：20/6：20商务舱分配旅客为3人/2人/0人/0人；可用航班 12：30/15：50/17：20/6：20 经济舱分配旅客为 31人/23人/15人/0人，该航班最小延误成本为113768元。

表3 实验结果

4 结语

本文在充分考虑航班恢复的实际背景后，从航班延误成本角度出发，利用可用航班，新开航班等方式，建立适宜数学规划模型，基于计算机LINGO软件编程快速实现低成本签派运输延误旅客及货物，最大程度降低航空公司、机场、旅客的损失[3]。本文建立模型及算法具有普适性，能够在较短的时间内计算出最低的延误成本方案并制定出相应航班恢复计划，模型较为合理，算法有一定的科学性，能为签派员提供便利，具有一定的研究价值和发展潜力[3]。模型仅从延误成本角度考虑航班安排，未考虑到航班延误时间及舱位匹配问题，与实际存在差距，这也是需要进一步研究改进的地方。