热声载荷作用下薄壁结构非线性响应分析和试验验证

沙云东，张墨涵，赵奉同,2,*，朱付磊

1. 沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136 2. 北京航空航天大学 能源与动力工程学院，北京 100083

热声载荷作用下结构动力学响应特性及疲劳预测是现代高速飞行器结构设计和安全性的重要因素。火焰筒壁板、发动机机匣、涡轮叶片和飞行器蒙皮等都会受到高温及声压的影响。飞行器热保护系统(TPS)表面温度可达1 600 ℃以上，声压级(SPL)可达180 dB[1]。TPS在高声压级下会产生较大位移，并可能在高温下出现屈曲。为提高航空飞行器的飞行性能即解决严重的气动、声学和热环境下的疲劳问题，应统计大量薄壁结构呈现出的非线性响应[2-6]，并进行疲劳寿命的预测[7-9]。因此，为了满足航空薄壁结构的结构设计要求、降低研究成本，有效的热声动态响应分析成为当前的重要任务。

薄壁结构仿真对提高试验的有效性和可靠性起重要作用。结构非线性响应模拟分析方法主要有：摄动法、 Fokker-Plank-Kolmogorov(FPK)方程、von Karman-Herrmann大挠度板方程、蒙特卡罗法、等价线性化(EL)方法、降阶模型法(ROM)和有限元数值积分方法(FEM)。已证明摄动法[10]仅限于较弱的几何非线性，而FPK方程仅对单自由度(DOF)系统有精确解。蒙特卡罗模拟[11-12]是最常用的方法，但偏微分方程和伽辽金法(Galerkin)仅适用于较简单的结构[13-14]。等价线性化方法已被广泛应用，因为该法能够准确获取大范围的响应统计，同时保持较轻的计算负担[15]。其缺点是假设的响应必须是高斯分布。对于有限元数值积分方法[16]，计算成本是主要关注的因素。有限元模型通常包含数百个物理自由度，且非线性项在每个时间步都会更新及重新组合。Dhainaut等[17]提出了一个用于预测受热声载荷作用下薄板的非线性随机响应的有限元公式。为了验证公式，模拟的数值结果包括最大位移和应变的均方根值、位移和应变响应的时间历程、概率分布函数及功率谱密度等。杨智春等[18]通过分析壁板跳变运动产生的机理定义了“穿零频次”，将跳变运动定量进行分类，得出了在颤振临界动压前，动压的增大会导致薄壁板势能阱深度呈现先增大后减小趋势的结论。杨雄伟等[19]使用混合有限元-统计能量方法分析了高温环境、165 dB声压作用下的结构声振特性，总结了热应力对结构模态频率的影响规律，以及材料物性对模态频率与振动响应的作用。桂业伟等[20]从单向及双向耦合两方面研究了流-热-固多场耦合问题，对国内研发的热响应耦合分析平台进行总结并讨论了未来的发展趋势。文献[17-20]均以理论公式及仿真计算为主体，并未有试验验证作为支撑。Liu等[21]通过对比试验测得的后屈曲偏转与有限元模拟后屈曲分析得到的结果，由一阶模态方程推导出了动态响应参数的变化，从而描述了从线性振动到完全非线性动态响应的转变，得出了声激励、热应力和结构刚度的组合对动态响应的影响。刘磊等[22]结合热-流-固耦合试验需求开展了风洞试验，通过计算对比分析验证了多场耦合计算平台方法的有效性，并预估了高温合金模型的试验结果。侯薇等[23]建立了基于截面平均的准一维非线性热声模型，并进行数值求解，采用宽频时域声阻抗边界条件，预测了临界起振温度及热声系统的瞬态压力波。以上文献[21-23]均为在同一模型上进行了仿真与试验的对比及预测，而本文是在仿真与试验对比的基础上做了适当的拓展仿真，即在薄壁板的基础上做了加筋薄板的仿真。

基于文献[24]，本文首先采用了一种新型航空发动机材料GH188，对热环境下薄壁方板进行声激振试验，得到了加速度响应和应变响应的结果。然后，根据冯卡门大挠度理论，采用耦合的FEM/ROM方法对薄壁板的动力学响应进行计算。再将热声试验测得的响应结果与数值仿真结果进行对比，验证了热声仿真计算分析方法的精度与有效性。最后，利用该计算模型计算了在不同温度场及声载荷作用下四边固支交叉加筋金属板的动力学响应，并进行了详细的对比与分析。

1 非线性响应理论

1.1 平板结构有限元控制方程

根据有限元法对各单元振动方程进行推导和求解运算，得到整体结构控制方程：

(1)

式中：M为质量矩阵；K为刚度矩阵；W为整体位移；FT为合外力。

设时间步长为eiωt，i为步数，ω为频率，t为时间，则结构振动方程可记为

(2)

式中：Φn为结构法向振型；ωn为结构基频，分析阻尼对结构响应特性的影响，将有限元与边界元方法进行耦合分析，得到结构在模态坐标下的运动方程为

(3)

其中：dn为模态位移；ζn与Mn分别为阻尼系数和模态质量。对结构模态坐标运动方程式(3)进行推导，可以获得响应函数表达式为

(4)

将式(3)与式(4)结合，则式(4)转化为

HSd=ΦΤFT

(5)

式中：HS为响应函数；d为模态位移；Φ为模态矩阵。

将模态载荷FT分解为外力载荷Fe和声压载荷FP两部分，控制方程变为

HSd=ΦΤFP+ΦΤFe

(6)

式中：ΦΤFP为声压向量，从边界元系统传递到到有限元中，传递过程如图1所示。

通过式(6)，得到平板结构控制方程为

HSd=(LT)ΤFP+ΦΤFe

(7)

式中：LT为传递矩阵。

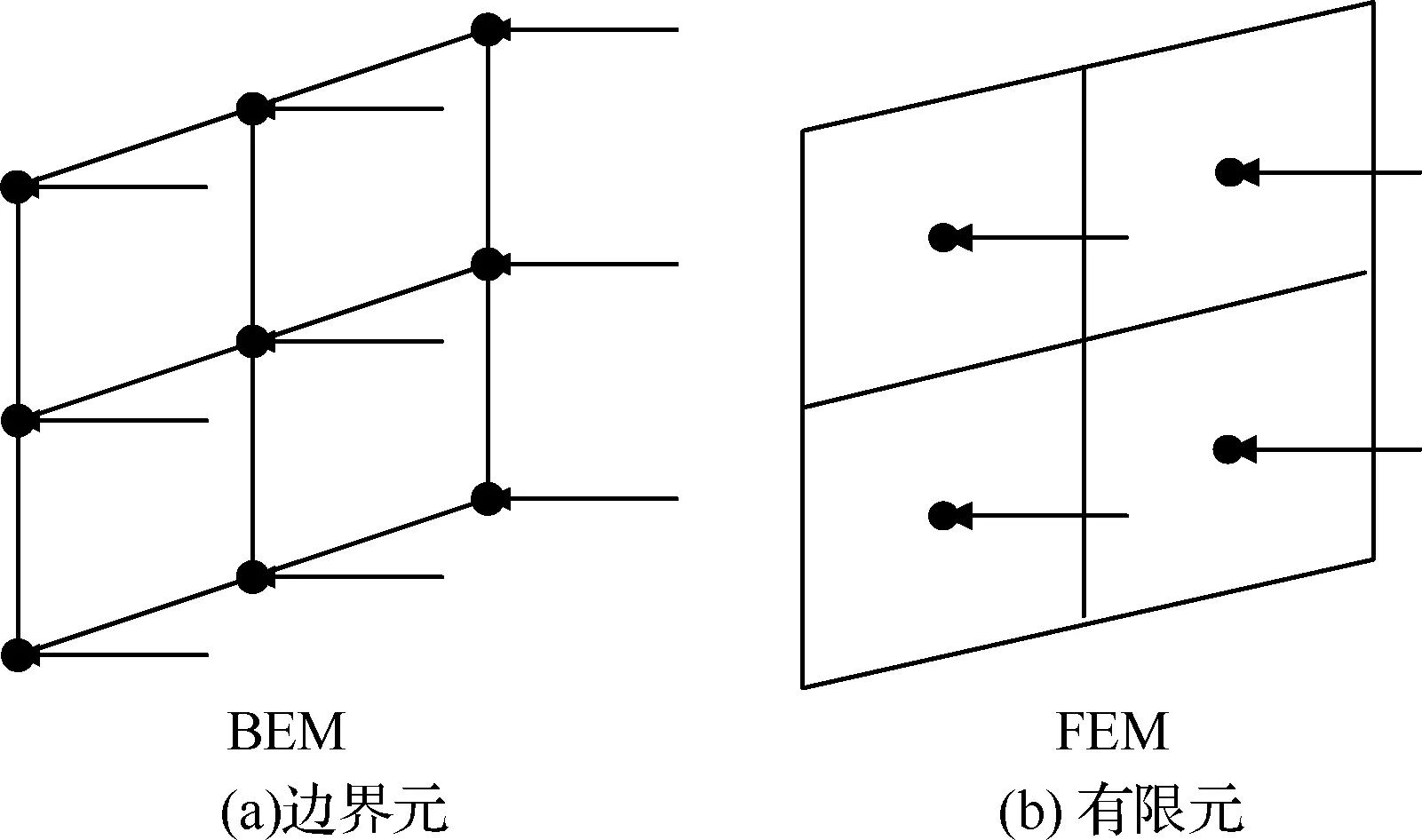
图1 有限元与边界元传递过程Fig.1 Transfer process of finite element and boundary element

1.2 薄壁构件大挠度方程

薄壁构件在热声载荷作用下大挠度方程的推导是在克希霍夫积分方程和冯卡门大挠度方程2个 理论假设的基础上进行的。以薄壁结构中截面位置为参考，推导结构上任意位置处各方向应变的表达式为

(8)

针对结构应变和位移响应进行矢量微分计算，得到带有挠度项的变形协调方程：

(9)

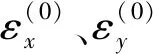
将艾里应力函数F引入，式(8)可表示为式(10) 的形式

(10)

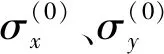
将式(9)与式(10)联立，可以转化成式(11)中带有应力函数项的变形协调方程：

(11)

(12)

式中：ρ为密度；ξ为阻尼系数；υ为泊松比；p(x,y,t)为模拟声载荷的随机应力；D为弯曲刚度；θ为板厚的温度梯度。

1.3 薄壁构件热屈曲理论

随着温度的逐渐升高，薄壁结构因受热而产生的压应力会引起热屈曲，导致结构变形并丧失承载能力，此时的温度定义为临界屈曲温度，用T*表示。四边固支板的一阶临界屈曲温度表示为

(13)

式中：β=b/a为薄壁构件宽与长之比。将温度无量纲化，表示为：T0=T0/T*，T0为高出常温的那部分温度，故

T=T0+δvT0fv(x,y)+δgT0fg(x,y)

(14)

式中：T为任意一点温度；δvT0和δgT0分别为整个板面上温度变化值的幅值大小和沿板厚度变化的温度的幅值；fv(x,y)和fg(x,y)分别为薄板面上温度变化情况和任一点(x,y)处温度变化情况。

2 薄壁板热声载荷试验验证

2.1 薄壁板热声试验

该试验是针对GH188板材开展高温环境下声激振的动力学响应试验。试验件的几何尺寸与应变片的贴片位置如图2所示，其中板厚1.5 mm。1# 与3#应变片在薄壁板的短边中点，以测量试验件x方向的应变；2#与4#应变片在薄壁板的长边中点，以测量试验件y方向的应变。不同温度下的材料参数如表1所示,K为热导率。通过口框夹具将试验件压紧，并采用双排螺栓拧紧的方式对试验件四周固定，以实现四边固支约束。采用双面加温的方式对试验件进行加热如图3所示，温度载荷为50～250 ℃，间隔为50 ℃；采用声场控制方法施加有限带宽高斯白噪声，频率范围为100～1 250 Hz，加载的总声压级范围为142～154 dB，间隔为3 dB。

本次试验有2个目的，一是对变形高温合金材料随机疲劳性能测试试验系统开展联合调试，验证系统的有效性；二是在给定的不同温度及声载荷条件下获取变形高温合金材料结构表面指定位置处高温声激振测试的动态应变响应。

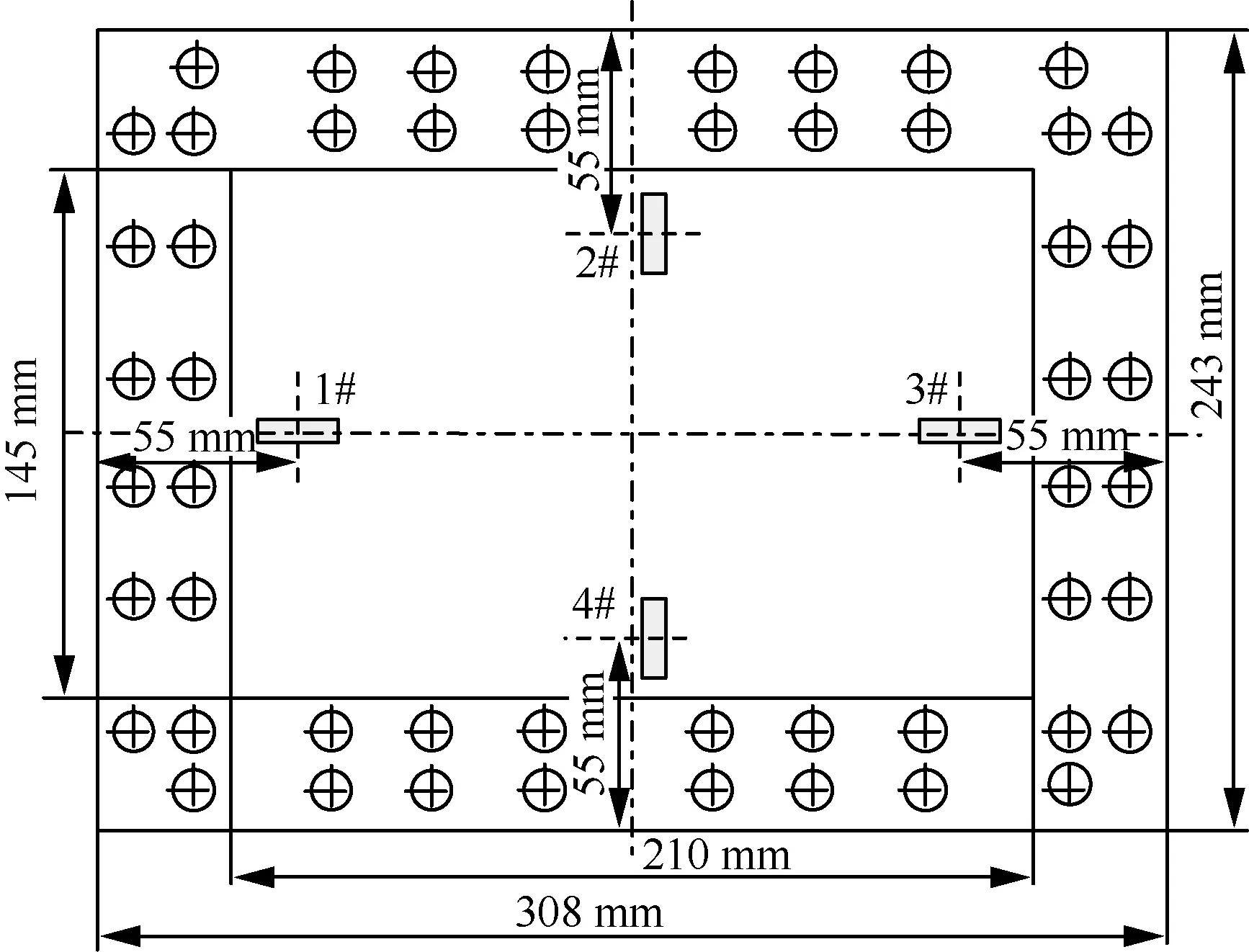
图2 试验件尺寸及应变片位置Fig.2 Sizes of test piece and locations of strain gage

表1 GH188材料参数Table 1 Material parameters of GH188

ParameterT=50 ℃T=400 ℃T=600 ℃E/GPa208175156υ0.3010.3180.326α/(10-6 ℃-1)11.713.414.4ρ/(103kg·m-3)9.099.099.09K/(W·℃-1)15.719.627.1

图3 试验件加热现场照片Fig.3 Photo of test piece heated on site

试验结果表明，试验系统能满足试验要求，且能实现噪声载荷和热载荷的联合加载，并能给出有效测试结果。在给定的频带范围内声压级可达157 dB，试验件表面温度可达500 ℃。同时也分析总结出了结构动态响应特征以及随温度和声载荷变化规律。得出了结构屈曲前和屈曲后过程响应数据，为进行仿真对比验证提供了有效数据。

2.2 仿真对比验证

为了确保仿真的准确性，仿真对象的特性、边界条件和热声载荷等均与试验相同。同时采用FEM/ROM方法计算薄壁板的热声动力学响应，并提取与试验相同位置的应变响应,进行仿真与试验的对比验证。

在试验过程中，利用激光测振仪获得了不同热声载荷组合作用下薄壁板中心位置的加速度响应，如图4所示。通过对不同温度下薄壁板的一阶模态频率分析可以得出加速度响应和应变响应。本项试验对象为GH188板材样件，选用BAB350-5AA250(11)-150型中温应变计，该应变计为自补偿应变计，可自动修正热输出，无需在结果上再进行修正。表2为不同温度下结构基频试验结果，由于高阶响应幅值远低于基频响应，所以只给出了试验基频。表3列出了仿真的前六阶模态频率，可以看出，100 ℃为薄壁板的临界屈曲温度。对比结果表明两者的一阶模态频率具有一致性，均呈现出先降低后升高的趋势。对于薄壁板在前屈曲区域保持软化，并在后屈曲区域转化为硬化得到了验证。图5表示试验测试的声压级为151 dB时，在1#测点的代表性加速度响应谱，在前屈曲区域T=50 ℃时，一阶模态频率为347 Hz，而在后屈曲区域T=150 ℃时，一阶模态频率为306 Hz。图6为薄壁板在SPL=151 dB时T=50,100,150,200 ℃的应力响应云图，可看出各温度下薄壁板的危险点位置，反映了结构整体响应特性。

图4 试验中的加速度测量Fig.4 Acceleration measurement in test

声压级为145 dB和151 dB时，应变片测量了与试验件长边和短边中点的基频对应的应变响应值，表4所列的是试验与仿真的长边中点和短边中点应变响应值。结果表明，仿真应变响应值与试验结果非常吻合，验证了薄壁板在热声载荷作用下的非线性动力学响应模型和计算方法的有效性。图7给出了试验测试的短边中点(1#)声压级为151 dB时，温度载荷为50 ℃与150 ℃这2组 代表性应变响应谱，屈曲前T=50 ℃时，应变响应值为10.7×10-6，屈曲后T=150 ℃时，应变响应值为16.6×10-6。

表2 不同温度下结构基频试验结果

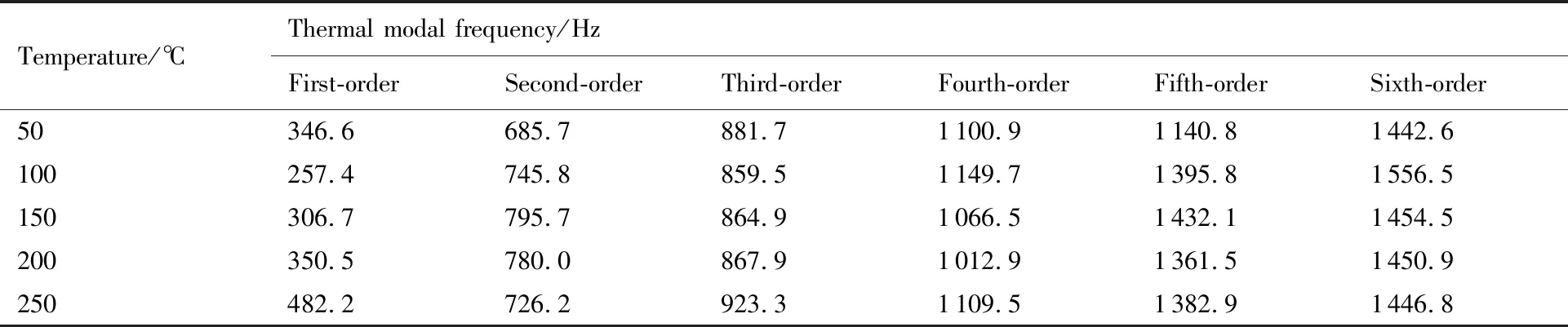
表3 不同温度下结构前六阶热模态频率计算结果Table 3 Calculation results of the first six thermal modal frequencies of structures at different temperatures

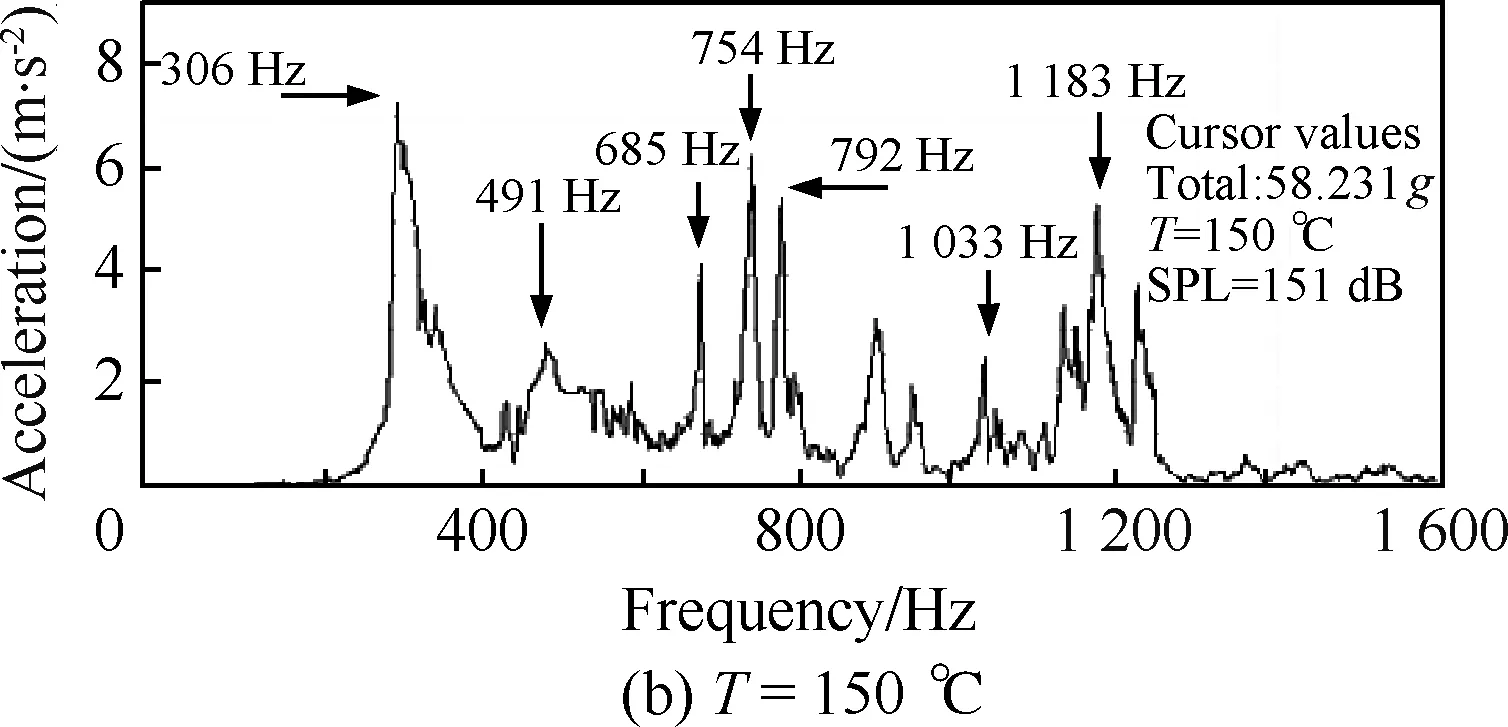
图5 薄壁板中点的加速度响应Fig.5 Acceleration response on thin-walled panel midpoints

图6 薄壁板应力响应云图Fig.6 Stress response contours of thin-walled panel

综上所述，通过本次对高温合金薄壁板进行高温环境声激振试验和数值仿真，分别对比了一阶模态频率和测点的应变响应值，充分验证了热声载荷作用下薄壁板非线性动力学响应模型和计算方法的有效性。

表4 测点位置单元在基频处的单向应变Table 4 One-dimensional strain at fundamental frequency of measuring point unit

图7 试验件应变频域响应Fig.7 Frequency-domain response of test piece

3 热声载荷条件下非线性响应分析

数值仿真计算对象选择图8所示的四边固支交叉加筋板，其性能与试验的薄壁板保持一致，表5 列出了特定的几何参数，其中h1为肋宽，h2为肋高。假设热载荷均匀分布在板的表面，声载荷是有限带宽高斯白噪声，带宽频率范围为0～2 000 Hz。本文主要提取模型中间节点处的热声响应结果以分析其振动特性，如图8所示。图9为结构的有限元网格划分。

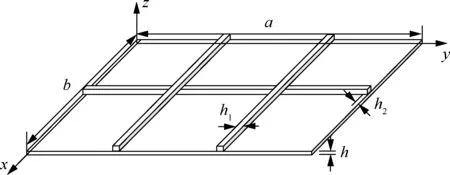
图8 交叉加筋板示意图Fig.8 Cross stiffen-reinforced plate sketch

表5 几何参数Table 5 Geometric parameters

Parametera/mmb/mmh/mmh1/ mmh2/ mmValue2101451.51.51.5

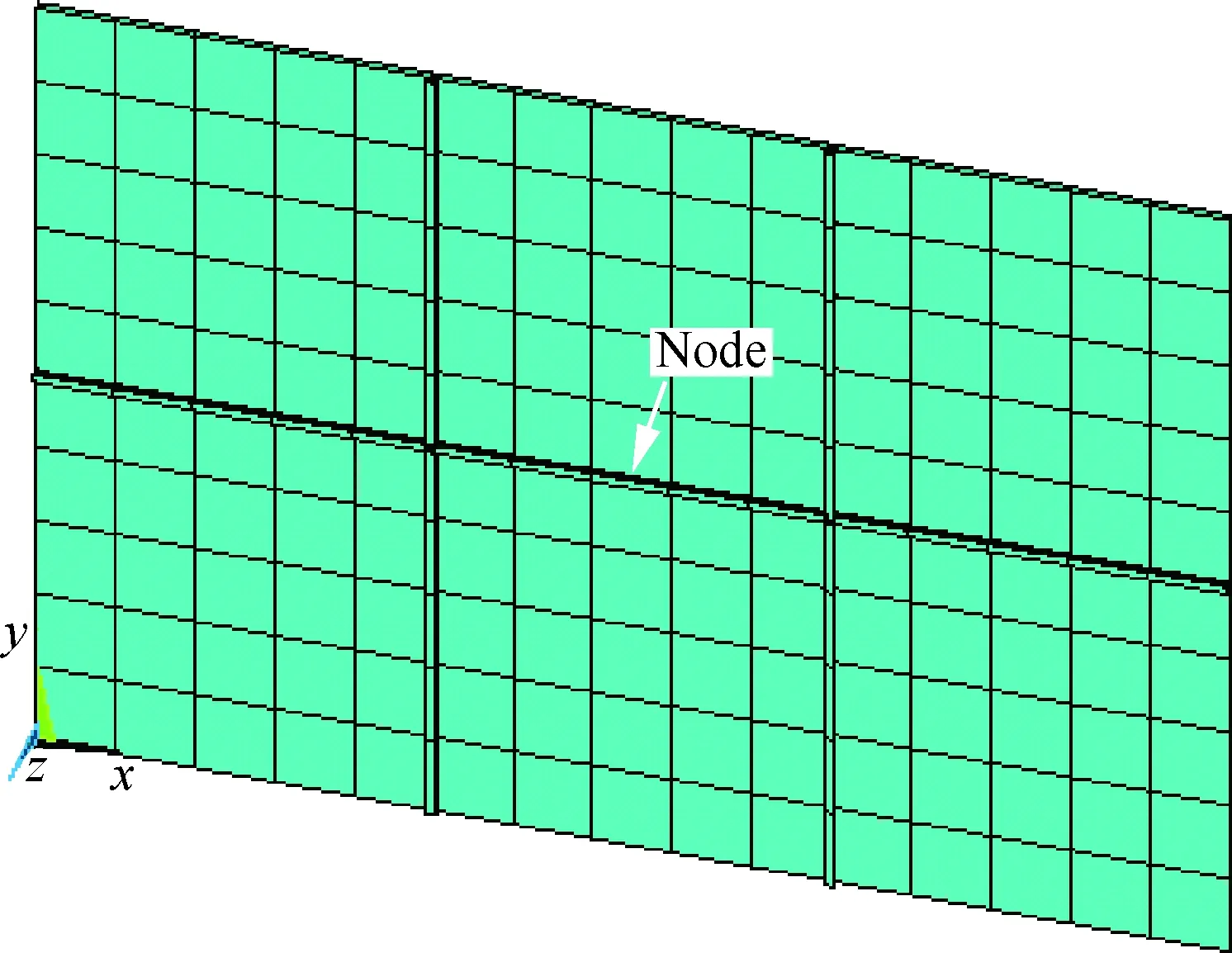
图9 加筋板的有限元网格模型Fig.9 Finite element mesh model of cross reinforced plate

采用有限元法计算出加筋薄壁板的第1阶临界屈曲温度Tcr=27.5 ℃。为便于表达，本文均以热屈曲系数S来表示温度，其中S=T/Tcr，T为实际温度。以热屈曲系数S的大小为标准，有3种典型状态，S<1、S=1和S>1分别代表屈曲前、临界屈曲和屈曲后状态。常温状态下(20 ℃)加筋板的前六阶模态频率如表6所示。本文在不同S与SPL组合作用下获得了加筋板的动力学响应，其中S为0～20，间隔为0.1，SPL的范围为145～172 dB，间隔为3 dB。

表6常温环境下加筋板前六阶模态频率

Table6Firstsixordermodalfrequenciesofstiffen-reinforcedplateinnormaltemperatureenvironment

Order123456Frequency/Hz490.36778.591273.61310.51509.81886.3

3.1 横向位移响应分析

室温条件下(S=0.2)，加筋板围绕初始平衡位置做随机振动，随着声压级由160 dB升高到172 dB， 振动响应加剧，位移响应幅值由0.5 mm增大到2.1 mm，如图10(a)、(d)所示。当温度升高到S=0.6时，位移响应幅值随之增大,由0.5 mm增大到1.0 mm和由2.1 mm增大到2.3 mm，如图10(b)、 (e)所示。当温度达到临界热屈曲温度S=1.0 时，位移响应幅值明显增大，由1.0 mm增大到1.3 mm和由2.3 mm增大到2.6 mm，如图10(c)、 (f)所示。图10中清晰地显示了屈曲前，随着温度的升高，位移时间历程越来越稀疏；且固定条件下，位移响应与振动响应基本相同，不同振动方向的幅值基本一致。

图11为加筋板在声压级为172 dB条件下屈曲后的横向时间位移响应，其位移响应的运动趋势取决于热载荷与声载荷的相对强度。当加载温度稍高于临界屈曲温度时，声载荷强度高于热载荷强度，声载荷足以克服热载荷下刚度区域的驱离力，此时声载荷大小起主导作用，加筋板位移时间响应在屈曲后的2个平衡位置间做连续跳变运动，如图11(a)所示。随着温度逐渐升高，当声载荷强度与热载荷强度相当时，声载荷刚好可以克服热载荷下刚度区域的驱离力，此时声载荷与热载荷作用大小相当，位移时间响应在屈曲后的2个 平衡位置间做间歇跳变运动，如图11(b)、(c)所示。当温度继续升高，声载荷强度低于热载荷强度时，声载荷无法克服热载荷下刚度区域的驱离力，此时热载荷大小起主导作用，位移时间响应围绕屈曲后的一个凸面平衡位置做非线性的随机振动，如图11(d)所示。图11显示了屈曲后，位移时间历程由稀疏变得紧密；且固定条件下，位移响应与振动响应有较大差别，不同振动方向振幅相差也很大。

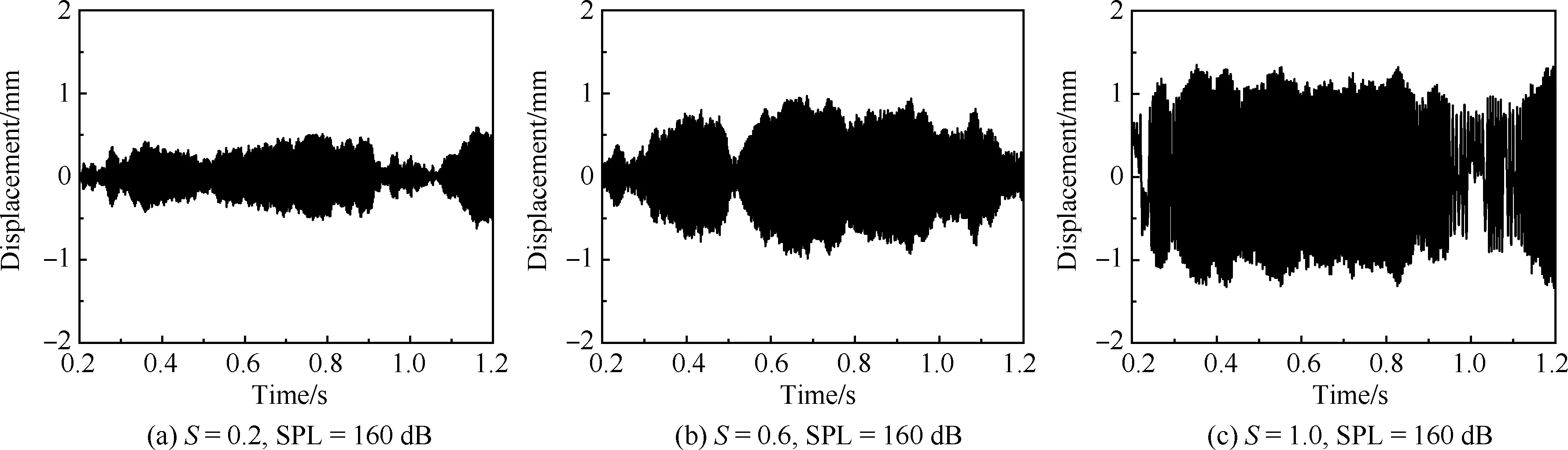
图10 屈曲前到临界屈曲不同声压级下横向位移时间历程Fig.10 Pre-buckling to critical buckling time history of lateral displacements under different SPLs

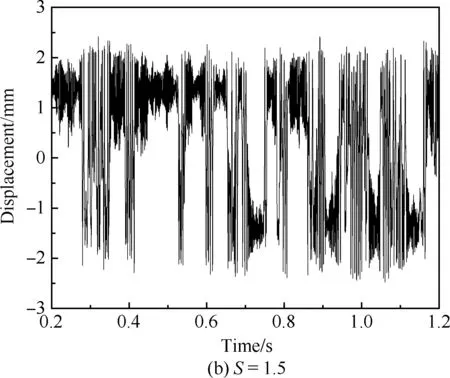
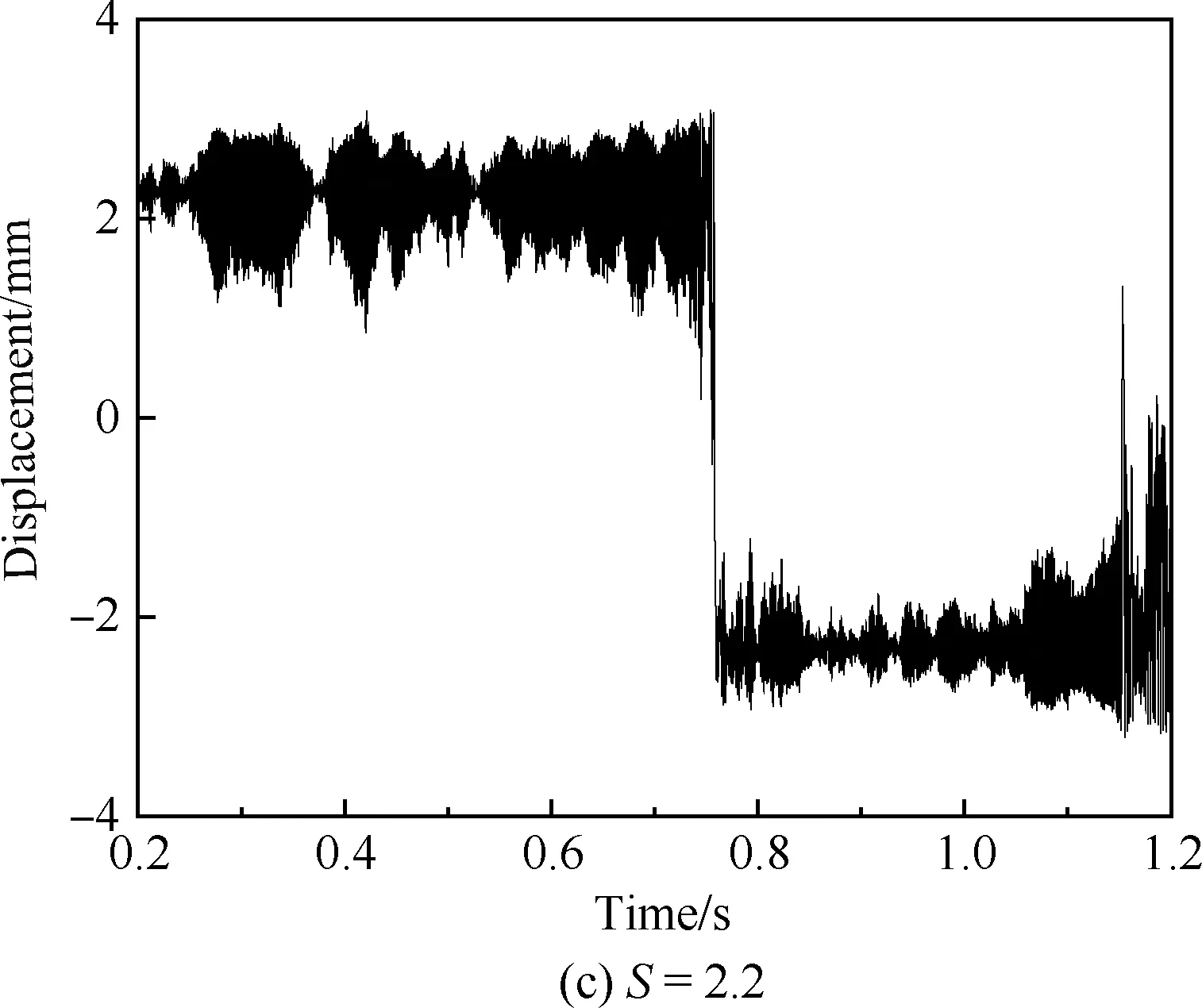
图11 屈曲后横向位移时间历程(SPL=172 dB)Fig.11 Time history of post-buckling lateral displacements (SPL=172 dB)

如图12所示，屈曲前，结构横向位移的概率密度函数(PDF)基本服从正态分布，如图12(a)、 (b)所示。随热载荷的增大，结构横向位移PDF不再服从正态分布，非线性响应逐渐增加。在临界屈曲温度附近时，非线性响应明显增强，加筋板开始在图12(c)所示的2个振动平衡位置之间进行往复振动。屈曲后，横向位移PDF明显呈现双峰现象，如图12(d)所示，可以得出，加筋板在凸面平衡位置周围的振动概率比在凹面平衡位置附近的振动概率更大，表明了声载荷的增加会在凸面平衡位置较好地驱动势能阱深度的增加。因此，加筋板更可能在凸面平衡位置周围进行随机振动。当热载荷与声载荷相当时，由于热载荷的加剧，凹面平衡位置中的势能阱深度增大，使加筋板在凹面平衡位置附近振动的可能性更大，如图12(e) 所示。随着温度持续升高，由于热载荷的增加，势能阱深度更大，从而引起振动响应平均值增加而振幅减小，并在一个屈曲后平衡位置附近产生非线性振动，如图12(f)所示，横向位移的PDF逐渐趋于正态分布，而非线性响应减弱。

图13给出了屈曲前和屈曲后结构横向位移的功率谱密度(PSD)。分析表明，在前屈曲区域，随着温度的升高加筋板的PSD幅值增大，而基频降低，即呈现峰值左移现象；PSD出现高频响应峰值，峰值随着热载荷的增加而增加，在临界屈曲附近达到最大值，如图13(a)所示。显然，在屈曲前，由于热应力的增加，加筋板进入软化区域，刚度降低，导致振动响应增大。然而，与屈曲前的响应结果相比，屈曲后PSD出现了低频响应峰值，而且随着热载荷的增加，响应峰值降低，加筋板的基频升高，如图13(b)所示。这表明在屈曲后，由于热应力的增加，加筋板进入硬化区域且刚度增强，因此振动响应也随之减小。

图12 横向位移的概率密度函数(PDF)(SPL=172 dB)Fig.12 Probability Density Function (PDF) of lateral displacement(SPL=172 dB)

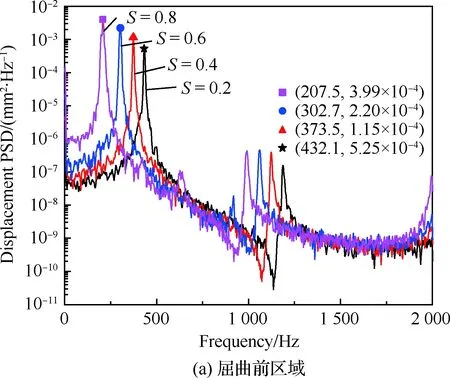
图13 横向位移功率谱密度(PSD)(SPL=151 dB)Fig.13 Power Spectral Density (PSD) of lateral displacement (SPL=151 dB)

3.2 应力分量响应分析

图14显示了在加筋板中心位置提取的x方向应力分量的时间历程。它具有以下几点特征：

1)x方向应力分量时间历程的振动平衡位置逐渐偏离横轴。从图14(a)可见，在临界屈曲温度条件下，平衡位置偏离值为y=-20 MPa，且温度越高，偏移量越大。拉应力和压应力同时存在并交替作用在加筋板上，而此时压应力为主导因素。

2) 如图14(b)所示，加筋板在x方向应力响应做间歇跳变运动过程中，当加筋板在凸面平衡位置周围振动时，x方向应力分量的振幅较大而平均值较小；而在凹面平衡位置周围振动时，x方向应力分量的振幅较小而平均值较大。如图14(b)、 (c)所示，随着温度的升高，x方向应力分量在2个平衡位置处的振幅减小而平均值增大。从S=1.5到S=2.2，2 个平衡位置处的振幅最大值从约为130 MPa减小到约为90 MPa；平均值从约为90 MPa增大到160 MPa。

3) 图14(d)表明，当热载荷足够大时，加筋板在凸面平衡位置附近振动，使x方向应力的幅值显著降低而平均值增大，此时加筋板主要表现出拉应力。

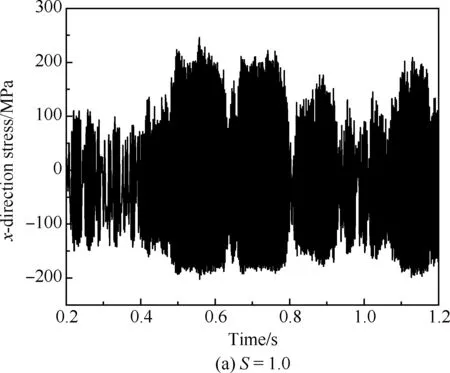
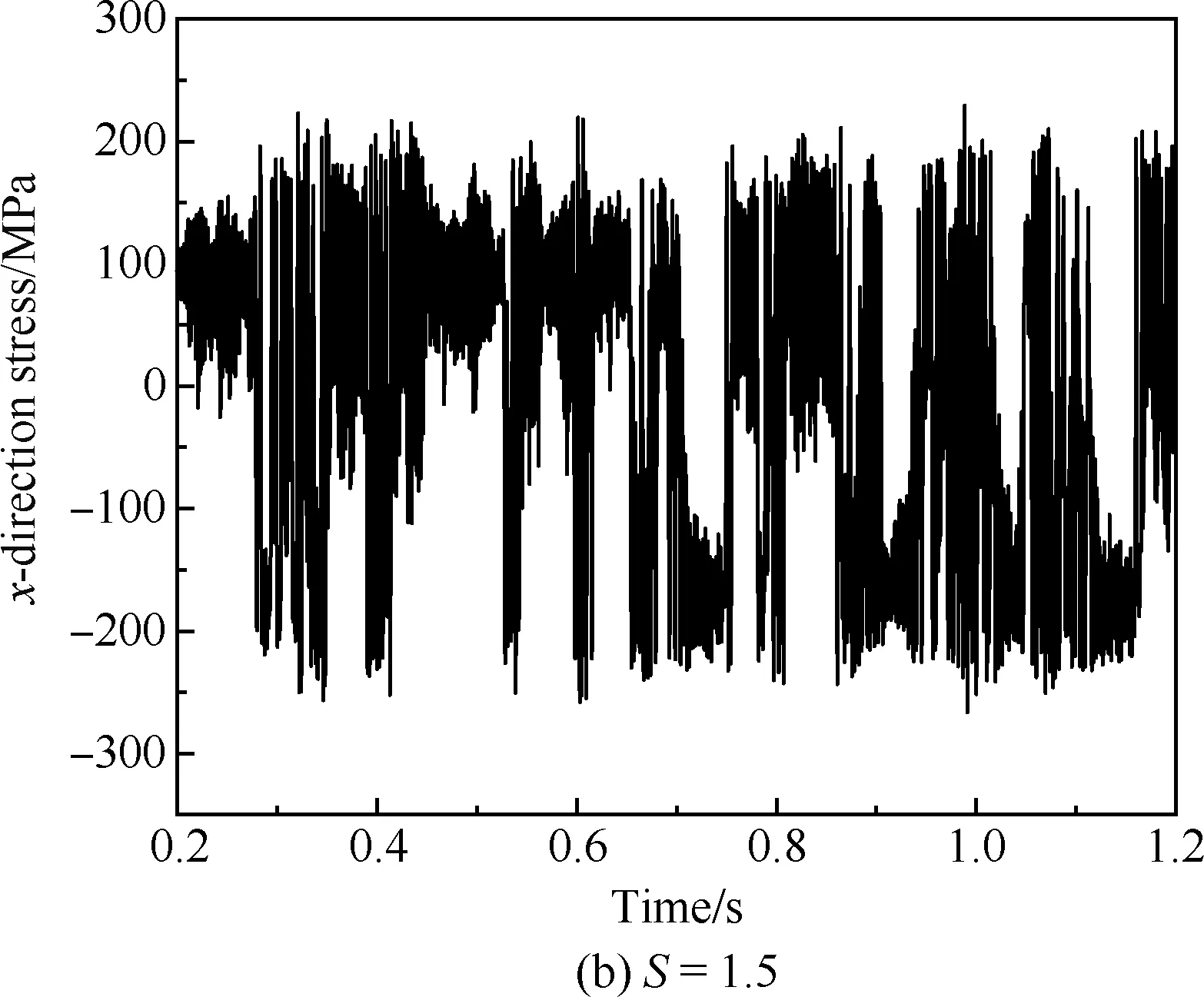
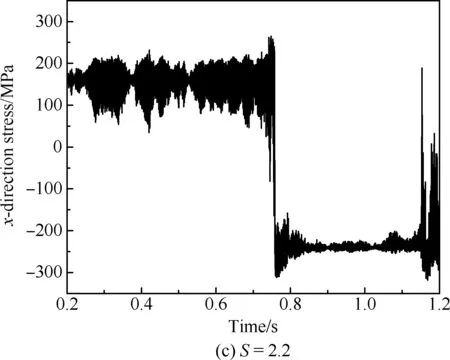
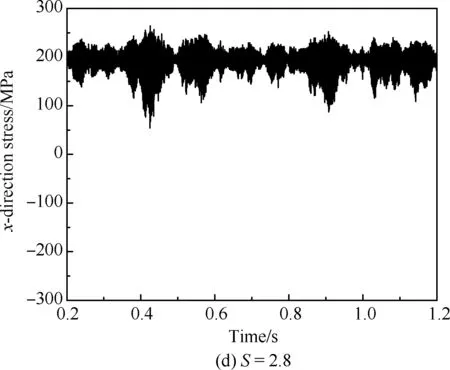
图14 屈曲后x方向应力时间历程(SPL=172 dB)Fig.14 Time history of post-buckling x-direction stress(SPL=172 dB)

4 结 论

1) 选择四边固支薄壁金属板进行热声载荷作用下动力学响应试验，并比较仿真与试验的热模态频率，证实了结果的一致性。然后比较了应变响应值，结果表明应变响应的仿真值与试验值在相同的数量级下比较吻合，得以验证了在热声载荷环境下薄壁板的非线性动力学响应模型和计算方法的有效性。

2) 本文完成了不同热声载荷大小组合情况下交叉加筋板的动力学响应计算。通过分析横向位移响应，可以得出以下结论：由于热应力的增大，在屈曲前，基频在软化区域逐渐降低，由于响应的高斯分布，SPL=172 dB时位移峰值由2.1 mm逐渐增大到2.6 mm，使加筋板在初始平衡位置周围随机振动；在屈曲后，基频在硬化区域逐渐增加，加筋板产生了由热载荷与声载荷的相对强度决定的跳变运动，同时考虑到响应的非高斯分布，加筋板显示出具有2个势能阱的双峰现象。

3) 当加筋板在2个平衡位置间振动时，拉应力和压应力交替作用，S=2.2, SPL=172 dB，结构x方向应力分量由拉应力(45～255 MPa)跳变为压应力(150～300 MPa)，x方向应力分量显示加筋板跳变形态。当受到较强的热载荷时，加筋板将围绕2个平衡位置中的一个振动，S=2.8, SPL=172 dB，x方向应力分量为50～250 MPa，加筋板完全进入受拉区域。

航空航天薄壁结构热声载荷作用下非线性响应分析十分复杂，本文只是初步探究，需要大量理论、模拟，特别需要进行针对更多典型结构的复杂热声载荷试验，获取大量试验数据，为进一步工程应用提供参考依据。