涡桨飞机螺旋桨滑流气动干扰效应及流动机理

赵帅，段卓毅，李杰,*，钱瑞战，许瑞飞

1. 西北工业大学 航空学院，西安 710072 2. 航空工业第一飞机设计研究院，西安 710089

涡桨飞机具有起降距离短、经济性好等优势，至今仍在军民用航空领域占据重要地位。进入21世纪以来，各国仍在投入力量研发新型号的涡桨飞机。与喷气式飞机不同，涡桨飞机在设计过程中面临着螺旋桨滑流气动干扰这一特殊问题。螺旋桨滑流是桨叶在运转过程中产生的高速、旋转气流。在滑流的影响下，飞机的升阻特性、失速特性及力矩特性都会发生变化[1-2]。因此，深入研究滑流气动干扰效应及其背后的流动机理，对涡桨飞机的研发具有重要的意义。

国外关于滑流影响的研究起步较早，研究内容也比较丰富。Borne和Hengst[3]通过飞行实验测量了福克50飞机机翼、短舱、平尾的表面压力分布及平尾附近的动压和下洗角，并与风洞试验结果和计算结果进行了对比；Moens和Gardarein[4]采用基于激励盘模型的准定常方法研究了滑流对机翼及增升装置的影响；Stuermer[5]采用基于嵌套网格技术的非定常方法模拟了螺旋桨与机翼的相互干扰；Schroijen等[6]采用多种计算方法并结合试验数据研究了滑流对垂尾的影响；Roosenboom等[7-8]运用粒子图像测速(PIV)技术对某型运输机的滑流流场进行了精确的测量。与国外相比，国内对滑流问题的研究起步较晚，而且已有研究多侧重于滑流在小迎角下对机翼、增升装置的干扰及升阻特性的影响[9-13]。关于滑流对机翼大迎角分离特性及平垂尾影响的研究仍然比较缺乏。

本文采用基于动态面搭接网格技术的非定常方法，对某双发涡桨飞机巡航状态下的气动特性进行了模拟。全面分析了滑流影响下飞机升、阻力及俯仰力矩、滚转力矩和偏航力矩的变化情况，并在此基础上研究了滑流对机翼及平垂尾的影响及流动机理。

1 数值方法

1.1 控制方程及其离散

采用有限体积法离散求解三维可压缩非定常RANS (Reynolds-Averaged Navier-Stokes)方程；黏性项采用二阶中心差分格式离散；无黏项通量离散采用Roe格式和3阶MUSCL(Monotone Upstream-centered Schemes for Conservation Law)插值方法；湍流模型为一方程SA (Spalart-Allmaras)模型；时间推进项采用隐式LU-SGS (Lower-Upper Symmetric Gauss-Seidel)双时间法，并应用当地时间步长和多重网格等措施加速计算的收敛。

1.2 搭接面通量插值算法

动态面搭接算法的基本原理是将流场划分为包围螺旋桨的圆柱形区域及外部静止区域两部分，在计算过程中包围螺旋桨的圆柱形区域网格绕旋转轴转动，两区域在搭接面上进行通量的双向插值。

r=a1+a2ξ+a3ζ+a4ξζ

(1)

式中：a1、a2、a3和a4为坐标转换系数。

采用牛顿迭代法求解式(1)即可得到目标网格单元中心的坐标(ξj,ζk)。然后搜索距离(ξj,ζk)最近的源网格单元(ξm,ζn)。网格单元间的距离定义为

L=(ξj-ξx)2+(ζk-ζy)2

(2)

最后，通过求解式(3)即可确定(ξj,ζk)处的通量：

(DζC(2))m,n(ζk-ζn)

(3)

2 模型及网格

本文研究对象为某双发涡桨支线客机，其计算模型如图1所示，该模型包含了机身、机翼、垂尾、平尾、发动机短舱、螺旋桨和襟翼滑轨整流罩等部件，两侧的螺旋桨均为顺时针旋转(飞行员视角)。

采用ICEM-CFD划分多块结构网格，近壁面首层网格高度满足y+≤1。为了保证左右两侧网格一致性，首先生成半模的网格，然后通过镜像、平移等操作生成全模网格。带动力构型静止域网格数量约为6 900万，旋转域网格数量约为600万，网格总数约为7 500万。保持静止域的网格拓扑结构及节点分布规律不变，在旋转域内去掉螺旋桨部件重新进行网格划分，生成无动力构型的网格。计算网格如图2和图3所示。

图1 背景飞机计算模型Fig.1 Computational model of reference aircraft

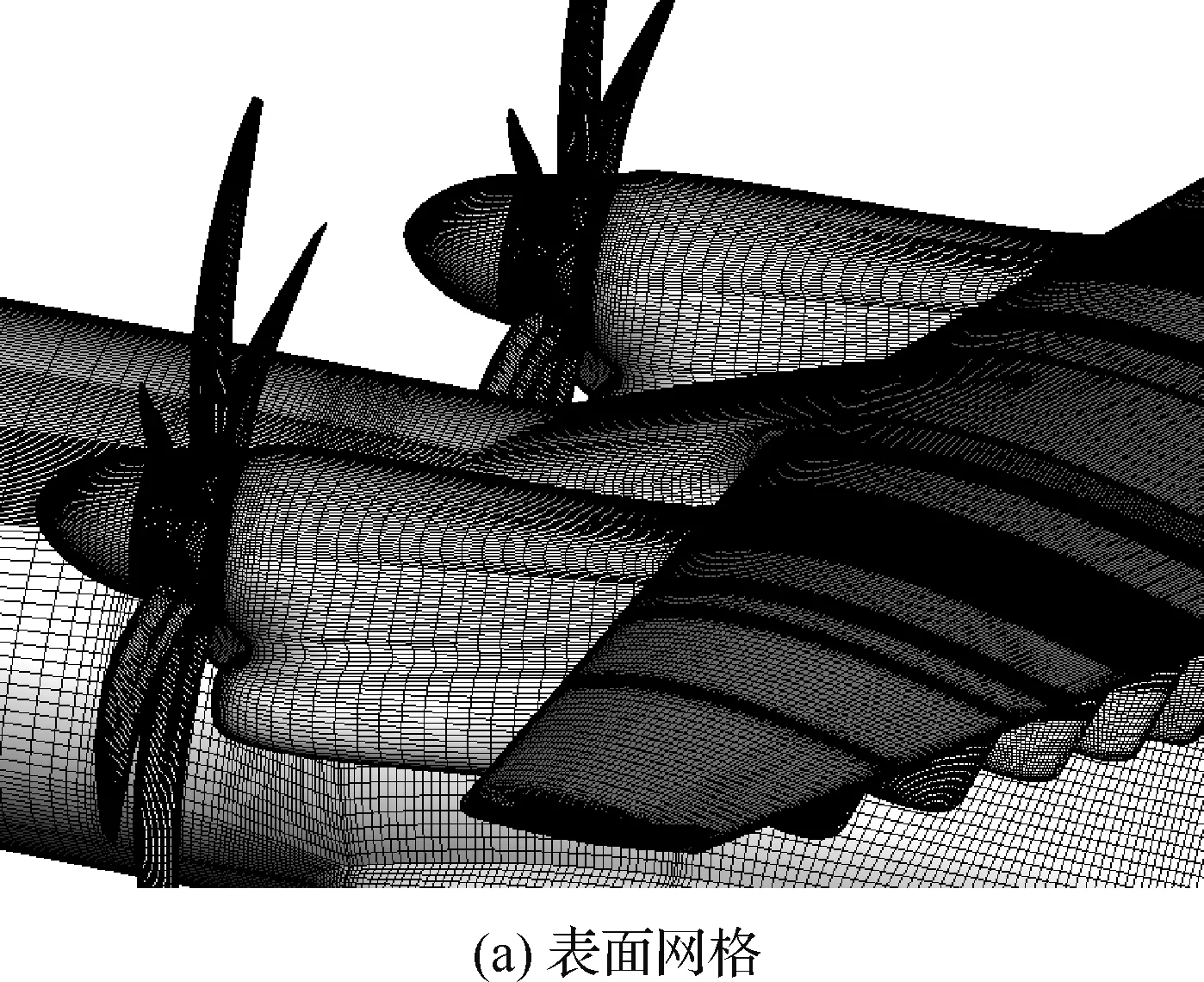
图2 带动力构型计算网格Fig.2 Computational grid for powered configuration

图3 无动力构型计算网格Fig.3 Computational grid for unpowered configuration

3 计算结果与分析

3.1 计算与试验的对比

背景飞机在德国-荷兰的DNW-LLF大型低速风洞8 m×6 m试验段开展了测力测压试验，试验模型为1∶6的缩比模型。计算模型与试验模型相同，计算参数与试验保持一致：自由来流马赫数为0.2，基于机翼平均气动弦长的雷诺数约为200万，侧滑角为0°。带动力构型螺旋桨前进比为1.7，对应的单桨拉力系数约为0.05，拉力系数定义为

(4)

式中：T为拉力；ρ和V∞分别为来流的密度和速度；S为机翼面积。

带动力构型采用非定常方法进行计算，每个物理时间步螺旋桨转动0.25°，即一个旋转周期内迭代1 440 步，牛顿子迭代步数取10 步，通过监测气动力系数来判断收敛情况，每个状态需要计算10～14 个周期。本文计算在国家超算广州中心的天河2号上完成，天河2号每个节点包含24个CPU核，采用2个节点并行计算，一个旋转周期大约需要30 h。图4展示了0°迎角下全机气动力在螺旋桨旋转一周内的波动情况，图中横坐标Ψ为相位角，CL、CD、Cl、Cm和Cn分别为升力、阻力、滚转力矩、俯仰力矩和偏航力矩系数。由于背景飞机采用了6叶螺旋桨，气动力在一周内呈现6次规律性的波动。

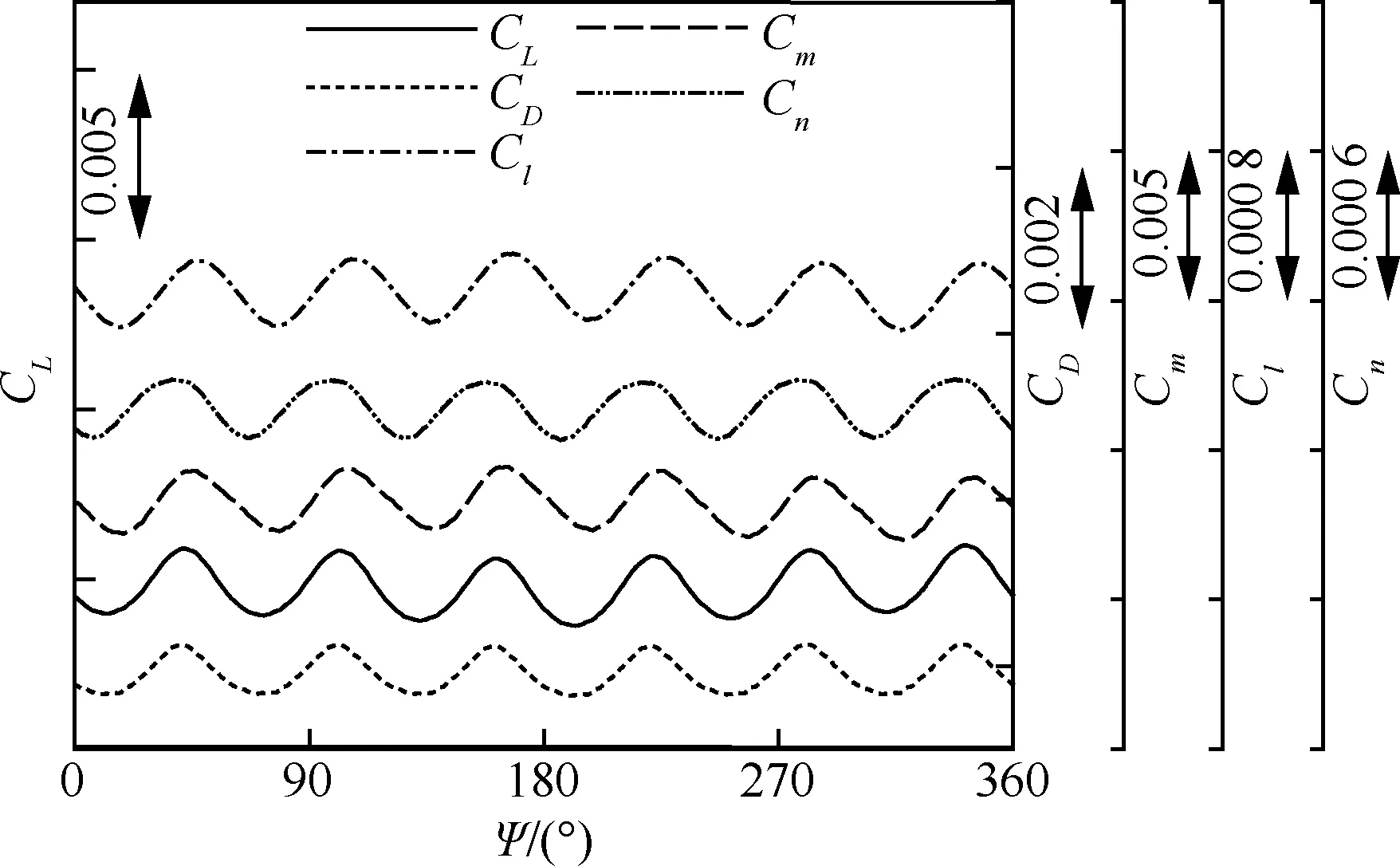
图4 一个旋转周期内气动力系数变化情况 (α=0°)Fig.4 Variation of aerodynamic coefficients during one rotation(α=0°)

滑流影响下的全机气动力具有典型的非定常特征，为了与试验结果对比，需要在计算收敛后对一个周期内的气动力进行平均。图5展示了带动力构型及无动力构型的气动力计算结果与风洞试验结果的对比。其中，带动力构型的气动力为扣除螺旋桨直接力(包括螺旋桨拉力、扭矩、径向力等)后的全机气动力。从图中可以看到，在滑流影响下，全机升力系数和阻力系数有所增加，升阻比和纵向静稳定度有所降低。但由于巡航状态下螺旋桨拉力系数较小，气动力变化的幅度并不大。计算精度方面，在-3°～8°迎角的线性段内，带动力构型升力系数计算误差不超过3%，纵向静稳定度计算误差不超过5%，阻力系数计算误差稍大，最大误差达到了16%。阻力系数误差较大的原因是计算采用了全湍假设，导致摩擦阻力明显高于试验结果。

受滑流影响，飞机会在无侧滑时产生滚转力矩与偏航力矩，但由于其量值非常小，很难进行准确的预测。从图5(e)和图5(f)可以看到，虽然在具体量值有一定的差异，但计算得到滚转力矩系数和偏航力矩系数随迎角的变化趋势与试验基本保持了一致。从-3°～17°，滚转力矩系数先增大后减小然后再增大，整条曲线存在2个比较明显的拐点。试验得到的曲线拐点位置为1.4°和16°，计算得到的曲线拐点位置为0°和16°。偏航力矩系数的变化趋势与滚转力矩相反，在-3°～17°范围内，偏航力矩系数先减小后增大然后再减小。偏航力矩曲线同样存在2个比较明显的拐点，试验得到的曲线拐点位置为0.6°和16°，计算得到的曲线拐点位置为2°和14°。

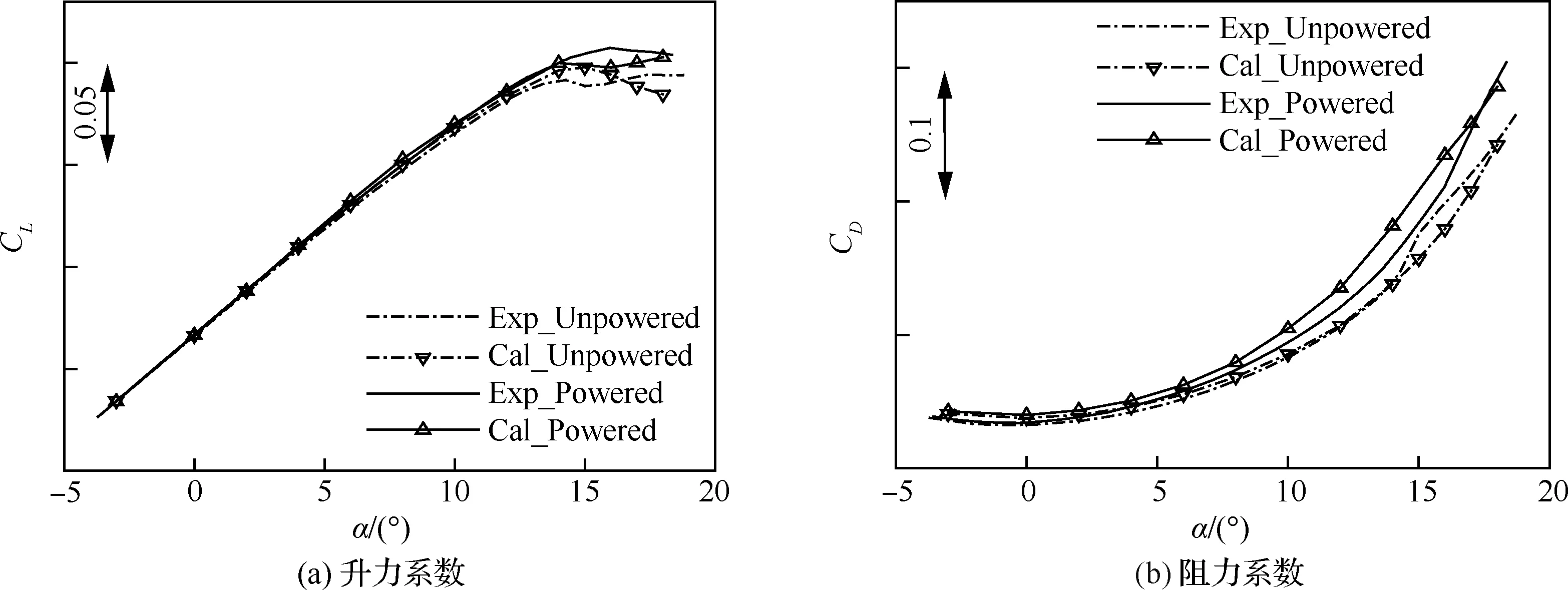
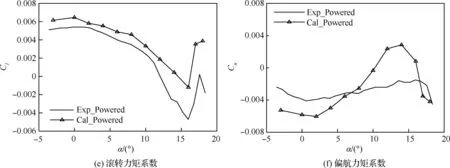
图5 有/无动力构型气动力计算值与试验值的对比Fig.5 Comparison of calculated and experimental aerodynamic coefficients for powered and unpowered configurations

图6展示了6°迎角下的全机表面压力云图，可以发现在滑流的影响下左右两侧机翼的压力分布出现了明显的非对称性。图7～图9分别给出了机翼、平尾和垂尾部分截面表面压力系数Cp计算结果与试验值的对比，截面位置见图6(b)，η为展向相对位置,x/c为采用当地弦长无量纲后的x坐标，坐标原点是当地站位翼型前缘点。其中机翼-17.8%和46.9%截面处于滑流的下洗影响区，17.8%和-46.9%截面处于滑流的上洗影响区。可以看到，在机翼及平垂尾的各个截面位置处，计算结果都与试验结果高度吻合，表明本文采用的非定常方法具有良好的计算精度。

图6 表面压力云图(α=6°)Fig.6 Surface pressure contours(α=6°)

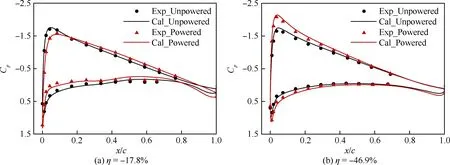
图7 机翼表面压力系数分布计算结果与试验值的对比(α=6°)Fig.7 Comparison of calculated and experimental pressure coefficient distributions on wing surface(α=6°)

图8 平尾表面压力系数分布计算结果与试验值的对比(α=6°)Fig.8 Comparison of calculated and experimental pressure coefficient distributions on horizontal tail surface(α=6°)

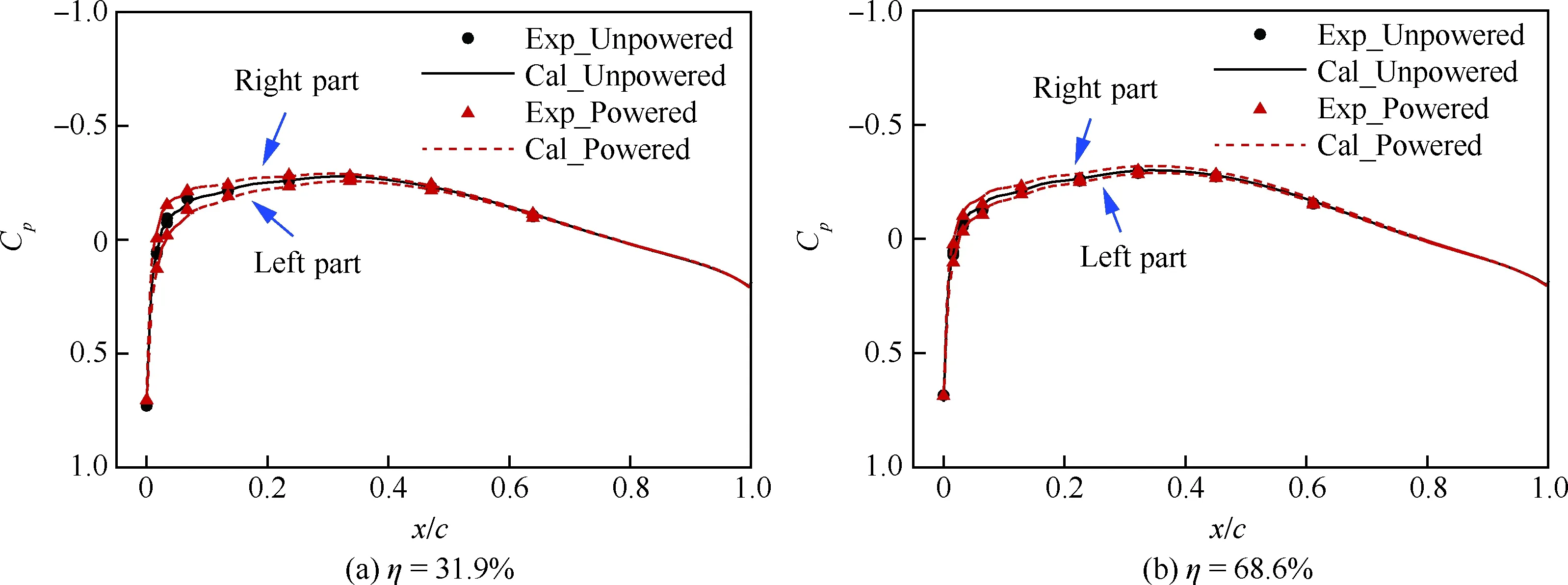
图9 垂尾表面压力系数分布计算结果与试验值的对比(α=6°)Fig.9 Comparison of calculated and experimental pressure coefficient distributions on vertical tail surface(α=6°)

3.2 滑流对机翼的影响及机理分析

滑流在小迎角下对机翼影响的研究已经比较成熟[15-17]，因此本文主要关注滑流在大迎角下对机翼翼面分离特性的影响。图10展示了14°迎角下带动力构型及无动力构型的全机表面极限流线，图中用蓝色直线标明了测压截面的位置。通过对比可以发现，在螺旋桨下行运动一侧，滑流有效抑制了翼面的流动分离；在螺旋桨上行运动一侧，翼面的流动分离却并未得到明显的改善。从图11 可以看到，计算所反映出的滑流对各截面分离位置的影响趋势与试验基本保持了一致，表明图10 所展示的翼面分离形态是合理的。仔细观察各截面的压力分布可以发现：在-17.8%截面和35.3% 截面，分离区域消失；在-35.3%截面，流动分离得到了轻微的改善；而在17.8%和-46.9%截面，分离点的位置反而比无滑流时更为提前。这些结果说明，虽然滑流提高了升力系数，但滑流对翼面流动分离的影响并不都是有利的。另外，从表面流线对比可以看到，滑流影响下46.9%截面附近分离区范围扩大。通过分析该截面的压力分布发现，试验结果反映出滑流确实会导致该截面分离点位置前移，这种变化趋势与计算结果相同，只是计算得到的分离点的前移量要比实验大。这种现象是由于该截面处于滑流流管的边界位置，而滑流内部与外部区域在速度的大小和方向上存在较大差异，此速度差将在滑流边界上产生强烈的剪切效应，在大迎角这种流动不稳定状态容易诱导翼面发生流动分离。

螺旋桨下行运动一侧(对应滑流的下洗区)流动分离被有效抑制主要是因为滑流的旋转减小了当地迎角，推迟了流动分离。而在螺旋桨上行运动一侧(对应滑流的上洗区)，滑流的旋转增大了当地的迎角，加重了分离的趋势。图12给出了螺旋桨下游X/D=0.8截面处的无量纲流向速度云图，X为该截面与螺旋桨旋转平面间的距离，D为螺旋桨直径。虽然滑流可以为附面层注入能量，延迟流动的分离，但从图中可以看到，在上行运动一侧，螺旋桨对气流的加速效果并不明显，桨后气流的流向速度只略高于自由来流的流向速度，这部分增加的能量无法消除当地迎角增加带来的不利影响。与之相比，在螺旋桨下行运动一侧，桨后气流的流向速度明显高于自由来流的流向速度，其对分离的抑制效果要更好。从图11的压力分布可以看到，带动力条件下，-17.8%和35.3%截面驻点压力(正压峰值)要高于17.8%和-35.3%截面。

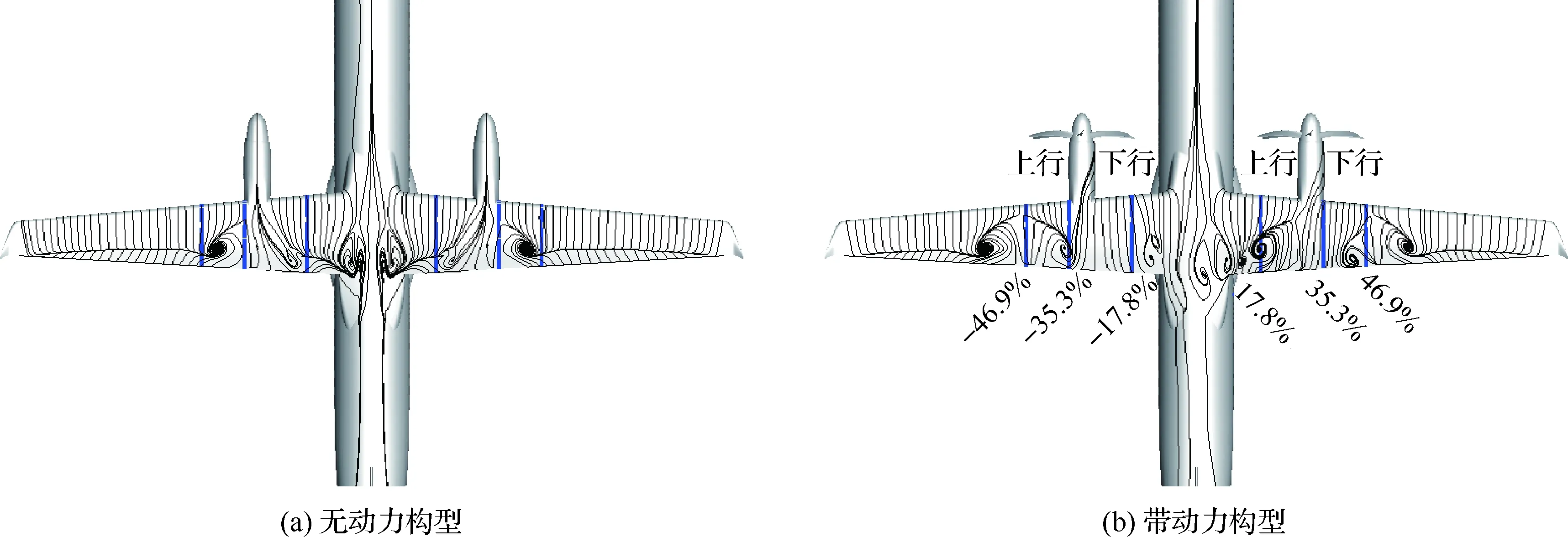
图10 表面极限流线(α=14°)Fig.10 Surface-restricted streamlines (α=14°)

图11 机翼表面压力系数分布计算结果与试验值的对比(α=14°)Fig.11 Comparison of calculated and experimental pressure coefficient distributions on wing surface(α=14°)

上行和下行桨叶后方气流速度的差异是由桨盘载荷分布的非均匀性引起的。文献[5]的研究表明：在正的来流迎角下，下行桨叶当地速度及迎角相对于0°迎角状态会增加，上行桨叶当地速度及迎角会减小。因此，在正迎角下，下行桨叶的载荷要高于上行桨叶的载荷，而更高的载荷意味着桨叶对气流做功更大，桨后气流速度必然更高。从图13可以看到，在14°迎角下，下行桨叶前缘低压区要显著强于上行桨叶前缘低压区。

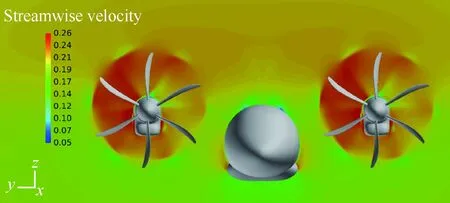
图12 螺旋桨下游X/D=0.8截面处无量纲 流向速度云图(α=14°)Fig.12 Dimensionless streamwise velocity contours at X/D=0.8 cross-section behind propeller (α=14°)

图13 表面压力云图(α=14°)Fig.13 Surface pressure contours(α=14°)

3.3 滑流对平尾的影响及机理分析

平尾对全机俯仰力矩和纵向静稳定度有着决定性的影响。图14展示了-3°～8°迎角范围内平尾俯仰力矩系数变化情况。在滑流影响下平尾俯仰力矩曲线斜率减小，即平尾效率降低。通过曲线拟合计算得到平尾效率下降量约为2.7%。文献[18-19]指出，滑流对平尾效率的影响分为两个方面。一方面，由于滑流提高了机翼的升力线斜率，使得平尾当地的下洗角变化率增加，导致平尾效率降低；另一方面，在某些情况下，滑流会直接覆盖平尾的部分或全部区域，增加当地的动压，进而提升平尾的效率。任晓峰[20]、王伟[21]等通过降低平尾的安装位置，使平尾提早进入滑流区，显著地改善了全机的纵向静稳定度。

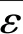
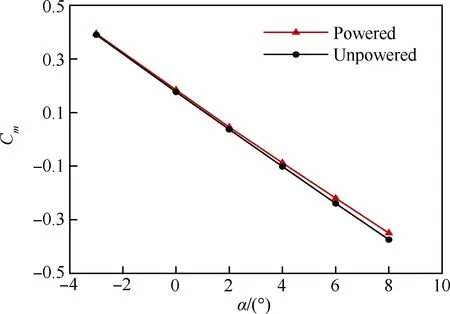
图14 有/无动力构型平尾俯仰力矩系数对比Fig.14 Comparison of pitching moment coefficients of horizontal tail for powered and unpowered configurations

图15 下洗角及动压监测点分布Fig.15 Distribution of monitoring points of downwash angle and dynamic pressure

从表1可以看出，在-3°～8°迎角范围内，有/无动力构型的平尾当地动压差异不超过0.2%，滑流对动压的影响几乎可以忽略。这主要是因为背景飞机采用了T型尾翼，平尾安装位置较高且距离发动机较远，滑流无法覆盖平尾。从图16可以看到，带动力构型平尾当地的下洗角随迎角的变化率要明显大于无动力构型。由于当地动压没有提升，下洗角变化率的增加必然会导致平尾效率下降。

表1不同迎角下的无量纲速压平均值

Table1Averagevaluesofdimensionlessdynamicpressureatdifferentanglesofattack

α/(°)QUQPΔQ/%-30.0192440.019253-0.048800.0191450.0191330.063020.0190960.0190700.136440.0190640.019086-0.117760.0190380.019045-0.035980.0190250.0190070.0981

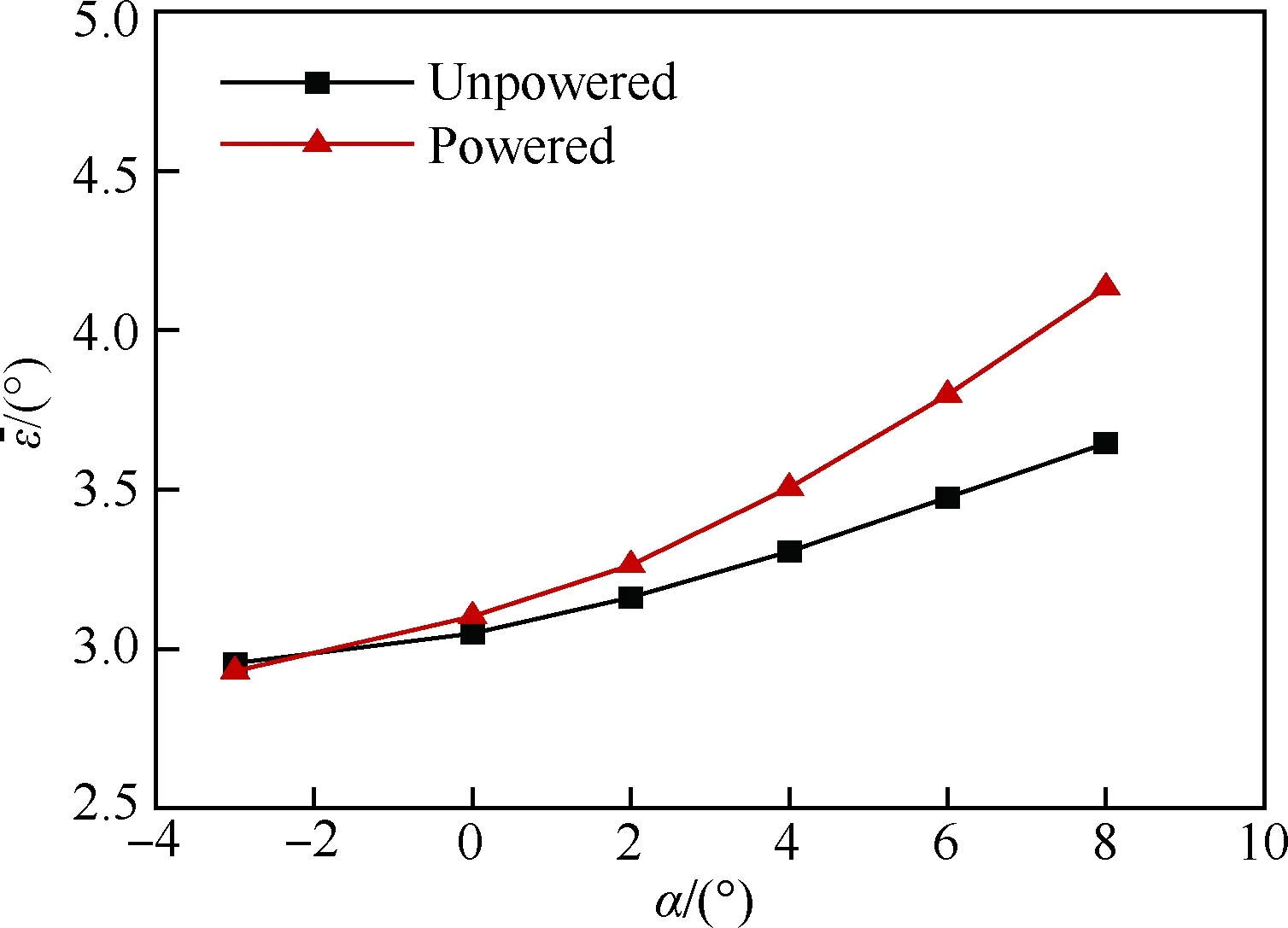
图16 下洗角平均值随迎角变化情况Fig.16 Variation of average values of downwash angle as a function of angles of attack

3.4 滑流对垂尾的影响及机理分析

滑流在向下游的发展过程中会产生横向的移动，从而对垂尾的流动造成影响，这种影响称为滑流的侧洗效应。图17展示了2°迎角下的滑流流场结构，可以看到，滑流在流经机翼后逐渐向右侧(y轴正向)偏斜。向右侧偏斜将使得垂尾产生正的侧力与负的偏航力矩，这与图18的气动力计算结果是吻合的，CY为侧力系数。

Schroijen等[6]指出，滑流的侧洗与左右两侧机翼升力分布的不对称性有关。滚转力矩是反映机翼升力不对性的重要指标。从图18可以看到，平尾的侧力曲线与偏航力矩曲线均出现了2个较为明显的拐点，拐点位置为2°和14°，与3.1节介绍的全机滚转力矩曲线拐点的位置非常接近，这也从侧面印证了文献[6]的有关结论。

图17 螺旋桨滑流流场结构(α=2°)Fig.17 Flow structure of propeller slipstream(α=2°)

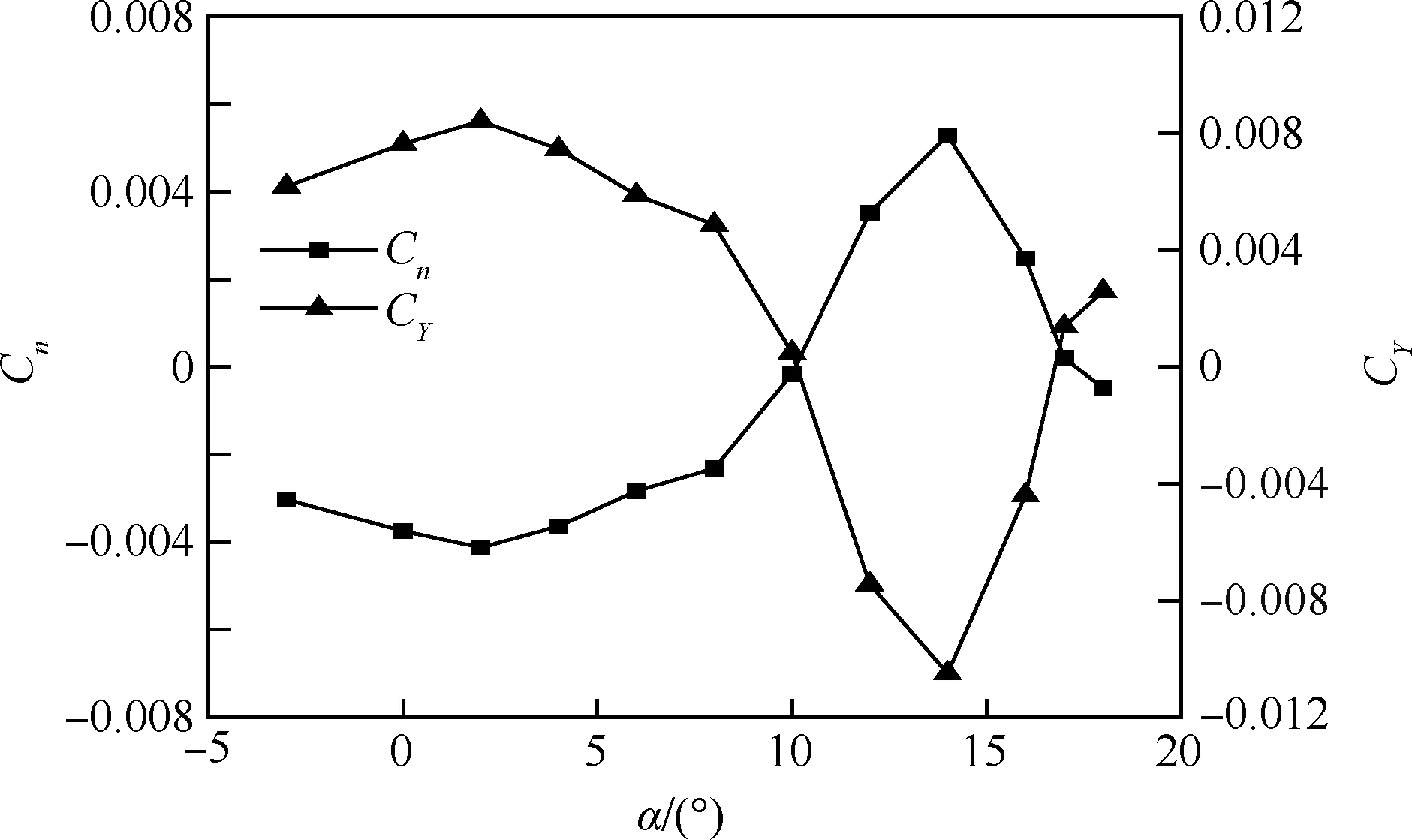
图18 垂尾偏航力矩系数及侧力系数随迎角变化情况Fig.18 Variation of yawing moment coefficients and lateral force coefficients of vertical tail as a function of angles of attack

4 结 论

1) 本文的计算方法能够较为准确地评估滑流对气动力及表面压力分布的影响。

2) 在滑流影响下，全机升力系数和阻力系数有所增加，升阻比和纵向静稳定度有所降低，并在无侧滑时产生了滚转力矩和偏航力矩。

3) 在螺旋桨下行运动一侧，滑流的旋转减小了当地迎角，同时桨后气流速度较高，翼面流动分离得到了有效抑制；而在螺旋桨上行运动一侧，由于滑流的旋转增大了当地迎角，而且桨后气流速度较低，翼面流动分离并未得到明显改善。

4) 背景飞机平尾效率下降的主要原因是滑流提高了机翼的升力线斜率，导致平尾当地下洗角变化率增加。

5) 垂尾的侧力与偏航力矩是由滑流的侧洗引起的，而滑流的侧洗与左右两侧机翼升力分布的不对称性有关。