超临界自然层流机翼设计及基于TSP技术的边界层转捩风洞试验
张彦军,段卓毅,雷武涛,白俊强,徐家宽
1. 航空工业第一飞机设计研究院,西安 710089 2. 西北工业大学 航空学院,西安 710072
随着环境保护形势的日益严峻,国际航空运输协会提出了航空工业减少排放物和降低噪声的新要求。而能够实现这一目标的相关关键技术当中,气动减阻技术成为空气动力学设计者重点研究的对象。随着航空工业设计技术和制造工艺的突飞猛进,层流流动设计逐步成为可能。对于民用客机而言,层流机翼设计技术(机翼、垂尾、平尾)和层流短舱设计技术可以降低摩擦阻力30%左右,即提高巡航效率15%左右。气动收益非常明显,提升气动性能的同时减少燃油消耗和污染物排放以及降低噪声。
在20世纪80年代,美国和欧盟在自然层流机翼和混合层流机翼方面进行了大量的理论研究、风洞试验验证和飞行试验验证[1-3]。比较有代表性的是:Boeing公司在B757上的层流减阻研究,欧盟在SAAB 2000飞机的机翼上进行的层流控制飞行试验验证和在A320垂尾上进行的飞行试验验证。Falcon50飞机飞行试验是进行混合层流设计项目研究的一部分,目的是在未来商用飞机的飞行马赫数、雷诺数和后掠角范围内研究层流控制的可行性。在国外进行的层流设计研究和案例当中,德国宇航研究院(DLR)早在20世纪80年代就开始进行了前掠翼布局自然层流飞机(Forward Swept Wing-Natural Laminar Flow:FSW-NLF)的研究[4]。随着现代工业的发展,满足层流流动对表面波纹度、光洁度等加工要求的机体可以实现,自然层流设计也终于应用到了工程上面。Honda Jet轻型公务机采用自然层流机身头部和自然层流机翼[5-6],于2003年成功首飞并达到预期的设计目标和要求。2006年,意大利Piaggio Aero Industries公司的研究人员与意大利宇航研究院合作提出了一种跨声速自然层流超临界机翼设计方法,并且基于此制作了相应的风洞模型,命名为UW-5006自然层流机翼,进行了风洞试验[7-8]。2010年,波音公司和美国国家航空航天局(NASA)进行了高雷诺数后掠机翼自由转捩风洞试验,分别在美国NTF(National Transonic Facility)和欧洲ETW(European Transonic Windtunnel)风洞进行温敏涂层转捩测量试验,研究不同雷诺数下TS (Tollmien-Schlichting)波和横流(Crossflow)波主导的转捩,并研究了模型表面加工粗糙度对横流驻波诱导转捩的影响[9]。
中国对超临界自然层流设计的研究仍然处于比较初步的阶段。西北工业大学的乔志德[10]研究了自然层流超临界翼型的设计方法,解决了维持层流所需的有一定顺压梯度压力分布形态和无激波超临界翼型的屋顶状压力分布要求的矛盾,为自然层流机翼的设计奠定了基础。北京航空航天大学的额日其太等[11]针对层流控制在飞机减阻、外表面红外隐身方法以及抑制气动热的生成等方面进行了研究,分析和试验结果证明:前缘吸气具有很好的层流控制效果。孙智伟[12]、黄江涛[13-14]等进行了超临界翼型和机翼的优化设计研究,而针对超临界自然层流翼型,西北工业大学的乔志德等[15-16]进行了较为详细的设计思想、设计方法和风洞试验研究,清华大学的张宇飞等[17]针对超临界自然层流翼型和机翼进行了优化设计策略的研究。西北工业大学的韩忠华等[18]采用代理模型,对自然层流机翼进行优化设计研究。
在高精度边界层转捩预测方法方面,近些年来得到了长足的发展。其中,Langtry等[19-22]提出的基于经验关系式的输运方程转捩模式在机械流动和航空流动中应用广泛。另一种基于稳定性理论分析的半经验转捩预测方法是eN方法,该方法主要使用线性稳定性理论,描述小扰动行波——TS波的振幅沿边界层流向的线性放大阶段,并根据经验选定判定转捩发生的方法因子临界N值,从而预测低湍流度下的各类扰动波主导的转捩现象。eN方法最早在20世纪中期由Smith[23]和van Ingen[24]等发展而来,随后Gleyzes[25]和Drela[26]等进一步提出了近似包络方法。近似包络方法通过采用线性稳定性方法分析得到F-S(Falkner-Skan)速度型及其对应的扰动放大因子n与动量厚度雷诺数的曲线,并将其用数学描述,得到对应不同速度型的扰动放大因子包络线,将其作为转捩判断的数据库。2013年,Coder和Maughmer[27-28]基于前述数据库里的n因子与形状因子和动量损失厚度雷诺数的关系,构造出了流向扰动放大因子的输运方程,与Menterk-ωSST(Shear Stress Transport)湍流模式[29]耦合形成基于线性稳定性理论的湍流转捩模式。该方法所有变量均能够当地求解,与现代CFD大规模并行求解兼容,且具有高精度的稳定性分析基础。徐家宽和白俊强[30]使用标量输运方程的形式实现了包络近似方法中放大因子的当地化求解,实现了自然转捩和分离泡转捩的建模。
在边界层转捩试验研究方面,中航工业气动院的尚金奎等[31]对温度敏感材料涂层(Temperature Sensitive Paint, TSP)转捩预测试验技术进行了研究,采用TSP技术对某民机半模进行试验,预测转捩位置,并通过与红外试验技术预测结果进行对比,验证了TSP试验方法的精度;北京大学的朱一丁等[32]采用瑞利散射流动显示、高频动态压力传感器以及粒子图像测速等方法,在北京大学高超马赫风洞中开展试验,对高超声速边界层转捩及湍流产生机理进行了研究。
当前,国内针对跨声速超临界自然层流机翼在高雷诺数下的边界层转捩试验研究非常罕见,面对未来绿色高效飞行器的设计需求,这一方面的研究急需进行和完善。本文对超临界自然层流翼型和机翼进行了设计,并应用高精度转捩预测方法进行气动特性评估,随后加工制造了高质量的风洞试验模型并进行了精细的高雷诺数边界层转捩风洞试验验证,与高精度转捩数值模拟结果进行对比分析,得到超临界自然层流机翼的边界层转捩特性,预期对该类型机翼的研究和发展起到一定的推动作用。
1 超临界自然层流机翼
1.1 超临界自然层流机翼的设计
自然层流机翼需要在合适的气动布局和设计约束下才能发挥最佳的减阻效果,如适当的飞行雷诺数、较小的机翼前缘后掠角、机翼上最好不要安装发动机等,因此研究背景飞机最终选定为尾吊布局喷气式飞机,设计目标为支线客机和公务机,其气动布局三面图,如图1所示,机翼平面形状和展向参数分布如图2所示。机翼的具体参数见表1。
需要指出的是全机升力系数为0.4,考虑配平损失后对翼身组合体构型设计升力系数定为0.42。 设计马赫数为0.75;前缘后掠角为17.5°,属于小后掠机翼范畴;设计飞行雷诺数为1.8×107左右。但考虑到风洞试验技术、研究经费等原因,可在风洞试验中验证的最大雷诺数在1×107左右,根据相关文献中大量的稳定性分析和飞行试验数据(如图3所示)可知,在该后掠角和雷诺数组合状态下,TS波失稳主导转捩,尚未出现横流不稳定性转捩。且试验风洞为低湍流度风洞,暂不考虑横流行波失稳。针对横流驻波主导的失稳,其扰动源主要是壁面粗糙度。自然层流机翼风洞试验模型应比普通测力测压的试验模型具有更高的光洁度,普通试验模型机翼表面粗糙度为Ra=0.8 μm,自然层流机翼风洞试验模型机翼表面粗糙度应达到Ra=0.4 μm,具有比较高的横流驻波失稳临界雷诺数,不容易发生该类型的转捩。因此,在进行机翼设计时暂不考虑横流不稳定性转捩,从而采用先进行基本翼型设计,再进行三维机翼设计的策略。

图1 背景飞机三面图Fig.1 Plane three-view layout

图2 机翼平面形状和参数分布Fig.2 Plane shape and parameters distribution of wing
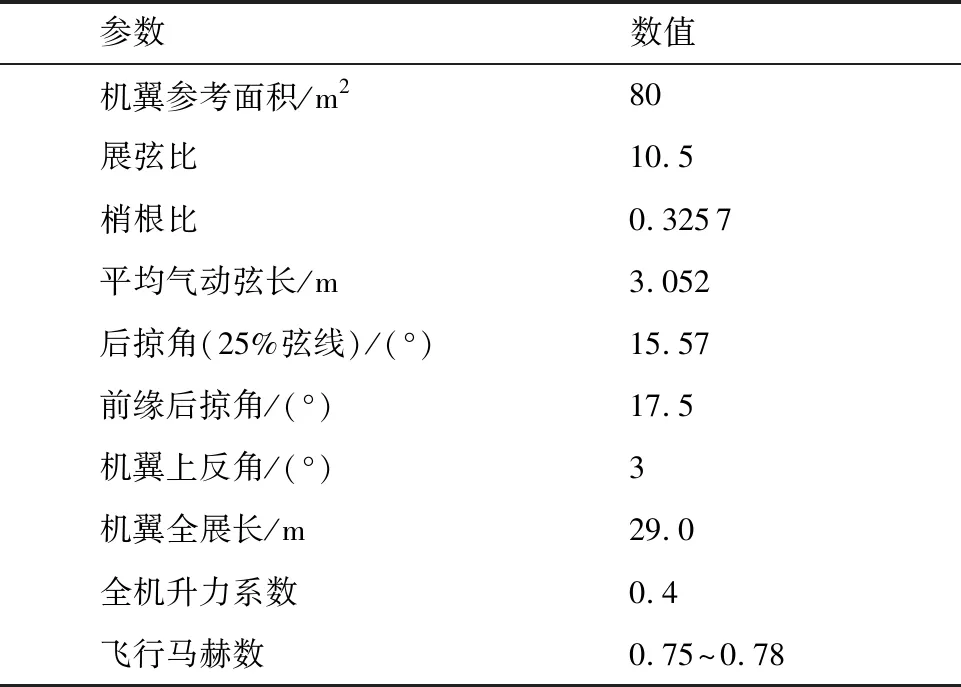
表1 机翼形状具体参数Table 1 Detailed parameters of wing
图3 飞行试验和稳定性分析结果总结而来的主导 失稳类型与前缘后掠角、雷诺数之间的关系Fig.3 Relations among dominated instability mode, leading edge swept angle and Reynolds number from the results of flight test and stability analysis
机翼飞行雷诺数较高,飞行马赫数较高,翼面上具有60%~70%弦长的维持自然层流所需的有一定顺压梯度压力分布形态是不现实的,因此在基本翼型设计时,下翼面压力分布顺压范围定在50%左右,上翼面45%左右,以弱激波结束上翼面压力分布顺压形态,如图4所示(图中Cp为压力系数,c为参考弦长,x为弦向坐标);翼型具有适度的后加载,有利于减小低头力矩,保证翼型后部的厚度。
整个机翼由4个翼型控制剖面进行三维构造,翼根、拐折、70%展长位置和翼梢4个设计翼型。因机翼当地雷诺数内翼大,外翼小,内翼剖面最大厚度位置相对基本翼型前移,外翼后移,内翼上翼面顺压梯度相对弦长范围减小,外翼增加。内翼相对厚度大,外翼相对厚度小,外翼相对内翼几何负扭转,与一般机翼设计规律一致。最终设计所得4个剖面翼型如图5所示,y为垂直于弦向的坐标,η为展向位置与展长的比值。最终所得展向相对厚度分布及扭转角分布如图6所示,其中T为厚度。

图4 基本翼型设计状态压力系数分布Fig.4 Distributions of base airfoil pressure coefficients on design point
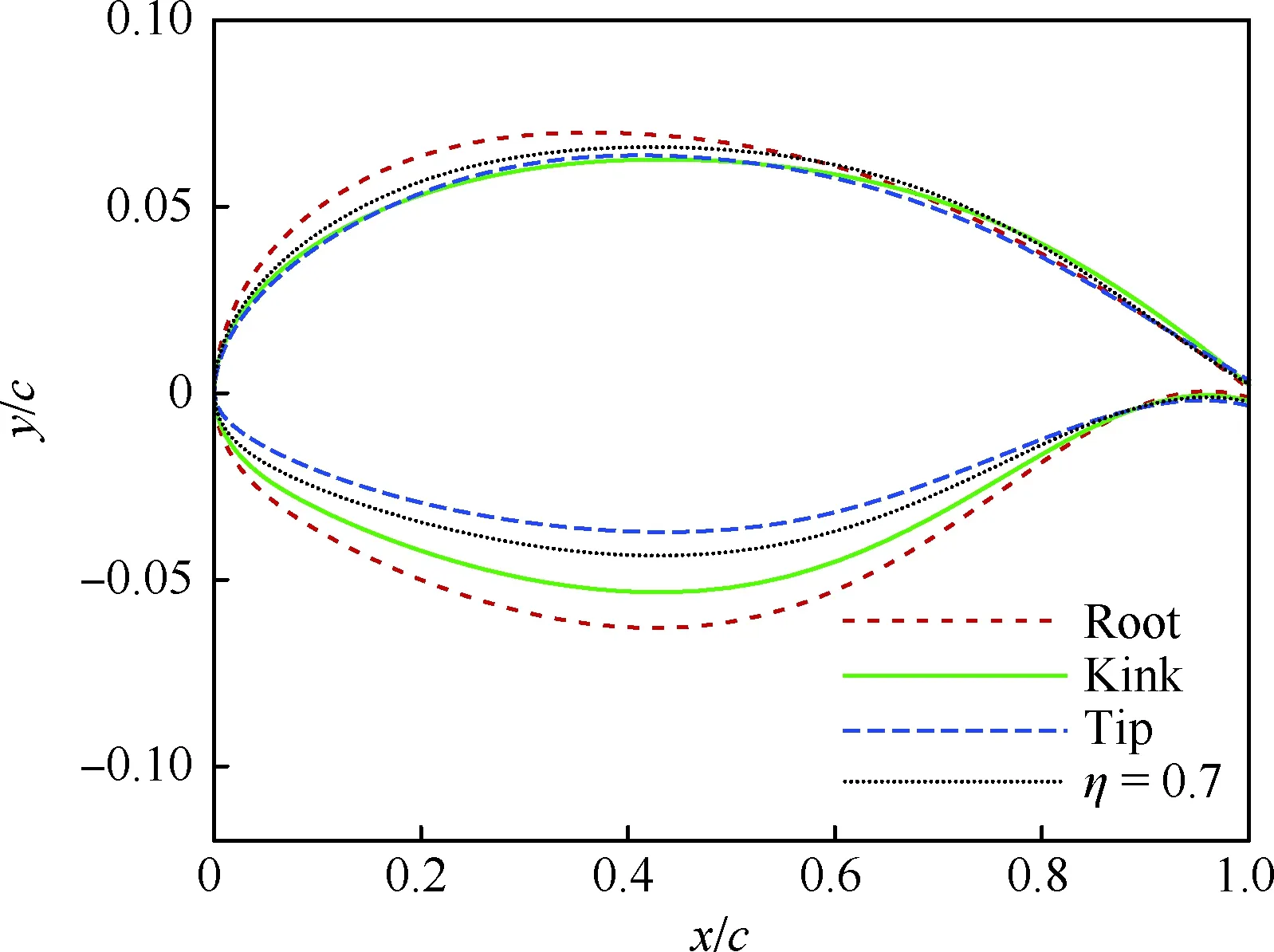
图5 机翼翼根、拐折、η=0.7处和翼梢的翼型Fig.5 Airfoils at root, kink, η=0.7 and tip of wing

图6 展向相对厚度分布和扭转角分布Fig.6 Distribution of relative thickness and twist angle in spanwise direction
1.2 边界层转捩预测方法
包络法中求解扰动放大因子时,n可以定义为
(1)
式中:s0和s分别表示沿流向积分的起始点和当前位置;n的值取决于当地边界层形状因子以及动量损失厚度雷诺数Reθ,如果当地边界层形状因子以及动量厚度能够合理地进行当地化,流场中任意一点扰动因子的当地增长就可以求出。Coder和Maughmer[27]通过分析边界层相似性解,构建了合理的计算当地形状因子的公式,使用输运方程对放大因子进行求解:
(2)
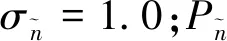
(3)
式中:σf=1.0;Pγ和Eγ分别为产生源项和破坏源项;间歇因子γ与Menterk-ω剪切应力输运(SST)湍流模式的耦合方式和各源项的详细计算公式见文献[27]。关于该方法的可靠性校核验证见文献[27-28],本文不再赘述。
1.3 气动特性评估
CFD求解过程中,采用格心格式有限体积法求解可压缩Navier-Stokes方程,无黏通量通过Roe的通量差分分裂FDS(Flux Difference Splitting)格式求解,黏性通量采用中心差分格式进行离散,时间推进采用近似因子分解(Approximate Factorization)方法。使用多重网格和网格序列技术加速求解的收敛。程序通过基于MPI(Message Passing Interface)的分布式并行策略提高计算速度。
数值模拟采用的网格分布如图7所示。气动特性分析分别使用自由转捩和全湍流计算,在马赫数为0.75、雷诺数为1×107的工况下,图8给出了计算所得升阻力系数极曲线,CL为升力系数,CD为阻力系数。自然层流设计带来的减阻效果非常明显,翼身组合体的阻力减小在30 counts(1 count=1.0×10-4)左右,如果加上层流短舱等的贡献,减阻量将更加可观,由此可见自然层流设计的巨大潜力和可观收益。

图7 计算网格分布Fig.7 Distribution of computational mesh
图9给出了自由转捩和全湍流工况下的翼身组合体构型的阻力发散曲线,分别评估了定升力系数0.38、0.42和0.46 3个升力状态。无论全湍流还是自由转捩工况,Ma=0.77与设计点Ma=0.75阻力系数变化不超过20 counts,满足马赫数增加0.02、阻力系数增加不超过20 counts的要求,因而阻力发散特性良好。
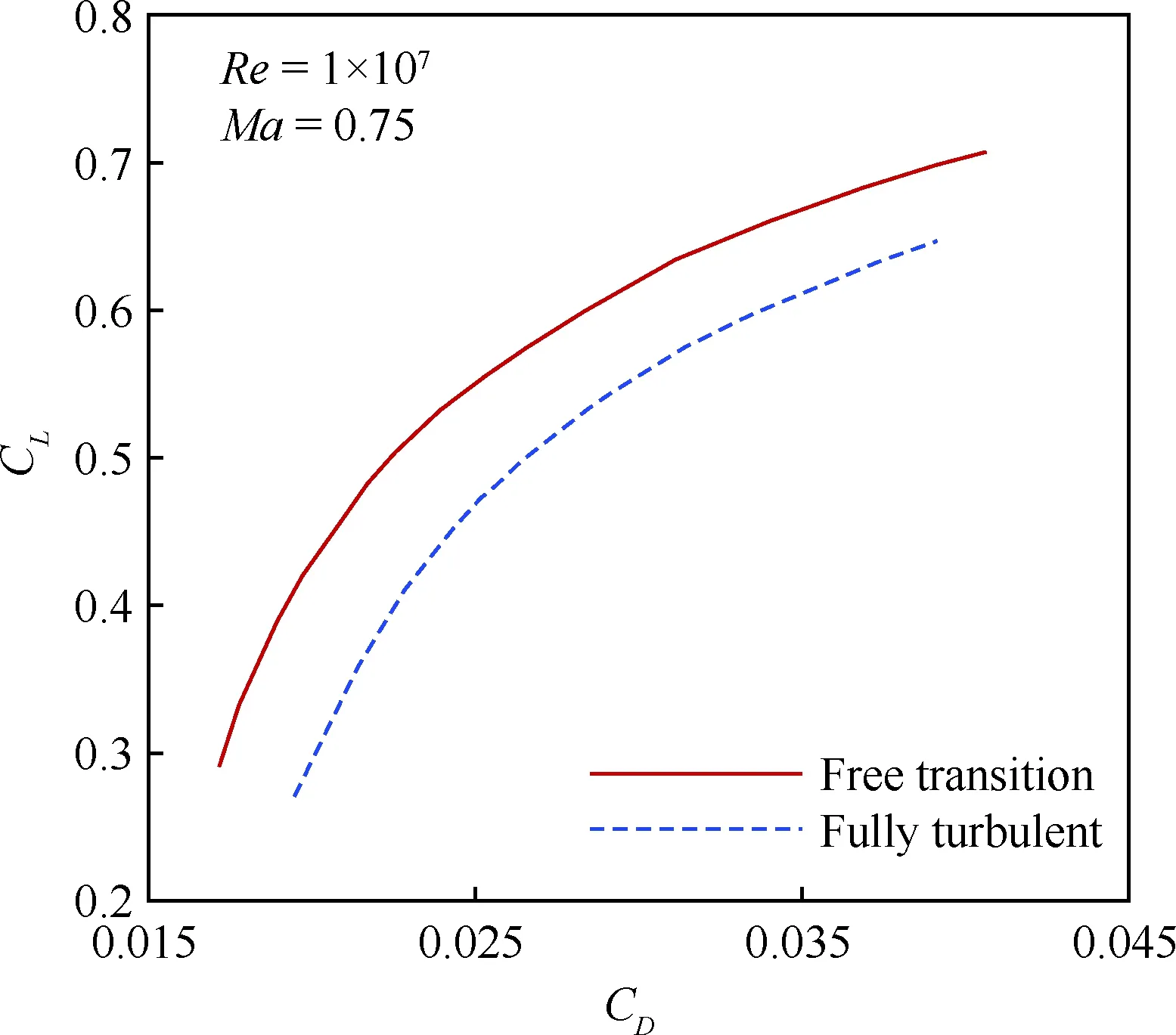
图8 自由转捩和全湍流工况下翼身组合体的 升阻力系数极曲线Fig.8 Curves between lift coefficient and drag coefficient at the free transition and fully turbulent condition

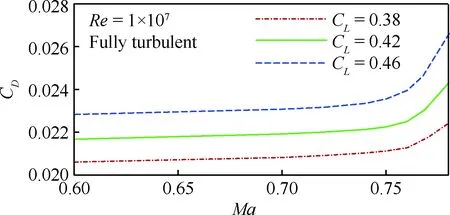
图9 自由转捩和全湍流工况下翼身组合体的 阻力发散曲线Fig.9 Curves of drag divergence between lift coefficient and drag coefficient at the free transition and fully turbulent condition
下面将详细评估该机翼在设计点附近的压力分布和边界层转捩特性。
首先,在设计点附近进行了马赫数扰动变化的压力分布分析,定升力系数为0.42,Ma=0.74, 0.75,0.76,计算所得不同展向位置的压力分布对比如图10所示。由图可知,马赫数的小幅度变化对机翼几乎所有展向位置的压力分布均有较为明显的影响,尤其是上表面,其主要是由于激波位置的前后移动所致,马赫数越大,激波位置越靠后,下表面则变化幅度非常小。
然后,图11给出了Ma=0.75,CL=0.38,0.42 ,0.46时,计算所得不同展向位置的压力分布对比。由图可知,不同升力系数直接影响的是飞行迎角,与马赫数变化产生的效应类似,不同升力系数下的压力分布差异主要集中在上表面激波位置附近,升力系数越大,对应迎角越大,激波位置后移,但是后移程度不及马赫数变化产生的偏移量。同样地,下表面压力分布受影响很微弱。
最后,在设计点(Re=1×107,Ma=0.75,CL=0.42)状态,机翼上下表面摩擦力系数Cf分布如图12所示。分析云图可知,除了机翼和机身结合部的干扰所致转捩,其余部分均与压力分布形态对应良好。从内翼段到外翼段,上下表面的转捩位置均出现在逆压梯度出现的压力恢复区域,尤其是上表面在激波出现的位置附近,该状态下并无激波诱导附面层分离泡转捩出现。这也与设计的目标一致:即在顺压梯度保证TS波的抑制发展,逆压梯度区TS波则会快速增长,诱发转捩,由此获得层流设计。
经过精细的气动设计和高精度CFD验证之后,将设计构型加工成风洞试验模型,进行风洞试验验证。关于该机翼其他工况下的转捩特性分析和验证将在后续章节与风洞试验结果一起进行。
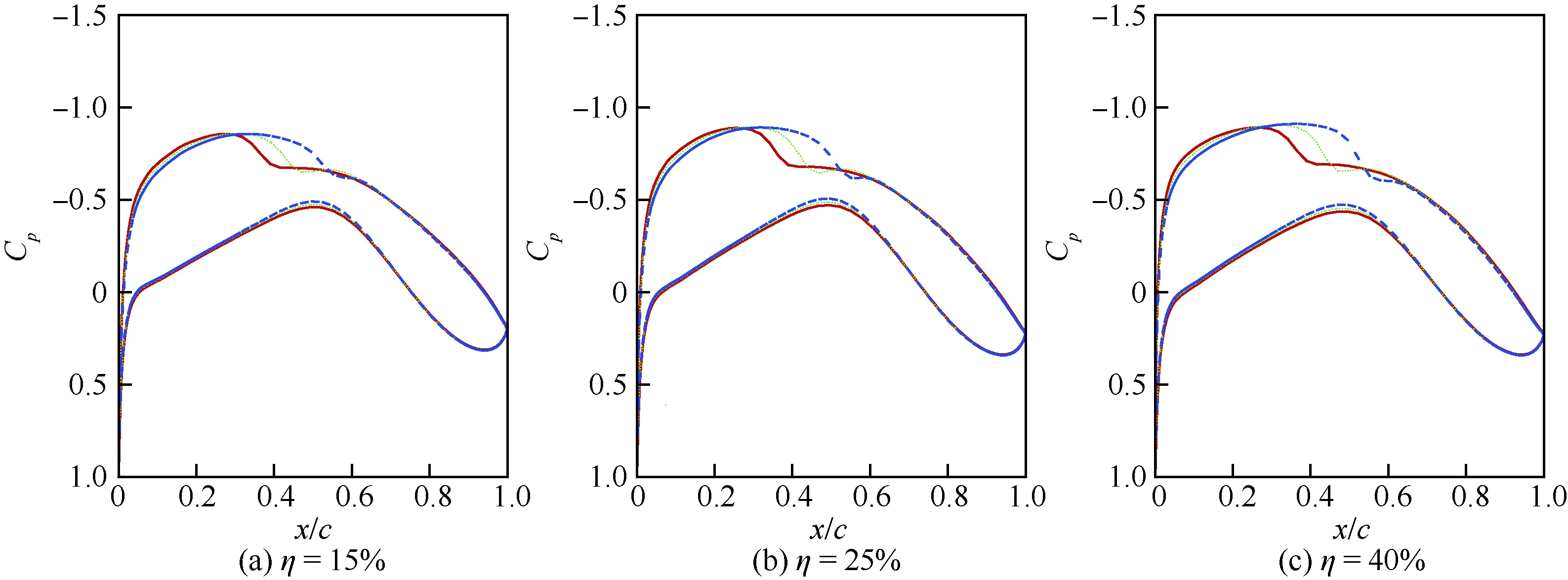
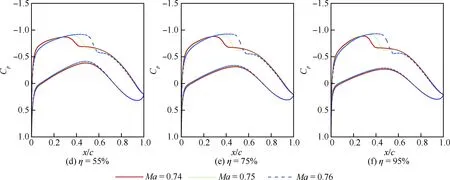
图10 Ma=0.74,0.75,0.76时机翼不同展向位置的压力系数分布对比Fig.10 Comparison of pressure coefficient distribution at different spanwise sections of wing at Ma =0.74, 0.75, 0.76


图11 CL=0.38, 0.42, 0.46时机翼不同展向位置的压力系数分布对比Fig.11 Comparison of pressure coefficient distribution at different spanwise sections of wing at CL=0.38, 0.42, 0.46

图12 设计点机翼表面摩擦力系数云图(Re=1×107,Ma=0.75,CL=0.42)Fig.12 Contour of skin friction coefficient on the wing surface at design point (Re=1×107, Ma=0.75, CL=0.42)
2 风洞试验设施和测量技术
2.1 荷兰HST风洞和模型加工情况
风洞试验在荷兰阿姆斯特丹的DNW(German-Dutch Wind tunnels)风洞群内的HST(High Speed wind Tunnel)跨声速风洞进行[34-35]。需要指出的是,HST风洞自1950年前后建成运营以来,进行了各种各样的民机和军机的风洞试验,取得了非常高的试验数据精度和风洞品质。该风洞的宏观构造图如图13所示,它是一款可变密度的回流式风洞,风洞滞止压强范围为20~390 kPa,风洞试验段尺寸1.8 m×2.0 m,马赫数覆盖范围为0.1~1.3,雷诺数上限可达1×107,流场品质较高,尤其适合高雷诺数跨声速风洞试验。
风洞试验模型首先按照表2中的详细参数对设计构型进行了1∶10.4的三维等比例缩放,精密加工之后,接着对设计构型使用结构有限元进行了强度和刚度校核,计算出安全系数满足HST风洞要求。机翼外露部分表面粗糙度为Ra=0.4 μm, 机身外露部分表面粗糙度为Ra=0.8 μm,其余部分粗糙度为Ra=1.6 μm。因为是半模试验,所以需在机身与风洞洞壁之间添加附面层隔板,外置天平进行测力,翼身组合体试验构型在风洞试验段的安装情况如图14所示。

图13 DNW-HST跨声速风洞Fig.13 DNW-HST transonic wind tunnel
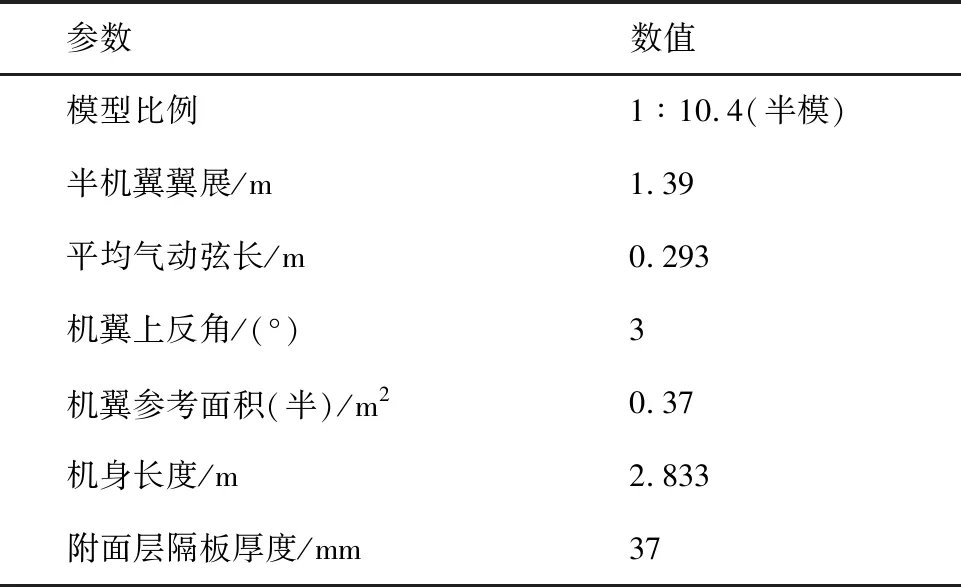
表2 风洞试验翼身组合体具体参数
图14 风洞试验段中翼身组合体构型的 半模试验构型Fig.14 Overview of wing-body combination half-model in wind tunnel test section
2.2 TSP技术和测量细节
TSP技术主要利用光学技术实现风洞模型表面温度的测量[36]。具体操作为:首先将温敏材料均匀涂于机翼表面,确保气动外形不受影响。然后打开风洞制冷装置,对风洞的气流和风洞试验机翼进行冷却。准备进行转捩测量时,关闭制冷装置,此时吹入风洞的气流温度相比于物面温度较高,在机翼表面将会进行较为强烈的热传递现象。湍流边界层的热传导效率较高,而层流边界层则较低,因此会在机翼表面出现明显的温度差,通过光学技术对物面温度进行拍照识别,从而判定层流-湍流区域。
TSP涂层厚度为150~200 μm,3个标志带,展向25%、55%和85%展长处,每10%弦长一个标志点。此外,转捩带位于距离前缘7%弦长处,如图15 所示。测压孔径在机翼表面为∅=0.2 mm,保证测压孔轴线与当地型面法线方向一致,偏差小于3′。测压孔周围没有毛刺、杂质、倒角和凹凸不平。测压管选取外径1.0 mm,内径0.7 mm的不锈钢管,使用前按照要求会进行气密性检查。测压孔布置在展向35%和49%展长处,如图16所示。每个剖面上下表面各12个测压孔,监测10%~80%弦长区间内的离散压力分布。

图15 流向等间距标志孔和固定转捩带布置Fig.15 Uniformly spaced marked holes in streamwise direction and distribution of fixed transition tripping dots
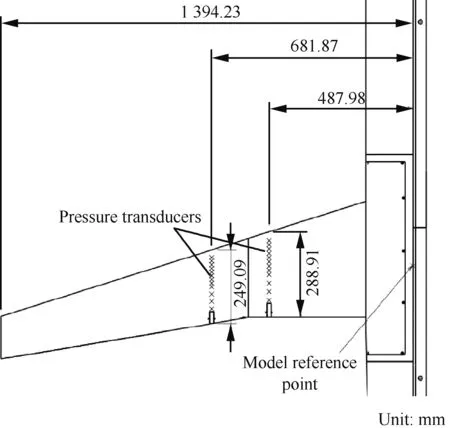
图16 两个测压剖面的位置Fig.16 Overview of two cross-sections with pressure taps
3 风洞试验结果和数值模拟分析
风洞试验全部试验工况涵盖了:马赫数Ma=0.70,0.75,0.78,0.80,雷诺数Re=6×106,8×106, 9×106,10×106,迎角为1°和2°。但是随着风洞试验的进行,有很多工况下的转捩测量由于气流污染物、物面污染物等因素的影响导致测量不是非常稳定。表3给出了最终风洞试验结果中流场品质和转捩测量效果均处于高水平高质量的试验工况。下文将结合风洞试验结果和数值模拟结果,详细探讨和研究这些变化的参数对跨声速自然层流机翼在设计点附近的边界层转捩特性的影响。
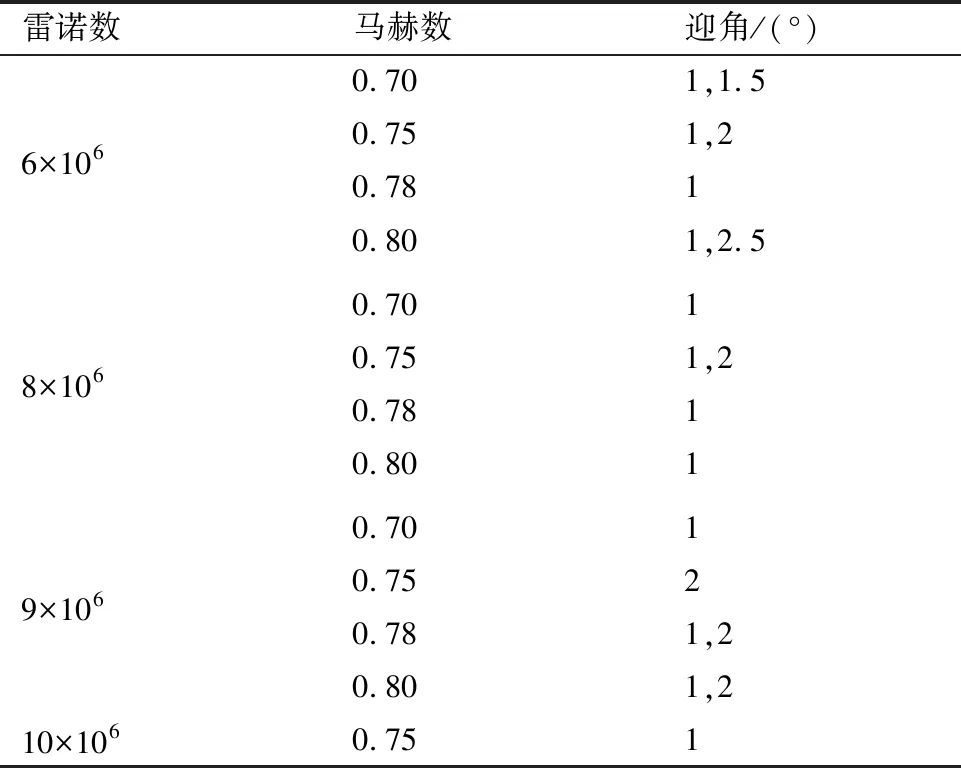
表3 风洞试验高质量测量工况
3.1 同状态不同车次试验结果
首先对风洞试验结果的重复性试验精度进行了验证,图17展示了Ma=0.75、Re=6×106、迎角α=2°工况下,不同车次的转捩分布。由内外翼段的转捩线分布可知,虽然后续车次物面被些许污染物污染,但是整体转捩位置变化非常小,证实了测量试验的高精度和合理性。
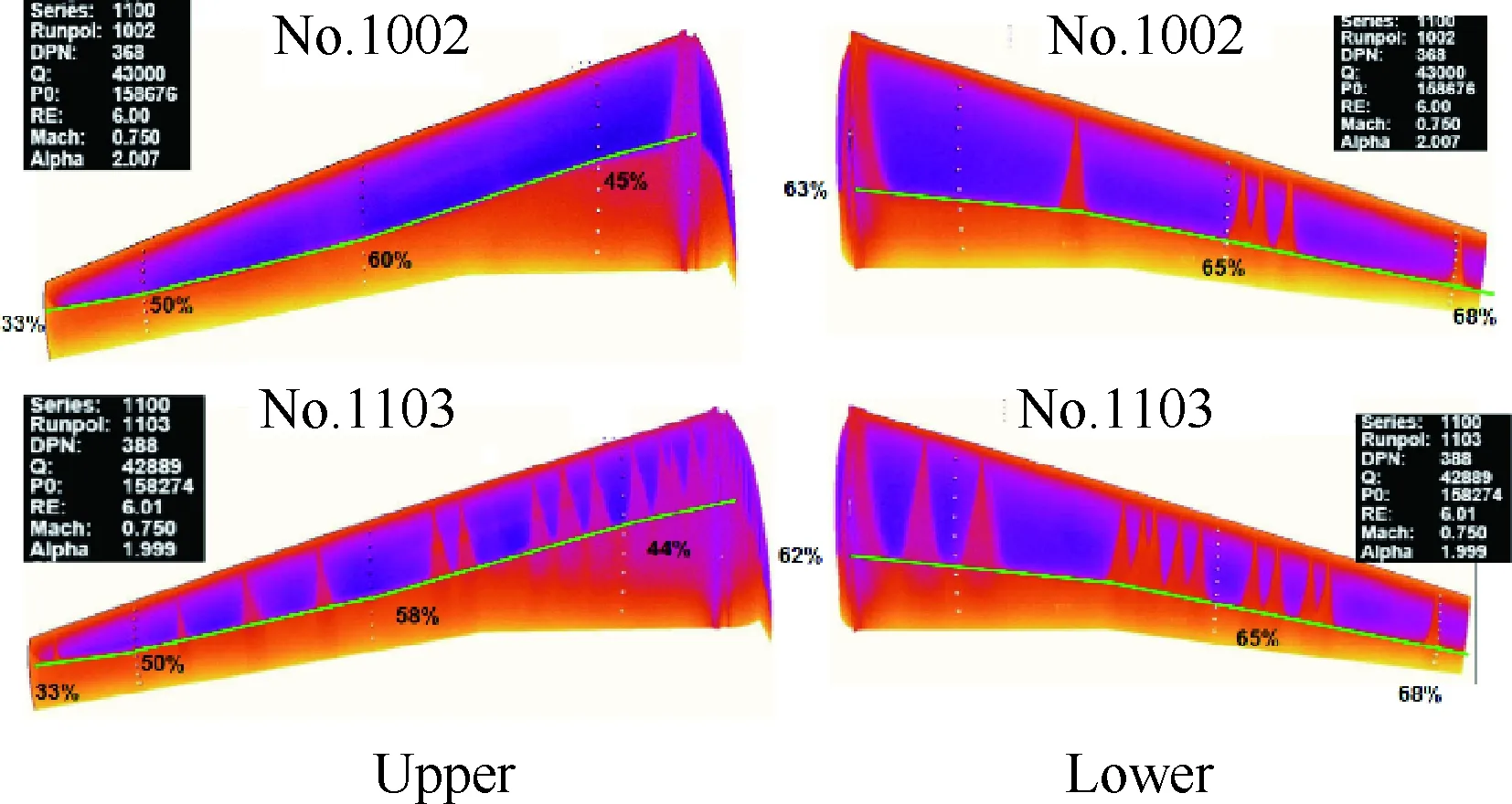
图17 不同车次的TSP测量所得机翼 表面层流-湍流区域分布Fig.17 Distribution of laminar-turbulent region on wing surface measured by TSP technique at different test numbers
3.2 变马赫数分析
雷诺数Re=8×106、迎角α=1°,4个试验马赫数Ma=0.70,0.75,0.78,0.80工况下的TSP技术拍摄层流-湍流分布如图18所示。由试验结果可知,设计雷诺数和迎角1°固定,马赫数从0.70 逐渐增大到0.80,机翼下表面的层流范围几乎不变,而上表面的边界层转捩特性则会经历一个比较复杂的变化过程。马赫数从0.70增大到0.75时,上表面外翼段层流区缩短,内翼段略有增长。马赫数继续增大到0.78和0.80,上翼面的层流区都急剧增加,且马赫数0.78和 0.80 工况下的上表面层流区范围差异很小。
为了分析其转捩特性变化的原因,本文对试验构型进行了高精度转捩数值模拟,如图19所示。截取不同马赫数下机翼上表面和下表面的典型展向位置的压力分布,对比分析可知在机翼下表面,随着马赫数逐渐增大,压力分布形态变化很微弱,逆压梯度起始点略有前移,因此转捩位置略微前移,转捩形式均为TS波急剧失稳产生的自然转捩。在机翼上表面,马赫数为0.70时,机翼上表面还未有明显激波出现,转捩发生于弱逆压梯度的发展过程中,TS波逐渐失稳形成自然转捩;马赫数为0.75时,机翼上表面形成较为明显的激波,转捩也发生在较强逆压梯度的激波形成区域,转捩形式依然为自然转捩;马赫数为0.78时,转捩模式受机翼的影响,在内翼段预测所得转捩位置略微靠前,在展向中部和外部区域转捩位置预测均与试验数据吻合较好。该工况下明显的特征就是在马赫数为0.78时,机翼上表面顺压梯度区非常长,可以达到75%左右,因此上表面层流区显著增长。由此带来的缺点是过长的较强顺压会形成很强的压力恢复导致强激波诱导附面层分离,因此该工况下机翼上表面出现了激波诱导附面层分离引起的转捩。

图18 TSP测量所得不同马赫数下 机翼表面层流-湍流分布Fig.18 Distribution of laminar-turbulent region on wing surface measured by TSP technique at different Mach numbers

图19 转捩计算所得不同马赫数下机翼 表面层流-湍流分布Fig.19 Distribution of laminar-turbulent region on wing surface measured by transition calculations at different Mach numbers
3.3 变雷诺数分析
马赫数Ma=0.75、飞行迎角α=1°、3个试验雷诺数Re=6×106,8×106,10×106工况下的TSP技术拍摄层流-湍流分布如图20所示。由图可知,随着雷诺数的增加,机翼上下表面转捩位置随着雷诺数的增加略微前移,但是变化幅度非常小。图21给出了6×106、8×106和10×1063个雷诺数工况下机翼上下表面的转捩数值模拟结果。由压力分布形态可知,随着雷诺数的增加,激波位置受到细微的影响,但幅度很小,机翼上表面转捩位置整体随着雷诺数增加略微前移,而下表面转捩位置则与逆压梯度起始点一致,并未随着雷诺数增加而明显变化。

图20 TSP测量所得不同雷诺数下机翼 表面层流-湍流分布(α=1°)Fig.20 Distribution of laminar-turbulent region on wing surface measured by TSP technique at different Reynolds numbers (α=1°)
马赫数Ma=0.75,飞行迎角α=2°,3个试验雷诺数Re=6×106,8×106,9×106工况下的TSP技术拍摄层流-湍流分布如图22所示。由图可知,随着雷诺数的变化,机翼上下表面转捩位置依然变化非常微弱。
图23给出了6×106、8×106和9×1063个雷诺数工况下机翼上下表面的转捩数值模拟结果。截取内中外翼3个典型展向位置的压力分布,可见在该跨声速状态下,机翼上下表面的压力分布和激波形态随着雷诺数的增加变化微小,下表面的转捩预测位置与试验数据吻合良好,均发生在逆压梯度起始位置;在上表面,转捩模式预测的内翼段转捩位置会随着雷诺数的增加有些许前移,计算所得TS波在接近但还未抵达激波位置时就发生了转捩,但试验结果显示在内翼段的层流区并未受到雷诺数的影响。而在机翼的中部和外部,数值模拟所得转捩位置均与激波起始位置和试验测量数据保持一致。但是在2°迎角工况下,机翼上表面中外翼段的强激波将会诱导附面层分离触发转捩。这种激波诱导附面层分离现象在Re=6×106时最为明显,随着雷诺数的增加,分离泡现象会逐渐减弱。

图21 转捩计算所得不同雷诺数下机翼 表面层流-湍流分布(α=1°)Fig.21 Distribution of laminar-turbulent region on wing surface measured by transition calculations at different Reynolds numbers (α=1°)

图22 TSP测量所得不同雷诺数下机翼 表面层流-湍流分布(α=2°)Fig.22 Distribution of laminar-turbulent region on wing surface measured by TSP technique at different Reynolds numbers (α=2°)
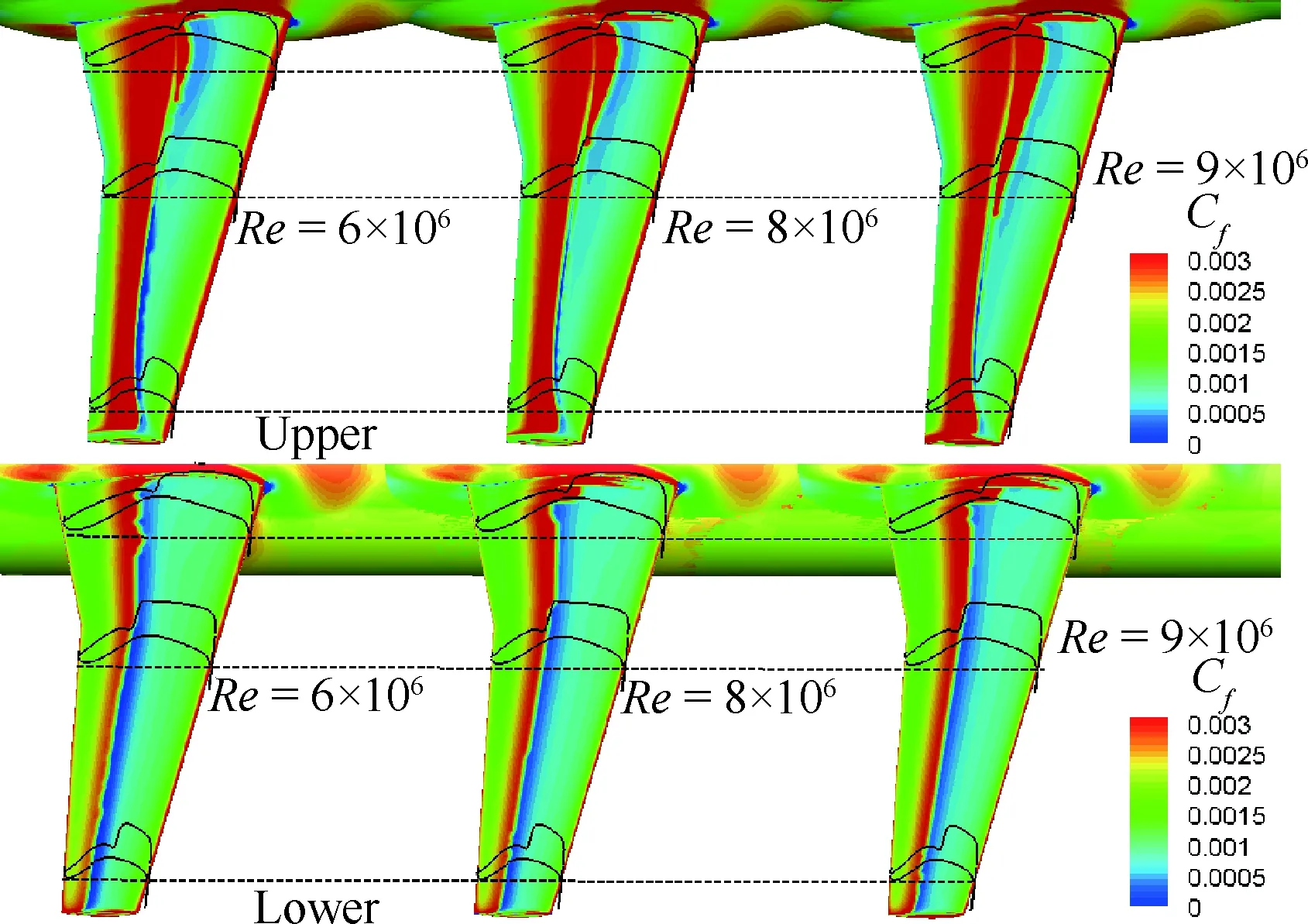
图23 转捩计算所得不同雷诺数下机翼 表面层流-湍流分布(α=2°)Fig.23 Distribution of laminar-turbulent region on wing surface measured by transition calculations at different Reynolds numbers (α=2°)
在试验中展向35%和49%展长位置处的测压探针所测得压力分布数据与CFD数值模拟的结果对比如图24所示。由图可知,无论转捩预测还是试验数据均显示该工况下压力分布对雷诺数变化并不敏感。顺压梯度的保持使得层流区域得以维系,随着强激波的出现,会产生激波诱导附面层分离现象,从而触发转捩。
3.4 变迎角分析
马赫数Ma=0.75,飞行雷诺数Re=8×106,2个飞行迎角α=1°、α=2°工况下的TSP技术拍摄层流-湍流分布如图25所示。由图可知,迎角由1°增加到2°,机翼上表面层流区域有所增长,而下表面则变化非常小。与之对应的转捩数值模拟结果如图26所示,由图可知迎角变化最明显的影响就是激波位置和强度。迎角由1°增加到2°时,机翼下表面压力分布形态非常接近,转捩位置也变化很小;机翼上表面激波位置后移,层流区也随之增长,但中外翼段转捩形态由自然转捩变为强激波诱导附面层分离泡转捩。

图24 转捩计算所得不同雷诺数下机翼表面压力系数分布与试验数据的对比(α=2°,Ma=0.75)Fig.24 Comparison of pressure coefficient distribution on wing surface between transition calculations and measured data at different Reynolds numbers (α=2°,Ma=0.75)
本文重点关注超临界层流机翼的边界层转捩特性,对于阻力测力结果则只做定性说明。风洞半模测力试验误差比较大,因此阻力系数的绝对数值分析价值不高。但是其所反应的趋势,与CFD数值模拟一致:以固定转捩为例(转捩带位于距离前缘7%弦长位置处),马赫数Ma=0.75, 迎角α=1°,雷诺数从6×106增加到10×106,翼身组合体的阻力以近似线性的关系在减小。分析其原因在于随着雷诺数的增加,翼身组合体的当量厚度(实际厚度+附面层厚度)减小,压差阻力减小,其中摩擦阻力的减小量非常小。

图25 TSP测量所得不同迎角下机翼 表面层流-湍流分布Fig.25 Distribution of laminar-turbulent region on wing surface measured by TSP technique at different angles of attack

图26 转捩计算所得不同迎角下机翼 表面层流-湍流分布Fig.26 Distribution of laminar-turbulent region on wing surface measured by transition calculations at different angles of attack
4 结 论
通过超临界自然层流机翼的气动设计和风洞试验,以及转捩数值模拟情况进行详细的介绍和对比分析,本文对于超临界自然层流机翼的边界层特性和设计理念得出以下几点结论:
1) 对于超临界自然层流机翼,在一定范围内(雷诺数<1×107,升力系数<0.5),雷诺数的增加会使转捩位置略微前移,但雷诺数并不是主导自然转捩的关键因素;其他因素不变,在一定范围内(雷诺数<1×107,升力系数<0.5),雷诺数增加,飞行器总阻力减小。
2) 对于超临界自然层流机翼,在1×107雷诺数量级,马赫数和飞行迎角是主导边界层转捩的主导因素,因为这2个因素将直接影响压力分布形态,能够改变顺压梯度区和激波位置以及强度,从而决定转捩位置和转捩类型。顺压梯度区过长,则层流区域增加,但会形成强激波诱导附面层分离泡转捩;顺压梯度区过短,则层流区域缩短,自然转捩会在弱逆压梯度区域形成。
3) 基于扰动放大因子的转捩模式对本文构型的转捩预测基本与试验数据吻合良好,为超临界自然翼型和机翼的设计提供了可靠的计算分析工具。
4) 对于20°以下的后掠角,1×107量级的超临界自然层流机翼的设计规律就是对于顺压梯度的设计必须和激波位置匹配,过强的顺压梯度会导致强激波诱导附面层分离,过弱的顺压梯度则很难维持充足的层流区域。对更大后掠、更高雷诺数的机翼需要考虑横流不稳定性转捩的影响,需要直接进行三维稳定性分析、三维气动设计以及流动控制。
5) 在流场品质不佳的环境下,机翼表面非常容易被污染,层流很难维持;随着时间的推进,层流区域将会被污染物强制转捩成湍流。因此,层流设计的发展需要突破工业加工精度和如何保持机翼表面光洁等技术难题。
6) 该试验模型可以作为边界层转捩研究者的验证模型,其包含跨声速可压缩边界层高雷诺数工况的TS波和激波诱导附面层转捩现象。

